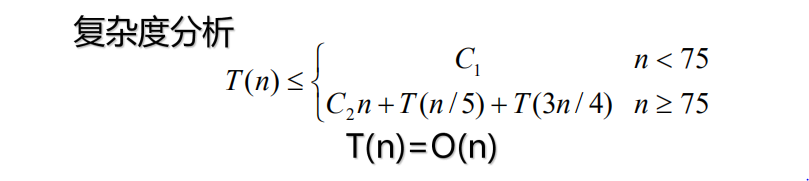递归与分治策略_分治策略将求出的小规模的问题的解合并为一个更大规模的问题的解,自顶向下逐步求

递归与分治策略

• 将问题分解为k个子问题，对这k个子问题分别求解。
• 如果子问题的规模仍然不够小，则再划分为k个子问题，如此递归的进行下去，直到问题的规模足够小，很容易求出其解为止。
• 将求出的小规模的问题的解合并为一个更大规模的问题的解，自底向上逐步求出原来问题的解。
  

（★）递归的概念

• 直接或间接地调用自身地算法称为递归算法。用函数自身给出定义的函数称为递归函数。
• 由分治法产生的子问题往往是原问题的较小模式，这就为使用递归技术提供了方便。在这种情况下，反复应用分治手段，可以使子问题与原问题类型一致而其规模却不断缩小，最终使子问题缩小到很容易直接求出其解。这自然导致递归过程的产生。
• 分治与递归像一对孪生兄弟，经常同时应用在算法设计之中，并由此产生许多高效算法。

1. 阶乘函数

// 阶乘函数 
int factorial(int x)
{
	if(x == 0)
		return 1;
	return x*factorial(x-1);
}
1
2
3
4
5
6
7

2. Fibonacci数列

// Fibonacci数列 
int fibonacci(int x)
{
	if(x<=1)
		return 1;
	return fibonacci(x-1) + fibonacci(x-2);
}
1
2
3
4
5
6
7

3. Ackerman函数

4. 全排列问题

// 全排列问题
int permutation(int *arr, int pos, int n)
{
	// 边界条件 
	if(pos == n)  
	{
		print_arr(arr, n);
		return 0;
	}
		
	for(int i=pos, i<n; i++)
	{
		swap(arr, i, pos);
		permutation(arr, pos+1, n);
		swap(arr, i, pos);
	}
	return 0;	
} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

5. 整数划分问题

将整数n表示成一系列正整数之和

在本题中，如果设p(n)为正整数n的划分数，则难以找到递归关系，因此考虑增加一个自变量：
将n最大加数不大于m的划分数个数记为q(n,m)
可以建立q(n,m)的如下递归关系

• q(n,1) = 1, n>=1;
  当最大加数$n_i$不大于1时，任何正整数n只有一种划分形式，即n=1+1+1+…+1
• q(n,m) = q(n,n), 当m>=n;
  最大加数$n_i$实际上不能大于n。
  因此，q(1,m) = 1
• q(n,n) = 1+ q(n,n-1);
  正整数n的划分由$n_i$ = n的划分和$n_i$ <=n-1的划分组成
• q(n,m) = q(n,m-1) + q(n-m,m), n>m>1;
  正整数n的最大加数$n_i$ 不大于m的划分由：
  $n_i$ <=m-1的划分（全部划分<M）和$n_i$ = m的划分组成
  

6. Hanoi塔问题

将A上n-1个圆盘移到C上，再将最后一个圆盘移到B上，最后将C上n-1个圆盘移到B上。

void hanoi(int n, int a, int b, int c)
{
	hanoi(n-1, a, c, b);
	move(a, b);
	hanoi(n-1, c, b, a);
 } 
1
2
3
4
5
6

分治法的基本思想

分治法所能解决的问题一般具有以下几个特征：

• 该问题的规模缩小到一定的程度就可以容易的解决；
• 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质
• 利用该问题分解出的子问题的解可以合并为该问题的解；
• 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题
  这条特征涉及到分治法的效率，如果各个子问题是不独立的，则分治法要做许多不必要的工作，重复地解公共的子问题，此时虽然也可用分治法，但一般用动态规划较好。

divide-and-conquer(p)
{
	if(|p| <= n0) adhoc(p);  // 解决小规模问题
	divide p into smaller subinstances p1,p2,...pk;  // 分解问题
	for(i=0; i<=k; i++)  // 参考全排列子问题 
		yi = divide-and-conquer(pi);  // 递归的解各子问题
	return merge(y1,...,yk);  // 将各子问题的解合并为原问题的解 
 } 
1
2
3
4
5
6
7
8

在用分治法设计算法时，最好使子问题的规模大致相同。即将一个问题分成大小相等的k个子问题的处理方法是行之有效的。这种使子问题规模大致相等的做法是出自一种平衡子问题的思想，它几乎总是比子问题规模不等的做法要好。

一个分治法将规模为n的问题分成k个规模为n/m的子问题去解。设分解阈值n0=1 ,且adhoc解规模为1的问题耗费1个单位时间。再设将原问题分解为k个子问题以及用merge将k个子问题的解合并为原问题的解需要f(n)个单位时间。则T(n)表示该分治法解规模为|p| = n的问题所需的计算时间，则有：

二分搜索技术

template<class Type>
int BinarySearch(Type a[], const Type& x, int n)
{	
	int left = 0, right = n-1;
	//找到x返回其在数组中的位置，否则返回-1 
	while(left <= right)
	{
		int middle = (left + right) / 2;
		if(x == a[middle]) return middle;
		if(x > a[middle]) left = middle + 1;
		else
			right = middle - 1;
	}
	return -1;  // 未找到x 
} 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

大整数的乘法

Strassen矩阵乘法

（★）棋盘覆盖

// tr, tc:棋盘左上角行坐标，列坐标
// dr, dc:特殊方格的行坐标，列坐标
// size: 棋盘的行/列数 
void ChessBoard(int tr, int tc, int dr, int dc, int size)
{
	if(size == 1) 
		return;
	int t = tile++,  // L型骨牌号
	s = size / 2; 
	
	if(dr<tr+s && dc<tc+s)  // 特殊方格在左上角棋盘 
		ChessBoard(tr, tc, dr, dc, s);
	else  // 左上角棋盘没有特殊方格 
	{
		// 用t号L型骨牌覆盖右下角 
		Board[tr+s-1][tc+s-1] = t;
		// 覆盖其余方格 
		ChessBoard(tr, tc, tr+s-1, tc+s-1, s); 
	}
	
	if(dr<tr+s && dc>=tc+s) // 特殊方格在右上角棋盘
		ChessBoard(tr, tc+s, dr, dc, s)
	else
	{
		Board[tr+s-1][tc+s] = t;
		ChessBoard(tr, tc+s, tr+s-1, tc+s, s);
	 }
	 
	 if(dr>=tr+s && dc<tc+s)  // 特殊方格在左下棋盘
	 	ChessBoard(tr+s, tc, dr, dc);
	else
	{
		Board[tr+s][tc+s-1] = t;
		ChessBoard(tr+s, tc, tr+s, tc+s-1, s);
	 } 
	 
	if(dr>=tr+s && dc>=tc+s)  // 特殊方格在右下棋盘
		ChessBoard(tr+s, tc+s, dr, dc, s);
	else
	{
		Board[tr+s][tc+s] = t;
		ChessBoard(tr+s, tc+s, tr+s, tc+s, s);
	 } 	
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

（★）合并排序

template<class Type>
//递归方法
void MergeSort(Type a[], int left, int right)
{
	if(left<right)
	{
		int i = (left+right)/2;
		MergeSort(a, left, i);
		MergeSort(a, i+1, right);
		Merge(a, b, left, i, right);  // 合并到数组b 
		Copy(a, b, left, right);  // 复制回数组a 
	}
 } 

template<class Type>
// 合并c[l:m]和c[m+1:r]到d[l:r] 
void Merge(Type c[], Type d[], int l, int m, int r)
{
	int i = l, j = m+1, k = l;
	while(i<=m && j<=r)
		if(c[i]<=c[j]) 
			d[k++] = c[i++];
		else
			d[k++] = c[j++];
	if(i>m)
		for(int q=j, q<=r; q++)
			d[k++] = c[q];
	else
		for(int q=i; q<=m; q++)
	 		d[k++] = c[q];  
 } 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

（★）快速排序

template<class Type>
void MergeSort(Type a[], int p, int r)
{
	if(p<r)
	{
		int q = Partition(a, p, r);
		MergeSort(a, p, q-1);
		MergeSort(a, q, r);	
	} 

}

// 以a[p]为基准，小于的交换到左边区域，大于的交换到右边区域 
template<class Type>
int Partition(Type a[], int p, int r)
{
	type x = a[p];
	int i = p, j = r+1;
	while(true)
	{
		while(a[++i]<x && i<r);
		while(a[--j]>x);
		if(i>=j) break;
		swap(a[i], a[j]);	
	}
	a[p] = a[j];
	a[j] = x;
	return j;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

线性时间选择

template<class Type>
Type RandomizedSelect(Type a[], int p, int r, int k)
{
	if(p==r) return a[p];
	int i = RandomizedPartition(a, p, r),
		j = i-p+1;
	if(k<=j) 
		return RandomizedSelect(a, p, i, k);
	else
		return RandomizedSelect(a, i+1, r, k-j); 
}
1
2
3
4
5
6
7
8
9
10
11

（★）循环赛日程表

void GameTable(int k, int a[][N])  // 数组下标从1开始
{
	int n = 1;
	for(int i=1; i<=k; i++)
		n *= 2;  // 求总人数
	for(int i=1; i<=n; i++)
		a[1][i] = i;  // 第一行排1-8
	int m = 1;  // 用来控制每一次填表时i行j列的起始填充位置
	for(int s=1; s<=k; s++)  // s指对称赋值的总循环次数，即分成几大步进行制作日程表
		for(int i=m+1; i<=2*m; i++)
			for(int j=m+1; j<=2*m; j++)
			{
				a[i][j+(t-1)*m*2] = a[i-m][j+(t-1)*m*2-m];  // 右下角等于左上角 
				a[i][j+(t-1)*m*2-m] = a[i-m][j+(t-1)*m*2];  // 左下角等于右上角		 
			 } 
	m *= 2; 
} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17