贪心--跳跃问题/拼接问题_跳跃问题 贪心

跳跃问题

判断能否从数轴的最左端跳跃到最右边

变形：最少跳跃次数

45.跳跃游戏

题目链接

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标。

示例 1：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
1
2
3

示例 2：

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。
1
2
3

提示：

• 1 <= nums.length <= 3 * 104
• 0 <= nums[i] <= 105

思路

维护一个当前能到达的最右端点right

遍历nums数组，不断更新right，如果right >= n-1则表示能到达终点

代码

class Solution {
    public boolean canJump(int[] nums) {
        int n = nums.length;
        int right = 0;
        //判断能否到终点
        for(int i = 0; i <= right; i++){
            right = Math.max(right,nums[i]+i);
            if(right >= n - 1) return true;
        }
        return false;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

55.跳跃游戏2

题目链接

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

• 0 <= j <= nums[i]
• i + j < n

返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
     从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。
1
2
3
4

示例 2:

输入: nums = [2,3,0,1,4]
输出: 2
1
2

提示:

• 1 <= nums.length <= 104
• 0 <= nums[i] <= 1000
• 题目保证可以到达 nums[n-1]

思路：

贪心思想，维护每个位置能到达的最右端点，当到达最右端点时跳跃次数加一，如果cur == next，则表示无法跳跃，返回-1（本题保证可以到达，所以可以省略这一步）

代码：

class Solution {
    public int jump(int[] nums) {
        int n = nums.length;
        int res = 0;
        int cur = 0; //表示当前能到达的右端点
        int next = 0; //表示下一个能到达的右端点
        for(int i = 0; i < n - 1; i++){
            next = Math.max(next,nums[i] + i);
            //当前已经到当前边界
            if(i == cur){
                cur = next;
                res++;
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

1326. 灌溉花园的最少水龙头数目

在 x 轴上有一个一维的花园。花园长度为 n，从点 0 开始，到点 n 结束。

花园里总共有 n + 1 个水龙头，分别位于 [0, 1, ..., n] 。

给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges ，其中 ranges[i] （下标从 0 开始）表示：如果打开点 i 处的水龙头，可以灌溉的区域为 [i - ranges[i], i + ranges[i]] 。

请你返回可以灌溉整个花园的 最少水龙头数目 。如果花园始终存在无法灌溉到的地方，请你返回 -1 。

示例 1：

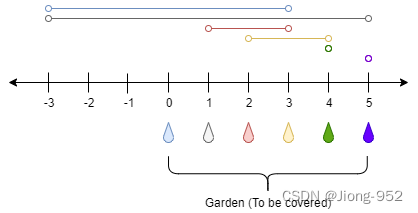
输入：n = 5, ranges = [3,4,1,1,0,0]
输出：1
解释：
点 0 处的水龙头可以灌溉区间 [-3,3]
点 1 处的水龙头可以灌溉区间 [-3,5]
点 2 处的水龙头可以灌溉区间 [1,3]
点 3 处的水龙头可以灌溉区间 [2,4]
点 4 处的水龙头可以灌溉区间 [4,4]
点 5 处的水龙头可以灌溉区间 [5,5]
只需要打开点 1 处的水龙头即可灌溉整个花园 [0,5] 。
1
2
3
4
5
6
7
8
9
10

示例 2：

输入：n = 3, ranges = [0,0,0,0]
输出：-1
解释：即使打开所有水龙头，你也无法灌溉整个花园。
1
2
3

提示：

• 1 <= n <= 104
• ranges.length == n + 1
• 0 <= ranges[i] <= 100

思路

这一题需要经过预处理，先通过题意求出right数组，表示每个位置能到达的最远右端点

代码：

class Solution {
    public int minTaps(int n, int[] ranges) {
        //求出每个位置可以到达的最远右端点
        int[] right = new int[n+1];
        for(int i = 0; i <= n; i++){
            int r = ranges[i];
            if(i > r){
                //左端点是i-r
                right[i-r] = i + r;
            }else{
                //可以覆盖0
                right[0] = Math.max(right[0],i+r);
            }
        }
        //记录跳跃次数
        int cur = 0;
        int next = 0;
        int ans = 0;
        for(int i = 0; i < n; i++){
            next = Math.max(next,right[i]);
            if(i == cur){
                //到右端点
                if(cur == next){
                    return -1;
                }else{
                    cur = next;
                    ans++;
                }
            }
        }
        return ans;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

补充练习

• 1024.视频拼接

参考代码：

注意本题的clips数据可能会超过time，需要进行过滤

class Solution {
    public int videoStitching(int[][] clips, int time) {
        int[] right = new int[time+2];
        for(int i = 0; i <= time; i++){
            right[i] = i;
        }
        Arrays.sort(clips,(o1,o2) -> o1[0] == o2[0] ? o1[1] - o2[1] : o1[0] - o2[0]);
        for(int[] cl : clips){
            int l = cl[0];
            int r = cl[1];
            if(l > time) continue;
            right[l] = Math.max(right[l],r);
        }
        int cur = 0;
        int next = 0;
        int res = 0;
        for(int i = 0 ; i < time; i++){
            next = Math.max(next,right[i]);
            if(i == cur){
                if(cur == next){
                    return -1;
                }else{
                    cur = next;
                    res++;
                }
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30