devbox
爱喝兽奶帝天荒
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

牛顿插值法——用Python进行数值计算_python写对于给定的n+1插值点,计算1到n阶差商值

作者：爱喝兽奶帝天荒 | 2024-07-09 22:16:50

赞

踩

python写对于给定的n+1插值点,计算1到n阶差商值

拉格朗日插值法的最大毛病就是每次引入一个新的插值节点，基函数都要发生变化，这在一些实际生产环境中是不合适的，有时候会不断的有新的测量数据加入插值节点集，

因此，通过寻找n个插值节点构造的的插值函数与n+1个插值节点构造的插值函数之间的关系，形成了牛顿插值法。推演牛顿插值法的方式是归纳法，也就是计算Ln（x）- Ln+1（x），并且从n=1开始不断的迭代来计算n+1时的插值函数。

 

　　牛顿插值法的公式是：

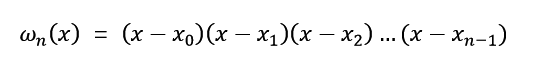
　　注意：在程序中我用W 代替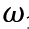 

　　计算牛顿插值函数关键是要计算差商，n阶差商的表示方式如下：

　　　　　　　　　　　　　　　　　　　　　　　　

 

　   关于差商我在这里并不讨论

　　计算n阶差商的公式是这样：

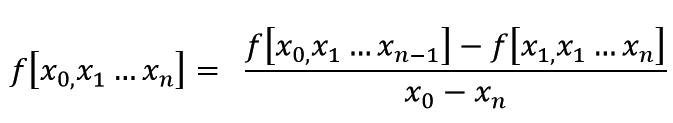
　　很明显计算n阶差商需要利用到两个n-1阶差商，这样在编程的时候很容易想到利用递归来实现计算n阶差商，不过需要注意的是递归有栈溢出的潜在危险，在计算差商的时候

更是如此，每一层递归都会包含两个递归，递归的总次数呈满二叉树分布：

　　　　

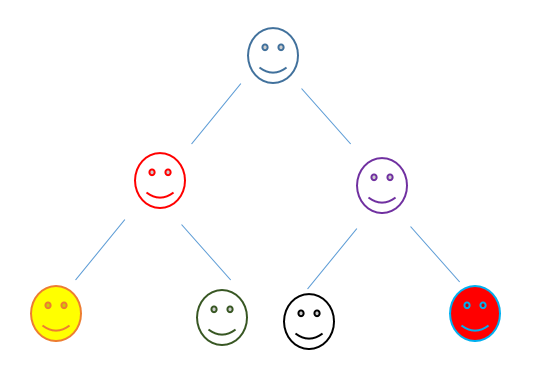
　　这意味着递归次数会急剧增加:(。所以在具体的应用中还需要根据应用来改变思路或者优化代码。

 

　　废话少说，放码过来。

　　首先写最关键的一步，也就是计算n阶差商：

1
2
3
4
5
6
7
8
9
10
11
12
13
"""
@brief:   计算n阶差商 f[x0, x1, x2 ... xn]
@param:   xi   所有插值节点的横坐标集合                                                        o
@param:   fi   所有插值节点的纵坐标集合                                                      /   \
@return:  返回xi的i阶差商(i为xi长度减1)                                                     o     o
@notice:  a. 必须确保xi与fi长度相等                                                        / \   / \
           b. 由于用到了递归，所以留意不要爆栈了.                                           o   o o   o
           c. 递归减递归(每层递归包含两个递归函数), 每层递归次数呈二次幂增长，总次数是一个满二叉树的所有节点数量(所以极易栈溢出)                                                                                    
"""
def  get_order_diff_quot(xi  =  [], fi  =  []):
     if  len (xi) >  2  and  len (fi) >  2 :
         return  (get_order_diff_quot(xi[: len (xi)  -  1 ], fi[: len (fi)  -  1 ])  -  get_order_diff_quot(xi[ 1 : len (xi)], fi[ 1 : len (fi)]))  /  float (xi[ 0 ]  -  xi[ - 1 ])
     return  (fi[ 0 ]  -  fi[ 1 ])  /  float (xi[ 0 ]  -  xi[ 1 ])

　　看上面的牛顿插值函数公式，有了差商，还差

　　这个就比较好实现了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
"""
@brief:  获得Wi(x)函数;
          Wi的含义举例 W1 = (x - x0); W2 = (x - x0)(x - x1); W3 = (x - x0)(x - x1)(x - x2)
@param:  i  i阶(i次多项式)
@param:  xi  所有插值节点的横坐标集合
@return: 返回Wi(x)函数
"""
def  get_Wi(i  =  0 , xi  =  []):
     def  Wi(x):
         result  =  1.0
         for  each  in  range (i):
             result  * =  (x  -  xi[each])
         return  result
     return  Wi

　　　　

　　　　OK， 牛顿插值法最重要的两部分都有了，下面就是将这两部分组合成牛顿插值函数，如果是c之类的语言就需要保存一些中间数据了，我利用了Python的闭包直接返回一个牛顿插值函数，闭包可以利用到它所处的函数之中的上下文数据。

1
2
3
4
5
6
7
8
9
10
11
"""
@brief: 获得牛顿插值函数
@
"""
def  get_Newton_inter(xi  =  [], fi  =  []):
     def  Newton_inter(x):
         result  =  fi[ 0 ]
         for  i  in  range ( 2 ,  len (xi)):
             result  + =  (get_order_diff_quot(xi[:i], fi[:i])  *  get_Wi(i - 1 , xi)(x))
         return  result
     return  Newton_inter

　　　　上面这段代码就是对牛顿插值函数公式的翻译，注意get_Wi函数的参数是i-1，这个从函数的表达式可以找到原因。

 

　　构造一些插值节点

　

1
2
3
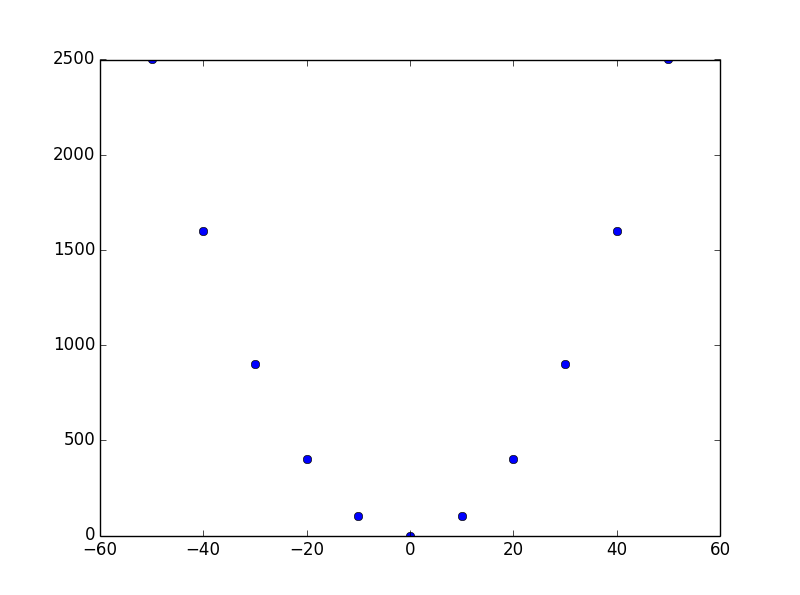
''' 插值节点, 这里用二次函数生成插值节点，每两个节点x轴距离位10 '''
    sr_x  =  [i  for  i  in  range ( - 50 ,  51 ,  10 )]
    sr_fx  =  [i * * 2  for  i  in  sr_x] 

　　　

 

　获得牛顿插值函数

1
2
3
4
Nx  =  get_Newton_inter(sr_x, sr_fx)             # 获得插值函数
 
tmp_x  =  [i  for  i  in  range ( - 50 ,  51 )]           # 测试用例
tmp_y  =  [Nx(i)  for  i  in  tmp_x]                # 根据插值函数获得测试用例的纵坐标

　　

 

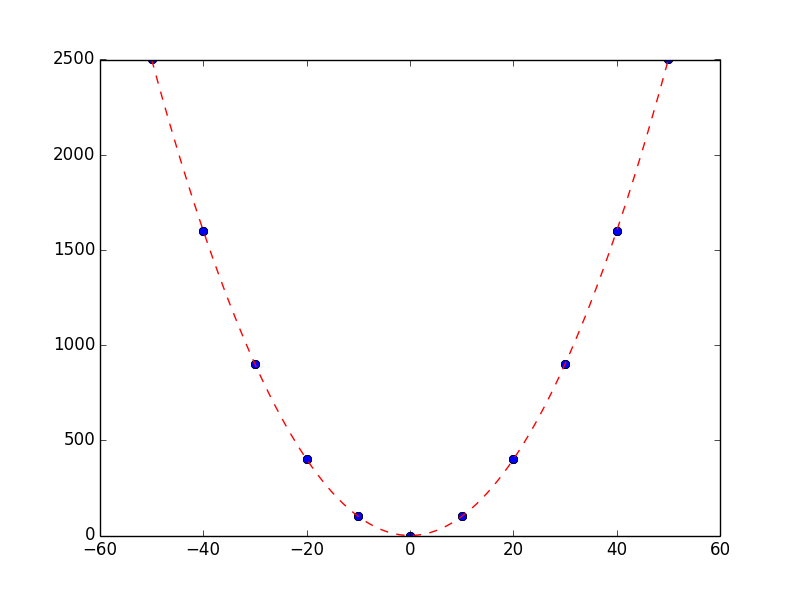
完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
# -*- coding: utf-8 -*-
"""
Created on Thu Nov 17 18:34:21 2016
 
@author: tete
@brief: 牛顿插值法
"""
 
 
import  matplotlib.pyplot as plt
 
"""
@brief:   计算n阶差商 f[x0, x1, x2 ... xn]
@param:   xi   所有插值节点的横坐标集合                                                        o
@param:   fi   所有插值节点的纵坐标集合                                                      /   \
@return:  返回xi的i阶差商(i为xi长度减1)                                                     o     o
@notice:  a. 必须确保xi与fi长度相等                                                        / \   / \
           b. 由于用到了递归，所以留意不要爆栈了.                                           o   o o   o
           c. 递归减递归(每层递归包含两个递归函数), 每层递归次数呈二次幂增长，总次数是一个满二叉树的所有节点数量(所以极易栈溢出)                                                                                    
"""
def  get_order_diff_quot(xi  =  [], fi  =  []):
     if  len (xi) >  2  and  len (fi) >  2 :
         return  (get_order_diff_quot(xi[: len (xi)  -  1 ], fi[: len (fi)  -  1 ])  -  get_order_diff_quot(xi[ 1 : len (xi)], fi[ 1 : len (fi)]))  /  float (xi[ 0 ]  -  xi[ - 1 ])
     return  (fi[ 0 ]  -  fi[ 1 ])  /  float (xi[ 0 ]  -  xi[ 1 ])
     
 
 
 
"""
@brief:  获得Wi(x)函数;
          Wi的含义举例 W1 = (x - x0); W2 = (x - x0)(x - x1); W3 = (x - x0)(x - x1)(x - x2)
@param:  i  i阶(i次多项式)
@param:  xi  所有插值节点的横坐标集合
@return: 返回Wi(x)函数
"""
def  get_Wi(i  =  0 , xi  =  []):
     def  Wi(x):
         result  =  1.0
         for  each  in  range (i):
             result  * =  (x  -  xi[each])
         return  result
     return  Wi
     
     
     
     
"""
@brief: 获得牛顿插值函数
@
"""
def  get_Newton_inter(xi  =  [], fi  =  []):
     def  Newton_inter(x):
         result  =  fi[ 0 ]
         for  i  in  range ( 2 ,  len (xi)):
             result  + =  (get_order_diff_quot(xi[:i], fi[:i])  *  get_Wi(i - 1 , xi)(x))
         return  result
     return  Newton_inter
     
         
 
"""
demo:
"""
if  __name__  = =  '__main__' :  
 
     ''' 插值节点, 这里用二次函数生成插值节点，每两个节点x轴距离位10 '''
     sr_x  =  [i  for  i  in  range ( - 50 ,  51 ,  10 )]
     sr_fx  =  [i * * 2  for  i  in  sr_x] 
     
     Nx  =  get_Newton_inter(sr_x, sr_fx)             # 获得插值函数
     
     tmp_x  =  [i  for  i  in  range ( - 50 ,  51 )]           # 测试用例
     tmp_y  =  [Nx(i)  for  i  in  tmp_x]                # 根据插值函数获得测试用例的纵坐标
        
     ''' 画图 '''
     plt.figure( "I love china" )
     ax1  =  plt.subplot( 111 )
     plt.sca(ax1)
     plt.plot(sr_x, sr_fx, linestyle  =  ' ', marker=' o ', color=' b')
     plt.plot(tmp_x, tmp_y, linestyle  =  '--' , color = 'r' )
     plt.show()
声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/爱喝兽奶帝天荒/article/detail/803881
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号