基于verilog的除法器的实现_verilog除法器

本文应该是目前全网最通俗易懂，而且比较全面的用verilog实现除法器的文章。首先说明一下本文的探讨的重点。我们首先从整数的除法开始讲起，然后慢慢延伸到小数的除法，和负数的除法。

对于一个除法器来说，他的实现框架应该是下面这个图：

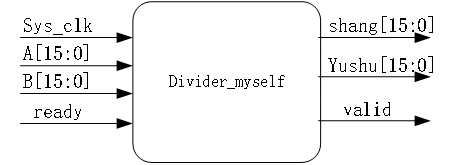
在这个框架图中，A是被除数，B是除数，ready是说明此时的被除数和除数是有效的。而shang和yushu就是字面意思，代表的是除法的结果。而valid指的是此时的除法的结果是有效的。

那么设计完框架图之后 ，现在来设计一下时序图，一个理想的除法器的时序图应该如下所示：

从上图可以看出，在第一个时钟周期的时候输入divisor（除数）和dividend（被除数）之后，此时在下一个时钟周期，intergral（商）和remaider（余数）就会马上出现结果，这当然就是我们想要的时序。那么有没有可能实现这样完美的时序呢？有同学可能会说，这还不简单，直接用“/”运算不就可以了吗？但其实不太行，因为计算机可以很方便的做加减乘，就是不方便做除法，哪怕实现了除法，他的逻辑电路也是很复杂。对于为什么计算机做除法很复杂，可以参考下面这篇文章。

https://www.cnblogs.com/BinB-W/p/5706725.html

那么还是回到刚刚这个问题，如何实现上图中这个完美的除法器时序呢？vivado其实自带了一个divider generator的ip核，他就是能实现这个完美的时序，上图中我就是调用了divider generator，从而实现了这个时序图。在divider generator中，一共有三个模式，分别是Radix2，High Radix，Lutmult。对于这三个模式，在手册中可以查阅到他们的不同点在于延时和所用资源的不同。其中Radix2和Lutmult可以实现一个时钟周期后，结果就马上出现的时序，所以我们重点应该是放在这两个模式怎么用verilog进行实现。

通过查阅手册和查阅源代码，我们发现这两种模式的实现用到了Xilinx的原语，他的实现方式是偏硬件的，而不是通过纯verilog代码实现的。所以我们无法通过复现divider generator这个ip核，来实现完美的时序。

那么现在问题走到这里，接下来该怎么走呢？我们从手册中找到了答案，手册中有这样一句话：

意思是说，在除法器这个ip核中，用到了基2非恢复余数法。那么现在重点应该是放在如何用verilog实现非恢复余数法或者是恢复余数法。

对于恢复余数法，网上有很多文章，实事求是地说，基本上看不明白。我第一次看的时候，也是看的云里雾里的。后来我看了哈工大老师计算机组成原理（B站上有），并且自己手写了一遍除法，才算真的搞懂是什么意思。对于这个方法不理解的同学我建议你先看一下哈工大的这一节课：

我下面直接总结一下恢复余数法。对于恢复余数法，他的本质是描述了手写二进制除法的过程，在进行两个二进制的除法的时候，我们所作的唯一事情就是，给商上0或者上1。那么给商上完1之后，我们需要做什么呢？给商上完0之后，又需要做什么呢？其实只需要做下面两件事情，如下：

从上面的总结可以看出，恢复余数法的本质就是给三个变量赋值，分别是商、余数、除数。其中商的取值取决于余数和除数的大小比较；余数的取值取决于余数和除数的大小比较；除数则是一直右移即可。

有了上面的认识之后，我们可以提取出如下的关键verilog代码：

那么描述完恢复余数法的关键步骤之后，有些同学可能还会疑惑一件事情。在网上的代码中我们常常看到被除数需要左边接上很多0，除数需要右边接上很多0，这是为什么呢？这个问题需要各位同学自己手写一下除法的过程，你才能真正明白。我的建议是你用1100_1100除以11_1001试一下。

那么现在来看看我们的时序图是什么样的：

从图中可以看出我们实现一次除法运算所需要的时钟周期是19个，和完美的时序相差还是比较远，但是没办法，计算机的结构限制了我们只能这样做。如果有同学实在是觉得这样做除法花费的时间太长，我的建议是可以去研究一下SRT算法、牛顿法和 GoldSchmidt 法，这里不再赘述。

讲完整数的除法之后现在来讲讲小数和负数的除法运算。对于小数来说，他其实可以通过乘以一个10，再除以一个10，从而化为了整数的运算。对于负数的除法来说，他需要多考虑一个负数的补码，这里我直接将源代码放在下面，各位同学搞懂了整数的运算，对于小数和负数那不会很难。

最后讲讲恢复余数法和非恢复余数法的区别，这两个的区别我建议是看看哈工大老师的下面这两节课

我总结的这两个方法的区别如下：

最后放上源代码，文章写到后面确实有点赶，因为等下要赶飞机了，有不懂的地方发评论吧。

module division(
    input   wire                 sys_clk,
    input   wire                 rst_n  ,
    input   wire signed  [16:0]              A,
    input   wire signed  [16:0]              B,
    input   wire                   ready,
    
    output  reg  signed  [16:0]          shang,
    output  reg  signed  [16:0]          yushu,
    output  reg                    valid
    
    
    );
 
reg work_flag;
reg [15:0] yushu_qian;
reg [31:0] chushu;
reg [4:0] cnt;
reg [15:0]  shang_qian;
 
always@(posedge sys_clk,negedge rst_n)
    if(!rst_n)
        work_flag <= 1'd0;
    else    if(cnt == 'd16)
        work_flag <= 1'd0;
    else    if(ready == 1'd1)
        work_flag <= 1'd1;
 
always@(posedge sys_clk,negedge rst_n)
    if(!rst_n)
        yushu_qian <= 16'd0;
    else    if(work_flag == 1'd0)
        yushu_qian <= (A[16] == 1'd1)?~A[15:0]+1'd1:A[15:0];
    else    if(work_flag == 1'd1)
        begin
            if(yushu_qian >= chushu)
                yushu_qian <= yushu_qian - chushu;
            else    
                yushu_qian <= yushu_qian;
        end        
        
 
always@(posedge sys_clk,negedge rst_n)
    if(!rst_n)
        chushu <= 32'd0;
    else    if(work_flag == 1'd0)
        chushu <= {(B[16] == 1'd1)?~B[15:0]+1'd1:B[15:0],16'd0};
    else    if(work_flag == 1'd1)
        chushu <= chushu>>1;
 
always@(posedge sys_clk,negedge rst_n)
    if(!rst_n)
        cnt <= 'd0;
    else    if(work_flag == 1'd0)
        cnt <= 'd0;
    else
        cnt <= cnt + 'd1;
 
always@(posedge sys_clk,negedge rst_n)
    if(!rst_n)
        shang_qian <= 16'd0;
    else    if(work_flag == 1'd0)
        shang_qian <= 16'd0;
    else    if(work_flag == 1'd1)
        begin
            if(yushu_qian >= chushu)
                shang_qian[16-cnt] <= 1'd1;
            else    
                shang_qian[16-cnt] <= 1'd0;
        end        
        
always@(posedge sys_clk,negedge rst_n)
    if(!rst_n)
        shang <= 17'd0;
    else    if(cnt == 'd17)
        shang = (A[16]^B[16] == 1'd1)?{1'd1,~shang_qian+1'd1}:shang_qian;     
 
always@(posedge sys_clk,negedge rst_n)
    if(!rst_n)
        yushu <= 17'd0;
    else    if(cnt == 'd17)
        yushu <= {A[16] == 1'd1}? {1'd1,~yushu_qian[15:0]+1'd1} :{1'd0,yushu_qian[15:0]};    
 
always@(posedge sys_clk,negedge rst_n)
    if(!rst_n)
        valid <= 'd0;
    else    if(cnt == 'd17)
        valid <= 'd1;
    else
        valid <= 'd0;
        
endmodule 

`timescale 1ns/1ns
 
module tb_2();
 
reg signed  [16:0]          A;
reg signed  [16:0]           B;
reg sys_clk;
reg rst_n;
reg ready;
 
 
division division_inst(
    .sys_clk            (sys_clk),
    .rst_n              (rst_n),
    .A                  (A     ),
    .B                  (B     ),
    .ready              (ready)
    );
 
always #10 sys_clk = ~sys_clk;
 
 
 
initial begin
    sys_clk = 1'd0;
    rst_n <= 1'd0;
    A <= 16'd0;
    B <= 16'd0;
    ready <= 1'd0;
    #10
    rst_n <= 1'd1;
    #100;
    A <= -17'd27;
    B <= 17'd5;
    ready <= 1'd1;
    #20
    ready <= 1'd0;
    
    #400;
    A <= 17'd33;
    B <= -17'd7;
    ready <= 1'd1;
    #20
    ready <= 1'd0;
    
    #400;
    A <= -17'd39;
    B <= -17'd2;
    ready <= 1'd1;
    #20
    ready <= 1'd0;
    
    #400;
    A <= 17'd17;
    B <= 17'd3;
    ready <= 1'd1;
    #20
    ready <= 1'd0;
    
end   
 
endmodule