Python神经网络识别手写数字-MNIST数据集_基于python语言(numpy科学计算包),实现单个神经元手写数字分类模型。 数据集:mnis

一、手写数字集-MNIST

要让计算机能够识别出来图片的内容是一件十分困难的事情，识别人的手写笔记也不简单，它们不像印刷字符那样清晰明确，因此在识别上带来一定的困难。
要想让神经网络达到预期的效果就需要大量数据进行学习。那数据怎么来，不用自己收集，国外已经有人制作了一个手写数据集MNIST。在下面这个网站就可以下载完整的数据集。
下载链接：MNIST数据集
网站提供了两种CSV文件：训练集、测试集。
下图展示了打开后的CSV部分数据。

数据的第一列是标签，也就是实际上图像代表的数字，如‘2‘。这是我们希望得到的答案。随后的数值，也就是从每一行除了第一个数字以外的数值，代表的每一个像素的灰度值，这个数组的尺寸为28*28。这意味着，标签后面跟随了784个数值。光看数值，我们很难看出这张图片显示的是什么。所以在进行训练之前，我们可以将其转化为图像的形式来确认一下这是手写数字。
利用python打开文件，查看一下数据。

data_file = open("C:/Users/15619/train_file.csv", 'r') # 打开文件
data_list = data_file.readlines()  # 将文件中所有的行读入data_file变量
data_file.close  # 关闭文件
data_list[0] # 查看数据的第一行数
1
2
3
4

最后输出的结果如下：

上图我们可以看到，数据之间用逗号分隔，所有数值大小都处在0-255的范围内。我们接下来会使用下列代码将用逗号分隔的数字转化为数组。

• 用函数按照逗号为分隔标志，将数据拆分成单个数值。
• 利用切片忽略掉第一个数值，剩下的数据就是784个像素值，可以转化为28*28=784的数组。
• imshow绘制数组
  代码如下：

import matplotlib.pyplot 
import numpy
%matplotlib inline
all_values = data_list[0].split(',') 
# 先把数值转化为numpy的类型，然后利用reshape转化为数组
image_array = numpy.asfarray(all_values[1:]).reshape((28,28)) 
matplotlib.pyplot.imshow(image_array, cmap='Greys', interpolation='None')
1
2
3
4
5
6
7

二、数据预处理

输入数据处理

上一节我们知道了如何获取到现成的数据，然后还通过一小段代码输出了一行数据的可视化图像。这节我们来看看如何将数据喂给神经网络。首先要进行下面的处理：

• 将0-255的像素值，缩放到0.01-1之间，选择0.01作为最小值是为了避免先前观察到的0值输入最终会认为地造成权重更新失败。
  首先将像素值/255得到0-1的数值，然后乘以0.99范围变为0-0.99，接着加上0.01，这样可以将整体数值偏移到0.01-1.0。
  实现代码

scaled_input = (numpy.asfarray(all_values[1:])/255.0*0.99)+0.01
print(scaled_input)
1
2

输出数据处理

神经网络的输入数据已经准备就绪了，现在，我们来讨论一下输出的数据以及匹配的正确输出答案。我们采用的是simoid激活函数，该函数无法输出负数或这大于1的数值，且无法达到0或者1，因为它们是两个极限值。因此，我们得对目标值进行一定处理。
我们要实现的目标是能够对图像进行分类，然后系统输出10个数值，分别对应10个结果。这意味这我们需要选择10个节点。数值的标签是0-9之间的一个，当答案是1的时候，我们希望的输出是对应’1‘的一个节点能够输出尽可能接近1的数值，也就是该节点属于激活状态，而其他的节点尽可能处于抑制状态。
下图展示了输出节点的输出示例。

从第一列看，标签是5，输出第六个节点的数值较大，而其他的数值比较小，接近于零。
而最后一列比较有意思，输出的最大数值对应9，而对应4的数值为中等大小。这说明识别对象比较模糊，使得手写字迹难以辨认。通常来说，我们会选择最大的数值作为最后的答案。
现在，我们需要把标签转化为一个目标数组，用于神经网络的训练。比如标签为“5”的节点，其他节点的数值都应该很小，所以我们希望的输出应该是[0,0,0,0,0,1,0,0,0,0]。但是前面我们知道，输出不可能为0或者1，所以我们需要对0和1分别用0.01和0.99来代替。所以最后我们选用的目标输出是[0.01,0.01,0.01,0.01,0.01,0.99,0.01,0.01,0.01,0.01]。
通过下面的代码来实现上述内容：

# 输出节点设定为10
outnodes = 10
# 用zero()函数创建一个用零填充的长度为10的数组。
targets = numpy.zero(outnodes)+ 0.01
# 标签位置的数值用0.99来代替
tartets[int(all_value[0])] = 0.99
1
2
3
4
5
6

三、神经网络的结构选择

输入节点784：图像尺寸是28*28大小，所以选择这个输入节点数。
隐含层节点100：选择100个节点并不是通过什么科学计算的方法得到的。而是，首先我们认为神经网络可以找到输入数据中的特征，而这些特征通常都可以用更为简单的方式来表达，因此隐含层节点选择不会超过输入节点数。而选择数量太少的话，网络能力就会不足。100个节点也不是固定的，选择多少个，最好的办法就是多次实验，然后选择一个合适的数字即可。
输出节点10:由于分类标签有十种结果，所以选择10个节点。

四、训练网络

综合以上描述后的代码如下，我们通过对一个小样本的数据进行训练，打开包含100条数据的csv文件进行网络训练。

import numpy
import scipy.special
import matplotlib.pyplot
%matplotlib inline

class neuralNetwork():
	# 初始化函数
	def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate):
		self.innodes = inputnodes
		self.hinodes = hiddennodes
		self.outnodes = outputnodes
		self.lr = learningrate 
	
		# 链接权重
		# 三个参数：正态分布中心，标准方差，numpy数组大小
		self.winhi = numpy.random.normal(0.0, pow(self.hinodes, -0.5), 		(self.hinodes, self.innodes))
	# 其中0.0是正态分布的中心点，pow(self.hinodes, -0.5)就是对这个隐含层节点数进行开平方。
	# 最后一个参数就是我们希望得到的numpy数组的大小。
		self.whiout = numpy.random.normal(0.0, pow(self.outnodes, -0.5),(self.outnodes, self.hinodes))
	
		# 激活函数
		self.activation_function = lambda x: scipy.special.expit(x)
		pass


	def train(self, inputs_list, targets_list):
		# 把输入列表转化为numpy型的2维
		inputs = numpy.array(inputs_list,ndmin=2).T
		targets = numpy.array(targets_list,ndmin=2).T

		# 计算隐含层输出
		hidden_inputs = numpy.dot(self.winhi, inputs)
		hidden_outputs = self.activation_function(hidden_inputs)
		
		# 计算输出层输出
		final_inputs = numpy.dot(self.whiout, hidden_outputs)
		final_outputs = self.activation_function(final_inputs)

		# 计算输出层的误差
		output_errors = targets - final_outputs
		hidden_errors = numpy.dot(self.whiout.T, output_errors)

		# 更新链接权重
		self.whiout +=self.lr*numpy.dot((output_errors*final_outputs*(1-	final_outputs)), numpy.transpose(hidden_outputs))
# final_outputs已经经过了sigmoid运算，所以可以直接调用。
# 对输入层和隐含层之间的权重进行更新
		self.winhi +=self.lr*numpy.dot((hidden_errors*hidden_outputs*(1.0-hidden_outputs)), numpy.transpose(inputs))


	# 输入的是一个数列例如[1,2,3,4]
	def query(self, inputs_list):
		inputs = numpy.array(inputs_list,ndmin=2).T
		hidden_inputs = numpy.dot(self.winhi, inputs)
	# 经过隐含层的激活函数
		hidden_outputs = self.activation_function(hidden_inputs)
	# 信号从隐含层传递到输出层
		final_outputs = numpy.dot(self.whiout, hidden_outputs)
	# 信号经过输出层的激活函数
		final_outputs = self.activation_function(final_outputs)
		return final_outputs


# 输入节点，隐含层节点，输出节点，学习率
input_nodes = 784
hidden_nodes = 100
output_nodes = 10
learning_rate = 0.3
epochs = 3

# 创建一个神经网络对象
n = neuralNetwork(input_nodes, hidden_nodes, output_nodes,learning_rate)

# 读取训练数据
training_data_file = open("C:/Users/15619/train_file.csv", 'r')
training_data_list = training_data_file.readlines()
training_data_file.close()

# 训练神经网络
for e in range(epochs):
	for record in training_data_list:
		all_values = record.split(',')
		# 输入数据预处理
		inputs = (numpy.asfarray(all_values[1:])/255*0.99)+0.01
		# 目标数据预处理
		targets = numpy.zeros(output_nodes)+0.01
		targets[int(all_values[0])]=0.99
		n.train(inputs, targets)
		pass
	pass
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89

测试网络

上面，我们用了一个100条记录的数据进行网络训练，我们现在可以检测一下网络的效果怎么样。先来使用刚刚训练数据的第一条来进行测验一下。
首先我们要读取数据。

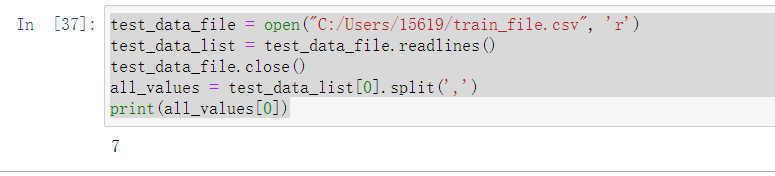
test_data_file = open("C:/Users/15619/train_file.csv", 'r')
test_data_list = test_data_file.readlines()
test_data_file.close()
all_values = test_data_list[0].split(',')
print(all_values[0])
1
2
3
4
5

下面展示了该条数据的正确结果为7.

我们来通过调用网络的query()函数来查询一下神经网络的输出。

test_inputs = (numpy.asfarray(all_values[1:])/255.0*0.99)+0.01
n.query(test_inputs)
1
2

输出的结果如下：

可见，输出的第八个节点，也就是对应’7‘的节点数值比较大，而其他节点输出都比较小。说明网络的识别结果是正确的。
恭喜！我们成功达成了目的。训练神经网络，然后让网络告诉我们图片的内容是什么。这不过是训练数据集的一部分，仅仅使用了100个数据进行训练，这使得识别正确率不会很高。而完整的训练集有60000条记录。所以让我们继续编写代码，来看看神经网络到底有多大的能耐！

测试正确率的函数

下面让我们来写一个可以输出网络测试的正确率的函数

def test_acc(test_data_list):
	rightnum = 0
	allnum = 0
	for record in test_data_list:
		allnum+=1.0
		all_values = record.split(',')
		correct_label = int(all_values[0])
		inputs = (numpy.asfarray(all_values[1:])/255*0.99)+0.01
		outputs = n.query(inputs)
		label = numpy.argmax(outputs)
		if(label == correct_label):
			rightnum+=1.0
		pass
	acc = rightnum/allnum
	print("Accuracy:",acc)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

经过调用函数测试，得到的正确率如下图所示。

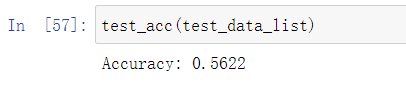
可见正确率不是很高，接下来我们会使用完整的数据进行训练，然后测试一下正确率。看看效果如何吧！

五、完整的训练

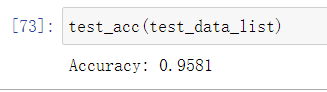
让我们修改一下文件路径，然后就可以对完整的文件进行训练。训练结果如下：

可见，大量的数据对精度提升有着很大的作用，这个表现令人吃惊。几乎是95%的准确率。到这里我们完成了对神经网络的简单尝试，而且取得了非常好的效果。

学习率的调整

后续我们可以继续对网络进行改进，以求得到更高精度的结果。比如我们可以调整隐含层节点，或者学习率。本次训练使用的是0.3的学习率，如果我们尝试了使用0.6的学习率，输出的精度会有所下降，达到0.90。似乎朝着不好的方向发展了。然后尝试调整到0.1，我们发现精度可以高达0.9523,这似乎让网络更好了。
显然学习率的选择对于结果有重要影响，所以选择一个合适的学习率很重要。
下面的图表展示了学习率与正确率的一个曲线关系图。

训练轮数epoch

训练论数是什么意思呢？刚刚开始我也很难明白，觉得数据训练完了就可以了。但是后来才了解到，完整训练完一次成为一个epoch，而多个epoch也会对网络的训练效果有一定影响。
为什么要训练多次呢，其实是为了通过更多调整权值的机会，有利于梯度下降的权值更新。
我们对上面的代码进行改进一下看看。

for e in range(epochs):
	for record in training_data_list:
		all_values = record.split(',')
		# 输入数据预处理
		inputs = (numpy.asfarray(all_values[1:])/255*0.99)+0.01
		# 目标数据预处理
		targets = numpy.zeros(output_nodes)+0.01
		targets[int(all_values[0])]=0.99
		n.train(inputs, targets)
		pass
	pass
1
2
3
4
5
6
7
8
9
10
11

训练结果如下：

由于训练次数提升，电脑运算花费的时间也增加了，我的电脑运行了大概2分钟才得到结果。
上图可见从之前的0.9414提高到了0.951。虽然提升不是很高，但也是巨大进步。从这里我们证实了epoch数量确实会对效果造成一定影响。但是epochs数量是不是越大越好呢。我们来用一个图片展示一下epoch大小对网络精度的影响。

改变网络结构

由于网络结构的输入节点和输出节点已经固定了，因此我们只能通过改变隐含层的节点数来观察结构对网络训练效果的影响。
我们来试图改变一下隐含层节点数，将其从100变道200，然后看看效果怎么样。

效果不是很明显，但是重在有一定提升。下面展示了隐含层节点与网络训练效果之间的关系曲线。

附录代码

import numpy
import scipy.special
import matplotlib.pyplot
%matplotlib inline

class neuralNetwork():
	# 初始化函数
	def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate):
		self.innodes = inputnodes
		self.hinodes = hiddennodes
		self.outnodes = outputnodes
		self.lr = learningrate 
	
		# 链接权重
		# 三个参数：正态分布中心，标准方差，numpy数组大小
		self.winhi = numpy.random.normal(0.0, pow(self.hinodes, -0.5), 		(self.hinodes, self.innodes))
	# 其中0.0是正态分布的中心点，pow(self.hinodes, -0.5)就是对这个隐含层节点数进行开平方。
	# 最后一个参数就是我们希望得到的numpy数组的大小。
		self.whiout = numpy.random.normal(0.0, pow(self.outnodes, -0.5),(self.outnodes, self.hinodes))
	
		# 激活函数
		self.activation_function = lambda x: scipy.special.expit(x)
		pass


	def train(self, inputs_list, targets_list):
		# 把输入列表转化为numpy型的2维
		inputs = numpy.array(inputs_list,ndmin=2).T
		targets = numpy.array(targets_list,ndmin=2).T

		# 计算隐含层输出
		hidden_inputs = numpy.dot(self.winhi, inputs)
		hidden_outputs = self.activation_function(hidden_inputs)
		
		# 计算输出层输出
		final_inputs = numpy.dot(self.whiout, hidden_outputs)
		final_outputs = self.activation_function(final_inputs)

		# 计算输出层的误差
		output_errors = targets - final_outputs
		hidden_errors = numpy.dot(self.whiout.T, output_errors)

		# 更新链接权重
		self.whiout +=self.lr*numpy.dot((output_errors*final_outputs*(1-	final_outputs)), numpy.transpose(hidden_outputs))
# final_outputs已经经过了sigmoid运算，所以可以直接调用。
# 对输入层和隐含层之间的权重进行更新
		self.winhi +=self.lr*numpy.dot((hidden_errors*hidden_outputs*(1.0-hidden_outputs)), numpy.transpose(inputs))


	# 输入的是一个数列例如[1,2,3,4]
	def query(self, inputs_list):
		inputs = numpy.array(inputs_list,ndmin=2).T
		hidden_inputs = numpy.dot(self.winhi, inputs)
	# 经过隐含层的激活函数
		hidden_outputs = self.activation_function(hidden_inputs)
	# 信号从隐含层传递到输出层
		final_outputs = numpy.dot(self.whiout, hidden_outputs)
	# 信号经过输出层的激活函数
		final_outputs = self.activation_function(final_outputs)
		return final_outputs

# 测试网络效果的函数
def test_acc(test_data_list):
	rightnum = 0
	allnum = 0
	for record in test_data_list:
		allnum+=1.0
		all_values = record.split(',')
		correct_label = int(all_values[0])
		inputs = (numpy.asfarray(all_values[1:])/255*0.99)+0.01
		outputs = n.query(inputs)
		label = numpy.argmax(outputs)
		if(label == correct_label):
			rightnum+=1.0
		pass
	acc = rightnum/allnum
	print("Accuracy:",acc)


# 输入节点，隐含层节点，输出节点，学习率，训练轮数
input_nodes = 784
hidden_nodes = 200
output_nodes = 10
learning_rate = 0.3
epochs = 3

# 创建一个神经网络对象
n = neuralNetwork(input_nodes, hidden_nodes, output_nodes,learning_rate)

# 读取训练数据
training_data_file = open("C:/Users/15619/Downloads/mnist_train.csv", 'r')
training_data_list = training_data_file.readlines()
training_data_file.close()

# 训练神经网络
for e in range(epochs):
	for record in training_data_list:
		all_values = record.split(',')
		# 输入数据预处理
		inputs = (numpy.asfarray(all_values[1:])/255*0.99)+0.01
		# 目标数据预处理
		targets = numpy.zeros(output_nodes)+0.01
		targets[int(all_values[0])]=0.99
		n.train(inputs, targets)
		pass
	pass

# 读取测试数据
test_data_file = open("C:/Users/15619/Downloads/mnist_test.csv", 'r')
test_data_list = test_data_file.readlines()
test_data_file.close()

# 调用函数
test_acc(test_data_list)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114