信息与内容安全实验一 对抗样本攻击实验_信息对抗算法实验报告

对抗样本攻击实验

实验摘要

题目1:

根据 PyTorch 官网教程中 Adversarial Example Generation 章节内容，完整实现 Fast
Gradient Sign Attack (FGSM)算法。 网址：
https://pytorch.org/tutorials/beginner/fgsm_tutorial.html

题目描述

题目 1：
根据在 PyTorch 官网教程的“Adversarial Example Generation” 章节中学习和理解快速梯度符号攻击算法，并将其实现为完整的 PyTorch 代码。
FGSM（fast gradient sign method）是一种基于梯度生成对抗样本的算法，属于对抗攻击中的无目标攻击（即不要求对抗样本经过model预测指定的类别，只要与原样本预测的不一样即可），该算法通过在原始数据上添加一定的扰动，使得神经网络在对抗样本上的分类结果与原始样本不同。具体实现过程可以参考官网教程中的代码，其中需要计算梯度并对输入数据进行扰动，最终得到对抗样本。

实验内容

1.实验原理

fast gradient sign method是一种基于梯度生成对抗样本的算法, 属于对抗攻击中的无目标攻击, 即不要求对抗样本经过model预测指定的类别, 只要与原样本预测的不一样即可. 它旨在通过利用模型学习的方式和渐变来攻击神经网络, 攻击调整输入数据以基于相同的反向传播梯度来最大化损失, 而不是通过基于反向传播的梯度调整权重来最小化损失. 简而言之, 攻击是利用损失函数的梯度, 然后调整输入数据以最大化损失.

FGSM公式:
$$\eta =ϵsign\left({\nabla }_{x}J(\theta ,x,y)\right)$$
在公式中,x是原始样本;θ是模型的权重参数, 即w;y是x的真实类别. 输入原始样本, 权重参数以及真实类别, 通过J损失函数求得神经网络的损失值, ∇x表示对x求偏导, 即损失函数J对x样本求偏导。sign是符号函数, 即sign(-1), sign(-99.9)等都等于-1; sign(1), sign(99.9)等都等于1。epsilon的值通常是人为设定, 可以视作学习率, 一旦扰动值超出阈值, 该对抗样本会被人眼识别。

2.实验步骤

2.1实验环境

Windows11 Python=3.7 pytorch=1.12.1 torchvision=0.13.1 torchaudio=0.12.1 cudatoolkit=11.6

2.2 引入相关包和预训练模型

from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
import numpy as np
import matplotlib.pyplot as plt
epsilons = [0, .05, .1, .15, .2, .25, .3]#epsilon值
pretrained_model = "./data/lenet_mnist_model.pth"#预训练模型
use_cuda=True#是否使用cuda
1
2
3
4
5
6
7
8
9
10
11

2.3搭建被攻击的模型

# 定义LeNet网络
class Net(nn.Module):#继承nn.Module类
    def __init__(self):
        super(Net, self).__init__()#调用父类的构造函数
        self.conv1 = nn.Conv2d(1, 10, kernel_size=5)#定义卷积层
        self.conv2 = nn.Conv2d(10, 20, kernel_size=5)#定义卷积层
        self.conv2_drop = nn.Dropout2d()#定义dropout层
        self.fc1 = nn.Linear(320, 50)#定义全连接层
        self.fc2 = nn.Linear(50, 10)#定义全连接层
        
    #定义前向传播函数    
    def forward(self,x):
        x=F.relu(F.max_pool2d(self.conv1(x),2))#第一层卷积，池化，激活
        x=F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)),2))#第二层卷积，池化，激活
        x=x.view(-1,320)#展平
        x=F.relu(self.fc1(x))#第一层全连接，激活
        x=F.dropout(x,training=self.training)#dropout
        x=self.fc2(x)#第二层全连接
        return F.log_softmax(x,dim=1)#log_softmax
        
#MINIST数据集测试和加载
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=False, download=True, transform=transforms.Compose([
            transforms.ToTensor(),
            ])),
        batch_size=1, shuffle=True)
#查看是否配置GPU，没有就调用CPU
print("CUDA Available:",torch.cuda.is_available())
device = torch.device("cuda" if (use_cuda and torch.cuda.is_available()) else "cpu")

#初始化网络
model=Net().to(device)

#加载预训练模型
model.load_state_dict(torch.load(pretrained_model, map_location='cpu'))

#设置模型为测试模式
model.eval()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

输出当前网络结构

2.4 FGSM模块

# FGSM攻击代码
def fgsm_attack(image, epsilon, data_grad):
    # 收集数据梯度的元素符号
    sign_data_grad = data_grad.sign()
    # 通过调整输入图像的每个像素来创建扰动图像
    perturbed_image = image + epsilon*sign_data_grad
    # 添加剪切以维持[0,1]范围
    perturbed_image = torch.clamp(perturbed_image, 0, 1)
    # 返回被扰动的图像
    return perturbed_image
1
2
3
4
5
6
7
8
9
10

2.5 测试函数

用于测试模型在给定epsilon值下的对抗样本的准确，其中将数据的requires_grad属性设置为True，这是为了攻击很关键，因为需要计算损失函数对输入数据的梯度。并调用FGSM攻击，生成受扰乱的图像，然后重新分类受扰乱的图像，获取最终预测结果，如果最终预测结果与标签一致，则认为攻击成功，计数器加1，最终返回返回正确率和对抗样本。

def test(model,device,test_loader,epsilon):
    # 精度计数器
    corrent=0#正确的数量
    adv_examples=[]#存储攻击成功的样本
    # 循环遍历测试集中的所有示例
    for data,target in test_loader:
        # 将数据和标签发送到设备
        data,target=data.to(device),target.to(device)
        # 设置张量的requires_grad属性，这对于攻击很关键
        data.requires_grad=True
        # 通过模型前向传递数据
        output=model(data)
        init_pred=output.max(1,keepdim=True)[1]#获取初始预测结果
        # 如果初始预测是错误的，不打断攻击，继续
        if init_pred.item()!=target.item():
            continue
        
        # 计算损失
        loss=F.nll_loss(output,target)
        
        # 将所有现有的渐变归零，作用是清除上一次的梯度
        model.zero_grad()
        # 计算后向传递模型的梯度,计算出各个参数的梯度
        loss.backward()
        # 收集datagrad 为了攻击
        data_grad=data.grad.data
        
        # 调用FGSM攻击
        perturbed_data=fgsm_attack(data,epsilon,data_grad)
        
        # 重新分类受扰乱的图像
        output=model(perturbed_data)
        
        # 检查是否成功
        final_pred=output.max(1,keepdim=True)[1]#获取最终预测结果
        if final_pred.item()==target.item():
            corrent+=1
            # 保存0 epsilon示例的特例
            if (epsilon==0) and (len(adv_examples)<5):
                adv_ex=perturbed_data.squeeze().detach().cpu().numpy()
                adv_examples.append((init_pred.item(),final_pred.item(),adv_ex))
        else:#保存epsilon>0的样本
            if len(adv_examples)<5:
                adv_ex=perturbed_data.squeeze().detach().cpu().numpy()
                adv_examples.append((init_pred.item(),final_pred.item(),adv_ex))
        
    #计算最终的正确率
    final_acc=corrent/float(len(test_loader))
    print("Epsilon:{}\tTest Accuracy={}/{}={}".format(epsilon,corrent,len(test_loader),final_acc))
    
    #返回正确率和对抗样本
    return final_acc,adv_examples 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

2.6可视化对比
在这里，我们对 ϵ 输入中的每个 ϵ 值运行完整的测试步骤。对于每个 ϵ，我们还保存了最终的准确性和一些成功的对抗性示例，这些示例将在接下来的部分中绘制。

accuracies=[]
examples=[]

# 对于每个epsilon，运行测试
for eps in epsilons:
    acc,ex=test(model,device,test_loader,eps)
    accuracies.append(acc)
    examples.append(ex)

plt.figure(figsize=(5,5))
plt.plot(epsilons, accuracies, "*-")
plt.yticks(np.arange(0, 1.1, step=0.1))
plt.xticks(np.arange(0, .35, step=0.05))
plt.title("Accuracy vs Epsilon")#准确率与epsilon的关系
plt.xlabel("Epsilon")
plt.ylabel("Accuracy")
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

2.7 实验样本可视化

# 画出几个epsilon的示例
cnt=0#计数器
plt.figure(figsize=(8,10))#画布大小
for  i in range(len(epsilons)):#遍历epsilon
    for j in range(len(examples[i])):
        cnt+=1
        plt.subplot(len(epsilons),len(examples[0]),cnt)
        plt.xticks([],[])
        plt.yticks([],[])
        if j==0: #第一行的标题
            plt.ylabel("Eps:{}".format(epsilons[i]),fontsize=14)
        orig,adv,ex=examples[i][j]#获取原始，对抗，样本
        plt.title("{} -> {}".format(orig,adv),color=("green" if orig==adv else "red"),fontsize=14)
        plt.imshow(ex,cmap="gray")
plt.tight_layout()#自动调整子图参数，使之填充整个图像区域
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

3.实验结果与分析

3.1 准确性与扰动Epsilon对比

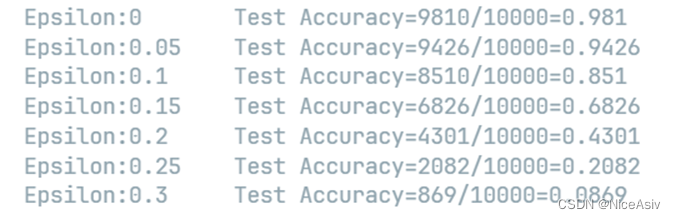
可以看到随着 Epsilon 的增加，我们预计测试精度会降低。但是我们还是需予以权衡，因为这会导致扰动变得更易被识别，因为看着图片更怪异了。

3.2 扰动前后的数据集识别

在上面我们对部分识别结果进行可视化，我们在每个$ϵ$ 上展示一些成功的对抗示例价值。图的每一行都显示不同的 $ϵ$ 值。第一个行是 $ϵ=0$ 示例，表示原始“干净”的图像，无扰动。每个图像的标题显示原始分类 ->对抗性分类。请注意，扰动在 $ϵ=0.15$ 时开始变得明显，并且在 $ϵ=0.3$ 变得相当明显。