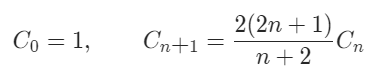【LeetCode】96. 不同的二叉搜索树【卡特兰数】_卡特兰数 leetcode

题目链接：https://leetcode-cn.com/problems/unique-binary-search-trees/

题目描述

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

测试用例

示例 1：

输入：n = 3
输出：5

示例 2：

输入：n = 1
输出：1

提示：

1 <= n <= 19

题解

方法一：动态规划

定一个有序序列 1 ⋯ n，为了构建出一棵二叉搜索树，我们可以遍历每个数字 i，将该数字作为树根，将 1 ⋯ (i−1) 序列作为左子树，将 (i+1) ⋯ n 序列作为右子树。接着我们可以按照同样的方式递归构建左子树和右子树。

在上述构建的过程中，由于根的值不同，因此我们能保证每棵二叉搜索树是唯一的。

由此可见，原问题可以分解成规模较小的两个子问题，且子问题的解可以复用。因此，我们可以想到使用动态规划来求解本题。

DP方法原文链接：https://leetcode-cn.com/problems/unique-binary-search-trees/solution/bu-tong-de-er-cha-sou-suo-shu-by-leetcode-solution/

 方法二：卡特兰数

代码

// 卡特兰数
class Solution {
    public int numTrees(int n) {
        long res = 1;
        for (int i = 0; i < n; i++){
            res = 2 * res * (2 * i + 1) / (i + 2);
        }
        return (int)res;
    }
}

拓展

 其他卡特兰数的应用，大致分为几类：

• 括号化问题（或者01个数问题）

矩阵链乘： P=a1×a2×a3×……×an，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？(h(n)种)

• 出栈次序问题

一个栈(无穷大)的进栈序列为1,2,3,…n,有多少个不同的出栈序列?
　　(1)有2n个人排成一行进入剧场（或者商店买东西）。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？(将持5元者到达视作将5元入栈，持10元者到达视作使栈中某5元出栈)
　　(2)在圆上选择2n个点,将这些点成对连接起来，使得所得到的n条线段不相交的方法数。

• 凸多边形问题

（1）一个凸的n边形，用直线连接他的两个顶点使之分成多个三角形，每条直线不能相交，问一共有多少种划分方案。
(2)类似：一位大城市的律师在她住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果她从不穿越（但可以碰到）从家到办公室的对角线，那　　 么有多少条可能的道路？
　 (3)类似：在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?
例如n+2个点的凸多边形，这里n=4，通过卡特兰数的推导可以得出h(4)=14。 

• 给定节点组成二叉树的问题

给定N个节点，能构成多少种形状不同的二叉树？
先去一个点作为顶点,然后左边依次可以取0至N-1个相对应的,右边是N-1到0个,两两配对相乘,就是h(0)*h(n-1) + h(2)*h(n-2) +…+ h(n-1)h(0)=h(n)（能构成h(N)个）

• nn棋盘从左下角走到右上角而不穿过主对角线的走法

a.在 nn的格子中，只在下三角行走，每次横或竖走一格，有多少中走法？其实向右走相当于进栈， 向左走相当于出栈，本质就是n个数出栈次序的问题，所以答案就是卡特兰数。（利用这个模型，我们解决这个卡特兰问题的变形问题，并顺便给进出栈问题的解法一个几何解释）

b.有n+1个叶子的满二叉树的个数？事实上，向左记为+1，向右记为−1，按照向左优先的原则，从根节点开始遍历．例如第一个图记为+1,+1,+1,−1,−1,−1,于是由卡特兰数的含义可得满二叉树的个数为Cn。
感觉a，b差不多属于同一种类型。。。

拓展内容的原文链接：https://blog.csdn.net/weixin_44565518/article/details/99731190