李宏毅机器学习第二十二周周报GAN理论2

week22 Theory behind GAN 2

摘要

本文主要讨论了GAN的理论知识。本文介绍了在GAN模型的训练过程。本文分别阐述了生成器与分辨器的训练细节，并详细描述了整体算法进行。其次本文展示了题为DeGAN : Data-Enriching GAN for Retrieving Representative Samples from a Trained Classifier的论文主要内容。这篇论文提出了DeGAN，该模型可以使用相关领域的数据或者相关性不高的数据生成数据并能利用数据进行较为准确的预测。该文使用CIFAR和MNIST验证了其优越性。最后，本文基于python实现了ARIMA并用于预测时序数据。

Abstract

This article mainly discusses the theoretical knowledge of GAN. This article describes the training process of GAN. This article describes the training details of the generator and the discriminator, and the overall algorithm. Secondly, this article presents the main content of the paper entitled DeGAN: Data-Enriching GAN for Retrieving Representative Samples from a Trained Classifier. The paper proposes DeGAN, a model that can generate data from relevant fields or data that is not highly correlated, and can use the data to make more accurate predictions. This paper uses CIFAR and MNIST to verify its superiority. Finally, this article implements ARIMA based on python and uses to predict time series data.

一、李宏毅机器学习

0.上周内容概述

在开始本周的学习之前，先简要回顾一下上周的内容。

在GAN模型之前主要使用最大似然估计来处理生成式问题，即对于一个可从中采样的数据分布$P_{data}(x)$，使用由参数$\theta$控制的分布$P_G(x;\theta )$进行拟合。由其公式推导得，似然估计最大化即KL散度最小化。

GAN模型主要包含两个部分：生成器、分辨器。前者通过学习使得生成分布与真实分布的散度最小化。后者的学习目标与JS散度有一定相似性。

1.GAN的训练过程

本周从GAN模型的训练过程开始

生成器与分辨器的目标如下
$$\begin{gathered} G^{\ast }=arg\underset{G}{\min }\underset{D}{\max }V(G,D) \\ {D}^{\ast }=arg\underset{D}{\max }V(D,G) \end{gathered}$$
训练过程

• 初始化生成器与分辨器
• 在每个循环内
  1. 固定G，更新D
  2. 固定D，更新G

若使用上周推导的形式，则该训练过程是以JS散度为衡量标准的优化过程

2.生成器与分辨器的算法细节

令$L(G)={\max }_{D}V(G,D)$，则目标是确定一个G使得损失函数L(G)的值最小化，从而有梯度下降算法如下
$${\theta }_G\leftarrow {\theta }_G-\eta \partial L(G)/\partial {\theta }_G{\theta }_G\text{defines}G$$

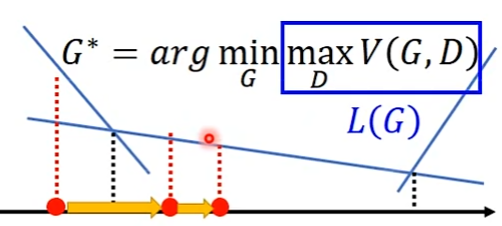
对于如何最小化一最大值函数，假设有最大化目标函数如上图，则其是分段函数，在一个区间上只需对该区间对应的函数求导作梯度下降即可

其梯度上升算法如下

• 给定$G_0$
• 确定$D_0^{\ast }$使得$V(G_0,D)$最大化
  • $V(G_0,D_0^{\ast })$是$P_{data}(x)$与$P_{G_0}(x)$的JS散度
• 使用上述算法获得$G_1$
• 确定$D_1^{\ast }$使得$V(G_1,D)$最大化
  • $V(G_1,D_1^{\ast })$是$P_{data}(x)$与$P_{G_0}(x)$的JS散度

一般认为上述过程会使得JS散度下降。虽然确定了生成器函数使得JS散度取到最值，但是由于分辨器函数改变，其并不一定是下降的。因此通常假设分辨器函数的迭代并不会使得其函数发生较大的变化，从而可以认为该过程使得JS散度下降。

在实际过程中

• 给定G，计算${\max }_{D}V(G,D)$

  • 从真实数据中采样 { x 1 , x 2 , … , x m } \{x^1,x^2,\dots,x^m\} {x1,x2,…,xm}，使用生成器生成 { x ~ 1 , x ~ 2 , … , x ~ m } \{\tilde x^1,\tilde x^2,\dots,\tilde x^m\} {x~1,x~2,…,x~m}。则有

  • $$\text{Maximize}\tilde{V}=\frac{1}{m}\sum _{i=1}^{m}logD(x^i)+\frac{1}{m}\sum _{i=1}^{m}log(1-D({\tilde{x}}^i))$$

可以将D看作一个二分类器，真实数据为其正例、生成数据为其负例，D的目标是使得其交叉熵最小化（即将上述公式最大化）。

3.整体算法描述

基于上述描述，对训练过程做一个较为完备的描述

• 在每个循环内

  • 首先更新D，重复k次，k为超参

  • 从真实数据中采样 { x 1 , x 2 , … , x m } \{x^1,x^2,\dots,x^m\} {x1,x2,…,xm}

  • 从前置的噪声分布中采样 { z 1 , z 2 , … , z m } \{z^1,z^2,\dots,z^m\} {z1,z2,…,zm}

  • 获取生成数据 { x ~ 1 , x ~ 2 , … , x ~ m } \{\tilde x^1,\tilde x^2,\dots,\tilde x^m\} {x~1,x~2,…,x~m}，${\tilde{x}}^i=G(z^i)$

  • 更新分辨器参数${\theta }_D$使得$\tilde{V}$最大化，$\tilde{V}$公式以及${\theta }_d$更新方式如下

    • $\tilde{V}=\frac{1}{m}{\sum }_{i=1}^{m}logD(x^i)+\frac{1}{m}{\sum }_{i=1}^{m}log(1-D({\tilde{x}}^i))$
    • ${\theta }_d\leftarrow {\theta }_d=\eta \nabla \tilde{V}({\theta }_d)$

  • 其次更新G，仅一次，因为更新次数过多会使得函数变化太大，而使得分辨器无法最小化JS散度

  • 从前置的噪声分布中另外采样m个数据 { z 1 , z 2 , … , z m } \{z^1,z^2,\dots,z^m\} {z1,z2,…,zm}

  • 更新生成器参数${\theta }_g$以最小化$\tilde{V}$，其公式以及${\theta }_g$更新方式如下

  • $$\tilde{V}=\frac{1}{m}\sum _{i=1}^{m}logD(x^i)+\frac{1}{m}\sum _{i=1}^{m}log(1-D(G(z^i)))$$

    由于上述公式仅第二项与${\theta }_g$相关，故在更新时，可以仅计算第二项

  • ${\theta }_g\leftarrow {\theta }_g-\eta \nabla \tilde{V}({\theta }_g)$

4.原文中生成器目标函数的实现方式

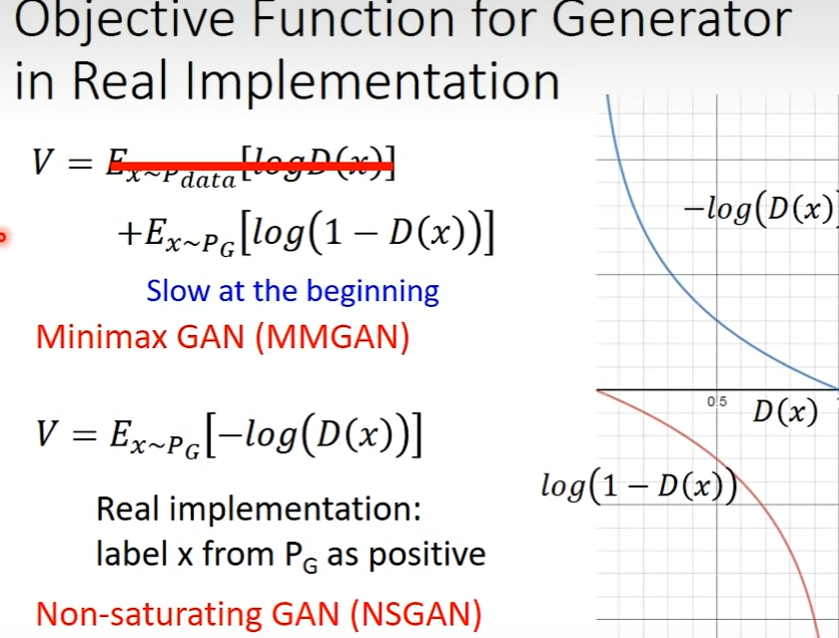
若使用上述的方式进行优化会得到$V=E_{x\sim P_G}[log(1-D(x))]$，即MMGAN

论文作者认为，采用该方式会使得在初始阶段的梯度较小，图像如下图红线，因此采用了蓝线的实现方式，即$V=E_{x\sim P_G}[-log(D(x))]$，该网络是NSGAN。（但在实际操作中二者效果相近）

tips:在实际过程中，除了使用本次生成器结果之外，还可以使用以往的生成器结果。

二、文献阅读

1. 题目

题目：DeGAN : Data-Enriching GAN for Retrieving Representative Samples from a Trained Classifier

作者：Lantao Yu, Weinan Zhang, Jun Wang, Yong Yu

链接：https://arxiv.org/abs/1912.11960

期刊：AAAI2020

2. abstract

多样化的数据集可用于训练初始模型，但由于数据隐私问题或内存限制，在整个产品生命周期中存储它可能不可行。作者建议为给定训练网络的未来学习任务弥合丰富的可用数据和缺乏相关数据之间的差距。作者证明，可以利用来自相关领域的数据来实现基准数据集上的无数据知识蒸馏和增量学习任务的最先进性能。作者进一步证明，作者提出的框架可以丰富任何数据，甚至来自不相关领域的数据，使其对给定网络的未来学习任务更有用。

A diverse dataset may be used for training an initial model, but it may not be feasible to store it throughout the product life cycle due to data privacy issues or memory constraints. Authors propose to bridge the gap between the abundance of available data and lack of relevant data, for the future learning tasks of a given trained network. Authors demonstrate that data from a related domain can be leveraged to achieve state-of-the-art performance for the tasks of Data-free Knowledge Distillation and Incremental Learning on benchmark datasets. Authors further demonstrate that our proposed framework can enrich any data, even from unrelated domains, to make it more useful for the future learning tasks of a given network.

3. 网络架构

3.1无数据生成方法

下图左侧说明了具有所需附加约束的经典无数据生成方法。为了提高多样性，该架构可以包括一个多样性执行网络，其作用是构建从生成器的输出空间到输入空间的一对一映射。其中间路径显示了使用生成器和预训练分类器生成样本的经典无数据方法。

由于分类器是多对一映射函数，因此基于输出激活最大化来检索输入的经典方法可能会导致生成分布远离真实数据分布的图像。对生成的图像施加额外的统计特征可以使图像的分布更接近真实数据的分布。然而，要施加的约束对于所考虑的数据集来说是非常特定的。手工制定这些约束的过程可能很乏味，并且需要了解大量有关原始训练数据集的先验知识。

虽然可以使用独立网络或损失函数来施加上述约束，但这会导致复杂性增加。本文通过智能地利用框架中的单个网络（鉴别器）来强制执行相同的约束，这即是本文所提出的 DeGAN。

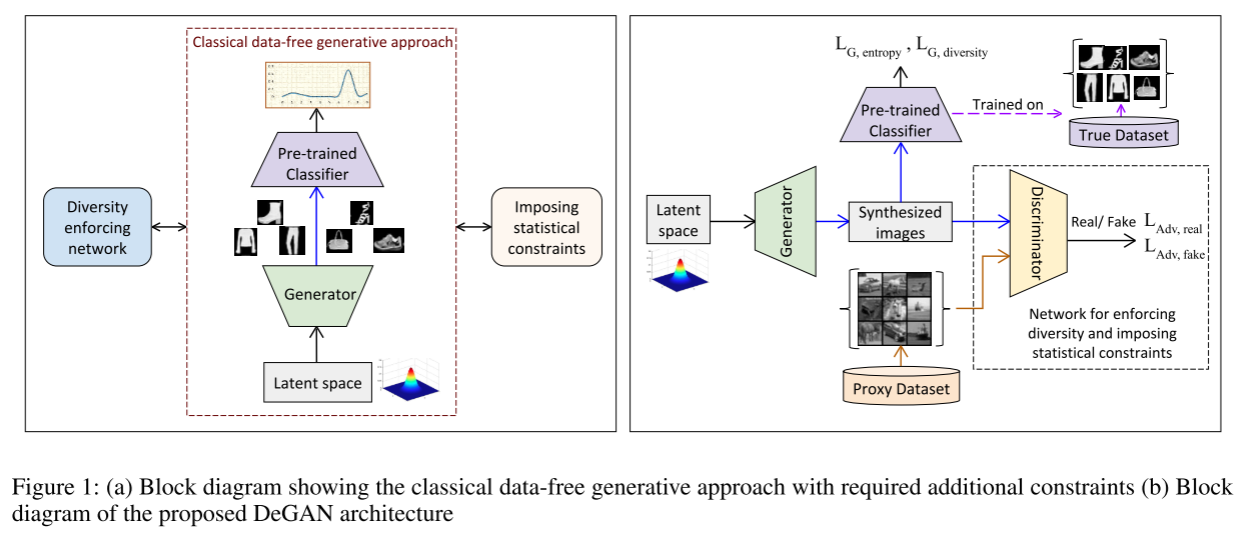
3.2 Data-Enriching GAN(DeGAN)

生成式对抗网络能够有效的施加约束，因此，引入了一个鉴别器，作为上图左侧的施加统计约束块。由于假设原始训练数据不可用，因此使用来自相关领域的数据（代理数据）以对抗性方式训练。其背后的基本原理是，对于来自相同或相关领域的数据，图像的低级统计数据保持相同或相似。因此，GAN 训练确保生成的图像位于代理数据的分布上，这与真实数据的分布类似。 GAN 的训练方法和架构取得了重大进展，以确保生成图像的多样性。本文中使用深度卷积 GAN (DCGAN)（Radford、Metz 和 Chintala 2015）进行实验^[2]

为了确保学习到的分布接近真实数据分布，使用耦合在一起的生成器、分辨器和分类器组成的三方数据丰富化GAN。生成器和鉴别器的权重是可训练的，而分类器的权重是冻结的。

鉴别器确保生成的数据的分布接近代理数据集的分布。分类器的作用是确保生成的数据包含分类器期望在输入图像中出现的特征。分类器还确保生成的图像的分布在所有类别中是平衡的。

损失函数如下

若代理数据集接近真实数据集，则${\lambda }_e$可设置为零。相应的，两者差别较大时，设置为较大值。生成图像的类分布和置信度为调整这些超参数提供了线索。

4. 文献解读

4.1 Introduction

数据的不可用性限制了未来对训练模型的增强。这个问题推动了针对特定任务的有限数据和无数据学习方法的研究。无数据方法的主要问题是它们在严格受限的环境中运行，假设任何附加数据都不可用。这通常会导致使用激活最大化的变体重建样本的过程，这会导致计算成本的上升。本文提出了一种数据丰富 GAN (DeGAN) 框架来丰富任何可用数据，使其对预训练分类器的未来学习任务更加有用。DeGAN 不仅能够生成一组不同的样本，而且还可以通过仅使用一个类数据生成所有类的代表性样本来处理类不平衡问题。

4.2 创新点

1. 提出了用于丰富数据的DeGAN
2. 使用该网络在CIFAR10和Fashion MNIST上展示无数据知识蒸馏结果，证明了数据生成方法的可扩展性
3. 作者表明了其网络结构可以通过不相关领域的数据来进行数据丰富
4. 演示了无数据单步增量学习任务的最先进性能

4.3 实验过程

4.3.1 知识蒸馏实验

训练集-验证集比例为80-20。收敛标准为基于验证准确性的提前停止条件。使用 Singh (2019)^[3] 的 DCGAN 实现作为参考来实现 DeGAN。训练 GAN 的学习率设置为 0.0002，并训练固定数量的 epoch（所有情况下为 200）以确保一致性。经过训练的生成器用于执行知识蒸馏的任务，知识蒸馏损失权重为1。学习率和训练批次在 DCGAN 和 DeGAN 的训练中保持相同。

下图为基于CIFAR的实验结果，使用DeGAN能够有效提升DCGAN的效果。

为了了解方法的真正潜力，考虑相关数据集不可用的情况。使用SVHN颜色数据集

该实验证明了对生成的图像实施良好先验的重要性。这也表明 DeGAN 框架可以丰富任何可用的代理数据，使其对给定任务更有用。

4.3.2 类别增量学习

CIFAR-100 数据集上的单步类增量学习。使用 DeGAN 生成的数据可用于替换各种任务的真实数据集。初始模型首先在 20 个类的随机集合上进行训练，这些类被称为旧类。目标是在无数据的环境中逐步学习下一组 20 个类，其中假设旧类数据不可用。使用 ResNet-32（He et al. 2016）架构作为初始和最终模型。使用的标准损失（Li and Hoiem 2017）：用于学习新类的交叉熵损失和用于避免旧类发生灾难性遗忘的蒸馏损失。添加了一个正则化项来解释新旧类之间 logitstic 的相对缩放。使用提出的 DeGAN 来提取旧类的代表性样本，并使用新类数据作为代理数据。生成的数据用于蒸馏损失部分，以避免旧类出现特别严重的遗忘。

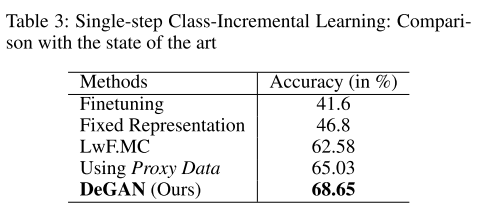
上表中的结果表明，相对于其他无数据基线，准确性显着提高。

4.4 结论

该文提出了一种新颖的数据丰富 GAN (DeGAN) 框架来丰富来自任何领域的数据，使其更适合给定训练分类器的未来任务。从经过训练的分类器中检索代表性样本的问题在知识蒸馏、增量学习、可视化和对抗性扰动的制作等多种应用中非常重要。在几个基准数据集上对框架进行了实证评估，以证明可以使用来自相关领域的数据来实现无数据知识蒸馏任务的最先进结果。观察到，使用相关领域数据生成的样本也可以作为真实数据集的有用可视化。

三、实验内容

使用ARIMA模型预测中国银行股票数据走势

1.数据展示

pandas version 1.5.3，使用loc函数处理，若是较早版本，则使用ix函数

import pandas as pd
import matplotlib.pyplot as plt
ChinaBank = pd.read_csv('ChinaBank.csv',index_col = 'Date',parse_dates=['Date'])
 
#ChinaBank.index = pd.to_datetime(ChinaBank.index)
sub = ChinaBank['2014-01':'2014-06']['Close']
train = sub.loc['2014-01':'2014-03']
test = sub.loc['2014-04':'2014-06']
plt.figure(figsize=(10,10))
print(train)
plt.plot(train)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12

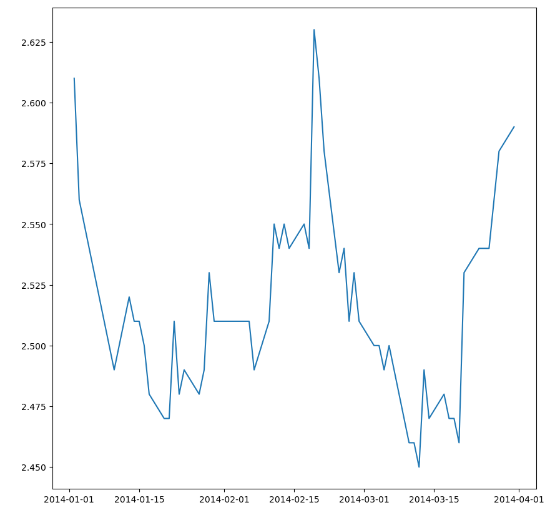
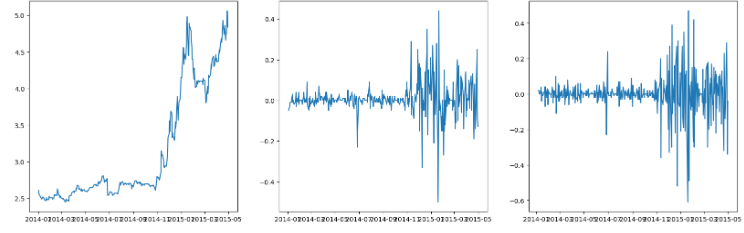
2.使用差分法预测

该方法使得数据更加平稳

ChinaBank['Close_diff_1'] = ChinaBank['Close'].diff(1)
ChinaBank['Close_diff_2'] = ChinaBank['Close_diff_1'].diff(1)
fig = plt.figure(figsize=(20,6))
ax1 = fig.add_subplot(131)
ax1.plot(ChinaBank['Close'])
ax2 = fig.add_subplot(132)
ax2.plot(ChinaBank['Close_diff_1'])
ax3 = fig.add_subplot(133)
ax3.plot(ChinaBank['Close_diff_2'])
plt.show()
1
2
3
4
5
6
7
8
9
10

3.ARIMA模型建立过程

首先介绍AR以及MA模型，然后描述ARMA模型，最后解释ARIMA模型

自回归模型AR：自回归模型描述当前值与历史值之间的关系，用变量自身的历史时间数据对自身进行预测。自回归模型必须满足平稳性的要求。
$$y_t=\mu +\sum _{i=1}^p{\gamma }_i{y}_{t-i}+{ϵ}_t$$
上式为p阶自回归模型的公式定义，$y_t$是当前值,$\mu$是常数项,p是阶数 ${\gamma }_i$是自相关系数,${ϵ}_t$是误差。

移动平均模型MA：移动平均模型关注的是自回归模型中的误差项的累加 ，q阶自回归过程的公式定义如下
$$y_t=\mu +{ϵ}_t+\sum _{i=1}^q{\theta }_i{ϵ}_{t-i}$$
自回归移动平均模型ARMA：自回归模型AR和移动平均模型MA模型相结合，自回归移动平均模型ARMA(p,q)，计算公式如下
$$y_t=\mu +\sum _{i=1}^p\gamma )i{y}_{t-i}+{ϵ}_t+\sum _{i=1}^q{\theta }_i{ϵ}_{t-1}$$
差分自回归移动平均模型ARIMA：将自回归模型、移动平均模型和差分法结合。

该模型通过三个参数、两个函数来控制

自相关函数ACF：描述时间序列观测值与其过去的观测值之间的线性相关性。计算公式如下
$$ACF(k)={\rho }_k=\frac{\text{Cov}(y_t,y_{t-k})}{\text{Var}(y_t)}$$
k为滞后期数

偏自相关函数PACF：描述在给定中间观测值的条件下，时间序列观测值预期过去的观测值之间的线性相关性。假设k=3，那么我们描述的是yt和yt-3之间的相关性，但是这个相关性还受到yt-1和yt-2的影响。PACF剔除了这个影响，而ACF包含这个影响。

数据的拖尾和截尾情况:

import statsmodels.api as sm
fig = plt.figure(figsize=(12,8))
 
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(train, lags=20,ax=ax1)
ax1.xaxis.set_ticks_position('bottom')
fig.tight_layout()
 
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(train, lags=20, ax=ax2)
ax2.xaxis.set_ticks_position('bottom')
fig.tight_layout()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13

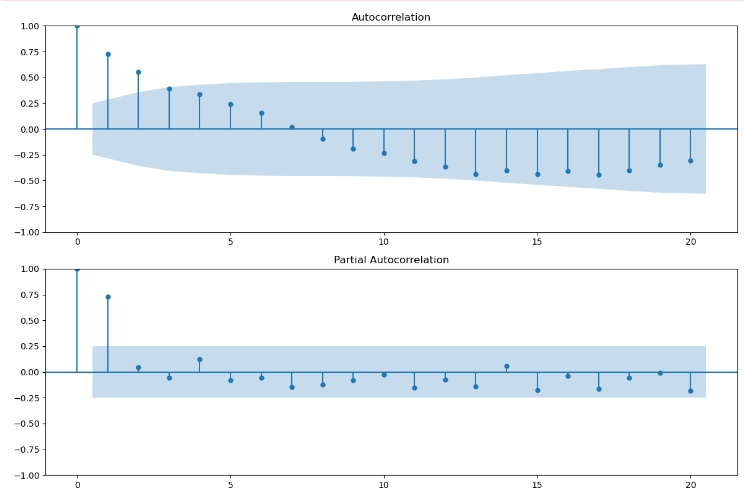
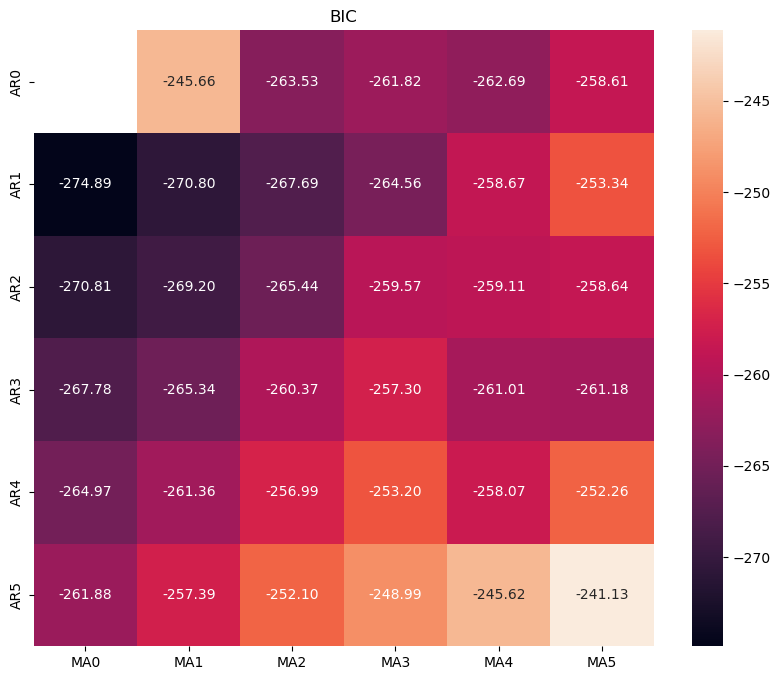
根据信息准则函数法，来确定模型的阶数。预测误差通常用平方误差即残差平方和来表示。
常用的信息准则函数法：

• AIC准则：由模型参数的个数以及模型的极大似然函数确定
• BIC准则：额外考虑了样本容量

使用BIC进行测试

#遍历，寻找适宜的参数
import itertools
import numpy as np
import seaborn as sns
 
p_min = 0
d_min = 0
q_min = 0
p_max = 5
d_max = 0
q_max = 5
 
# Initialize a DataFrame to store the results,，以BIC准则
results_bic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                           columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
 
for p,d,q in itertools.product(range(p_min,p_max+1),
                               range(d_min,d_max+1),
                               range(q_min,q_max+1)):
    if p==0 and d==0 and q==0:
        results_bic.loc['AR{}'.format(p), 'MA{}'.format(q)] = np.nan
        continue
 
    try:
        model = sm.tsa.ARIMA(train, order=(p, d, q),
                               #enforce_stationarity=False,
                               #enforce_invertibility=False,
                              )
        results = model.fit()
        results_bic.loc['AR{}'.format(p), 'MA{}'.format(q)] = results.bic
    except:
        continue
results_bic = results_bic[results_bic.columns].astype(float)
 
fig, ax = plt.subplots(figsize=(10, 8))
ax = sns.heatmap(results_bic,
                 mask=results_bic.isnull(),
                 ax=ax,
                 annot=True,
                 fmt='.2f',
                 )
ax.set_title('BIC')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

4.模型预测

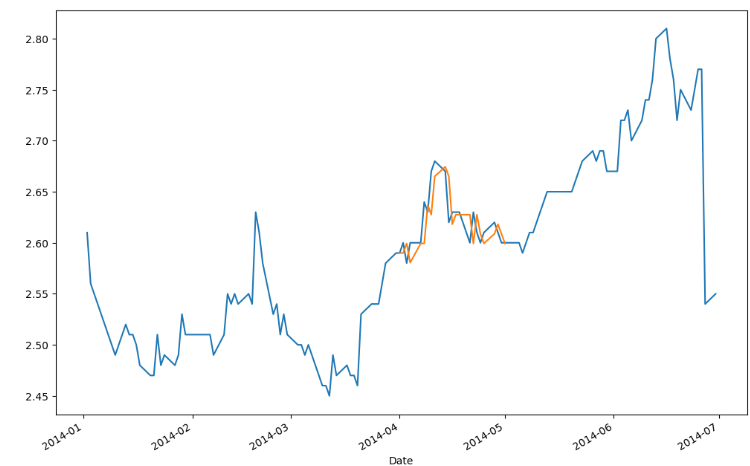
model = sm.tsa.ARIMA(sub, order=(1, 0, 0))
results = model.fit()
predict_sunspots = results.predict(start=str('2014-04'),end=str('2014-05'),dynamic=False)
print(predict_sunspots)
fig, ax = plt.subplots(figsize=(12, 8))
ax = sub.plot(ax=ax)
predict_sunspots.plot(ax=ax)
plt.show()
1
2
3
4
5
6
7
8

小结

本周主要学习了GAN模型训练过程，并阅读了DeGAN论文，最后使用ARIMA模型预测时序数据。下周预计继续学习GAN模型或者BERT

参考文献

[1]Addepalli, Sravanti, et al. “Degan : Data-Enriching Gan for Retrieving Representative Samples from a Trained Classifier.” arXiv.Org, 27 Dec. 2019, arxiv.org/abs/1912.11960.

[2]Radford, A.; Metz, L.; and Chintala, S. 2015. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv preprint arXiv:1511.06434.

[3]Singh, C. 2019. Pretrained gans in pytorch for mnist/cifar. Srinivas, S., and Babu, R. V. 2015. Data-free parameter pruning for deep neural networks. arXiv preprint arXiv:1507.06149.
v preprint arXiv:1511.06434.

[3]Singh, C. 2019. Pretrained gans in pytorch for mnist/cifar. Srinivas, S., and Babu, R. V. 2015. Data-free parameter pruning for deep neural networks. arXiv preprint arXiv:1507.06149.