LeetCode -- 动态规划_leetcode 由来

题目来源：
来源：力扣（LeetCode）
链接：https

动态规划纲要

主要思想：将问题拆分成多个子问题，然后找到最优的子结构；
自顶向下：递归解题思路，可以优化为记忆化搜索；
自底向上：动态规划思路；

一、斐波拉切数列

1.爬楼梯（Easy）

第2次
题目链接：爬楼梯
题目描述：
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
注意：给定 n 是一个正整数。

解题思路：
满足f(n) = f(n-1)+f(n-2)，举例来说明，比如要爬8阶楼梯，可以先爬上7阶楼梯，然后再爬一阶楼梯，这种方式实现的数目与爬7阶楼梯一致；也可以先爬上6阶楼梯，然后再一次性爬2阶楼梯，这种方式实现的数目与爬6阶楼梯一致；所以，f(8) = f(7)+f(6)；
解法一：建立长度为n的动态数组，将得到的方法数量填到对应的数组中，最后返回nums[n-1];
解法二：不用建立数组，创建两个变量pre1和pre2，在for循环里创建一个变量cur = pre1 + pre2，然后让pre1 =cur，pre2 = pre1，巧妙地实现；
解法三：递归；
代码：
解法一：

    public int climbStairs(int n) {
   
        int[] nums = new int [n];
        if(n < 2){
   
            return n;
        }
        nums[0] = 1;
        nums[1] = 2;
        for(int i=2; i < n; i++){
   
            nums[i] = nums[i-1] + nums[i-2];
        }
        return nums[n-1];
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

解法二：

public int climbStairs(int n) {
   
    if (n <= 2) {
   
        return n;
    }
    int pre2 = 1, pre1 = 2;
    for (int i = 2; i < n; i++) {
   
        int cur = pre1 + pre2;
        pre2 = pre1;
        pre1 = cur;
    }
    return pre1;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

2. 打家劫舍（Easy）

第4次
题目链接：打家劫舍
题目描述：
你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

解题思路：
定义 dp 数组用来存储最大的抢劫量，其中 dp[i] 表示抢到第 i 个住户时的最大抢劫量。由于不能抢劫邻近住户，如果抢劫了第 i -1 个住户，那么就不能再抢劫第 i 个住户，所以得到如下公式：

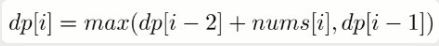
代码：
递归解法：

    public int rob(int[] nums) {
   
        return fun(nums,0);
    }
    
    public int fun(int[] nums,int x){
   
        
        if(x >= nums.length)
            return 0;
        
        int temp = 0;
        for(int i = x; i < nums.length; i++){
   
            temp = Math.max(temp,nums[i] + fun(nums,i+2));
        }
        return temp;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

记忆化搜索：

    public int rob(int[] nums) {
   
        int[] dp = new int[nums.length+1];
        Arrays.fill(dp,-1);
        return fun(nums,0,dp);
    }
    
    public int fun(int[] nums,int x,int[] dp){
   
        
        if(x >= nums.length)
            return 0;
        
        int temp = 0;
        if(dp[x] != -1)
            return dp[x];
        for(int i = x; i < nums.length; i++){
   
            temp = Math.max(temp,nums[i] + fun(nums,i+2,dp));
        }
        dp[x] = temp;
        return temp;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

动态规划：
这里定义的pre2（也即dp[i-2]）为截止到上上一个住户盗窃的最大值，pre1（也即dp[i-1]）为截止到上一个用户盗窃的最大值；
参考代码：

public int rob(int[] nums) {
   
    int pre2 = 0, pre1 = 0;
    for (int i = 0; i < nums.length; i++) {
   
        int cur = Math.max(pre2 + nums[i], pre1);
        pre2 = pre1;
        pre1 = cur;
    }
    return pre1;
}
1
2
3
4
5
6
7
8
9
10
11

我的代码1：从后向前考虑

    public int rob(int[] nums) {
     //从后向前考虑
        int n = nums.length;
        if(n == 0)
            return 0;
        else if(n == 1)
            return nums[0];
        else if(n == 2){
   
            return Math.max(nums[0],nums[1]);
        }
        int[] dp = new int[n+1];
        dp[n-1] = nums[n-1];
        dp[n-2] = Math.max(nums[n-1],nums[n-2]);
        
        for(int i = n-3; i >= 0; i--){
   
            dp[i] = Math.max(nums[i] + dp[i+2],nums[i+1] + dp[i+3]);
        }
        return dp[0];
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

我的代码2：从前向后考虑（稍微改进一下，将dp[i-1]和dp[i-2]分别用pre1和pre2表示，则变成参考代码）

    public int rob(int[] nums) {
      //从前向后考虑
        int n = nums.length;
       if(n == 0)
            return 0;
        else if(n == 1)
            return nums[0];
        
        int[] dp = new int[n];
        dp[0] = nums[0];
        dp[1] = Math.max(nums[0],nums[1]);
        for(int i = 2; i < nums.length; i++){
   
            dp[i] = Math.max(nums[i] + dp[i-2],dp[i-1]);
        }
        return dp[n-1];
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

3. 打家劫舍 II（Medium）

第2次
题目链接：打家劫舍 II
题目描述：
你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

解题思路：由于数组的第一个数和最后一个相邻，所以只能取其中一个，因此考虑数组拆分成两种情况，即从0 ~ nums.length - 2 与从1 ~ nums.length - 1，然后这两部分可以看成是两条直的街道盗窃，可以采用（2. 打家劫舍）中的方法进行求解；
代码：

class Solution {
   
    public int rob(int[] nums) {
   
        if(nums.length == 1){
   
            return nums[0];
        }
        return Math.max(robfind(nums,1,nums.length),robfind(nums,0,nums.length-1));
    }
    
    public int robfind(int[] nums, int a, int b){
   
        int pre2 = 0;
        int pre1 = 0;
        for(int i = a; i < b; i++){
   
            int cur = Math.max(pre2 + nums[i],pre1);
            pre2 = pre1;
            pre1 = cur;
        }
        return pre1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

4. 信件错排（待补充）

第0次
题目链接：来源未知

5. 母牛生产

第0次
题目链接：来源未知
题目描述：假设农场中成熟的母牛每年都会生 1 头小母牛，并且永远不会死。第一年有 1 只小母牛，从第二年开始，母牛开始生小母牛。每只小母牛 3 年之后（即达到3岁）成熟又可以生小母牛。给定整数 N，求 N 年后牛的数量。（假设：第2年小母牛可以生小母牛，每年的年初开始生小母牛，到该年结束，小母牛1岁）；
解题思路：
dp[i] 表示第i年时的牛数量，dp[i-3]表示在第i年能生育的小母牛，dp[i-1]表示上一年的小母牛数量；

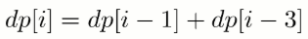
代码：暂无

二、矩阵路径

1.最小路径和（Medium，题号：64）

注意：千万不要陷入思维旋涡！！！
第1次
题目链接：最小路径和
题目描述：
给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

解题思路：
解法一：使用动态规划的解法，定义一个动态数组dp[]长度大小为n，dp[i]表示走到最后一行的第i列所走的最短路径和，使用双重for循环，第一层循环指的是走第i行，先走第一行（即i=0），得到一组dp[]，然后再走第二行，更新dp[]，在走第二行第一列的时候，dp[0]不需要跟别的数比较，直接拿自己加上grid[i][j]就完事，之后dp[j]需要跟dp[j-1]比较（如下图所示），来决定用哪个去加上grid[i][j]，最后返回dp数组的最后一个元素dp[n-1]。

解法二：递归，时间超限制
代码：
解法一：

    public int minPathSum(int[][] grid) {
   
        if(grid == null || grid[0] == null){
   
            return 0;
        }
        int m = grid.length;
        int n = grid[0].length;
        int[] dp = new int[n];
        
        for(int i= 0; i < m; i++
1
2
3
4
5
6
7
8
9
10