devbox
2023面试高手
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

【动态规划】—— 背包模型_完全背包求方案数模板

作者：2023面试高手 | 2024-06-08 13:33:30

赞

踩

完全背包求方案数模板

回顾一下 01 背包问题 （每个物品只能选一次）

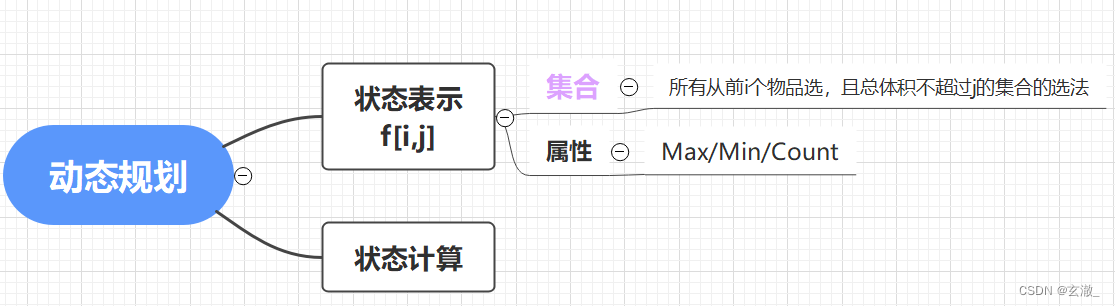
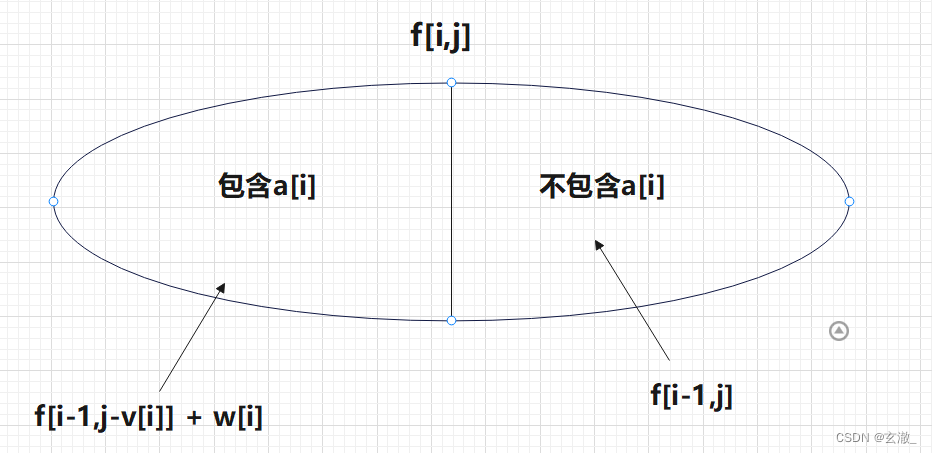
集合划分的依据：用“最后一步”来划分 

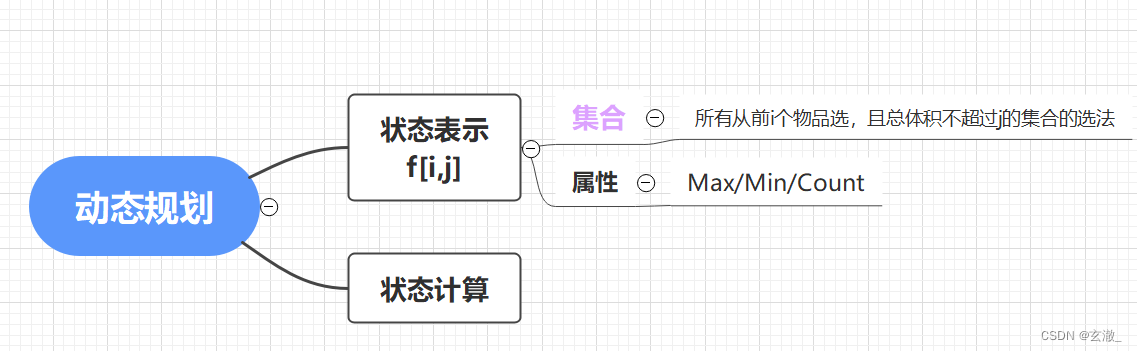
 完全背包问题：每个物品可以选 0,1,2,3... 个

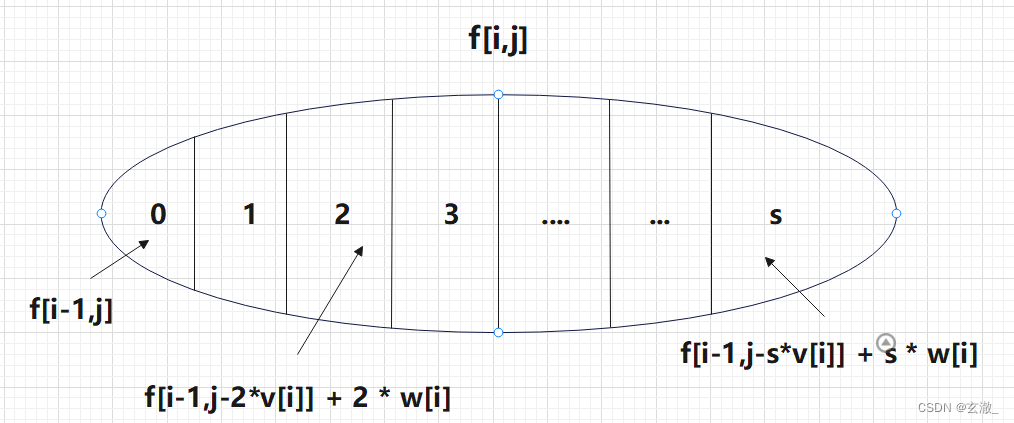
 通过比较可以得到：

f[i,j]=max(f[i-1,j],f[i,j-v]+w)

背包问题的注意事项 

  1. 当空间优化到1维之后，只有完全背包问题的体积是从小到大循环的       
  2. for 物品
        for 体积
            for 决策

AcWing 6. 多重背包问题 III 

 

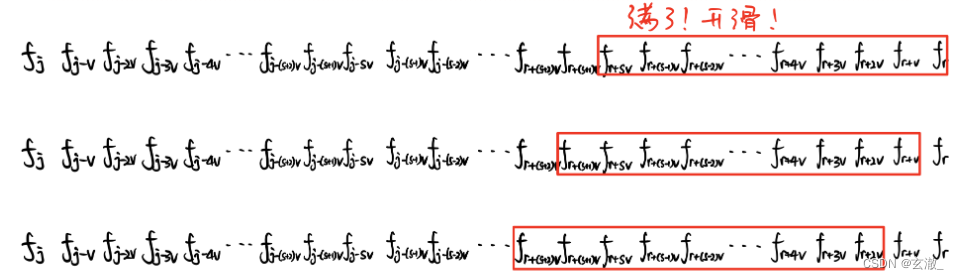
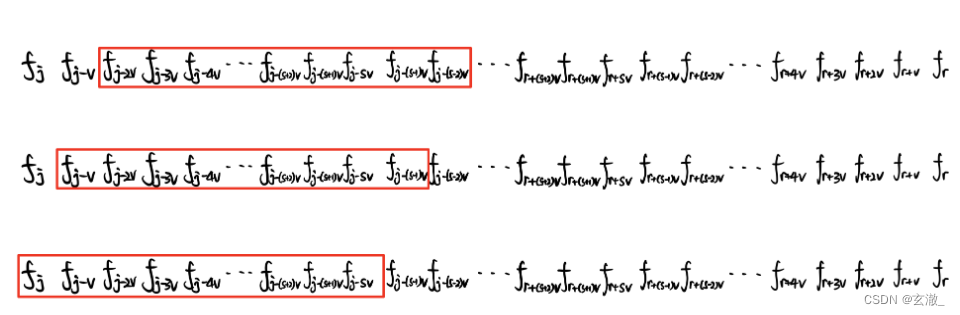
  1. #include <cstring>
  2. #include <iostream>
  3. #include <algorithm>
  4.  
  5. using namespace std;
  6.  
  7. const int N = 20010;
  8.  
  9. int n, m;
  10. int f[N], g[N], q[N];
  11.  
  12. int main()
  13. {
  14.     cin >> n >> m;
  15.     for (int i = 0; i < n; i ++ )
  16.     {
  17.         int v, w, s;
  18.         cin >> v >> w >> s;
  19.         memcpy(g, f, sizeof f);
  20.         for (int j = 0; j < v; j ++ )
  21.         {
  22.             int hh = 0, tt = -1;
  23.             for (int k = j; k <= m; k += v)
  24.             {
  25.                 if (hh <= tt && q[hh] < k - s * v) hh ++ ;
  26.                 while (hh <= tt && g[q[tt]] - (q[tt] - j) / v * w <= g[k] - (k - j) / v * w) tt -- ;
  27.                 q[ ++ tt] = k;
  28.                 f[k] = g[q[hh]] + (k - q[hh]) / v * w;
  29.             }
  30.         }
  31.     }
  32.  
  33.     cout << f[m] << endl;
  34.  
  35.     return 0;
  36. }

AcWing 423. 采药 

  1. 70 3
  2. 71 100
  3. 69 1
  4. 1 2

输出样例：

3

这是01背包问题的简单应用 

  1. #include <iostream>
  2.  
  3. using namespace std;
  4.  
  5.  
  6. const int N = 1010;
  7.  
  8. int n, m;
  9. int f[N];
  10.  
  11. int main()
  12. {
  13.     cin >> m >> n;
  14.     for(int i = 0; i < n; i ++ )
  15.     {
  16.         int v, w;
  17.         cin >> v >> w;
  18.         for(int j = m; j >= v; j -- ) f[j] = max(f[j], f[j - v] + w);
  19.     }
  20.     
  21.     cout << f[m] << endl;
  22.     
  23.     return 0;
  24. }

AcWing 1024. 装箱问题 

输入样例：

  1. 24
  2. 6
  3. 8
  4. 3
  5. 12
  6. 7
  7. 9
  8. 7

输出样例:

0

  1. #include <iostream>
  2. #include <algorithm>
  3.  
  4. using namespace std;
  5.  
  6. const int N = 200010;
  7.  
  8. int m, n;
  9. int f[N];
  10.  
  11. int main()
  12. {
  13.     cin >> m >> n;
  14.     for(int i = 0; i < n; i ++ )
  15.     {
  16.         int v;
  17.         cin >> v;
  18.         for(int j = m; j >= v; j --) f[j] = max(f[j], f[j - v] + v);
  19.     }
  20.     
  21.     cout << m - f[m] << endl;
  22.     return 0;
  23. }

AcWing 1022. 宠物小精灵之收服 

 

输入样例1：

  1. 10 100 5
  2. 7 10
  3. 2 40
  4. 2 50
  5. 1 20
  6. 4 20

输出样例1：

3 30

输入样例2：

  1. 10 100 5
  2. 8 110
  3. 12 10
  4. 20 10
  5. 5 200
  6. 1 110

输出样例2：

0 100
  1. 花费1：精灵球的数量
  2. 花费2：皮卡丘的体力值
  3. 价值：小精灵的数量

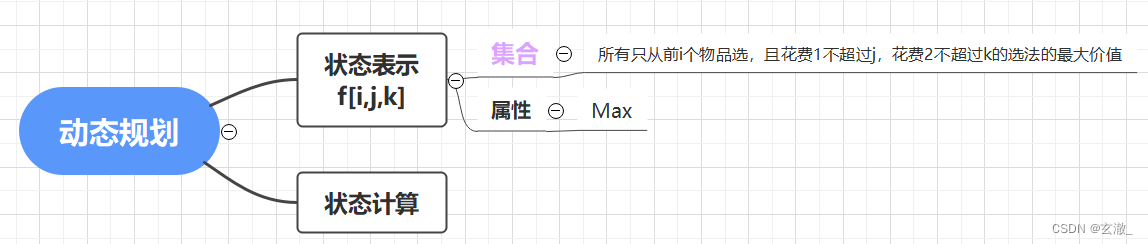
状态计算：

f[i,j,k]=max(f[i-1,j,k],f[i-1,j-v1[i],k-v2[i]]+1)

最多收服的小精灵数量：f[K,N,K]

最小消耗的体力：f[K,N,m]==f[K,N,M]

  1. #include <iostream>
  2. #include <algorithm>
  3.  
  4. using namespace std;
  5.  
  6. const int N = 1010, M = 510;
  7.  
  8. int n, V1, V2;
  9. int f[N][M];
  10.  
  11. int main()
  12. {
  13.     cin >> V1 >> V2 >> n;
  14.     for(int i = 0; i < n; i ++ )
  15.     {
  16.         int v1, v2;
  17.         cin >> v1 >> v2;
  18.         for(int j = V1; j >= v1; j -- )
  19.             for(int k = V2; k >= v2; k --)
  20.                 f[j][k] = max(f[j][k], f[j - v1][k - v2] + 1);
  21.     }
  22.  
  23.     cout << f[V1][V2 - 1] << ' ';
  24.     int k = V2 - 1;
  25.     while(k > 0 && f[V1][k - 1] == f[V1][V2 - 1]) k --;
  26.     cout << V2 - k << endl;
  27.  
  28.     return 0;
  29. }

AcWing 8. 二维费用的背包问题 

输入样例

  1. 4 5 6
  2. 1 2 3
  3. 2 4 4
  4. 3 4 5
  5. 4 5 6

输出样例：

8

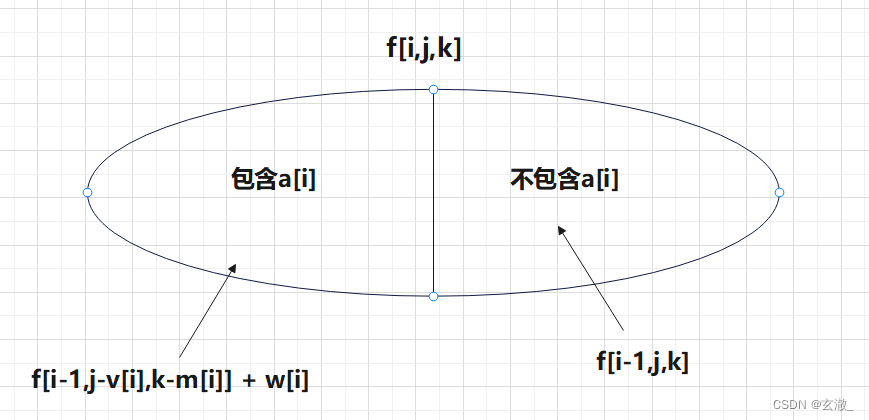
  1. #include <iostream>
  2. #include <algorithm>
  3.  
  4. using namespace std;
  5.  
  6. const int N = 110;
  7.  
  8. int n, V, M;
  9. int f[N][N];
  10.  
  11. int main()
  12. {
  13.     cin >> n >> V >> M;
  14.     for(int i = 0; i < n; i ++ )
  15.     {
  16.         int v, m, w;
  17.         cin >> v >> m >> w;
  18.         for(int j = V; j >= v; j -- )
  19.             for(int k = M; k >= m; k -- )
  20.                 f[j][k] = max(f[j][k], f[j - v][k - m] + w);
  21.     }
  22.     
  23.     cout << f[V][M] << endl;
  24.     
  25.     return 0;
  26. }

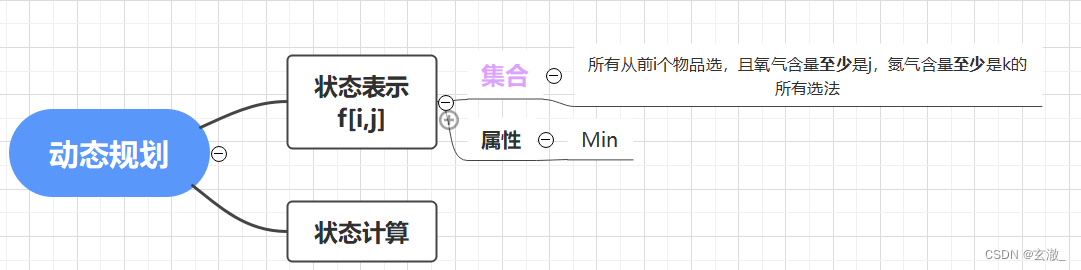
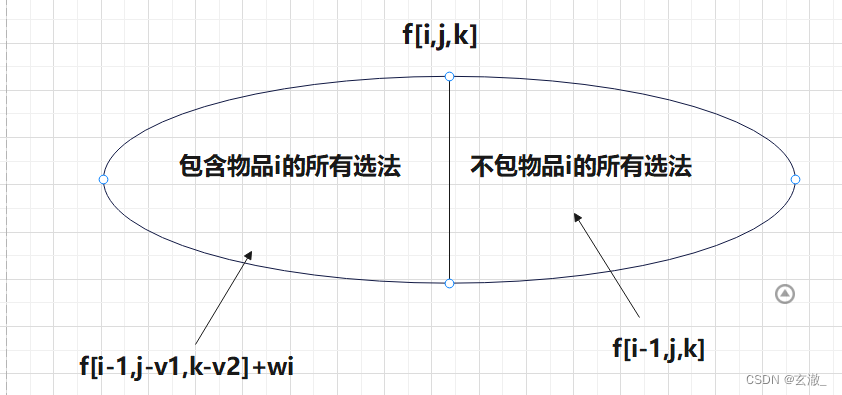
AcWing 1020. 潜水员 

输入样例：

  1. 5 60
  2. 5
  3. 3 36 120
  4. 10 25 129
  5. 5 50 250
  6. 1 45 130
  7. 4 20 119

输出样例：

249

  1. #include <cstring>
  2. #include <iostream>
  3.  
  4. using namespace std;
  5.  
  6. const int N = 22, M = 80;
  7.  
  8. int n, m, K;
  9. int f[N][M];
  10.  
  11. int main()
  12. {
  13.     cin >> n >> m >> K;
  15.     memset(f, 0x3f, sizeof f);
  16.     f[0][0] = 0;
  17.  
  18.     while (K -- )
  19.     {
  20.         int v1, v2, w;
  21.         cin >> v1 >> v2 >> w;
  22.         for (int i = n; i >= 0; i -- )
  23.             for (int j = m; j >= 0; j -- )
  24.                 f[i][j] = min(f[i][j], f[max(0, i - v1)][max(0, j - v2)] + w);
  25.     }
  26.  
  27.  
  28.     cout << f[n][m] << endl;
  29.  
  30.     return 0;
  31. }

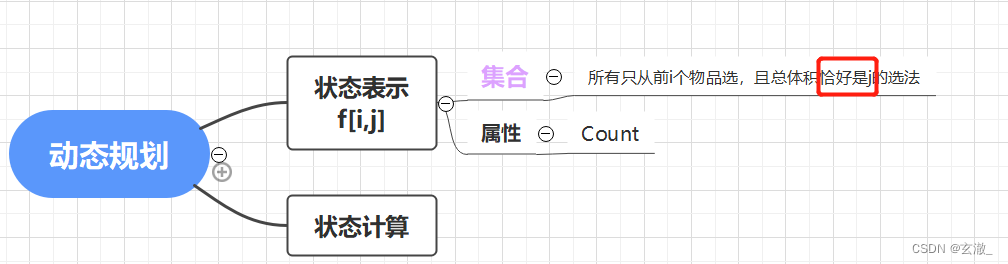
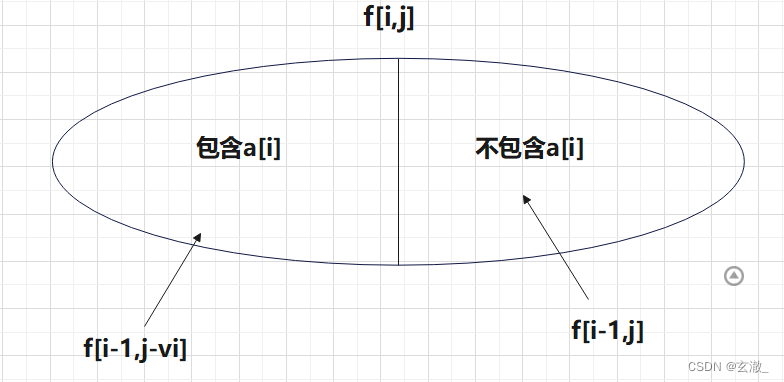
 AcWing 278. 数字组合

输入样例：

  1. 4 4
  2. 1 1 2 2

输出样例：

3

将 M 看成是背包容量

每个数看成是一个物品，Ai 看成是体积

目标：求出总体积恰好是 M 的方案数 

  1. #include <iostream>
  2.  
  3. using namespace std;
  4.  
  5. const int N = 100010;
  6.  
  7. int n, m;
  8. int f[N];
  9.  
  10. int main()
  11. {
  12.     cin >> n >> m;
  13.     f[0] = 1;
  14.     
  15.     for(int i = 0; i < n; i ++ )
  16.     {
  17.         int v;
  18.         cin >> v;
  19.         for(int j = m; j >= v; j -- )
  20.             f[j] += f[j - v];
  21.     }
  22.     
  23.     cout << f[m] << endl;
  24.     
  25.     return 0;
  26. }

AcWing 1019. 庆功会 

输入样例：

  1. 5 1000
  2. 80 20 4
  3. 40 50 9
  4. 30 50 7
  5. 40 30 6
  6. 20 20 1

输出样例：

1040

多重背包问题的模板题 

  1. #include <iostream>
  2.  
  3. using namespace std;
  4.  
  5. const int N = 6010;
  6.  
  7. int n, m;
  8. int f[N];
  9.  
  10. int main()
  11. {
  12.     cin >> n >> m;
  13.     for(int i = 0; i < n; i ++ )
  14.     {
  15.         int v, w, s;
  16.         cin >> v >> w >> s;
  17.         for(int j = m; j >= 0; j -- )
  18.             for(int k = 0; k <= s && k * v <= j; k ++ )
  19.                 f[j] = max(f[j], f[j - k * v] + k * w);
  20.     }
  21.     
  22.     cout << f[m] << endl;
  23.     
  24.     return 0;
  25. }

AcWing 1023. 买书 

 

输入样例1：

20

输出样例1：

2

输入样例2：

15

输出样例2：

0

输入样例3：

0

输出样例3:

1

 

f[i,j]=f[i-1,j]+f[i,j-v]

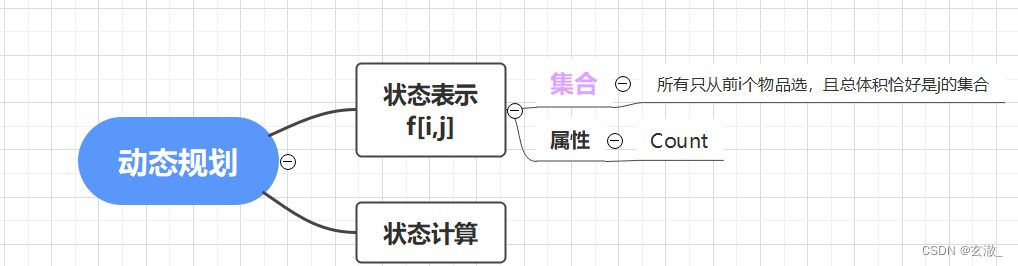
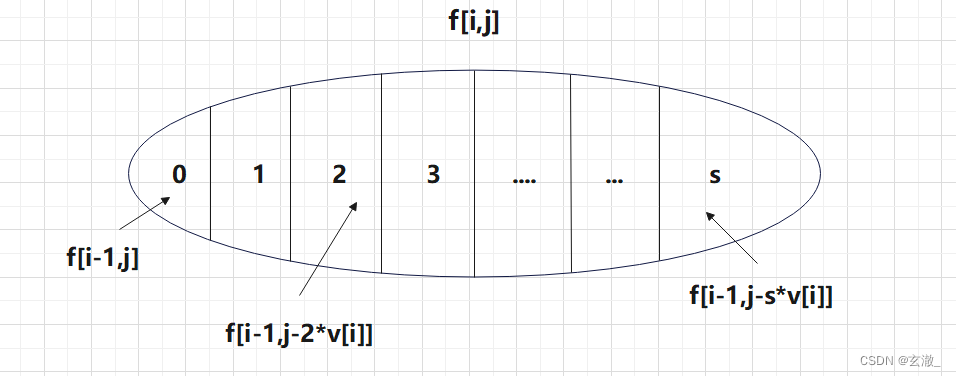
二维DP的朴素写法

  1. #include <iostream>
  2.  
  3. using namespace std;
  4.  
  5. const int N = 1010;
  6.  
  7. int v[5] = {0, 10, 20, 50, 100};
  8. int f[5][N];
  9.  
  10. int main()
  11. {
  12.     int m;
  13.     cin >> m;
  14.     
  15.     f[0][0] = 1;
  16.     for(int i = 1; i <= 4; i ++ )
  17.         for(int j = 0; j <= m; j ++ )
  18.         {
  19.             f[i][j] = f[i - 1][j];
  20.             if(j >= v[i]) f[i][j] += f[i][j - v[i]];
  21.         }
  22.     
  23.     cout << f[4][m] << endl;
  24.     
  25.     return 0;
  26. }

优化后的一维DP解法 

  1. #include <iostream>
  2.  
  3. using namespace std;
  4.  
  5. const int N = 1010;
  6.  
  7. int v[5] = {0, 10, 20, 50, 100};
  8. int f[N];
  9.  
  10. int main()
  11. {
  12.     int m;
  13.     cin >> m;
  14.     
  15.     f[0] = 1;
  16.     for(int i = 1; i <= 4; i ++ )
  17.         for(int j = v[i]; j <= m; j ++ )
  18.         {
  19.             f[j] += f[j - v[i]];
  20.         }
  21.     
  22.     cout << f[m] << endl;
  23.     
  24.     return 0;
  25. }

AcWing 12. 背包问题求具体方案

输入样例

  1. 4 5
  2. 1 2
  3. 2 4
  4. 3 4
  5. 4 6

输出样例：

1 4

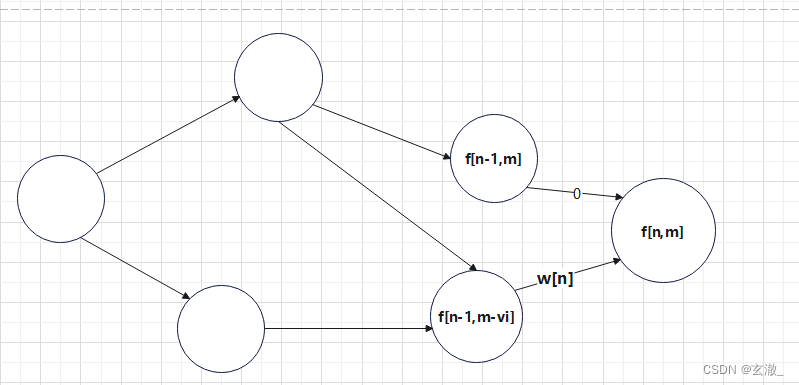
01背包问题的思路如下

其实是判断出每个物体是否被选

动态规划问题 -> 最短路问题（求路径问题）

  1. #include <iostream>
  2.  
  3. using namespace std;
  4.  
  5. const int N = 1010;
  6.  
  7. int n, m;
  8. int v[N], w[N];
  9. int f[N][N];
  10.  
  11. int main()
  12. {
  13.     cin >> n >> m;
  14.     for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
  16.     for (int i = n; i >= 1; i -- )
  17.         for (int j = 0; j <= m; j ++ )
  18.         {
  19.             f[i][j] = f[i + 1][j];
  20.             if (j >= v[i]) f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
  21.         }
  22.  
  23.     int j = m;
  24.     for (int i = 1; i <= n; i ++ )
  25.         if (j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i])
  26.         {
  27.             cout << i << ' ';
  28.             j -= v[i];
  29.         }
  30.  
  31.     return 0;
  32. }

AcWing 1013. 机器分配

 

输入样例：

  1. 3 3
  2. 30 40 50
  3. 20 30 50
  4. 20 25 30

输出样例：

  1. 70
  2. 1 1
  3. 2 1
  4. 3 1

这道题的本质上是一个分组背包问题+背包问题求具体方案

  1. #include <iostream>
  2. #include <algorithm>
  3.  
  4. using namespace std;
  5.  
  6. const int N = 11, M = 16;
  7.  
  8. int n, m;
  9. int w[N][M];
  10. int f[N][M];
  11. int way[N];
  12.  
  13. int main()
  14. {
  15.     cin >> n >> m;
  17.     for (int i = 1; i <= n; i ++ )
  18.         for (int j = 1; j <= m; j ++ )
  19.             cin >> w[i][j];
  21.     for (int i = 1; i <= n; i ++ )
  22.         for (int j = 0; j <= m; j ++ )
  23.             for (int k = 0; k <= j; k ++ )
  24.                 f[i][j] = max(f[i][j], f[i - 1][j - k] + w[i][k]);
  25.  
  26.     cout << f[n][m] << endl;
  27.  
  28.     int j = m;
  29.     for (int i = n; i; i -- )
  30.         for (int k = 0; k <= j; k ++ )
  31.             if (f[i][j] == f[i - 1][j - k] + w[i][k])
  32.             {
  33.                 way[i] = k;
  34.                 j -= k;
  35.                 break;
  36.             }
  37.  
  38.     for (int i = 1; i <= n; i ++ ) cout << i << ' ' << way[i] << endl;
  39.  
  40.     return 0;
  41. }

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/2023面试高手/article/detail/689960
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号