深度学习注意力机制（MHA）的训练（Eigen）_深度学习mha

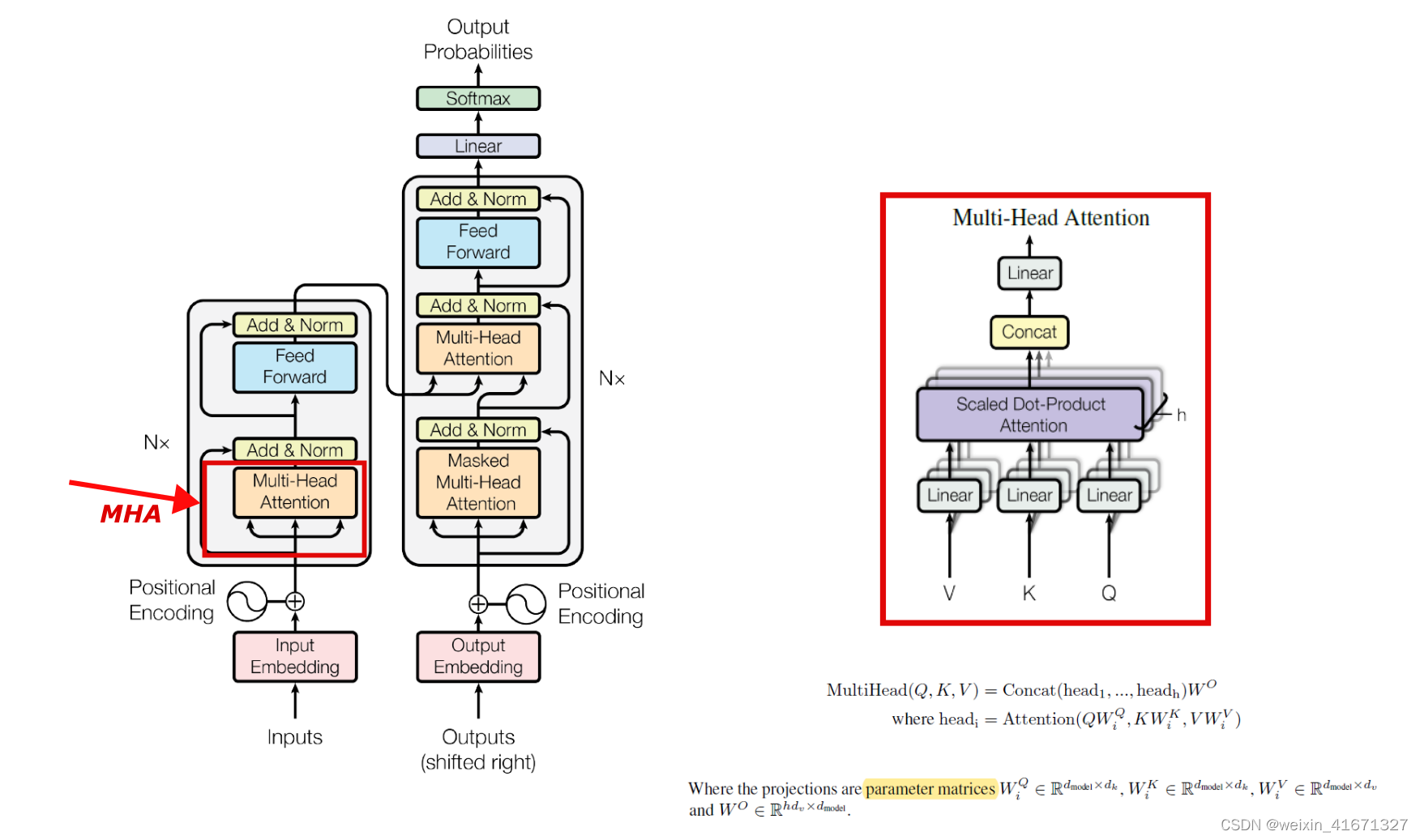
简介

本文使用Eigen3在Transformer模型中实现多头注意力的前向传播和反向传播。具体来说，这个eigenMHA (eigenDNN)【源码：https://github.com/jundaf2/eigenMHA】所对应了大致如下的cuDNN的api的功能：

• cudnnCreateAttnDescriptor()
• cudnnSetAttnDescriptor()
• cudnnGetAttnDescriptor()
• cudnnDestroyAttnDescriptor()
• cudnnGetMultiHeadAttnBuffers()
• cudnnGetMultiHeadAttnWeights()
• cudnnMultiHeadAttnForward()
• cudnnMultiHeadAttnBackwardData()
• cudnnMultiHeadAttnBackwardWeights()

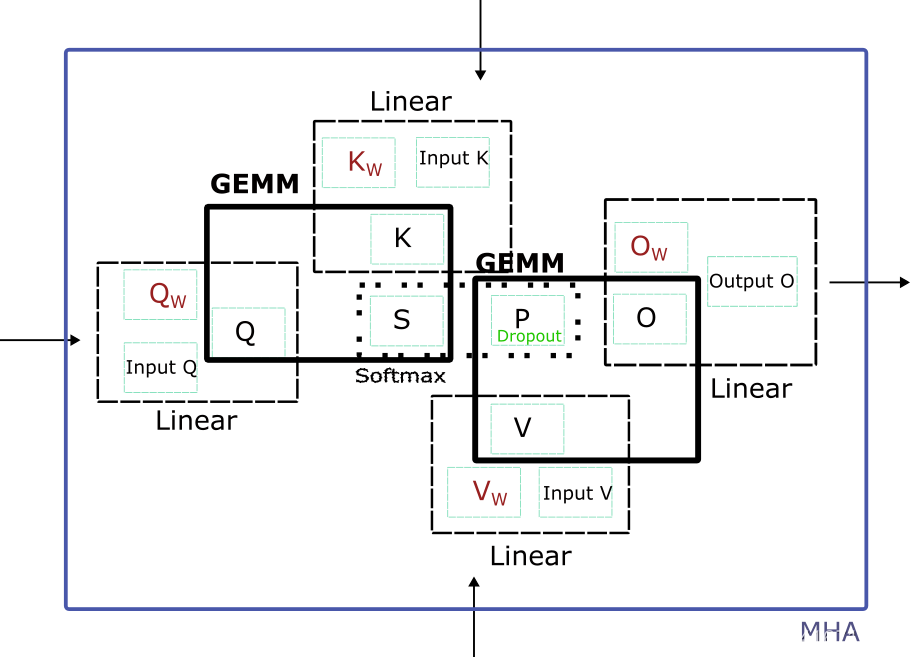
简单来说，MHA作为Tranformer模型中的一个模块，在训练中既要在需要将embedding，通过Q K V的线性层、S=Q*K^T（GEMM）、P=Softmax(Mask(S))、P=Dropout(P)、O=P*V（GEMM）、O的线性层 前向传播到下一层（可能是Layernorm），然后再在反向传播中，将输出O的梯度，通过O的线性层、O=P*V（GEMM）、P=Dropout(P)、P=Softmax(S)、S=Q*K^T（GEMM）、Q K V的线性层反向传播回输入端（embedding的梯度）。

MHA训练过程涉及到的变量

MHA训练前向

1. 输入QKV线性层的embeddings (前向起始点)

$${\mathbf{Q}}_{in}{\mathbf{K}}_{in}{\mathbf{V}}_{in}$$

2. 线性层权重和偏置

$${\mathbf{W}}_Q{\mathbf{b}}_Q$$

$${\mathbf{W}}_K{\mathbf{b}}_K$$

$${\mathbf{W}}_V{\mathbf{b}}_V$$

$${\mathbf{W}}_O{\mathbf{b}}_O$$

3. 计算中间变量
4. O的线性层输出值 和 目标值

$${\mathbf{O}}_{out}{\mathbf{O}}_{target}$$

MHA前向传播公式如下:

$$\mathbf{Q}={\mathbf{Q}}_{in}\ast {\mathbf{W}}_Q+{\mathbf{b}}_Q$$

$$\mathbf{K}={\mathbf{K}}_{in}\ast {\mathbf{W}}_K+{\mathbf{b}}_K$$

$$\mathbf{V}={\mathbf{V}}_{in}\ast {\mathbf{W}}_V+{\mathbf{b}}_V$$

$$\mathbf{S}=\mathbf{Q}\ast {\mathbf{K}}^T$$

KaTeX parse error: Undefined control sequence: \bfrac at position 42: …ask(\mathbf{S}*\̲b̲f̲r̲a̲c̲{1}{\sqrt{d}}))…

$$\mathbf{P}=DropoutFWD(\mathbf{P})$$

$$\mathbf{O}=\mathbf{P}\ast \mathbf{V}$$

$${\mathbf{O}}_{out}=\mathbf{O}\ast {\mathbf{W}}_O+{\mathbf{b}}_O$$

MSE Loss

在这个训练的计算结构中，反向传播的起始点是损失函数，因为我们仅仅关注于MHA本身，因此将MHA的输出${\mathbf{O}}_{out}$和预设的目标${\mathbf{O}}_{target}$输入MSE函数取得误差$loss$和反向传播的梯度 $${grad\_O}_{out}$$ 。
$$loss=MSELoss({\mathbf{O}}_{out},{\mathbf{O}}_{target})$$

MHA训练反向

1. MHA输出（O的线性层输出）的梯度 (来自于 LayerNorm，反向起始点)

$${grad\_O}_{out}$$

2. 中间变量的梯度
3. 输入的梯度

$${grad\_Q}_{in}{grad\_K}_{in}{grad\_V}_{in}$$

4. 权重和偏置的梯度

$${grad\_W}_Q{grad\_b}_Q$$

$${grad\_W}_K{grad\_b}_K$$

$${grad\_W}_V{grad\_b}_V$$

$${grad\_W}_O{grad\_b}_O$$

MHA反向传播公式如下:

$$grad\_O={grad\_O}_{out}\ast {\mathbf{W}}_O$$

$${grad\_W}_O={grad\_O}_{out}^T\ast \mathbf{O}$$

$${grad\_b}_O=colsum({grad\_O}_{out})$$

$$grad\_P=grad\_O\ast {\mathbf{V}}^T$$

$$grad\_V={\mathbf{P}}^T\ast grad\_O$$

$$grad\_P=DropoutBWD(grad\_P)$$

$$grad\_S=SoftmaxBWD(\mathbf{P},grad\_P)\ast \frac{1}{\sqrt{d}}$$

$$grad\_Q=grad\_S\ast \mathbf{K}$$

$$grad\_K={grad\_S}^T\ast \mathbf{Q}$$

$${grad\_Q}_{in}=grad\_Q\ast {\mathbf{W}}_Q$$

$${grad\_W}_Q={grad\_Q}^T\ast {\mathbf{Q}}_{in}$$

$${grad\_b}_Q=colsum(grad\_Q)$$

$${grad\_K}_{in}=grad\_K\ast {\mathbf{W}}_K$$

$${grad\_W}_K={grad\_K}^T\ast {\mathbf{K}}_{in}$$

$${grad\_b}_K=colsum(grad\_K)$$

$${grad\_V}_{in}=grad\_V\ast {\mathbf{W}}_V$$

$${grad\_W}_V={grad\_V}^T\ast {\mathbf{V}}_{in}$$

$${grad\_b}_V=colsum(grad\_V)$$

MHA训练库的组成部分

MSE损失函数

损失函数作为深度学习系统的起源，产生了损失量和回传梯度，是深度学习系统的基本组成部分。

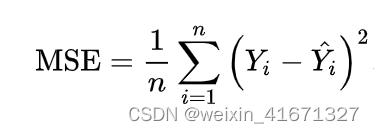
eidnnStatus_t eidnnMSELoss(
    eidnnHandle_t handle,
    const Tensor<float, 3> &output, 
    const Tensor<float, 3> &target,
    Tensor<float, 0> &loss,
    Tensor<float, 3> &d_loss);
1
2
3
4
5
6

线性层

cuDNN 没有给线性层操作提供了专门的API

在eigenDNN, 我们有

eidnnStatus_t eidnnLinearForward(eidnnHandle_t handle,
                    const Tensor<float, 3>& x, // data
                    const Tensor<float, 2>& w, // weight
                    const Tensor<float, 1>& bias, // bias
                    Tensor<float, 3>& y);

eidnnStatus_t eidnnLinearBackward(eidnnHandle_t handle,
                     const Tensor<float, 3>& dy,
                     const Tensor<float, 3>& x,
                     const Tensor<float, 2>& w,
                     Tensor<float, 3>& dx, // gradient of input data
                     Tensor<float, 2>& dw, // accumulated gradient of weight
                     Tensor<float, 1>& dbias // accumulated gradient of bias
                     );
1
2
3
4
5
6
7
8
9
10
11
12
13
14

批量矩阵乘法

$$C=\beta \ast C+\alpha \ast O{p}_c(MatMul(O{p}_a(A),O{p}_b(B)))$$

, 其中 $O{p}_m(M)$ 是对 $M$ 是否采取转置操作.

cuDNN 没有给批量矩阵乘法操作提供了专门的API

在eigenDNN, 我们有

eidnnStatus_t eidnnStridedBatchedGemmForward(
    eidnnHandle_t handle,
    float alpha,
    float beta,
    bool trans_A, // Op_a
    bool trans_B, // Op_b
    bool trans_C, // Op_c
    const Tensor<float, 4> &A, 
    const Tensor<float, 4> &B, 
    Tensor<float, 4> &C);
1
2
3
4
5
6
7
8
9
10

eidnnStatus_t eidnnStridedBatchedGemmBackward(
    eidnnHandle_t handle,
    float alpha,
    float beta,
    bool trans_A, // Op_a
    bool trans_B, // Op_b
    bool trans_C, // Op_c
    const Tensor<float, 4> &A, // A
    const Tensor<float, 4> &B, // B
    const Tensor<float, 4> &d_C, // gradient of C
    Tensor<float, 4> &d_A, // gradient of A
    Tensor<float, 4> &d_B // gradient of B
    );
1
2
3
4
5
6
7
8
9
10
11
12
13

Softmax

cuDNN 给softmax 操作提供了如下 API.

• cudnnSoftmaxForward()
• cudnnSoftmaxBackward()

在eigenDNN, 我们有

eidnnStatus_t eidnnSoftmaxForward(eidnnHandle_t handle,
                    eidnnSoftmaxAlgorithm_t algo,
                    eidnnSoftmaxMode_t mode,
                    const Tensor<float, 4>& x,
                    Tensor<float, 4>& y);
1
2
3
4
5

eidnnStatus_t eidnnSoftmaxBackward(eidnnHandle_t handle,
                     eidnnSoftmaxAlgorithm_t algo,
                     eidnnSoftmaxMode_t mode,
                     const Tensor<float, 4>& y,
                     const Tensor<float, 4>& dy,
                     Tensor<float, 4>& dx);
1
2
3
4
5
6

Dropout

cuDNN 给dropout 操作提供了如下 API.

• cudnnCreateDropoutDescriptor()
• cudnnDestroyDropoutDescriptor()
• cudnnDropoutGetStatesSize()
• cudnnDropoutGetReserveSpaceSize()
• cudnnDropoutForward()
• cudnnGetDropoutDescriptor()
• cudnnRestoreDropoutDescriptor()
• cudnnSetDropoutDescriptor()
• cudnnDropoutBackward()

在eigenDNN, 我们有

// dropout rate, 
// pointer to memory space of states (allocated by forward pass), 
// size of memory space in bytes (calculated by forward pass), 
// random seed
using eidnnDropoutDescriptor_t = std::tuple<float, void*, size_t, unsigned long long>; 
1
2
3
4
5

eidnnStatus_t eidnnDropoutForward(
    eidnnHandle_t                       handle,
    eidnnDropoutDescriptor_t      &dropoutDesc,
    const Tensor<float, 4>         &x, // input data
    Tensor<float, 4>               &y // input data after dropout
    );
1
2
3
4
5
6

eidnnStatus_t eidnnDropoutBackward(
    eidnnHandle_t                   handle,
    const eidnnDropoutDescriptor_t  dropoutDesc,
    const Tensor<float, 4>       &dy, // gradient of dropout output data
    Tensor<float, 4>             &dx // gradient of dropout input data
    );
1
2
3
4
5
6

Please star this project [https://github.com/jundaf2/eigenMHA] if you find it useful~