梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景：一个人被困在山上，需要从山上下来(i.e. 找到山的最低点，也就是山谷)。但此时山上的浓雾很大，导致可视度很低。因此，下山的路径就无法确定，他必须利用自己周围的信息去找到下山的路径。这个时候，他就可以利用梯度下降算法来帮助自己下山。具体来说就是，以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着山的高度下降的地方走，同理，如果我们的目标是上山，也就是爬到山顶，那么此时应该是朝着最陡峭的方向往上走。然后每走一段距离，都反复采用同一个方法，最后就能成功的抵达山谷。

我们同时可以假设这座山最陡峭的地方是无法通过肉眼立马观察出来的，而是需要一个复杂的工具来测量，同时，这个人此时正好拥有测量出最陡峭方向的能力。所以，此人每走一段距离，都需要一段时间来测量所在位置最陡峭的方向，这是比较耗时的。那么为了在太阳下山之前到达山底，就要尽可能的减少测量方向的次数。这是一个两难的选择，如果测量的频繁，可以保证下山的方向是绝对正确的，但又非常耗时，如果测量的过少，又有偏离轨道的风险。所以需要找到一个合适的测量方向的频率，来确保下山的方向不错误，同时又不至于耗时太多！

梯度下降是一阶迭代优化算法。为了使用梯度下降找到函数的局部最小值，一个步骤与当前位置的函数的梯度（或近似梯度）的负值成正比。如果相反，一个步骤与梯度的正数成比例，则接近该函数的局部较大值;该程序随后被称为梯度上升。梯度下降也被称为最陡峭的下降，或最快下降的方法。

1.2 梯度下降

首先，我们有一个可微分的函数。这个函数就代表着一座山。我们的目标就是找到这个函数的最小值，也就是山底。根据之前的场景假设，最快的下山的方式就是找到当前位置最陡峭的方向，然后沿着此方向向下走，对应到函数中，就是找到给定点的梯度，然后朝着梯度相反的方向，就能让函数值下降的最快！因为梯度的方向就是函数之变化最快的方向(在后面会详细解释)
所以，我们重复利用这个方法，反复求取梯度，最后就能到达局部的最小值，这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向，也就是场景中测量方向的手段。那么为什么梯度的方向就是最陡峭的方向呢？接下来，我们从微分开始讲起。

1.2.1 微分：

看待微分的意义，可以有不同的角度，最常用的两种是：

函数图像中，某点的切线的斜率
函数的变化率

几个微分的例子：

上面的例子都是单变量的微分，当一个函数有多个变量的时候，就有了多变量的微分，即分别对每个变量进行求微分：

1.2.2 梯度

梯度实际上就是多变量微分的一般化。例如：

我们可以看到，梯度就是分别对每个变量进行微分，然后用逗号分割开，梯度是用<>包括起来，说明梯度其实一个向量。

梯度是微积分中一个很重要的概念，之前提到过梯度的意义

在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率
在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向

这也就说明了为什么我们需要千方百计的求取梯度！我们需要到达山底，就需要在每一步观测到此时最陡峭的地方，梯度就恰巧告诉了我们这个方向。梯度的方向是函数在给定点上升最快的方向，那么梯度的反方向就是函数在给定点下降最快的方向，这正是我们所需要的。所以我们只要沿着梯度的方向一直走，就能走到局部的最低点！

1.3 梯度下降算法的数学解释

下面开始从数学上解释梯度下降算法的计算过程和思想。

此公式的意义是：J是关于Θ的一个函数，我们当前所处的位置为Θ0点，要从这个点走到J的最小值点，也就是山底。首先我们先确定前进的方向，也就是梯度的反向，然后走一段距离的步长，也就是α，走完这个段步长，就到达了Θ1这个点！

下面就这个公式的几个常见的疑问：

1.3.1 α是什么含义

α在梯度下降算法中被称作为学习率或者步长，意味着我们可以通过α来控制每一步走的距离，以保证不要步子跨的太大，不要走太快，错过了最低点。同时也要保证不要走的太慢，导致太阳下山了，还没有走到山下。所以α的选择在梯度下降法中往往是很重要的！α不能太大也不能太小，太小的话，可能导致迟迟走不到最低点，太大的话，会导致错过最低点！

1.3.2 为什么要梯度要乘以一个负号？

梯度前加一个负号，就意味着朝着梯度相反的方向前进！我们在前文提到，梯度的方向实际就是函数在此点上升最快的方向！而我们需要朝着下降最快的方向走，自然就是负的梯度的方向，所以此处需要加上负号。

1.3.3 用更数学的方式解释梯度下降法（为什么梯度的负方向是局部下降最快的方向？）

我们可以用泰勒公式表示损失函数，用更数学的方式解释梯度下降法：

迭代公式：
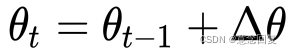
将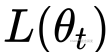在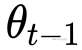处进行一阶泰勒展开：

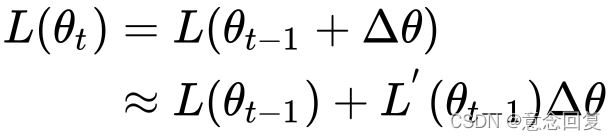
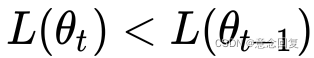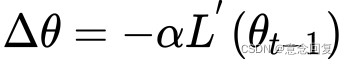要使得，可取：，则。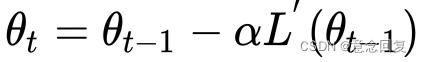

解释：要使得，可取：，如何推导？

，则我们可以得出：为函数值的变化量。我们要注意的是和均为向量，也就是两个向量进行点积，而向量进行点积的最大值，也就是两者共线的时候，也就是说的方向和方向相同的时候，点积值最大，这个点积值也代表了从点到点的上升量。

而正是代表函数值在处的梯度。前面又说明了的方向和方向相同的时候，点积值（变化值）最大，所以说明了梯度方向是函数局部上升最快的方向。也就证明了梯度的负方向是局部下降最快的方向。所以。这里的是步长，可通过line search确定，但一般直接赋一个小的数。

1.4 梯度下降算法的实例

我们已经基本了解了梯度下降算法的计算过程，那么我们就来看几个梯度下降算法的小实例，首先从单变量的函数开始。

1.4.1 单变量函数的梯度下降

我们假设有一个单变量的函数：

函数的微分：； 初始化，起点为； 学习率为，。

根据梯度下降的计算公式

开始进行梯度下降的迭代计算，经过四次的运算，也就是走了四步，基本就抵达了函数的最低点，也就是山底。

1.4.2 多变量函数的梯度下降

我们假设有一个目标函数

现在要通过梯度下降法计算这个函数的最小值。我们通过观察就能发现最小值其实就是 (0，0)点。接下来，我们会从梯度下降算法开始一步步计算到这个最小值！
假设初始的起点为：；初始的学习率为：；函数的梯度为：

进行多次迭代，已经基本靠近函数的最小值点：

1.5 python实现一个简单的梯度下降算法

1.5.1 原理

场景是一个简单的线性回归的例子：假设现在我们有一系列的点，如下图所示：

我们将用梯度下降法来拟合出这条直线！

首先，我们需要定义一个代价函数，在此我们选用均方误差代价函数

此共识中：

m是数据集中点的个数
½是一个常量，这样是为了在求梯度的时候，二次方乘下来就和这里的½抵消了，自然就没有多余的常数系数，方便后续的计算，同时对结果不会有影响
y 是数据集中每个点的真实y坐标的值
h 是我们的预测函数，根据每一个输入x，根据Θ 计算得到预测的y值，即

我们可以根据代价函数看到，代价函数中的变量有两个，所以是一个多变量的梯度下降问题，求解出代价函数的梯度，也就是分别对两个变量进行微分：

明确了代价函数和梯度，以及预测的函数形式。我们就可以开始编写代码了。但在这之前，需要说明一点，就是为了方便代码的编写，我们会将所有的公式都转换为矩阵的形式，python中计算矩阵是非常方便的，同时代码也会变得非常的简洁。

为了转换为矩阵的计算，我们观察到预测函数的形式：

我们有两个变量，为了对这个公式进行矩阵化，我们可以给每一个点 x 增加一维，这一维的值固定为1，这一维将会乘到Θ0上。这样就方便我们统一矩阵化的计算。

然后我们将代价函数和梯度转化为矩阵向量相乘的形式：

1.5.2 Python实现


# -*- coding: utf-8 -*-
import numpy as np
 
# Size of the points dataset.
m = 20
 
# Points x-coordinate and dummy value (x0, x1).
X0 = np.ones((m, 1))
X1 = np.arange(1, m+1).reshape(m, 1)
X = np.hstack((X0, X1))
 
# Points y-coordinate
y = np.array([
    3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
    11, 13, 13, 16, 17, 18, 17, 19, 21
]).reshape(m, 1)
 
# The Learning Rate alpha.
alpha = 0.01
 
def error_function(theta, X, y):
    '''Error function J definition.'''
    diff = np.dot(X, theta) - y
    return (1./2*m) * np.dot(np.transpose(diff), diff)
 
def gradient_function(theta, X, y):
    '''Gradient of the function J definition.'''
    diff = np.dot(X, theta) - y
    return (1./m) * np.dot(np.transpose(X), diff)
 
def gradient_descent(X, y, alpha):
    '''Perform gradient descent.'''
    theta = np.array([1, 1]).reshape(2, 1)
    gradient = gradient_function(theta, X, y)
    while not np.all(np.absolute(gradient) <= 1e-5):
        theta = theta - alpha * gradient
        gradient = gradient_function(theta, X, y)
    return theta
 
optimal = gradient_descent(X, y, alpha)
print('optimal:', optimal)
print('error function:', error_function(optimal, X, y)[0,0])

1.6 更一般的预测函数

1.6.1 变量形式

代价函数：

描述一下这个式子：

首先给定一个的矩阵

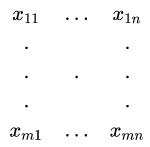
：表示需要求解的待定系数

：表示第 i 行所有的 x

：表示第 i 行所有的 x 乘以后的取值，即

，表示根据假设的模型计算的 y。

：表示第 i 行对应的真实的值

：表示令方差最小的函数（关于）

推导过程：

（1）0时，，即：

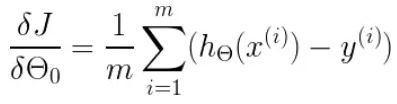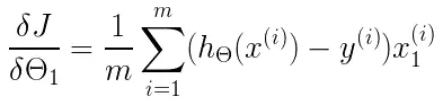（2）除0外，，即：

1.6.2 矩阵形式

给每一个点x增加一维，这一维的值固定为1，这一维将会乘到Θ0上。这样就方便我们统一矩阵化的计算。

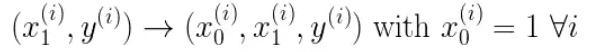
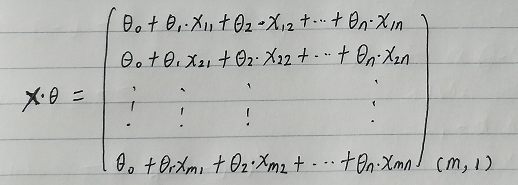
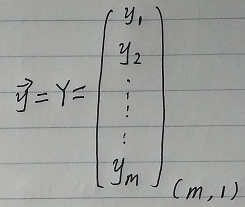
然后我们将代价函数和梯度转化为矩阵向量相乘的形式：

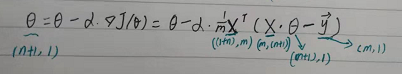
2 批量梯度下降法 BGD(Batch gradient descent)

2.1 简介

从 1.5 可以注意到，它得到的是一个全局最优解，但是每迭代一步，都要用到训练集所有的数据，如果m很大，那么可想而知这种方法的迭代速度会相当的慢。

　　对于批量梯度下降法，样本个数m，x为n维向量，一次迭代需要把m个样本全部带入计算，迭代一次计算量为m*n^2。

2.2 Python实现

x1和x2是样本值，y是预测目标，我们需要以一条直线来拟合上面的数据，待拟合的函数如下：

——1式

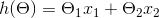
我们的目的就是要求出θ1和θ2的值，让h(θ)尽量逼近目标值y。

样本值取自于y=3*x1+4*x2

我们首先确定损失函数：

——2式

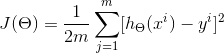
其中，J(θ)是损失函数，m代表每次取多少样本进行训练，如果采用SGD进行训练，那每次随机取一组样本，m=1；如果是批处理，则m等于每次抽取作为训练样本的数量。θ是参数，对应（1式）的θ1和θ2。求出了θ1和θ2，h(x)的表达式就出来了：

——3式

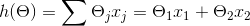
我们的目标是让损失函数J(θ)的值最小，根据梯度下降法，首先要用J(θ)对θ求偏导：

——4式

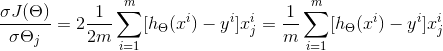
由于是要最小化损失函数（2式），所以参数θ按其负梯度方向来更新：

——5式

α是学习效率，即训练步长。


#-*- coding: utf-8 -*-
import random
#This is a sample to simulate a function y = theta1*x1 + theta2*x2
input_x = [[1,4], [2,5], [5,1], [4,2]]#输入
y = [19,26,19,20]   #输出
theta = [1,1]       #θ参数初始化
loss = 10           #loss先定义一个数，为了进入循环迭代
step_size = 0.001   #步长
eps =0.0001         #精度要求
max_iters = 10000   #最大迭代次数
error =0            #损失值
iter_count = 0      #当前迭代次数
while( loss > eps and iter_count < max_iters):
    loss = 0
    #这里更新权重的时候所有的样本点都用上了
    for i in range (4):   #4为样本数量
        pred_y = theta[0]*input_x[i][0]+theta[1]*input_x[i][1]
        theta[0] = theta[0] - step_size * (pred_y - y[i]) * input_x[i][0]
        theta[1] = theta[1] - step_size * (pred_y - y[i]) * input_x[i][1]
    for i in range (4):
        pred_y = theta[0]*input_x[i][0]+theta[1]*input_x[i][1]
        error = 0.5*(pred_y - y[i])**2
        loss = loss + error
    iter_count += 1
    print ('iters_count', iter_count)
 
print ('theta: ',theta )
print ('final loss: ', loss)
print ('iters: ', iter_count)

3 随机梯度下降 SGD（Stochastic gradient descent）

3.1 简介

每次迭代使用一组样本。针对BGD算法训练速度过慢的缺点，提出了SGD算法，普通的BGD算法是每次迭代把所有样本都过一遍。而SGD算法是从样本中随机抽出一组，训练后按梯度更新一次，然后再抽取一组，再更新一次，在样本量及其大的情况下，可能不用训练完所有的样本就可以获得一个损失值在可接受范围之内的模型了。

但由于每步接受的信息量有限，随机梯度下降法对梯度的估计常常出现偏差，造成目标函
数曲线收敛得很不稳定，伴有剧烈波动，有时甚至出现不收敛的情况。

最小化每条样本的损失函数，虽然不是每次迭代得到的损失函数都向着全局最优方向，但是大的整体的方向是向全局最优解的，最终的结果往往是在全局最优解附近，适用于大规模训练样本情况。

进一步地，有人会说深度学习中的优化问题本身就很难，有太多局部最优点的陷阱。没错，这些陷阱对随机梯度下降法和批量梯度下降法都是普遍存在的。但对随机梯度下降法来说，可怕的不是局部最优点，而是山谷和鞍点两类地形。山谷顾名思义就是狭长的山间小道，左右两边是峭壁；鞍点的形状像是一个马鞍，一个方向上两头翘，另一个方向上两头垂，而中心区域是一片近乎水平的平地。为什么随机梯度下降法最害怕遇上这两类地形呢？

在山谷中，准确的梯度方向是沿山道向下，稍有偏离就会撞向山壁，而粗糙的梯度估计使得它在两山壁间来回反弹震荡，不能沿山道方向迅速下降，导致收敛不稳定和收敛速度慢。
在鞍点处，随机梯度下降法会走入一片平坦之地（此时离最低点还很远，故也称plateau）。

想象一下蒙着双眼只凭借脚底感觉坡度，如果坡度很明显，那么基本能估计出下山的大致方向；如果坡度不明显，则很可能走错方向。同样，在梯度近乎为零的区域，随机梯度下降法无法准确察觉出梯度的微小变化，结果就停滞下来。

3.2 Python实现


# -*- coding:utf-8 -*-
# @author:sxy
 
import random
#This is a sample to simulate a function y = theta1*x1 + theta2*x2
input_x = [[1,4], [2,5], [5,1], [4,2]]#输入
y = [19,26,19,20]   #输出
theta = [1,1]       #θ参数初始化
loss = 10           #loss先定义一个数，为了进入循环迭代
step_size = 0.001   #步长
eps =0.0001         #精度要求
max_iters = 10000   #最大迭代次数
error =0            #损失值
iter_count = 0      #当前迭代次数
while( loss > eps and iter_count < max_iters):
    loss = 0
    #每一次选取随机的一个点进行权重的更新
    i = random.randint(0,3)
    pred_y = theta[0]*input_x[i][0]+theta[1]*input_x[i][1]
    theta[0] = theta[0] - step_size * (pred_y - y[i]) * input_x[i][0]
    theta[1] = theta[1] - step_size * (pred_y - y[i]) * input_x[i][1]
    for i in range (4):
        pred_y = theta[0]*input_x[i][0]+theta[1]*input_x[i][1]
        error = 0.5*(pred_y - y[i])**2
        loss = loss + error
    iter_count += 1
    print('iters_count', iter_count)
 
print('theta: ', theta)
print('final loss: ', loss)
print('iters: ', iter_count)

4 小批量梯度下降 MBGD（Mini-batch gradient descent）

4.1 简介

SGD相对来说要快很多，但是也有存在问题，由于单个样本的训练可能会带来很多噪声，使得SGD并不是每次迭代都向着整体最优化方向，因此在刚开始训练时可能收敛得很快，但是训练一段时间后就会变得很慢。在此基础上又提出了小批量梯度下降法，它是每次从样本中随机抽取一小批进行训练，而不是一组。

（ 1）如何选取参数m？在不同的应用中，最优的m通常会不一样，需要通过调参选取。一般m取2的幂次时能充分利用矩阵运算操作，所以可以在2的幂次中挑选最优的取值，例如32、 64、 128、 256等。
（2）如何挑选m个训练数据？为了避免数据的特定顺序给算法收敛带来的影响，一般会在每次遍历训练数据之前，先对所有的数据进行随机排序，然后在每次迭代时按顺序挑选m个训练数据直至遍历完所有的数据。
（3）如何选取学习速率α？为了加快收敛速率，同时提高求解精度，通常会采用衰减学习速率的方案：一开始算法采用较大的学习速率，当误差曲线进入平台期后，减小学习速率做更精细的调整。最优的学习速率方案也通常需要调参才能得到。

4.2 Python实现


# -*- coding:utf-8 -*-
# @author:sxy
import random
 
# This is a sample to simulate a function y = theta1*x1 + theta2*x2
input_x = [[1, 4], [2, 5], [5, 1], [4, 2]]
y = [19, 26, 19, 20]
theta = [1, 1]
loss = 10
step_size = 0.001
eps = 0.0001
max_iters = 10000
error = 0
iter_count = 0
while (loss > eps and iter_count < max_iters):
    loss = 0
 
    i = random.randint(0, 3)  # 注意这里，我这里批量每次选取的是2个样本点做更新，另一个点是随机点+1的相邻点
    j = (i + 1) % 4
    pred_y = theta[0] * input_x[i][0] + theta[1] * input_x[i][1]
    theta[0] = theta[0] - step_size * (pred_y - y[i]) * input_x[i][0]
    theta[1] = theta[1] - step_size * (pred_y - y[i]) * input_x[i][1]
 
    pred_y = theta[0] * input_x[j][0] + theta[1] * input_x[j][1]
    theta[0] = theta[0] - step_size * (pred_y - y[j]) * input_x[j][0]
    theta[1] = theta[1] - step_size * (pred_y - y[j]) * input_x[j][1]
    for i in range(4):
        pred_y = theta[0] * input_x[i][0] + theta[1] * input_x[i][1]
        error = 0.5 * (pred_y - y[i]) ** 2
        loss = loss + error
    iter_count += 1
    print('iters_count', iter_count)
 
print('theta: ', theta)
print('final loss: ', loss)
print('iters: ', iter_count)

5 梯度下降案例

多元线性回归算法，使用sklearn上的boston房价预测数据集，使用梯度下降法进行预测，其中，误差函数为


# -*- coding: utf-8 -*-
 
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
 
 
class LinearRegression:
    '''
    梯度下降法实现多元线性回归
    '''
 
    def __init__(self, alpha=0.001, times=1000, eps=0.01):
        '''
        :param alpha: 学习率，用来控制步长（权重调整幅度）
        :param times: 循环迭代的次数
        :param eps: 精度要求
        '''
        self.alpha = alpha
        self.times = times
        self.eps = eps
 
    def fit_DG(self, feature, target):
        '''
        使用梯度下降法进行训练
        '''
        mat_x0 = np.ones((len(feature),1))
        mat_xi = np.mat(feature)
        mat_x = np.hstack((mat_x0, mat_xi))
        mat_y = np.mat(target).T
        # 初始权重，权重向量初始值为0（或任何其他值），长度比X的特征数量多1（多出来的为截距）
        theta = np.zeros(mat_x.shape[1]).reshape(-1, 1)
        loss_list = []
        iter_count = 0
        loss = 10
        while(loss > self.eps and iter_count < self.times):
            # print(X.shape)
            # print(W[1:].shape)
            pred_y = np.dot(mat_x, theta)  # np.dot(),计算点积
            error = pred_y - mat_y  # 计算真实值与预测值之间的差距
            theta = theta - self.alpha * (mat_x.T * (pred_y-mat_y)) / mat_x.shape[1]
            error_square = np.square(error)
            loss = np.sum(error_square / (2 * mat_x.shape[1]))
            loss_list.append(loss)  # 将损失加入到损失列表中
            iter_count += 1
            print(iter_count)
            # loss = 0
        return theta
 
    def predict(self, feature, theta):
        mat_x0 = np.ones((len(feature), 1))
        mat_xi = np.array(feature)
        mat_x = np.hstack((mat_x0, mat_xi))
        result = np.dot(mat_x, theta)
        return result
 
 
def fit(feature):
    '''对给定的数据X，进行标准化处理。（将X的每一列都变成标准正太分布的数据）
    '''
    mat_x = np.array(feature)
    std = np.std(mat_x, axis=0)
    mean = np.std(mat_x, axis=0)
    mat_xs = (mat_x - mean)/std
    return mat_xs
 
def rmse(predict, test):
    MSE = np.sum(np.power((predict-test.reshape(-1, 1)), 2))/len(test)
    rmse = np.sqrt(mse)
    return rmse
 
def plot(test_feature, result):
    # 设置matplotlib 支持中文显示
    mpl.rcParams['font.family'] = 'SimHei'  # 设置字体为黑体
    mpl.rcParams['axes.unicode_minus'] = False  # 设置在中文字体是能够正常显示负号（“-”）
    plt.figure(figsize=(10,10))
    # 绘制预测值
    plt.plot(result, 'ro-', label="预测值")
    plt.plot(test_feature, 'go--', label="真实值")
    plt.xlabel("样本序号")
    plt.ylabel("房价")
    plt.title("线性回归预测-梯度下降法")
    plt.legend()
    plt.show()
 
 
if __name__ == "__main__":
    boston = datasets.load_boston()
    # train_feature, test_feature, train_target, test_target = train_test_split(
    #     boston.data, boston.target, test_size=0.3)
 
    # 进行标准化处理
    # data_feature = fit(boston.data)
    # train_feature, test_feature, train_target, test_target = train_test_split(
    #     data_feature, boston.target, test_size=0.3)
 
    # 进行标准化处理
    train_feature, test_feature, train_target, test_target = train_test_split(
        boston.data, boston.target, test_size=0.3)
    train_feature = fit(train_feature)
 
 
    lr = LinearRegression(0.00000001, 1000, 0.1)
    theta = lr.fit_DG(train_feature, train_target)
    print(theta)
    result = lr.predict(test_feature, theta)
    print(result)
    rmse_value = rmse(result, test_target)
    print(rmse_value)
    plot(test_target, result)

泰勒公式：

参考：批量梯度下降（BGD）、随机梯度下降（SGD）、小批量随机梯度下降（MSGD）实现过程详解_wzy的博客-CSDN博客_小批量随机梯度下降

梯度下降、随机梯度下降和批量梯度下降 - Hello~again - 博客园

[Math] 常见的几种最优化方法 - Poll的笔记 - 博客园

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/AllinToyou/article/detail/104005