机器学习：Gan（生成对抗网络）_生成对抗网络gan

版权声明：本文为CSDN博主「意念回复」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_39910711/article/details/123610198
版权声明：本文为CSDN博主「bashendixie5」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/bashendixie5/article/details/123602075

---

前言

生成式对抗网络（GAN, Generative Adversarial Networks ）是一种深度学习模型，是近年来复杂分布上无监督学习最具前景的方法之一。模型通过框架中（至少）两个模块：生成模型（Generative Model）和判别模型（Discriminative Model）的互相博弈学习产生相当好的输出。原始 GAN 理论中，并不要求 G 和 D 都是神经网络，只需要是能拟合相应生成和判别的函数即可。但实用中一般均使用深度神经网络作为 G 和 D 。一个优秀的GAN应用需要有良好的训练方法，否则可能由于神经网络模型的自由性而导致输出不理想。

---

1 原理简述

  生成对抗网络 (GAN) 是一类功能强大的神经网络，用于无监督学习。它是由 Ian J. Goodfellow 在 2014 年开发和引入的。GAN 基本上由两个相互竞争的神经网络模型组成的系统，它们相互竞争，能够分析、捕获和复制数据集中的变化。
  在 GAN 中，有一个生成器和一个鉴别器。生成器生成假数据样本（无论是图像、音频等）并试图欺骗鉴别器。另一方面，鉴别器试图区分真假样本。生成器和判别器都是神经网络，它们在训练阶段都相互竞争。重复这些步骤，在这个过程中，生成器和鉴别器在每次重复后在各自的工作中变得越来越好。

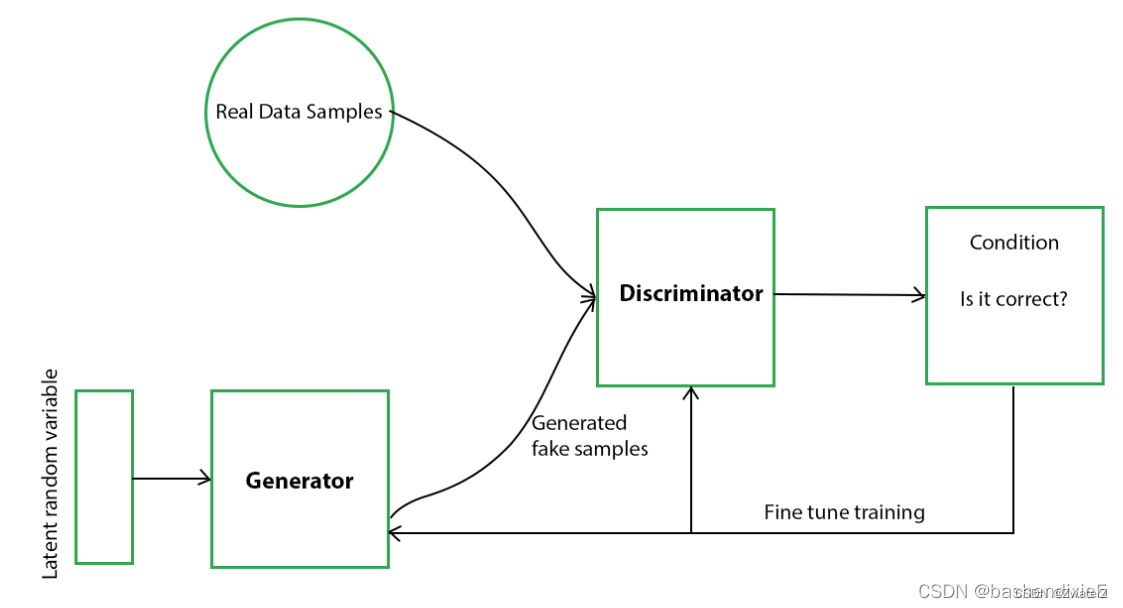
  生成模型捕获数据的分布，并以尝试最大化判别器出错的概率的方式进行训练。另一方面，判别器基于一个模型，该模型估计它获得的样本是从训练数据而不是从生成器接收的概率。GAN 被表述为一个极小极大游戏，其中判别器试图最小化其奖励V(D, G)，而生成器试图最小化判别器的奖励，或者换句话说，最大化其损失。它可以用以下公式在数学上描述。

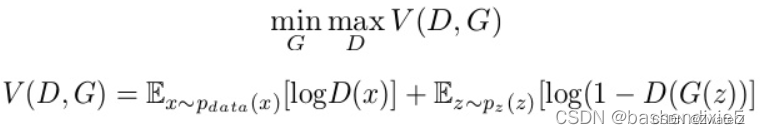
  其中，G = 生成器；D = 鉴别器；Pdata(x) = 真实数据的分布；P(z) = 生成器的分布；x = Pdata(x)的样本； z = P(z) 的样本；D(x) = 鉴别器网络；G( z) = 发电机网络。
  GAN 是一种通过将无监督问题视为有监督问题并同时使用生成模型和判别模型来自动训练生成模型的架构。
  GAN 为复杂的特定领域数据增强提供了途径，并为需要生成解决方案的问题提供了解决方案，例如图像到图像的转换。

---

  Ian J. Goodfellow等人于2014年10月在Generative Adversarial Networks中提出了一个通过对抗过程估计生成模型的新框架（Ian J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza.．Generative Adversarial Networks：Cornell University Library，2014）。框架中同时训练两个模型：捕获数据分布的生成模型G，和估计样本来自训练数据的概率的判别模型D。G的训练程序是将D错误的概率最大化。这个框架对应一个最大值集下限的双方对抗游戏。可以证明在任意函数G和D的空间中，存在唯一的解决方案，使得G重现训练数据分布，而D=0.5。在G和D由多层感知器定义的情况下，整个系统可以用反向传播进行训练。在训练或生成样本期间，不需要任何马尔可夫链或展开的近似推理网络。实验通过对生成的样品的定性和定量评估证明了本框架的潜力。

2 方法​​​​​​​​​​​​​​

  机器学习的模型可大体分为两类，生成模型（Generative Model）和判别模型（Discriminative Model）。判别模型需要输入变量 ，通过某种模型来预测 。生成模型是给定某种隐含信息，来随机产生观测数据。举个简单的例子：

• 判别模型：给定一张图，判断这张图里的动物是猫还是狗
• 生成模型：给一系列猫的图片，生成一张新的猫咪（不在数据集里）

  对于判别模型，损失函数是容易定义的，因为输出的目标相对简单。但对于生成模型，损失函数的定义就不是那么容易。我们对于生成结果的期望，往往是一个暧昧不清，难以数学公理化定义的范式。所以不妨把生成模型的回馈部分，交给判别模型处理。这就是Goodfellow他将机器学习中的两大类模型，Generative和Discrimitive给紧密地联合在了一起 。
  GAN的基本原理其实非常简单，这里以生成图片为例进行说明。假设我们有两个网络，G（Generator）和D（Discriminator）。正如它的名字所暗示的那样，它们的功能分别是：

• G是一个生成图片的网络，它接收一个随机的噪声z，通过这个噪声生成图片，记做G(z)。
• D是一个判别网络，判别一张图片是不是“真实的”。它的输入参数是x，x代表一张图片，输出D（x）代表x为真实图片的概率，如果为1，就代表100%是真实的图片，而输出为0，就代表不可能是真实的图片。
    在训练过程中，生成网络G的目标就是尽量生成真实的图片去欺骗判别网络D。而D的目标就是尽量把G生成的图片和真实的图片分别开来。这样，G和D构成了一个动态的“博弈过程”。
    最后博弈的结果是什么？在最理想的状态下，G可以生成足以“以假乱真”的图片G(z)。对于D来说，它难以判定G生成的图片究竟是不是真实的，因此D(G(z)) = 1。
    这样我们的目的就达成了：我们得到了一个生成式的模型G，它可以用来生成图片。
    Goodfellow从理论上证明了该算法的收敛性 ，以及在模型收敛时，生成数据具有和真实数据相同的分布（保证了模型效果）。

3 生成对抗网络

  GANs中生成模型和判别模型的选择没有强制限制，在Ian的论文中，判别模型D和生成模型G均采用多层感知机。GANs定义了一个噪声Pz(x) 作为先验，用于学习生成模型G在训练数据x上的概率分布Pg，G(z)表示将输入的噪声z映射成数据（例如生成图片）。D(x)代表x 来自于真实数据分布Pdata而不是Pg的概率。据此，优化的目标函数定义如下minmax的形式：

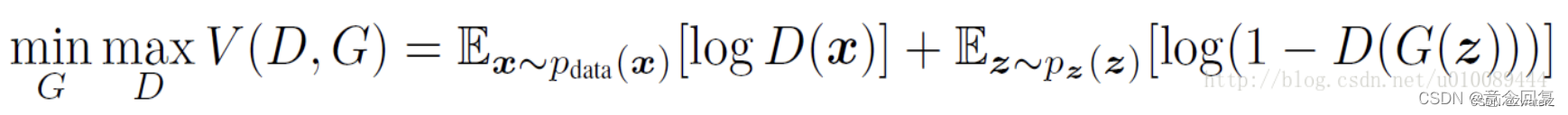
  原论文在参数的更新过程，是对D更新k次后，才对G更新1次。上式中的minmax可理解为当更新D时，需要最大化上式，而当更新G时，需要最小化上式，详细解释如下：
（1）在对判别模型D的参数进行更新时：

• 对于来自真实分布Pdata的样本x而言，我们希望D(x)的输出越接近于1越好，即logD(x)越大越好；
• 对于通过噪声z生成的数据G(z)而言，我们希望D(G(z))尽量接近于0（即D能够区分出真假数据），因此log(1−D(G(z)))也是越大越好，所以需要maxD。

（2）在对生成模型G的参数进行更新时：

  我们希望G(z)尽可能和真实数据一样，即Pg=Pdata。因此我们希望D(G(z))尽量接近于1，即log(1-D(G(z)))越小越好，所以需要minG。需要说明的是，logD(x)是与无关的项，在求导时直接为0。
  原论文中对GANs理论上的有效性进行了分析，即当固定G更新D时，最优解为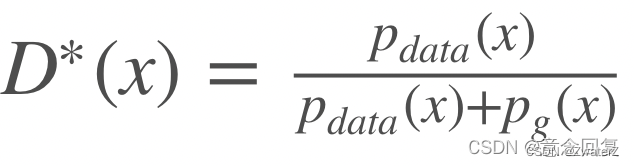
而在更新G时，目标函数取到全局最小值当且仅当。最后两个模型博弈的结果是G可以生成以假乱真的数据G(z)。而D难以判定G生成的数据是否真实，即D(G(z))=0.5。

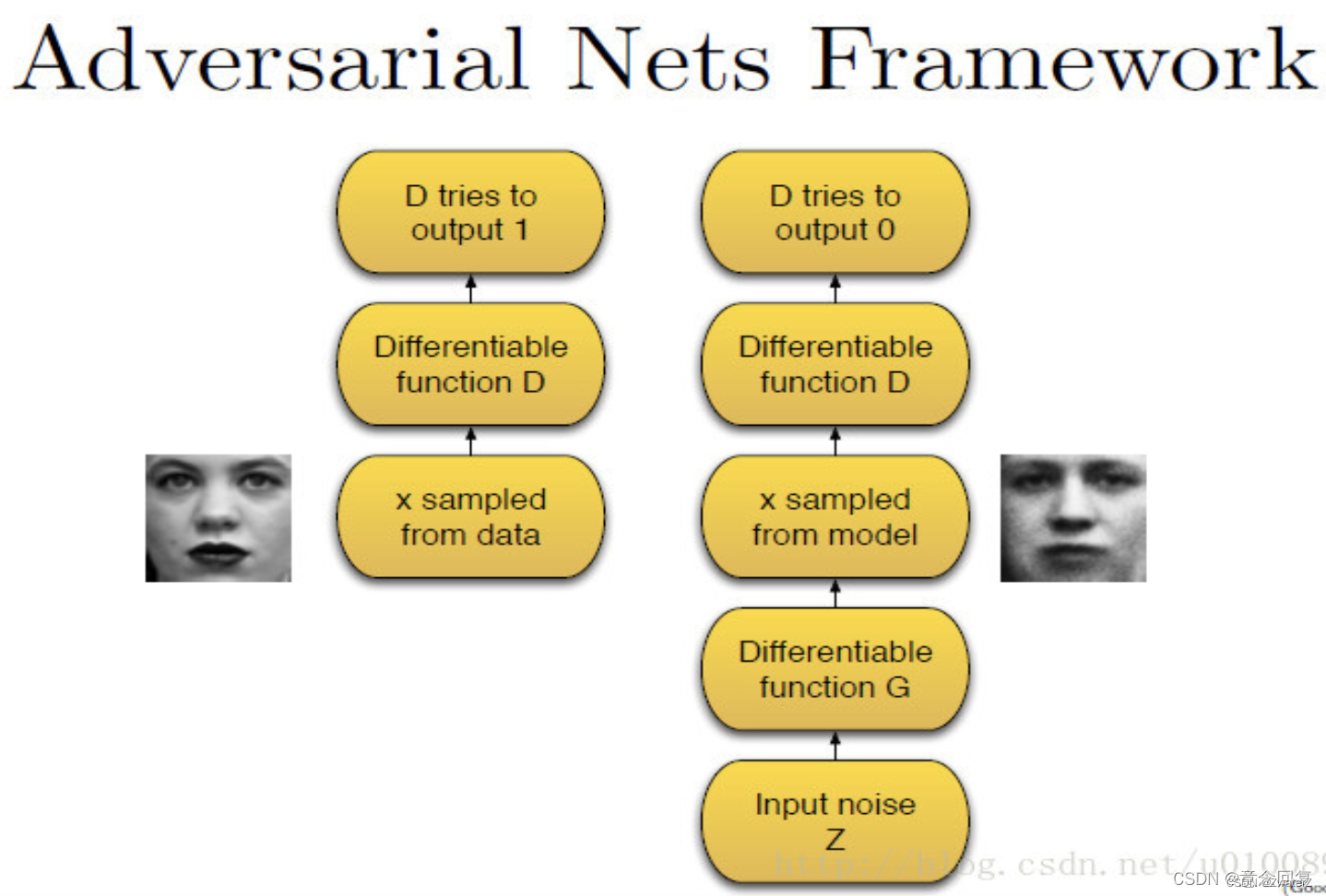
  第一阶段只有判别模型D参与。将训练集中的样本x作为D的输入，输出0-1之间的某个值，数值越大意味着样本x为真实数据的可能性越大。在这个过程中，我们希望D尽可能使输出的值逼近1。
  第二阶段中，判别模型D和生成模型G都参与，首先将噪声z输入G，G从真实数据集里学习概率分布并产生假的样本，然后将假的样本输入判别模型D，这一次D将尽可能输入数值0。所以在这个过程中，判别模型D相当于一个监督情况下的二分类器，数据要么归为1，要么归为0。

  下图给出了一个更为直观的解释：

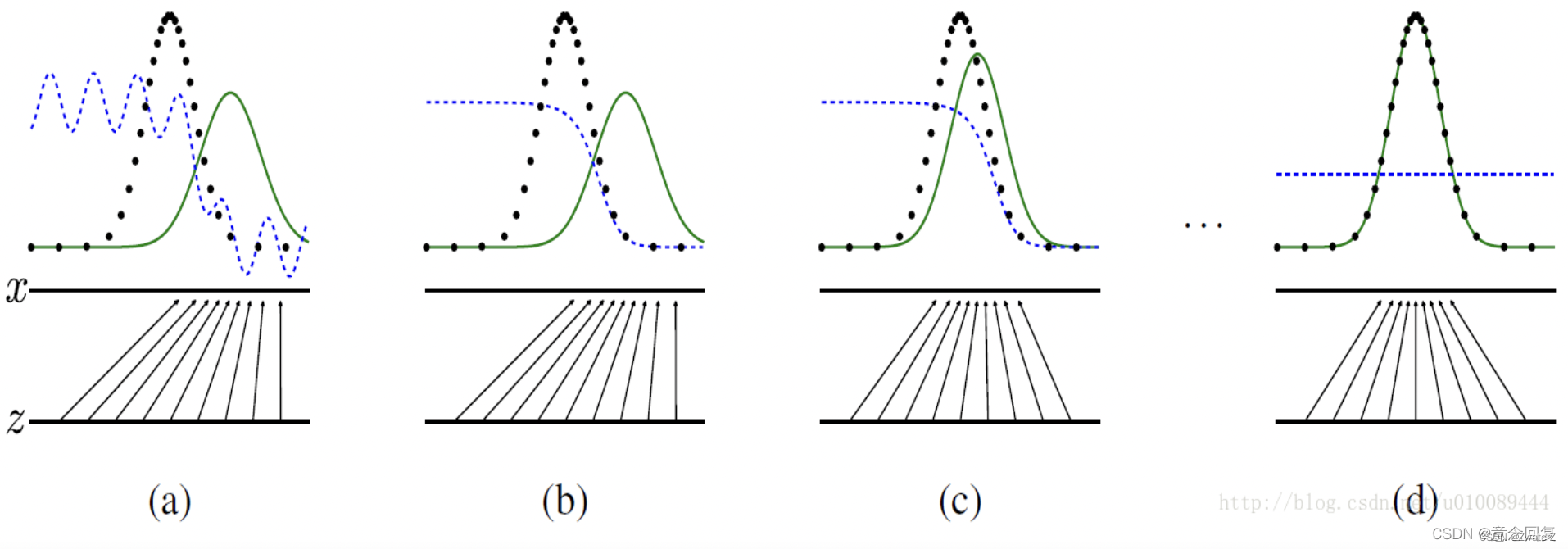
  其中，蓝色虚线为判别模型D的分布，黑色虚线为真实数据的分布Pdata，绿色实线为生成模型G学习的分布Pg。下方的水平线为均匀采样噪声z的区域，上方的水平线为数据x的区域。朝上的箭头表示将随机噪声转化成数据，即x=G(z)。
  从图（a）到图（b）给出了一个GANs的收敛过程。图(a)中Pg与Pdata存在相似性，但还未完全收敛，D是个部分准确的分类器。图(b)中，固定G更新D，收敛到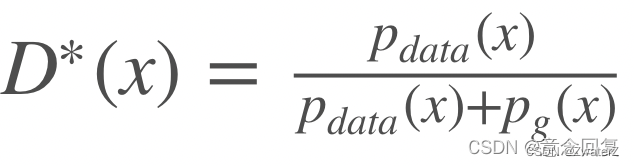

  图©中对G进行了1次更新，D的梯度引导G(z)移向更可能分类为真实数据的区域。图(d)中，训练若干步后，若G和D均有足够的capacity，它们接近某个稳定点，此时Pg=Pdata。判别模型将无法区分真实数据分布和生成数据分布，即D(x)=0.5。

论文中给出的算法流程如下：

4 应用

4.1 图像生成

  GAN最常使用的地方就是图像生成，如超分辨率任务，语义分割等等。

4.2 数据增强

  用GAN生成的图像来做数据增强，如图。

主要解决的问题是:

• 对于小数据集，数据量不足， 如果能生成一些就好了。
• 如果GAN生成了图片？怎么给这些数据label呢？因为他们相比原始数据也不属于预定义的类别。
  在（Gan参考资料）中，都做了一些尝试。实验想法也特别简单，先用原始数据（即使只有2000张图）训练一个GAN，然后生成图片，加入到训练集中。 总结一下就是：

1. GAN 生成数据是可以用在实际的图像问题上的（不仅仅是像mnist 这种toy dataset上work），作者在两个行人重识别数据集 和 一个细粒度识别 鸟识别数据集上都有提升。
2. GAN 数据有三种给pseudo label（伪标签）的方式， 假设我们做五分类

• 把生成的数据都当成新的一类, 六分类，那么生成图像的 label 就可以是 （0, 0, 0, 0, 0, 1） 这样给。
• 按照置信度最高的动态去分配，那个概率高就给谁 比如第三类概率高（0, 0, 1, 0, 0）
• 既然所有类都不是，那么可以参考inceptionv3，搞label smooth，每一类置信度相同（0.2, 0.2, 0.2, 0.2, 0.2） 注：作者16年12月写的代码，当时GAN效果没有那么好，用这个效果好也是可能的， 因为生成样本都不是很“真”，所以起到了正则作用。

5 GANs的改进

5.1 CGAN

  对抗网络的一个主要缺点是训练过程不稳定，为了提高训练的稳定性，文献（Mirza M, Osindero S. Conditional generative adversarial nets[J]. arXiv preprint arXiv:1411.1784, 2014.）提出了 Conditional Generative Adversarial Nets （CGAN），通过把无监督的 GAN 变成半监督或者有监督的模型，从而为 GAN 的训练加上一点目标，其优化的目标函数为：

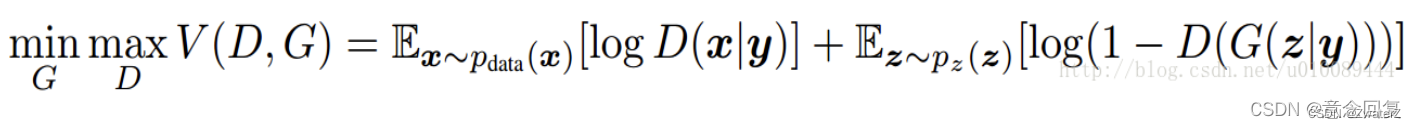
  CGAN在生成模型G和判别模型D的建模中均引入了条件变量 y，这里y可以是label或者其他数据形态，将y和GAN原有的输入合并成一个向量作为CGAN的输入。这个简单直接的改进被证明很有效，并广泛用于后续的相关工作中。CGAN模型的示意图如下所示：

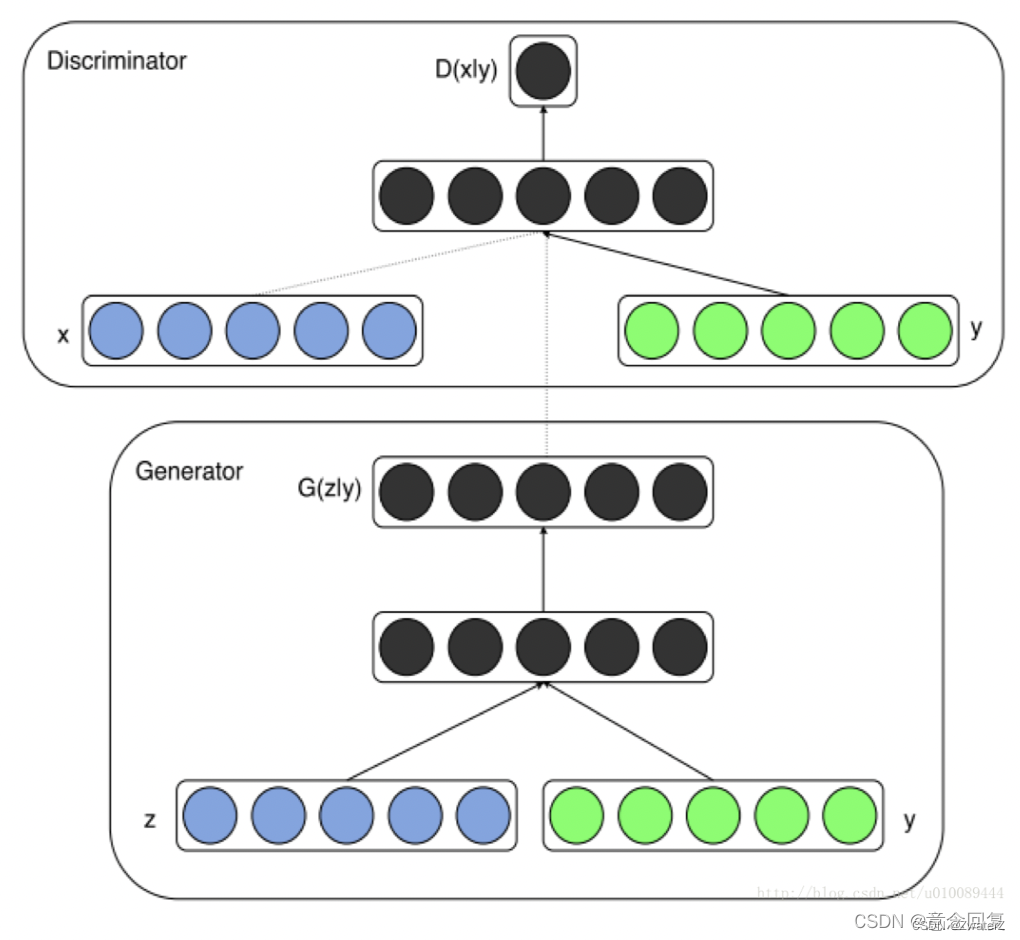
5.2 DCGAN

  文献（Radford A, Metz L, Chintala S. Unsupervised representation learning with deep convolutional generative adversarial networks[J]. arXiv preprint arXiv:1511.06434, 2015.）提出了一种Deep Convolutional Generative Adversarial Networks（DCGAN），将对抗网络与卷积神经网络相结合进行图片生成，DCGAN模型的结构如下：

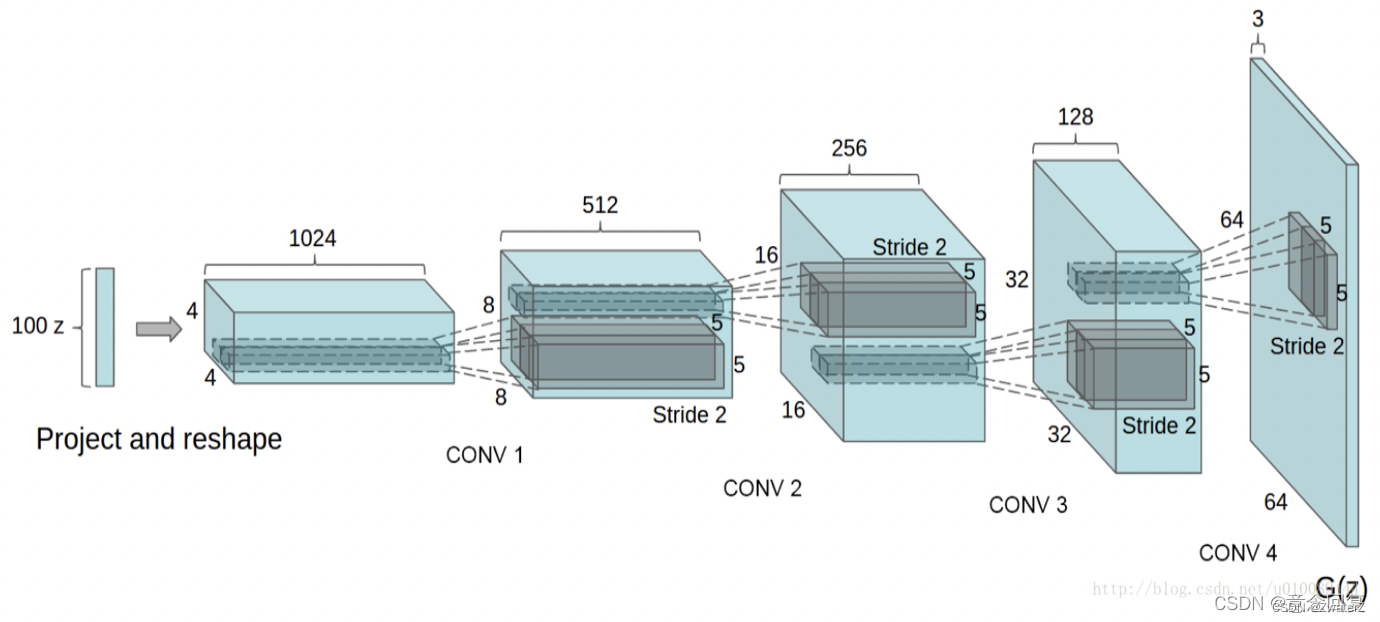
  DCGANs的基本架构就是使用几层“反卷积”（Deconvolution）。传统的CNN是将图像的尺寸压缩，变得越来越小，而反卷积是将初始输入的小数据（噪声）变得越来越大（但反卷积并不是CNN的逆向操作），例如在上面这张图中，从输入层的100维noise，到最后输出层64x64x3的图片，从小维度产生出大的维度。反卷积的示意图如下所示，2x2的输入图片，经过3x3 的卷积核，可产生4x4的feature map：

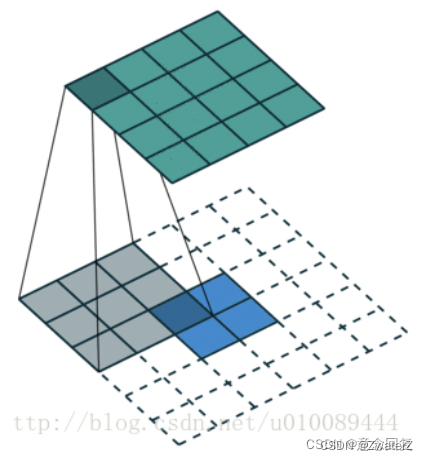
  由于反卷积存在于卷积的反向传播中。其中反向传播的卷积核矩阵是前向传播的转置，所以其又可称为transport convolution。只不过我们把反向传播的操作拿到了前向传播来做，就产生了所谓的反卷积一说。但是transport convolution只能还原信号的大小，不能还原其值，因此不是真正的逆操作。
DCGAN的另一个改进是对生成模型中池化层的处理，传统CNN使用池化层（max-pooling或mean-pooling）来压缩数据的尺寸。在反卷积过程中，数据的尺寸会变得越来越大，而max-pooling的过程并不可逆，所以DCGAN的论文里并没有采用池化的逆向操作，而只是让反卷积的滑动步长设定为2或更大值，从而让尺寸按我们的需求增大。另外，DCGAN模型在G和D上均使用了batch normalization，这使得训练过程更加稳定和可控。

  该文献将GANs应用于文本转图像（Text to Image），从而可根据特定输入文本所描述的内容来产生特定图像。因此，生成模型里除了输入随机噪声之外，还有一些特定的自然语言信息。所以判别模型不仅要区分样本是否是真实的，还要判定其是否与输入的语句信息相符。网络结构如下图所示：

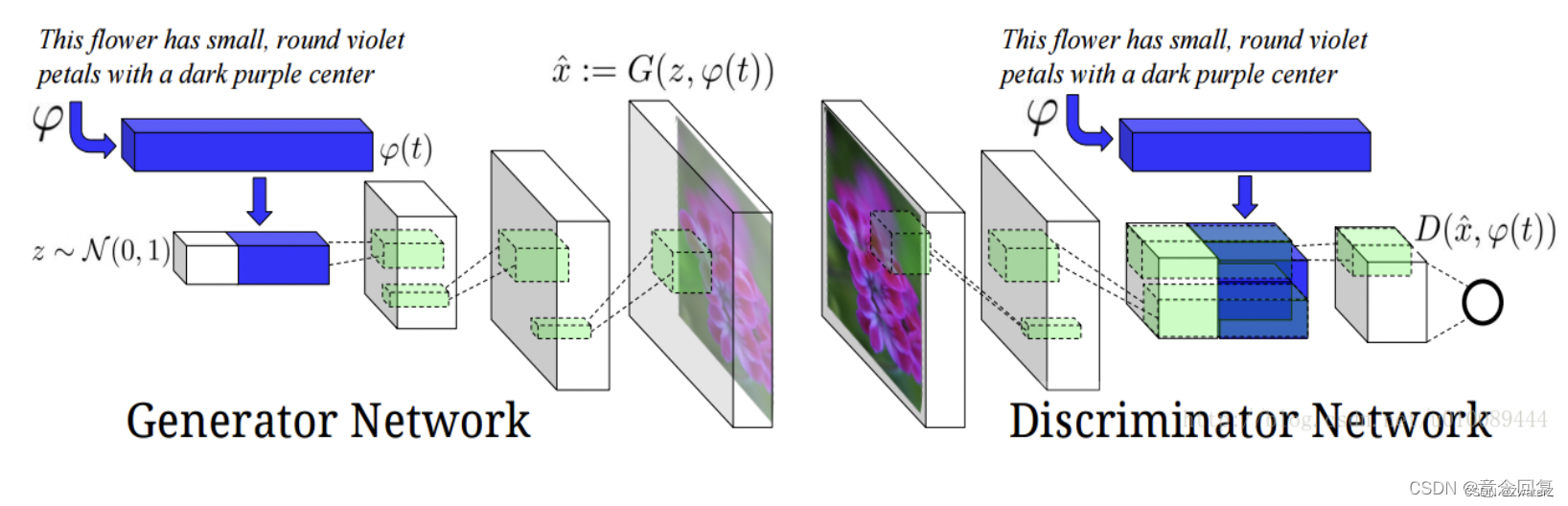
  以下是实验的结果，同时可看到模型仍然存在Mode Collapse（模式坍塌）的问题：

6 Mode Collapse

  什么是 mode collapse？为什么会发生 mode collapse？还是可以用这个图景来轻松解释。

  首先我们有一批样本 x1, x2, … , xn，我们希望能找到一个生成模型，这个模型有能力造出一批新的样本，我们希望这批新样本跟原样本很相似。怎么造呢？很简单，分两步走。

“挖坑”

  第一步，挖坑：我们挖很多坑，这些坑的分布可以用一个能量函数 U(x) 描述，然后我们要把真实样本 x1, x2, … , xn都放在坑底，然后把造出来的假样本放到“坑腰”：

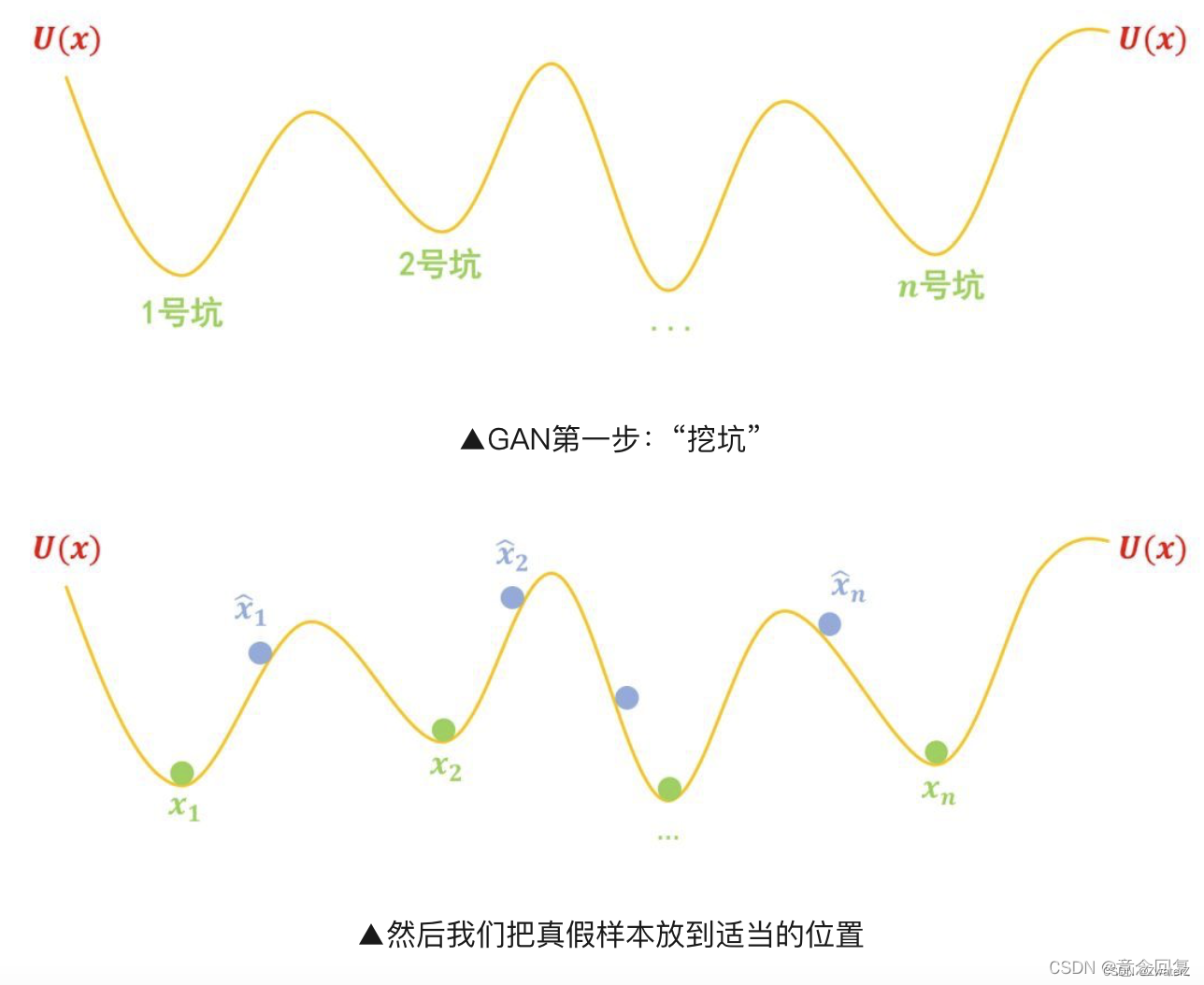
“跳坑”

  **第二步，跳坑：**把 U(x) 固定住，也就是不要再动坑了，然后把假样本松开，显然它们就慢慢从滚到坑底了，而坑底代表着真实样本，所以都变得很像真样本了：

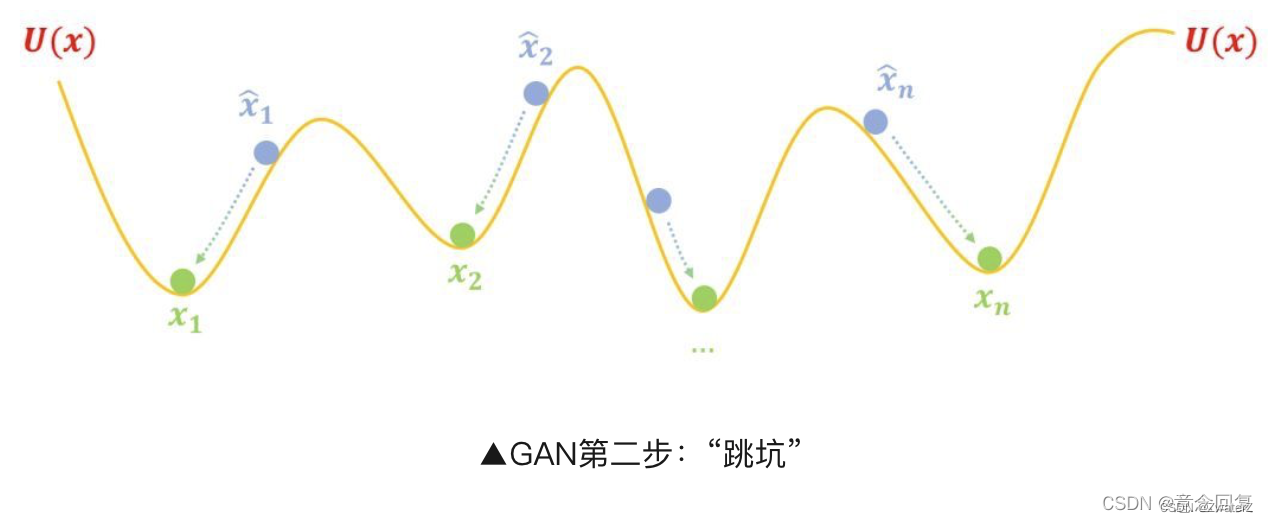
  前面我们画的图把假样本画得很合理，但是如果一旦初始化不好、优化不够合理等原因，使得同时聚在个别坑附近，比如：

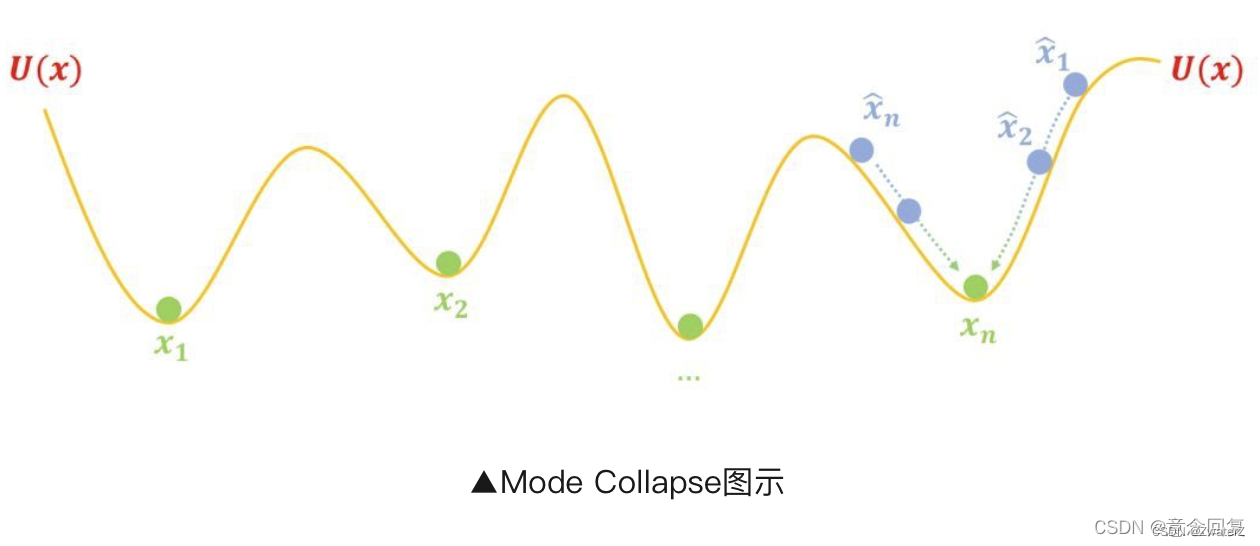
  这时候按照上述过程优化，所有假样本都都往 xn 奔了，所以模型只能生成单一（个别）样式的样本，这就是 mode collapse。
  简单来看，mode collapse 是因为假样本们太集中，不够“均匀”，所以我们可以往生成器那里加一个项，让假样本有均匀的趋势。这个项就是假样本的熵 H(X)=H(G(Z))，我们希望假样本的熵越大越好，这意味着越混乱、越均匀，所以生成器的目标可以改为：

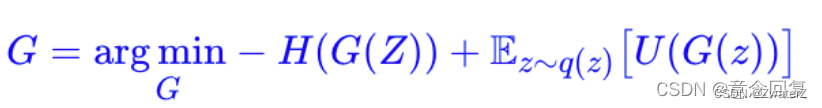
  这样理论上就能解决 mode collapse 的问题。