基于动态图卷积神经网络的脑电情绪识别_dreamer数据库

Abstract—In this paper, a multichannel EEG emotion recognition method based on a novel dynamical graph convolutional neural networks (DGCNN) is proposed. The basic idea of the proposed EEG emotion recognition method is to use a graph to model the multichannel EEG features and then perform EEG emotion classification based on this model. Different from the traditional graph convolutional neural networks (GCNN) methods, however, the proposed DGCNN method can dynamically learn the intrinsic relationship between different electroencephalogram (EEG) channels, represented by an adjacency matrix, via training a neural network so as to benefit for more discriminative EEG feature extraction. Then, the learned adjacency matrix is used for learning more discriminative features for improving the EEG emotion recognition. We conduct extensive experiments on the SJTU emotion EEG dataset (SEED) and DREAMER dataset. The experimental results demonstrate that the proposed method achieves better recognition performance than the state-of-the-art methods, in which the average recognition accuracy of 90.4% is achieved for subject dependent experiment while 79.95% for subject independent cross-validation one on the SEED database, and the average accuracies of 86.23%, 84.54% and 85.02% are respectively obtained for valence, arousal and dominance classifications on the DREAMER database.

摘要提出了一种基于新型动态图卷积神经网络(DGCNN)的多通道脑电信号情感识别方法。所提出的EEG情绪识别方法的基本思想是利用图对多通道EEG特征进行建模，然后根据该模型进行EEG情感分类。然而，与传统的图卷积网络 (GCNN) 方法不同，所提出的 DGCNN 方法可以通过训练神经网络来学习由邻接矩阵表示的不同脑电图 (EEG) 通道之间的内在关系，从而有利于更具辨别力的 EEG 特征提取。然后，利用学习到的邻接矩阵学习更多的判别特征来改进EEG情绪识别。我们对 SJTU 情绪 EEG 数据集 (SEED) 和 DREAMER 数据集进行了广泛的实验。实验结果表明，所提出的方法比最先进的方法实现了更好的识别性能，其中主题相关实验的平均识别准确率为 90.4%，主题独立交叉验证的平均识别准确率为 79.95%，SEED 数据库上的主题独立交叉验证的平均准确率分别为 86.23%、84.54% 和 85.02%，分别为 DREAMER 数据库上的效价、唤醒和优势分类。

Index Terms—EEG emotion recognition, adjacency matrix, graph convolutional neural networks (GCNN), dynamical convolutional neural networks (DGCNN)

索引术语-EEG情绪识别、邻接矩阵、图卷积网络(GCNN)、动态卷积神经网络(DGCNN)

I. INTRODUCTION

EMOTION recognition plays an important role in the human-machine interaction [1], which enables machine to perceive the emotional mental states of human beings so as to make machine more 'sympathetic' in the humanmachine interaction. Basically, emotion recognition methods can be divided into two categories. The first one is based on non-physiological signals, such as facial expression images [2][3][4][5], body gesture [6], and voice signal [7]. The second one is based on physiological signal, such as electroencephalogram (EEG) [8], electromyogram (EMG) [9], and electrocardiogram (ECG) [10]. Among the various types of physiological signals, EEG signal is one of the mostTengfei Song is with the Key Laboratory of Child Development and Learning Science (Southeast University), Ministry of Education, Southeast University, Nanjing 210096, China, and also with the School of Information Science and Engineering, Southeast University, Nanjing 210096, China. Wenming Zheng is with the Key Laboratory of Child Development and Learning Science (Southeast University), Ministry of Education, Southeast University, Nanjing 210096, China, and also with the School of Biological Science and Medical Engineering, Southeast University, Nanjing 210096, China. (E-mail: wenming zheng@seu.edu.cn). Peng Song is with the School of Computer and Control Engineering, Yantai University, Yantai, China, 264005. Zhen Cui is with the school of Computer Science, Nanjing University of Science and Technology, Nanjing, Jiangsu, P.R. China.commonly used ones, which is directly captured from the brain cortex and hence it would be advantageous to reflect the mental states of human beings. With the rapid development of dry EEG electrode techniques and the EEG-based signal processing methods, EEG based emotion recognition has received increasing applications in recent years [11][12][13][14].

情感识别在人机交互[1]中起着重要的作用，它使机器能够感知人类的情感心理状态，使机器在人机交互中更加“同情”。基本上，情感识别方法可以分为两类。第一个是基于非生理信号，如面部表情图像[2][3][4][5]、身体手势[6]和语音信号[7]。第二种是基于生理信号，如脑电图(EEG)[8]、肌电图(EMG)[9]和心电图(ECG)[10]。在各种类型的生理信号中，脑电信号是宋伟最大的方法之一，东南大学儿童发展与学习科学教育部重点实验室，南京210096，以及东南大学信息科学与工程学院，南京210096。郑文明就职于东南大学儿童发展与学习科学教育部重点实验室，南京210096，东南大学生物科学与医学工程学院，南京210096。（电子邮件：我们nming zeng@seu.edu.cn）。彭宋鹏就职于西安塔尼大学计算机与控制工程学院，中国264005。崔振就职于南京科技大学计算机科学学院，南京，江苏，P。R.中国。常用的直接从大脑皮层捕获，因此反映人类心理状态是有利的。随着干EEG电极技术和基于EEG的信号处理方法的快速发展，近年来基于EEG的情感识别受到越来越多的关注[11][12][13][14]。

Basically, there are two major ways to describe human's emotions [15], i.e., the discrete basic emotion description approach and the dimension approach. For the discrete basic emotion description approach, the emotions are classified into a set of discrete status, e.g., the six basic emotions (i.e., joy, sadness, surprise, fear, anger, and disgust) [16]. Different from the discrete emotion description approach, the dimension approach describes emotions in continuous form, in which the emotions are characterized by three dimensions (valence, arousal and dominance) [17][18] or simply two dimensions (valence and arousal), in which the valence dimension mainly characterizes how positive or negative the emotions are, whereas the arousal dimension aims to characterize the degree of how excited or apathetic the emotions are [15].

基本上，有两种主要的方法来描述人类的情绪[15]，即离散的基本情感描述方法和维度方法。对于离散的基本情感描述方法，情绪分为一组离散状态，例如六种基本情绪（即喜悦、悲伤、惊讶、恐惧、愤怒和厌恶）[16]。与离散情绪描述方法不同，维度方法以连续形式描述情绪，其中情绪的特征是三个维度（效价、唤醒和支配）[17][18]或简单的两个维度（效价和唤醒），其中效价维度主要表征情绪的积极或消极程度，而唤醒维度旨在表征情绪兴奋程度或同情程度[15]。

The research of applying EEG signal to the emotion recognition can be traced back to work of Musha et al. in [19]. During the past decades, many machine learning and signal processing methods are proposed to deal with the EEG emotion recognition [20][21]. A typical EEG emotion recognition method usually consists of two major parts, i.e., discriminative EEG feature extraction part and emotion classification part. Basically, the EEG features used for emotion recognition can be generally divided into two kinds, i.e., time-domain feature type and frequency-domain feature type. The time domain features, e.g., Hjorth feature [22], fractal dimension feature [23] and higher order crossing feature [24], mainly capture the temporal information of EEG signals. Different to the time-domain feature, however, the frequency-domain feature aims to capture the EEG emotion information from the frequency point of view. One of the most commonly used frequency-domain feature extraction methods is to decompose the EEG signal into several frequency bands, e.g., δ band (1-3Hz), θ band (4-7Hz), α band (8-13Hz), β band (14-30Hz) and γ band (31-50Hz) [20][25][26][27], and then extract EEG features from each frequency band, respectively. The commonly used EEG features include the differential entropy (DE) feature [28][29], the power spectral density (PSD) feature [30], the differential asymmetry (DASM) feature [23], the rational asymmetry (RASM) feature [31] and the differential caudality (DCAU) feature [18].

将脑电信号应用于情感识别的研究可以追溯到Musha等人在[19]中的工作。在过去的几十年里，人们提出了许多机器学习和信号处理方法来处理EEG情绪识别[20][21]。典型的EEG情绪识别方法通常由鉴别EEG特征提取部分和情感分类部分两大部分组成。基本上，用于情感识别的EEG特征一般可以分为两类，即时域特征类型和频域特征类型。时域特征，如hjorth特征[22]、分形维数特征[23]和高阶交叉特征[24]，主要捕获脑电信号的时间信息。然而，与时域特征不同，频域特征旨在从频率的角度捕获脑电图情感信息。最常用的频域特征提取方法之一是将脑电信号分解成几个频段，例如δ频段(1-3Hz)、θ频段(4-7Hz)、α频段(8-13Hz)、β频段(14-30Hz)和γ频段(31-50Hz)[20][25][26][27]，然后分别从每个频段提取EEG特征。常用的脑电特征包括微分熵(DE)特征[28][29]、功率谱密度(PSD)特征[30]、微分不对称性(DASM)特征[23]、理性不对称(RASM)特征[31]和差分尾度(DCAU)特征[18]。

To deal with EEG emotion classification problem, there are many methods appeared in the literatures [32], among which the method of using deep neural networks (DNN) [18] had been demonstrated to be one of the most successful one. Convolutional neural networks (CNN) is one of the most famous DNN approaches and had been widely used to cope with various classification problems, such as image classification [33][34][35][36], object detection [37], tracking [38] and segmentation [39]. Although CNN model had been demonstrated to be very powerful in dealing with the classification problems, it is notable that previous applications of CNN focus more on the local feature learning from image, video and speech, in which the data points of the signal are continuously changed. For another feature learning problems, such as the feature learning from transportation network and brain network, the traditional CNN method may not be well suitable because the signals are discrete and discontinuous in the spatial domain. In this case, graph based description methods [40][41] would provide more effective way.

为了处理EEG情感分类问题，文献[32]中出现了许多方法，使用深度神经网络(DNN)[18]的方法已被证明是最成功的方法之一。卷积神经网络(CNN)是最著名的DNN方法之一，已被广泛用于应对各种分类问题，如图像分类[33][34][35][36]，目标检测[37]，跟踪[38]和分割[39]。尽管 CNN 模型已被证明在处理分类问题方面非常强大，但值得注意的是，CNN 的先前应用更多地关注图像、视频和语音的局部特征学习，其中信号的数据点不断变化。对于另一个特征学习问题，例如交通网络和大脑网络的特征学习，传统的 CNN 方法可能不太适合，因为信号在空间域是离散的和不连续的。在这种情况下，基于图的描述方法[40][41]将提供更有效的方法

Graph neural networks (GNN) [42] aims to build the neural networks under the graph theory to cope with the data in graph domain. Graph convolutional neural networks (GCNN) [43] is an extension of the traditional CNN method by combining CNN with spectral theory [44]. Compared with classical CNN method, GCNN would be more advantageous in dealing with the discriminative feature extraction of signals in the discrete spatial domain [45]. More importantly, the GCNN method provides an effective way to describe the intrinsic relationship between different nodes of the graph, which would provide a potential way to explore the relationships among the multiple EEG channels during the EEG emotion recognition.

图神经网络(GNN)[42]旨在建立图论下的神经网络，以应对图域中的数据。图卷积网络(GCNN)[43]是将CNN与谱理论[44]相结合，是传统CNN方法的扩展。与经典的CNN方法相比，GCNN在处理离散空间域[45]中信号的鉴别特征提取方面更有利。更重要的是，GCNN方法提供了一种有效的方法来描述图不同节点之间的内在关系，这为探索EEG情绪识别过程中多个EEG通道之间的关系提供了一种潜在的方法。

Motivated by the success of the GCNN model, in this paper we will investigate the multichannel EEG emotion recognition problem via graph representation approach, in which each EEG channel corresponds to a vertex node whereas the connection between two different vertex nodes corresponds to an edge of the graph. Although GCNN can be used to describe the connections among different nodes according to their spatial positions, we should predetermine the connections among the various EEG channels before applying it to build the emotion recognition model. On the other hand, it is notable that the spatial position connections among the EEG channels are different from the functional connections among them. In other words, a closer spatial relationship may not guarantee a closer functional relationship, whereas the functional relationship would be useful for the discriminative EEG feature extraction in emotion recognition. Consequently, it is not reasonable to predetermine the connections of the graph nodes according to their spatial positions.

受 GCNN 模型成功的启发，在本文中，我们将通过图表示方法研究多通道 EEG 情感识别问题，其中每个 EEG 通道对应一个顶点节点，而两个不同顶点节点之间的连接对应于图的边。虽然 GCNN 可用于根据其空间位置描述不同节点之间的连接，但我们应该在应用各种 EEG 通道之间建立情感识别模型之前预先确定各种 EEG 通道之间的连接。另一方面，值得注意的是，EEG通道之间的空间位置连接与它们之间的功能连接不同。换句话说，更紧密的空间关系可能无法保证更紧密的函数关系，而函数关系将有助于情感识别中的判别脑电图特征提取。因此，根据图节点的空间位置预先确定图节点的连接是不合理的。

To alleviate the limitations of the GCNN method, in this paper we propose a novel dynamical graph convolutional neural networks (DGCNN) model for learning discriminative EEG features as well as the intrinsic relationship, e.g., the functional relationship, among the various EEG channels. Specifically, to learn the relationships among the various EEG channels, we propose a novel method to construct the connections among the various vertex nodes of the graph by learning an adjacency matrix.

为了缓解 GCNN 方法的局限性，本文提出了一种新的动态图卷积神经网络 (DGCNN) 模型来学习各种 EEG 通道之间的判别 EEG 特征以及内在关系，例如函数关系。具体来说，为了学习各种脑电通道之间的关系，我们提出了一种新的方法，通过学习邻接矩阵来构造图的各个顶点节点之间的连接。

However, different from the traditional GCNN method that predetermines the adjacency matrix before the model training, the proposed DGCNN method learns the adjacency matrix in a dynamic way, i.e., the entries of the adjacency matrix are adaptively updated with the changes of graph model parameters during the model training. Consequently, in contrast to the GCNN method, the adjacency matrix learned by the DGCNN would be more useful because it captures the intrinsic connections of the EEG channels and hence it would be able to improve the discriminant abilities of the networks.

然而，与传统的在模型训练之前预先确定邻接矩阵的GCNN方法不同，DGCNN方法动态学习邻接矩阵，即邻接矩阵的条目随着模型训练过程中图模型参数的变化自适应地更新。因此，与 GCNN 方法相比，DGCNN 学习的邻接矩阵将更有用，因为它捕获了 EEG 通道的内在连接，因此它能够提高网络的判别能力。

The remainder of this paper is organized as follows: In section II, we will briefly review the preliminaries of graph theory. In section III, we will propose the DGCNN model and the EEG emotion recognition method based on this model. Extensive experiments are conducted in section IV. Finally, we conclude the paper in section V.

本文的其余部分安排如下：在第二节中，我们将简要回顾图论的初步内容。在第三节中，我们将提出了基于该模型的DGCNN模型和EEG情感识别方法。广泛的实验在第四节中进行。最后，我们在第 V 节中总结了论文。

II. GRAPH PRELIMINARY

In this section, we will introduce some preliminary knowledge about the graph representation and the spectral graph filtering, which are the basis for our DGCNN method.

在本节中，我们将介绍一些关于图表示和谱图过滤的初步知识，这是我们DGCNN方法的基础。

A. Gragh Representation

A directed and connected graph can be defined as G ={V, E, W }, in which V represents the set of nodes with the number of |V| = N and E denotes the set of edges connecting these nodes. Let W ∈ RN ×N denote an adjacency matrix describing the connections between any two nodes in V, in which the entry of W in the i-th row and j-th column, denoted by wij , measures the importance of the connection between the i-th node and the j-th one. Fig.1 illustrates an example of a graph containing six vertex nodes and the edges connecting the nodes of the graph, as well as the adjacency matrix associated with the graph, where the different color arrows in the lefthand side of the figure denote the edges connecting the source nodes to destination nodes, whereas the right-hand side of the figure is the illustration of the corresponding adjacency matrix.

有向图和连通图可以定义为 G ={V, E, W }，其中 V 表示节点数为 |V| = N 的节点集，E 表示连接这些节点的边集。令 W ∈ RN ×N 表示描述 V 中任意两个节点之间的连接的邻接矩阵，其中 W 在第 i 行和第 j 列的条目，用 wij 表示，测量第 i 个节点和第 j 个节点之间的连接的重要性。图1示出了包含六个顶点节点和连接图的节点的边的图的示例，以及与图相关联的邻接矩阵，其中图左侧的不同颜色箭头表示连接源节点到目标节点的边，而图的右侧是相应邻接矩阵的图示。

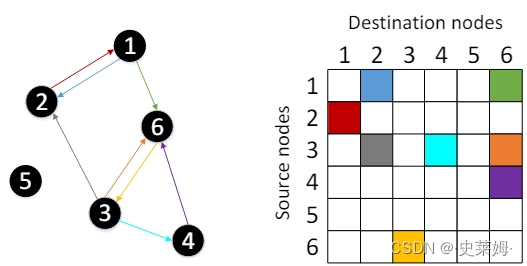
Fig. 1. Example of a directed graph and the corresponding adjacency matrix, where the left part is the connections of six nodes and right part is the adjacency matrix.

图 1. 有向图的示例和相应的邻接矩阵，其中左侧是六个节点的连接，右侧部分是邻接矩阵。

The commonly used methods to determine the entries wijof the adjacency matrix W include the distance function method [46] and K-nearest neighbor (KNN) rule method [47]. A typical distance function would be the Gaussian kernel function, which can be expressed as:

确定邻接矩阵W的条目wij的常用方法包括距离函数方法[46]和k近邻(KNN)规则方法[47]。典型的距离函数是高斯核函数，可以表示为：

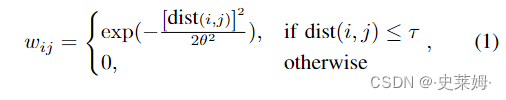
where τ and θ are two parameters to be fixed, dist(i, j) denotes the distance between the i-th node and the j-th one.

其中 τ 和 θ 是要固定的两个参数，dist(i, j) 表示第 i 个节点和第 j 个节点之间的距离。

B. Spectral Graph Filtering

The spectral graph theory has been successfully used for building expander graphs [48], spectral clustering [49], graph visualization [50] and other applications [51]. Spectral graph filtering, also called graph convolution, is a popular signal processing method for graph data operation, in which graph fourier transform (GFT) [46] is a typical example. Let L denote the Laplacian matrix of the graph G. Then, Lcan be expressed as

谱图理论已成功应用于构建扩展图[48]、谱聚类[49]、图可视化[50]等应用[51]。光谱图滤波，也称为图卷积，是一种流行的图数据操作信号处理方法，其中图傅里叶变换(GFT)[46]是典型的例子。令 L 表示图 G 的拉普拉斯矩阵。然后，L可以表示为

where D ∈ RN ×N is a diagonal matrix and the i-th diagonal element can be calculated by Dii = ∑j wij . For a given spatial signal x ∈ RN , its GFT is expressed as follows:

其中 D ∈ RN ×N 是一个对角矩阵，第 i 个对角元素可以通过 Dii = ∑j wij 计算。对于给定的空间信号 x ∈ RN ，其 GFT 表示如下：

where ˆx denotes the transformed signal in the frequency domain, U is an orthonormal matrix that can be obtained via the singular value decomposition (SVD) of the graph Laplacian matrix L [44]:

其中 ^x 表示频域中的变换信号，U 是可以通过图拉普拉斯矩阵 L [44] 的奇异值分解 (SVD) 获得的正交矩阵：

in which the columns of U = [u0, · · · , uN −1] ∈ RN ×Nconstitute the Fourier basis, and Λ = diag([λ0, · · · , λN −1])is a diagonal matrix.

其中 U = [u0, · · · , uN -1] ∈ RN ×N 的列构成傅里叶基，Λ = diag([λ0, · · · , λN -1]) 是一个对角矩阵。

From (3), we can obtain that the inverse of GFT can be expressed as the following form:

从（3）中，我们可以得到GFT的逆可以表示为以下形式：

Then, the definition of convolution of two signal x and y on the graph ∗G can be expressed as [43]:

然后，图∗G上两个信号x和y的卷积定义可以表示为[43]：

where denotes the element-wise Hadamard product. Now let g(·) be a filtering function such that a signal xfiltered by g(L) can be expressed as:

其中表示逐元素 Hadamard 乘积。现在让 g(·) 是一个过滤函数，使得由 g(L) 过滤的信号 x 可以表示为：

where g(Λ) is expressed as

其中 g(Λ) 表示为

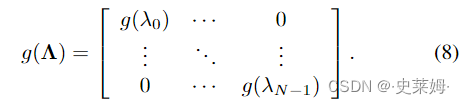
It is notable that the filtering operation of (7) is equivalent to the graph convolution of the signal x with the vector ofUg(Λ) due to the following formulation:

值得注意的是，(7)的滤波操作等价于信号x与ug(Λ)的向量的图卷积，公式如下:

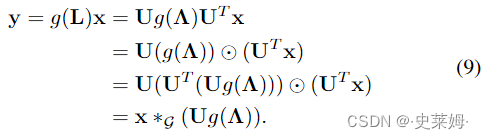
III. DGCNN FOR EEG EMOTION RECOGNITION

In this section, we will firstly propose the DGCNN model and then apply it to the EEG emotion recognition problem, in which the adjacency matrix W that characterizes the relationships of the various vertex nodes is dynamically learned instead of being predetermined [43].

在本节中，我们将首先提出DGCNN模型，并将其应用于EEG情绪识别问题，其中动态学习表征不同顶点节点之间关系的邻接矩阵W，而不是预先确定的[43]。

A. DGCNN Model for EEG Emotion Recognition

Let W∗ denote the optimal adjacency matrix to be learned. Then, the graph convolution of the signal x with the vector of U∗g(Λ∗) defined by the spatial filtering g(L∗) can be expressed as:

令 W∗ 表示要学习的最优邻接矩阵。然后，信号x与空间滤波g(L∗)定义的U∗g(Λ∗)的向量的图卷积可以表示为：

where the L∗ can be calculated from W∗ based on (2), andΛ∗ = diag([λ∗0, · · · , λ∗N −1]) is a diagonal matrix. Since it is difficult to directly calculate the expression ofg(Λ∗), we simplify this calculation by using the polynomial expansion of g(Λ∗), e.g., using the K order Chebyshev polynomials [43], to replace it, such that the calculation becomes much easier and faster. Specifically, let λ∗max denote the largest element among the diagonal entries of Λ∗ and denote the normalized Λ∗ by  ̃Λ∗ = 2Λ∗/λ∗max − IN , such that the diagonal elements of  ̃Λ∗ lie in the interval of [−1, 1], whereIN is the N × N identity matrix. Under the K order Chebyshev polynomials framework, we obtain that g(Λ∗) can be approximated by:

其中 L∗ 可以根据 (2) 从 W∗ 计算，Λ∗ = diag([λ∗0,····,λ∗N -1]) 是一个对角矩阵。由于很难直接计算g(Λ *)的表达式，我们通过使用g(Λ *)的多项式展开来简化这个计算，例如，使用K阶切比雪夫多项式[43]来代替它，这样计算就变得更加容易和更快。具体来说，设 λ∗max 表示 Λ∗ 的对角线条目中的最大元素，并用 ̃Λ∗ = 2Λ∗/λ∗max − IN 表示归一化 Λ∗，使得 ̃Λ∗ 的对角元素位于 [−1, 1] 的区间内，其中 IN 是 N × N 单位矩阵。在K阶切比雪夫多项式框架下，我们得到g(Λ *)可以近似为:

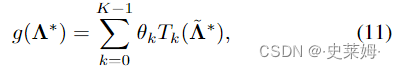
where θk is the coefficient of Chebyshev polynomials, andTk(x) can be recursively calculated according to the following recursive expressions:

其中 θk 是切比雪夫多项式的系数，Tk(x) 可以根据以下递归表达式递归计算：

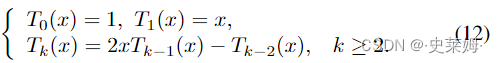
According to (11), we obtain the graph convolution operation defined in (10) can be rewritten by:

根据（11），我们得到（10）中定义的图卷积操作可以改写为：

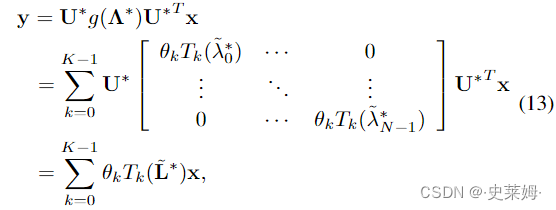
The expression of (13) means that calculating the graph convolution of x can be expressed as the combination of the convolutional results of x with each of the Chebyshev polynomial components. Based on the expression of (13), we proposed the DGCNN model for EEG emotion recognition. The framework of the proposed method is illustrated in Fig.2, which consists of four major layers, i.e., the graph filtering layer, the convolutional layer, the Relu activation layer, and the full connection layer.

(13)的表达式意味着计算x的图卷积可以表示为x的卷积结果与每个切比雪夫多项式分量的组合。基于(13)的表达，我们提出了DGCNN模型进行脑电信号情感识别。该方法框架如图2所示，它由图滤波层、卷积层、Relu激活层和全连接层四个主要层组成。

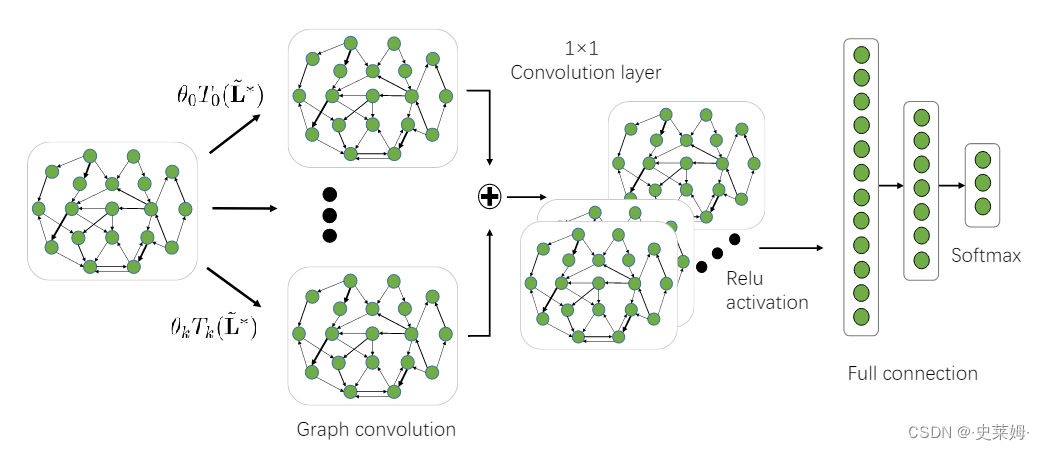
Fig. 2. The framework of the DGCNN model for EEG emotion recognition, which consists of the graph convolutional operation via the learned graph connections, convolution layer with 1 × 1 kernel, relu activation and the full connection. The inputs of the model are the EEG features extracted from multiple frequency bands, e.g., five frequency bands (δ band, θ band, α band, β band, and γ band), in which each EEG channel is represented as a node of the graph. The outputs are the predicted labels through softmax.

图2所示。DGCNN模型用于EEG情感识别的框架，该框架由通过学习的图连接、1×1核的卷积层、RELU激活和全连接组成。该模型的输入是从多个频段提取的EEG特征，例如五个频段(δ频段、θ频段、α频段、β频段和γ频段)，其中每个EEG通道被表示为图的节点。输出是通过 softmax 的预测标签。

Specifically, the input of the DGCNN model corresponds to the EEG features extracted from multiple frequency bands, e.g., five frequency bands (δ band, θ band, α band, β band, and γ band), in which each EEG channel is represented as a node in the DGCNN model. Following the graph filtering operation is a 1 × 1 convolution layer, which aims to learn the discriminative features among the various frequency domains. Moreover, to realize the nonlinear mapping capability of the network, the Relu activation function [52] is adopted to ensure that the outputs of the graph filtering layer are non-negative. Finally, the outputs of activation function are further sent to a multi-layer full connection network and a softmax function is also used to predict the desired class label information of the input EEG features.

具体地说，DGCNN模型的输入对应于从多个频段提取的EEG特征，例如五个频段(δ频段、θ频段、α频段、β频段和γ频段)，其中每个EEG通道被表示为DGCNN模型中的一个节点。遵循图过滤操作是一个 1×1 的卷积层，旨在学习各个频域之间的判别特征。此外，为了实现网络的非线性映射能力，采用Relu激活函数[52]来保证图滤波层的输出是非负的。最后，激活函数的输出进一步发送到多层全连接网络，并使用 softmax 函数来预测输入 EEG 特征的期望类标签信息。

B. Algorithm for DGCNN

To optimize the optimal network parameters, we adopt the back propagation (BP) method to iteratively update the network parameters until the optimal or suboptimal solutions are achieved. For this purpose, we define a loss function based on cross entropy cost, which is expressed as the following form:

为了优化最优网络参数，我们采用反向传播(BP)方法迭代更新网络参数，直到达到最优或次优解。为此，我们定义了一个基于交叉熵成本的损失函数，表示为以下形式：

where l and lp denote the actual label vector of training data and the predicted one, respectively, Θ denotes all the model parameters and α is the trade-off regularization weight. The cross entropy function cross entropy(l, lp) aims at measuring the dissimilarity between the actual emotional labels and the desired ones while the regularization α‖Θ‖ aims to prevent over-fitting of the model parameters learning.

其中 l 和 lp 分别表示训练数据和预测数据的实际标签向量，Θ 表示所有模型参数，α 是权衡正则化权重。交叉熵函数交叉熵 (l, lp) 旨在测量实际情感标签和所需情感标签之间的差异，而正则化 α‖Θ‖ 旨在防止模型参数学习的过度拟合。

When applying the BP method to dynamically learn the optimal adjacency matrix W∗ of the DGCNN model,we have to calculate the partial derivative of the loss function with respect to W∗, which is formulated as:

在应用BP方法动态学习DGCNN模型的最优邻接矩阵W *时，我们必须计算损失函数对W *的偏导数，公式为:

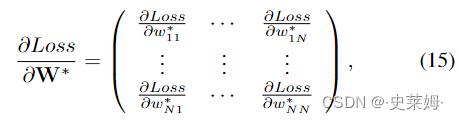
where w∗ij denotes the i-th row and j-column element of W∗. According to the chain rule, the calculation of ∂Loss ∂w∗ijcan be expressed as:

其中 w∗ij 表示 W∗ 的第 i 行和 j 列元素。根据链式法则，∂Loss∂w∗ij的计算可以表示为:

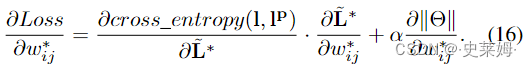
After calculating the partial derivative of ∂Loss ∂W∗ , we can use the following rule to update the optimal adjacency matrix W∗:

在计算∂Loss∂W∗的偏导数后，我们可以使用以下规则来更新最优邻接矩阵W∗：

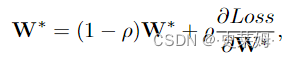
where ρ denotes the learning rate of the network. Algorithm 1 summarizes the detailed procedures of training the DGCNN model in EEG emotion recognition.

其中 ρ 表示网络的学习率设置为。算法 1 总结了 DGCNN 模型在 EEG 情感识别中训练的详细过程

IV. EXPERIMENTS

In this section, we will conduct extensive experiments on two emotional EEG databases that are commonly used in EEG emotion recognition to evaluate the effectiveness of the proposed GDCNN method. The first one is the SJTU Emotion EEG Database (SEED) [18] while the second one is the DREAMER [53].

在本节中，我们将对两个通常用于EEG情感识别的情感EEG数据库进行了广泛的实验，以评估所提出的GDCNN方法的有效性。第一个是SJTU情绪脑电图数据库(SEED)[18]，第二个是DREAMER[53]。

A. Emotional EEG Databases

The SEED database contains EEG data of 15 subjects (7 males and 8 females), which are collected via 62 EEG electrodes from the subjects when they are watching fifteen

中间没翻译好多

We investigate five kinds of features to evaluate the proposed EEG emotion recognition method, i.e., the differential entropy feature (DE), the power spectral density feature (PSD), the differential asymmetry feature (DASM), the rational asymmetry feature (RASM), and the differential caudality feature (DCAU). The features are respectively extracted in each of the frequency bands (δ band, θ band, α band, β band, andγ). Moreover, to extract the EEG feature, each trial of EEG signal flow is partitioned into a set of blocks, where each block contains 1s of EEG signals. In this case, we can extract five kinds of features from each block. The number of EEG features extracted from each frequency band corresponding to the various feature types are summarized in Table I.

我们研究了五种特征来评估所提出的EEG情绪识别方法，即差分熵特征(DE)、功率谱密度特征(PSD)、差分不对称特征(DASM)、理性不对称特征(RASM)和差分尾特征(DCAU)。这些特征分别在每个频段（δ 波段、θ 波段、α 波段、β 波段和 γ）中提取。此外，为了提取脑电特征，将脑电信号的每一次试验划分为一组块，每个块包含1秒的脑电信号。在这种情况下，我们可以从每个块中提取五种特征。表 I 总结了从对应于各种特征类型的每个频带中提取的 EEG 特征的数量。 

TABLE I

NUMBER OF THE FIVE TYPES OF EEG FEATURES EXTRACTED FROM EACH FREQUENCY BAND ON SEED DATABASE.

表 I

从种子数据库上的 EACH FREQUENCY BAND 提取的 EEG 特征类型的数量。

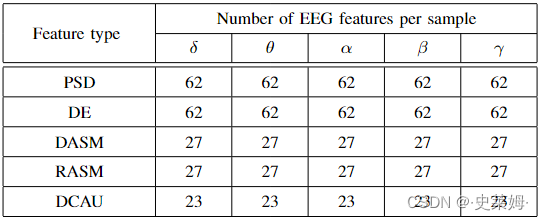
Based on the EEG features shown in Table I, we can train the DGCNN model shown in Fig.2 for the EEG emotion recognition. In this case, each vertex node of the graph in the DGCNN model is associated with five EEG features corresponding to the five frequency bands. It is notable that the number of vertex nodes in the graph would be different for different feature types since different feature types may contain different feature numbers. Specifically, for both PSD and DE features, the number vertex nodes in the graph is 62 whereas it would be 27 nodes for both DASM and RASM because there are only 27 features for these two feature types.

基于表I所示的EEG特征，我们可以训练图2所示的DGCNN模型进行EEG情感识别。在这种情况下，DGCNN模型中图的每个顶点节点与5个频段对应的5个EEG特征相关联。值得注意的是，对于不同的特征类型，图中顶点节点的数量会有所不同，因为不同的特征类型可能包含不同的特征数字。具体来说，对于 PSD 和 DE 特征，图中的节点数为 62，而对于 DASM 和 RASM，这将是 27 个节点，因为这两种特征类型只有 27 个特征。

TABLE II

COMPARISONS OF THE AVERAGE ACCURACIES AND STANDARD DEVIATIONS (%) OF SUBJECT DEPENDENT EEG-BASED EMOTION RECOGNITION EXPERIMENTS ON SEED DATABASE AMONG THE VARIOUS METHODS.

不同方法种子数据库基于脑电图的情绪识别实验的平均准确率和标准差(%)的比较。

Similarly, the number of vertex nodes in the graph would be 23 for DCAU feature type.

类似地，DCAU 特征类型的图中顶点节点数将为 23

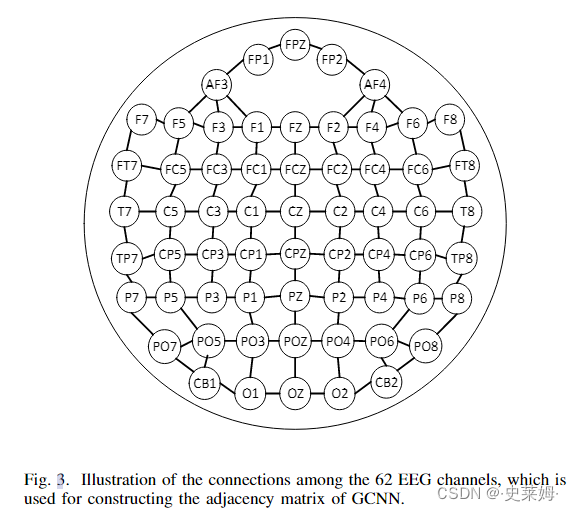
图3所示。62个脑电通道之间的连接说明，用于构建GCNN的邻接矩阵。

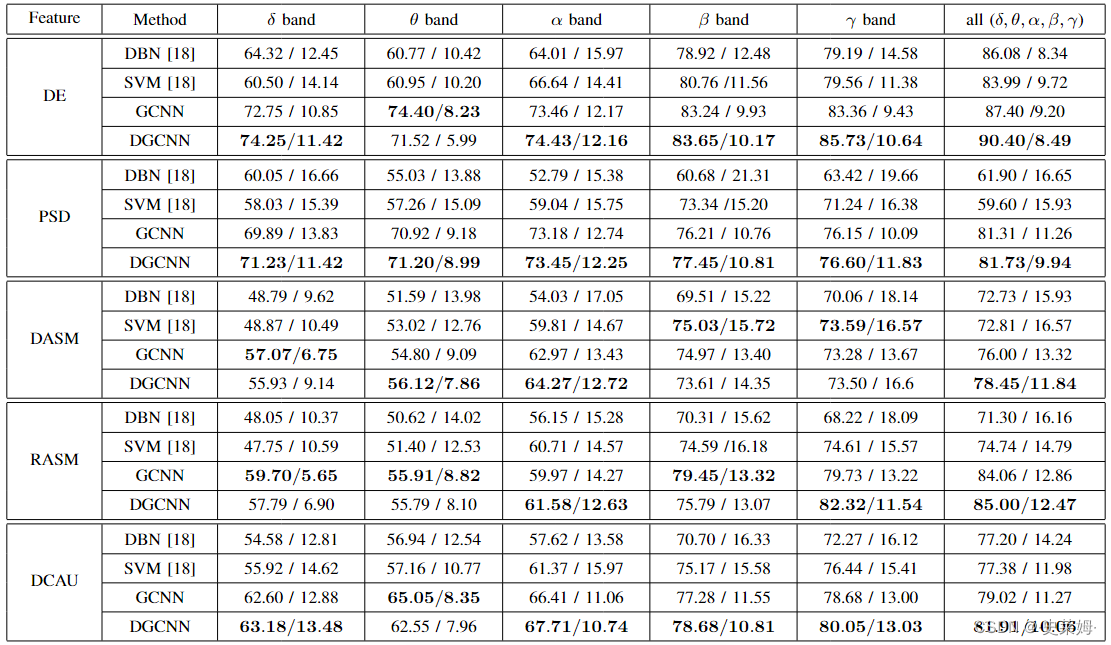
Table II summarizes experimental results in terms of the average EEG emotion recognition accuracies and the standard deviations of the DGCNN method under the five different EEG feature types (PSD, DE, DASM, RASM and DCAU features) and the five different frequency bands,where the notation of "all" means that the EEG features associated with all of the five frequency bands are combined such that each vertex node of the graph is associated with five EEG features. For the comparison purpose, we also include the experimental results of [18] with deep belief networks (DBN) [54] and support vector machine (SVM) [55] in Table II. Moreover, we also conduct the same experiments using the GCNN method to serve as a baseline method to evaluate the performance of DGCNN. Here it should be noted that, for the GCNN model, the elements of the adjacency matrix are predetermined according to the spatial relationship of the EEG channels. Fig.3 shows the spatial relationship, i.e., there is a direct connection or not between two EEG channels, of the 62 EEG channels. This relationship is used to construct the adjacency matrix for the GCNN model.
表 II 总结了 DGCNN 方法在五种不同的 EEG 特征类型（PSD、DE、DASM、RASM 和 DAU 特征）和五个不同频段下的平均 EEG 情绪识别准确度和标准偏差的实验结果，其中“all”的符号意味着与所有五个频段相关的 EEG 特征被组合，使得图的每个顶点节点与五个 EEG 特征相关联。为了比较的目的，我们还在表二中包含了[18]与深度信念网络(DBN)[54]和支持向量机(SVM)[55]的实验结果。此外，我们还使用GCNN方法进行了相同的实验，作为评价DGCNN性能的基准方法。这里需要注意的是，对于 GCNN 模型，邻接矩阵的元素是根据 EEG 通道之间的空间关系预先确定的。图 3 显示了 62 个 EEG 通道的两个 EEG 通道之间存在直接连接，即两个 EEG 通道之间没有直接连接。这种关系用于构建 GCNN 模型的邻接矩阵。

From Table II, we can observe the following major points:• Among the five kinds of EEG features, the DE feature was demonstrated to be better than most of the other ones in terms of the average recognition accuracy. For each emotion recognition method, the best average recognition accuracy was achieved when all the five frequency bands are used together. Especially, the best average recognition accuracy of DE feature was as high as 90.4% (with standard deviation of 8.49%) when all the five frequency bands were used.

从表 II 中，我们可以观察到以下要点： • 在五种 EEG 特征中，DE 特征在平均识别准确率方面优于大多数其他特征。对于每个情感识别方法，当所有五个频段一起使用时，获得了最好的平均识别精度。特别是，当使用所有五个频段时，DE 特征的最佳平均识别准确率高达 90.4%（标准偏差为 8.49%）。

Among the four EEG emotion recognition methods, both DGCNN and GCNN achieve better average recognition accuracies than the other two methods (SVM and DBN).

在四个EEG情感识别方法中，DGCNN和GCNN都比其他方法(SVM和DBN)获得了更好的平均识别精度。

TABLE III

THE AVERAGE ACCURACIES AND STANDARD DEVIATIONS (%) OF SUBJECT INDEPENDENT LOSO CROSS VALIDATION EEG-BASED EMOTION RECOGNITION EXPERIMENTS ON SEED DATABASE USING DGCNN.

表 III 使用 DGCNN 在种子数据库上使用 SEED 进行基于受试者损失的交叉验证 EEG 的情绪识别实验的平均准确度和标准偏差 (%)。

Compared with GCNN, however, DGCNN demonstrates to be more powerful in classifying the EEG emotion classes in most cases when the same EEG feature is used. This is most likely due to the optimization for determining the entries of the adjacency matrix in the GCNN model, which makes it more accurate to characterize the relationship between the various EEG channels.

然而，与 GCNN 相比，DGCNN 在大多数情况下在使用相同的 EEG 特征时被证明在对 EEG 情感类别进行分类方面更强大。这可能是由于优化确定GCNN模型中邻接矩阵的条目，这使得表征各种EEG通道之间的关系更加准确。

Among the five EEG frequency bands, both β and γfrequency bands achieve better recognition results than the other three ones in most cases. This indicates that the higher frequency bands may be more closely related with the emotion activities whereas the lower frequency bands are less related with the emotion activities.

在五个脑电频段中，β频段和γ频段在大多数情况下都比其他三个频段获得了更好的识别结果。这表明较高的频段可能与情绪活动更密切相关，而较低的频段与情绪活动的相关性较低。

2) Subject-independent Experiments on SEED: In the subject-independent experiments, we adopt the leave-onesubject-out (LOSO) cross-validation strategy to evaluate the EEG emotion recognition performance of the proposed DGCNN method. Specifically, in LOSO cross-validation experimental protocol, the EEG data of 14 subjects are used for training the model and the EEG data of the rest one subject is used as testing data. The experiments are repeated such that the EEG data of each subject are used once as the testing data. The average classification accuracies and standard deviations corresponding to the five kinds of EEG features are respectively calculated.

2)SEED与主题无关的实验:在主题无关的实验中，我们采用留一主题交叉验证策略来评估DGCNN方法的EEG情绪识别性能。具体来说，在LOSO交叉验证实验协议中，14名受试者的EEG数据用于训练模型，其余被试的EEG数据用作测试数据。重复实验，使每个受试者的脑电图数据用作测试数据。分别计算了五种脑电特征对应的平均分类精度和标准差。

Table III summarizes the experimental results in terms of the average EEG emotion recognition accuracies and the standard deviations of DGCNN under the different kinds of EEG features and the different frequency bands. From Table III, we obtain the following major points:

表 III 总结了 DGCNN 在不同类型的 EEG 特征和不同频段下的平均 EEG 情绪识别准确度和标准偏差的实验结果。从表 III 中，我们得到以下主要点：

For each kind of feature, the recognition accuracies associated with higher frequency bands are better than the ones of lower frequency bands.

对于每一种特征，与较高频段相关的识别精度都优于低频频段的识别精度。

For each kind of feature, the best recognition accuracy is obtained when combining the features extracted from the five frequency bands together for emotion recognition. Especially, when the five frequency bands are used and DE feature is adopted, the best recognition accuracy (= 79.95%) is achieved.

对于每一种特征，将五个频段提取的特征组合在一起进行情感识别时，获得了最佳识别精度。特别是，当使用五个频段和 DE 特征时，实现了最佳识别精度（= 79.95%）。

Considering that the subject-independent emotion recognition task can be seen as a cross-domain emotion recognition problem, we adopt several popular cross-domain recognition methods, including transfer component analysis (TCA) [56], KPCA [57], transductive SVM (T-SVM) [58] and transductive parameter transfer (TPT)。Since the use of the DE features combined with the five frequency bands (δ, θ, α, β, and γ) had been demonstrated to be the most effective features in the EEG emotion recognition, we adopt these features to compare the EEG emotion recognition performance among the five methods. Fig.4 summarizes the experimental results. From the results of Fig.4, we can see that the proposed DGCNN method achieves the highest recognition accuracy (= 79.95%) among the five methods. In addition, we can also see that the standard deviation ( = 9.02%) of the proposed DGCNN is much lower than that of TCA, KPCA, T-SVM, and TPT, which indicates that DGCNN is much more stable compared with the other four methods.

考虑到与主体无关的情绪识别任务可以看作是一个跨领域的情绪识别问题，我们采用了几种流行的跨领域识别方法，包括转移分量分析(TCA)[56]、KPCA[57]、转导支持向量机(T-SVM)[58]和转导参数转移(TPT)[59]作为基准方法。由于DE特征与5个频段(δ，θ，α，β和γ)结合使用已被证明是EEG情绪识别中最有效的特征，我们采用这些特征来比较五种方法中EEG情绪识别性能。图4总结了实验结果。从图4的结果可以看出，所提出的DGCNN方法在五种方法中获得了最高的识别精度(= 79.95%)。此外，我们还可以看到，所提出的DGCNN的标准差(=9.02%)远低于TCA、KPCA、T-SVM和TPT的标准差，这表明与其他四种方法相比，DGCNN更加稳定。

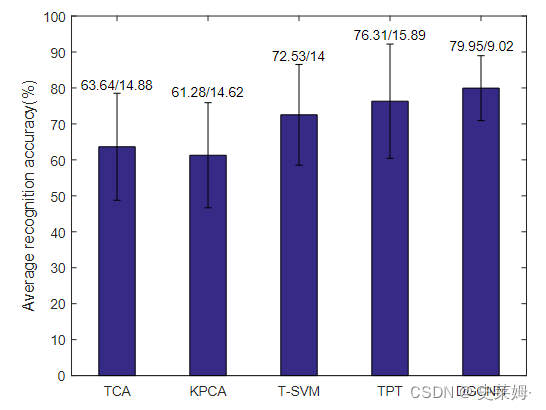
Fig. 4. Comparisons of the EEG emotion recognition accuracies and standard deviations among TCA, KPCA, T-SVM, TPT, and DGCNN.

图4所示。TCA、KPCA、T-SVM、TPT和DGCNN脑电图情绪识别精度和标准差的比较。

C. EEG Emotion Recognition Experiments on DREAMER Database

C.DREAMER数据库脑电图情绪识别实验

In this part, we conducted experiments on the DREAMER database to evaluate the EEG emotion recognition performance using the proposed DGCNN method. Before the experiments, we adopt the same feature extraction method as that of [53] to extract a set of PSD features. During the feature extraction, we firstly cropped the EEG signals corresponding to the last 60 seconds of each film clip and then decomposed the signals into θ (4-8Hz), α (8-13Hz), and β (13-20Hz) frequency bands.For each frequency band, the 60s EEG signals are further segmented into a set of 59 blocks by sliding a window with the size of 256 EEG points, in which there are half overlap between two subsequent blocks.  Finally, the PSD features were calculated from the EEG signal of each block.  As a result, we obtain 14 features associated with the 14 EEG channels in total from each block and we concatenate them into a 14-dimensional feature vector to represent a EEG data sample.  In this way, we totally obtain 59 EEG data samples associated with each frequency band from each session, which are used for our EEG emotion recognition evaluation of the DGCNN method.  Table IV shows the information about the EEG features we extracted from the DREAMER database.

在本节中，我们在 DREAMER 数据库上进行了实验，以使用所提出的 DGCNN 方法评估 EEG 情绪识别性能。在实验中，我们采用与[53]相同的特征提取方法来提取一组PSD特征。在特征提取过程中，我们首先裁剪每个电影片段最后60秒对应的脑电图信号，然后将信号分解为θ (4-8Hz)、α (8-13Hz)和β (13-20Hz)频段。对于每个频段，通过滑动一个256个脑电信号点大小的窗口，将60个脑电信号进一步分割为59个块，其中两个后续块之间有一半重叠。最后，对各块脑电信号进行PSD特征计算。因此，我们从每个块中获得了与14个脑电信号通道相关的14个特征，并将它们连接成一个14维特征向量来表示一个脑电信号数据样本。通过这种方法，我们从每个会话中获得59个与每个频带相关的脑电数据样本，用于DGCNN方法的脑电情绪识别评估。表4显示了我们从做梦者数据库中提取的脑电图特征信息。

TABLE IV

NUMBER OF THE PSD EEG FEATURES OF EACH EEG SAMPLE ASSOCIATED WITH EACH FREQUENCY BAND ON DREAMER DATABASE.

表 IV

与 DREAMER 数据库上的 EACH 频率BAND 相关的 EEG 样本的 PSD EEG 特征数。

To evaluate the EEG emotion recognition performance of the proposed DGCNN method, we adopt the subject-dependent leave-one-session-out cross-validation strategy to carry out the experiments. Specifically, for all the 18 sessions (corresponding to the 18 film clips) of experiments for each subject, we choose the EEG data samples belonging to one session as the testing data and use the ones belonging to the other 17 sessions as the training data. The emotion classification accuracy for the testing data samples is calculated based on the training data samples. This procedure is repeated for 18 trials such that the EEG data samples of each session have been used once as the testing data. Then, the overall classification accuracy of this subject is achieved by averaging the recognition accuracies of all the 18 trials. Finally, we use the average emotion classification accuracy obtained by averaging all the 23 subjects to evaluate the emotion recognition performance of the DGCNN method.

为了评估所提出的DGCNN方法的EEG情感识别性能，我们采用依赖于主题的留一会话交叉验证策略进行实验。具体来说，对于每个受试者的所有 18 个会话（对应于 18 个电影片段），我们选择属于一个会话的 EEG 数据样本作为测试数据，并使用属于其他 17 个会话的样本作为训练数据。测试数据样本的情感分类精度是根据训练数据样本计算的。重复此过程 18 次试验，以便每个会话的 EEG 数据样本已被用作测试数据。然后，通过对所有 18 次试验的识别精度进行平均，实现了该主题的整体分类精度。最后，我们使用平均所有 23 个主题获得的平均情感分类准确率来评估 DGCNN 方法的情感识别性能。

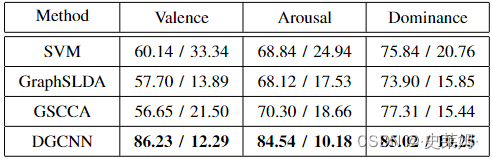
Table V shows the experimental results of the DGCNN method with respect to the emotion dimensions (i.e., valence, arousal, dominance). For comparison purpose, three state-ofthe-art methods, i.e., SVM, graph regularized sparse linear discriminant analysis (GraphSLDA) [60] and group sparse canonical correlation analysis (GSCCA) [8], are also used to conducted the same experiments and the experimental results are also included in Table V.

表 V 显示了 DGCNN 方法在情感维度（即效价、唤醒、支配）方面的实验结果。为了比较目的，还使用了三种最先进的方法，即 SVM、图正则化稀疏线性判别分析 (GraphSLDA) [60] 和组稀疏典型相关分析 (GSCCA) [8] 进行相同的实验，实验结果如表 V 所示。

TABLE V

THE AVERAGE CLASSIFICATION ACCURACIES AND STANDARD DEVIATIONS (%) OF SUBJECT-DEPENDENT EEG EMOTION RECOGNITION ON DREAMER DATABASE USING PSD FEATURE.

表 V

使用 PSD 特征在 DREAMER 数据库上主题依赖 EEG 情绪识别的平均分类准确度和标准偏差 (%)。

From Table V, we can obtain the following major points:

从表 V 中，我们可以得到以下主要点：

The proposed DGCNN method achieves much higher classification accuracies than the other three state-of-theart methods, in which the classification accuracies could be as high as 86.23% for valence classification, 84.54%for arousal classification, and 85.02% for dominance classification, respectively.

所提出的 DGCNN 方法比其他三种最先进的方法实现了更高的分类精度，其中效价分类的分类准确率可能高达 86.23%，唤醒分类的分类准确率高达 84.54%，优势分类的分类准确率分别为 85.02%。

The proposed DGCNN achieves more stable results than SVM, GraphSLDA, and GSCCA in terms of the standard deviations, in which the standard deviations are 12.29%for valence, 10.18% for arousal and 10.25% for dominance.

在标准偏差方面，所提出的 DGCNN 取得了比 SVM、GraphSLDA 和 GSCCA 更稳定的结果，其中效价的标准偏差为 12.29%，唤醒的标准偏差为 10.18%，优势为 10.25%。

V. CONCLUSIONS AND DISCUSSIONS

V.结论和讨论

In this paper, we have proposed a novel DGCNN model for EEG emotion recognition. Both subject dependent experiments and subject independent cross validation experiments on SEED EEG emotion database had been conducted and the experimental results indicated that the DGCNN method achieves better recognition performance than the state-of-the-art methods such as the SVM, DBN, KPCA, TCA, T-SVM and TPT methods. Especially, when the DE features of five frequency bands are combined together, the average recognition accuracy of DGCNN can be as high as 90.40% for the case of subject dependent experiments and can be as high as 79.95% for the case of subject independent cross validation experiments. On DREAMER dataset, the average accuracies of valence, arousal, and dominance using the proposed DGCNN are86.23%, 84.54% and 85.02% respectively, which are higher than SVM, GraphSLDA and GSCCA. The better recognition performance of DGCNN is most likely due to the following major points:

在本文中，我们提出了一种新的DGCNN脑电信号情感识别模型。对SEED EEG情感数据库进行了主题相关实验和主题独立交叉验证实验，实验结果表明，DGCNN方法比最先进的方法如SVM、DBN、KPCA、TCA、T-SVM和TPT方法具有更好的识别性能。特别是，当五个频段的DE特征组合在一起时，在主题相关实验的情况下，DGCNN的平均识别精度可达90.40%，在主题独立交叉验证实验的情况下，DGCNN的平均识别精度可达79.95%。在 DREAMER 数据集上，使用所提出的 DGCNN 的效价、唤醒和优势的平均准确率分别为 86.23%、84.54% 和 85.02%，高于 SVM、GraphSLDA 和 GSCCA。DGCNN 的更好识别性能很可能是由于以下主要点：

The use of nonlinear convolutional neural networks of DGCNN makes it much more powerful to deal with the nonlinear discriminative feature learning.

DGCNN的非线性卷积神经网络的使用使得处理非线性判别特征学习更加强大。

The graph representation of DGCNN provides a useful way to characterize the intrinsic relationships among the various EEG channels, which is advantageous for extracting the most discriminative features for the emotion recognition task.

DGCNN 的图形表示提供了一种有用的方法来表征各种 EEG 通道之间的内在关系，这有利于为情感识别任务提取最具辨别力的特征。

In contrast to GCNN, DGCNN adaptively learns the intrinsic relationships of EEG channels through optimization of the adjacency matrix W. However, the GCNN model determines the values of W prior to the model learning stage. Consequently, using the DGCNN method to characterize the relationships of EEG channels is more accurate than the GCNN method.

与 GCNN 相比，DGCNN 通过优化邻接矩阵 W 自适应地学习 EEG 通道的内在关系。然而，GCNN 模型在模型学习阶段之前确定 W 的值。因此，使用DGCNN方法来表征EEG通道之间的关系比GCNN方法更准确。

Additionally, it is notable that the diagonal elements of the adjacency matrix indicate the contributions of the EEG channels to the EEG emotion recognition. Hence, the adjacency matrix would provide a potential way to find out what are the most contributive EEG channels in the EEG emotion recognition, which would be advantageous to further improve the EEG emotion recognition performance. We leave this interesting topic as our future work.

此外，值得注意的是，邻接矩阵的对角元素表示EEG通道对EEG情绪识别的贡献。因此，邻接矩阵将为找出EEG情绪识别中贡献最大的EEG通道提供潜在的方法，这有利于进一步提高EEG情绪识别性能。我们将这个有趣的主题留作我们未来的工作。

Another interesting issue that should be investigated in future is about the data scale generalization. Although the proposed DGCNN method had demonstrated to be a good method in dealing with the EEG emotion recognition, it is also notable that the data scales of the EEG databases used in the experiments are still relatively small, which would not be enough for learning more powerful deep neural network models and hence may limit the further performance improvement in this research. Consequently, an EEG database with much larger scales is desired in solving this problem and this is also a major task of our future work.

另一个值得研究的问题是数据尺度的泛化。虽然提出的DGCNN方法在处理脑电情绪识别方面已经被证明是一种很好的方法，但值得注意的是，实验中使用的脑电数据库的数据规模仍然比较小，不足以学习更强大的深度神经网络模型，因此可能会限制本研究进一步的性能提升。因此，需要一个规模更大的脑电图数据库来解决这一问题，这也是我们未来工作的主要任务。