AllinToyou

这个屌丝很懒，什么也没留下！

热门标签

GWAS分析中SNP解释百分比PVE | 第二篇，GLM模型中如何计算PVE？

作者：AllinToyou | 2024-05-15 16:53:31

踩

gwas分析中snp解释百分比pve

上一篇，介绍了一下显著性的SNP，他们的解释表型变异百分比（PVE）之和，为何可能大于1.

https://yijiaobani.blog.csdn.net/article/details/122093602

这篇我们介绍一下GLM模型中，PVE的计算方法。

1. 数据描述

协变量是PCA的前三个，数据具体如下：

表型数据：

1641 1641 153.973423
1642 1642 113.119301
1643 1643 77.094801
1644 1644 89.293866
1645 1645 94.511433
1646 1646 134.410909
1647 1647 121.246759
1648 1648 45.699443
1649 1649 67.786229
1650 1650 102.225648

1
2
3
4
5
6
7
8
9
10
11

协变量数据

1641 1641 0.0633225 0.0285328 -0.00734127
1642 1642 0.0684039 0.0212648 -0.000664363
1643 1643 0.0609595 0.0242615 -0.00206211
1644 1644 0.0636631 0.0241012 -0.00275062
1645 1645 0.0741456 0.0293644 0.00068775
1646 1646 0.114417 0.0443451 -0.0408687
1647 1647 0.111599 0.0400401 -0.0320522
1648 1648 0.100862 0.0344925 -0.0386237
1649 1649 0.107986 0.028411 -0.0312307
1650 1650 0.108836 0.0377951 -0.0314308

1
2
3
4
5
6
7
8
9
10
11

基因型数据：


FID IID PAT MAT SEX PHENOTYPE M4_A M6_T M9_T M11_A M17_A M19_A M22_A M24_A M27_A M31_
1641 1641 0 0 0 -9 0 1 2 1 0 0 1 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 1
1642 1642 0 0 0 -9 1 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0
1643 1643 0 0 0 -9 1 0 1 1 0 0 1 1 1 1 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 1 1 1 1
1644 1644 0 0 0 -9 1 0 1 1 0 0 1 1 1 1 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 1 1 1 1
1645 1645 0 0 0 -9 0 1 2 1 0 0 1 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 1
1646 1646 0 0 0 -9 1 0 0 0 0 0 0 2 2 2 1 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 1 1 0 0
1647 1647 0 0 0 -9 0 1 1 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0
1648 1648 0 0 0 -9 1 0 0 0 0 0 0 1 1 2 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0
1649 1649 0 0 0 -9 0 1 1 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0
1650 1650 0 0 0 -9 1 0 0 0 0 0 0 1 1 2 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0
1651 1651 0 0 0 -9 1 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0
1652 1652 0 0 0 -9 0 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0
1653 1653 0 0 0 -9 1 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0
1654 1654 0 0 0 -9 0 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0
1655 1655 0 0 0 -9 2 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0
1656 1656 0 0 0 -9 2 0 0 0 1 1 2 2 2 2 2 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1657 1657 0 0 0 -9 2 0 0 0 1 1 2 2 2 2 2 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1658 1658 0 0 0 -9 2 0 0 0 1 1 2 2 2 2 2 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

2. GAPIT软件分析`GLM`模型

GAPIT软件安装，见：如何安装GAPIT软件：https://zhuanlan.zhihu.com/p/268327005

数据及代码下载，请关注公众号：育种数据分析之放飞自我，进入知识星球进行相关下载和学习

分析代码如下：


library(data.table)
raw = fread("plink.raw",header=T)
raw[1:10,1:10]

map = fread("recode.map",header=F)
head(map)

rr = raw[,!c(1,3:6)]
names(rr) = c("taxa",map$V2)

mm = map[,c(2,1,4)]
names(mm) = c("Name","Chromosome","Position")
head(mm)
rr[1:10,1:10]

fwrite(rr,"mdp_numeric.txt",sep="\t")
fwrite(mm,"mdp_SNP_information.txt",sep="\t")

#

# GWAS 分析
library(data.table)
source("http://zzlab.net/GAPIT/GAPIT.library.R")
source("http://zzlab.net/GAPIT/gapit_functions.txt")

myGd = fread("mdp_numeric.txt",header=T,data.table = F)
myGM = fread("mdp_SNP_information.txt",header = T,data.table=F)

myY = fread("dat_plink.txt",data.table = F)
head(myY)

covar = fread("cov_plink.txt",data.table = F)[,-1]
names(covar)[1] = "Taxa"
head(covar)

myGAPIT = GAPIT(Y = myY[,c(1,3)],GD = myGd, GM = myGM,
                # PCA.total=3,
                CV = covar,
                model="GLM")

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

注意：

这里使用的是plink格式的表型和PCA结果，使用的是plink.raw文件为基因型数据
将其转化为gapit软件需要的格式
定义基因型和位置信息，定义表型，定义协变量，定义模型为GLM
结果文件为：GAPIT.GLM.V3.GWAS.Results.csv

3. GLM模型结果文件

结果文件如下：
包括：

SNP名称
染色体
物理位置
P值 # 重点关注
maf
Rsquare.of.Model.without.SNP # 重点关注
Rsquare.of.Model.with.SNP # 重点关注

SNP,Chromosome,Position ,P.value,maf,nobs,Rsquare.of.Model.without.SNP,Rsquare.of.Model.with.SNP,FDR_Adjusted_P-values,effect
M57157,12,44,0.0000000265778189052299,0.375,1000,0.0178325320026741,0.0488405467802565,0.000799726570858368,7.5184135943861
M57155,12,44,0.000000149990719134015,0.3275,1000,0.0178325320026741,0.0454335956044116,0.00115674059672426,7.24232622801506
M57156,12,44,0.000000149990719134015,0.3275,1000,0.0178325320026741,0.0454335956044116,0.00115674059672426,7.24232622801506
M98663,20,73,0.00000015377076726145,0.222,1000,0.0178325320026741,0.0453847644903734,0.00115674059672426,-7.81213756957444
M73233,15,64,0.000000512284630336812,0.2255,1000,0.0178325320026741,0.0430299031398552,0.00290006393781271,-7.52596405927775
M8452,2,69,0.000000578277953701437,0.435,1000,0.0178325320026741,0.0427934752525868,0.00290006393781271,-6.51962588787404
M45998,10,20,0.000000768626039613293,0.411,1000,0.0178325320026741,0.0422387923854602,0.00307979999092427,-6.69120649416338
M82957,17,57,0.00000112940850557263,0.1685,1000,0.0178325320026741,0.0414897712489706,0.00307979999092427,8.48568078650835
M82958,17,57,0.00000112940850557263,0.1685,1000,0.0178325320026741,0.0414897712489706,0.00307979999092427,8.48568078650835

1
2
3
4
5
6
7
8
9
10
11

这里，

P值为SNP的P值，我们根据它判断显著性，并根据它进行QQ图和曼哈顿图的绘制
Rsquare.of.Model.without.SNP # 这个是单位点不包括次SNP的解释百分比（R方）
Rsquare.of.Model.with.SNP # 这个是单位点包括此SNP的解释百分比（R方）

上面两者之差，即为该SNP的解释百分比（PVE）

$$SNP的PVE = Rsquare.of.Model.with.SNP - Rsquare.of.Model.without.SNP$$
1

4. 我们将结果读入R语言计算

首先读入R语言：

r$> re = fread("GAPIT.GLM.V3.GWAS.Results.csv")

r$> head(re)
      SNP Chromosome Position      P.value    maf nobs Rsquare.of.Model.without.SNP Rsquare.of.Model.with.SNP FDR_Adjusted_P-values    effect
1: M57157         12       44 2.657782e-08 0.3750 1000                   0.01783253                0.04884055          0.0007997266  7.518414
2: M57155         12       44 1.499907e-07 0.3275 1000                   0.01783253                0.04543360          0.0011567406  7.242326
3: M57156         12       44 1.499907e-07 0.3275 1000                   0.01783253                0.04543360          0.0011567406  7.242326
4: M98663         20       73 1.537708e-07 0.2220 1000                   0.01783253                0.04538476          0.0011567406 -7.812138
5: M73233         15       64 5.122846e-07 0.2255 1000                   0.01783253                0.04302990          0.0029000639 -7.525964
6:  M8452          2       69 5.782780e-07 0.4350 1000                   0.01783253                0.04279348          0.0029000639 -6.519626

1
2
3
4
5
6
7
8
9
10
11

然后我们根据上面的公式，手动计算PVE值：

r$> re$PVE = re$Rsquare.of.Model.with.SNP - re$Rsquare.of.Model.without.SNP

r$> head(re)
      SNP Chromosome Position      P.value    maf nobs Rsquare.of.Model.without.SNP Rsquare.of.Model.with.SNP FDR_Adjusted_P-values    effect        PVE
1: M57157         12       44 2.657782e-08 0.3750 1000                   0.01783253                0.04884055          0.0007997266  7.518414 0.03100801
2: M57155         12       44 1.499907e-07 0.3275 1000                   0.01783253                0.04543360          0.0011567406  7.242326 0.02760106
3: M57156         12       44 1.499907e-07 0.3275 1000                   0.01783253                0.04543360          0.0011567406  7.242326 0.02760106
4: M98663         20       73 1.537708e-07 0.2220 1000                   0.01783253                0.04538476          0.0011567406 -7.812138 0.02755223
5: M73233         15       64 5.122846e-07 0.2255 1000                   0.01783253                0.04302990          0.0029000639 -7.525964 0.02519737
6:  M8452          2       69 5.782780e-07 0.4350 1000                   0.01783253                0.04279348          0.0029000639 -6.519626 0.02496094

1
2
3
4
5
6
7
8
9
10
11

根据PVE的大小，进行排序，降序：

r$> re %>% arrange(-PVE)
          SNP Chromosome Position      P.value    maf nobs Rsquare.of.Model.without.SNP Rsquare.of.Model.with.SNP FDR_Adjusted_P-values        effect          PVE
    1: M57157         12       44 2.657782e-08 0.3750 1000                   0.01783253                0.04884055          0.0007997266  7.5184135944 3.100801e-02
    2: M57155         12       44 1.499907e-07 0.3275 1000                   0.01783253                0.04543360          0.0011567406  7.2423262280 2.760106e-02
    3: M57156         12       44 1.499907e-07 0.3275 1000                   0.01783253                0.04543360          0.0011567406  7.2423262280 2.760106e-02
    4: M98663         20       73 1.537708e-07 0.2220 1000                   0.01783253                0.04538476          0.0011567406 -7.8121375696 2.755223e-02
    5: M73233         15       64 5.122846e-07 0.2255 1000                   0.01783253                0.04302990          0.0029000639 -7.5259640593 2.519737e-02
   ---
30086: M58296         12       66 9.996606e-01 0.2700 1000                   0.01783253                0.01783253          0.9997934933  0.0006040638 1.785355e-10
30087:   M751          1       15 9.998043e-01 0.2435 1000                   0.01783253                0.01783253          0.9998960441  0.0003736382 5.935820e-11
30088: M21736          5       35 9.998296e-01 0.3020 1000                   0.01783253                0.01783253          0.9998960441  0.0002955665 4.500680e-11
30089: M80677         17       12 9.999131e-01 0.3830 1000                   0.01783253                0.01783253          0.9999300138 -0.0001448323 1.170910e-11
30090: M57593         12       52 9.999300e-01 0.2735 1000                   0.01783253                0.01783253          0.9999300138 -0.0001300807 7.589301e-12

1
2
3
4
5
6
7
8
9
10
11
12
13
14

可以看到，结果就给出了PVE从大到小的排序结果。

这里，我们注意到，前三个SNP的PVE分别是：

3.1%
2.76%
2.76%
而且，这三个SNP都在12号染色体的44个位置，因为这三个位点离得很近，都达到显著水平，PVE也很大，那我们可以认为附件有一个基因，显著影响表型。

这里，我们对PVE进行求和：

r$> sum(re$PVE)
[1] 57.6114

1
2
3

可以看到，总的PVE之和为57.611，远远大于1，是因为有些位点高度LD，所以PVE之和就很大。相关问题在 GWAS分析中SNP解释百分比PVE | 第一篇，SNP解释百分比之和为何大于1？中有过介绍。

5. 用R语言如何计算？

简单来说，就是单位点的回归分析，计算R方。

这里，我们用同样的数据，在R中进行GLM的GWAS分析。

代码如下：


library(data.table)
geno = fread("plink.raw")[,!c(1,3:6)]
map = fread("recode.map")
m012 = geno
names(m012) = c("IID",map$V2)
phe = fread("phe.txt")
cov1= fread("tcov.txt")

dat = left_join(phe,cov1,by = c("V1"="V1")) %>% dplyr::select(IID =1, y =2, pc1=3,pc2=4,pc3=5)
dat1 = left_join(dat,m012,by="IID")
# dat1$M57157 = as.factor(dat1$M57157)
mod_1 = lm(y ~  1+pc1 + pc2 + pc3 + M57157,data=dat1);summary(mod_1)
summary(mod_1)$r.squared

mod_2 = lm(y ~  1+pc1 + pc2 + pc3 ,data=dat1);summary(mod_2)
summary(mod_2)$r.squared
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

这里，我们将PCA的前三个作为协变量加到回归分析汇总。

包含SNP的回归分析：

r$> mod_1 = lm(y ~  1+pc1 + pc2 + pc3 + M57157,data=dat1);summary(mod_1)

Call:
lm(formula = y ~ 1 + pc1 + pc2 + pc3 + M57157, data = dat1)

Residuals:
    Min      1Q  Median      3Q     Max
-85.094 -19.174  -0.443  18.218  79.181

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept)   96.408      1.320  73.048  < 2e-16 ***
pc1         -108.543     27.603  -3.932 9.00e-05 ***
pc2           28.740     28.981   0.992   0.3216
pc3           58.098     27.890   2.083   0.0375 *
M57157         7.518      1.320   5.695 1.62e-08 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 27.6 on 995 degrees of freedom
Multiple R-squared:  0.04884,	Adjusted R-squared:  0.04502
F-statistic: 12.77 on 4 and 995 DF,  p-value: 3.838e-10

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

可以看到，R方为0.04884，也可以这样提取：

r$> summary(mod_1)$r.squared
[1] 0.04884055

1
2
3

不包含SNP的回归分析：

r$> mod_2 = lm(y ~  1+pc1 + pc2 + pc3 ,data=dat1);summary(mod_2)

Call:
lm(formula = y ~ 1 + pc1 + pc2 + pc3, data = dat1)

Residuals:
    Min      1Q  Median      3Q     Max
-89.495 -19.318  -0.099  18.649  85.448

Coefficients:
             Estimate Std. Error t value Pr(>|t|)
(Intercept)  102.0467     0.8864 115.129  < 2e-16 ***
pc1         -111.8205    28.0295  -3.989 7.11e-05 ***
pc2          -21.6604    28.0295  -0.773     0.44
pc3           35.1350    28.0295   1.254     0.21
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 28.03 on 996 degrees of freedom
Multiple R-squared:  0.01783,	Adjusted R-squared:  0.01487
F-statistic: 6.028 on 3 and 996 DF,  p-value: 0.0004546

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

这里的R方为：0.01783

也可以这样提取：

r$> x2 = summary(mod_2)$r.squared
    summary(mod_2)$r.squared
[1] 0.01783253

1
2
3
4

那么SNP：M57157的PVE为：3.1%

r$> x1 - x2
[1] 0.03100801

1
2
3

对比我们GAPIT的PVE结果：

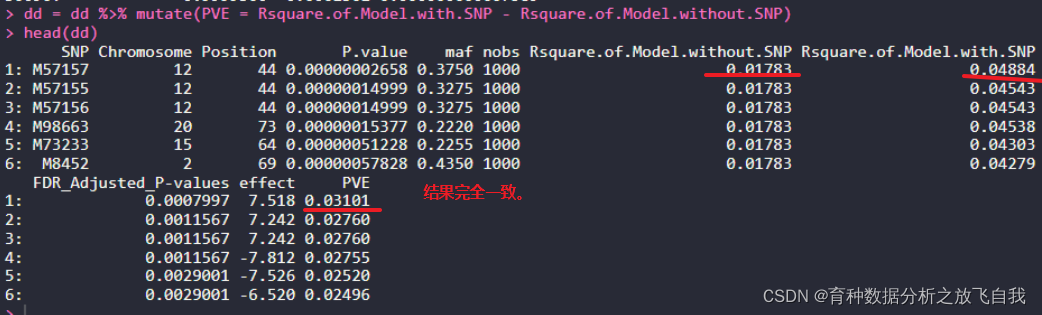
结果完全一致。

这里，一般线性模型中，可以针对显著性的SNP，进行单位点回归分析，计算PVE。对于混合线性模型，也可以将显著性位点提取，进行R语言的手动计算，这个也是PVE计算的一种方法。

混合线性模型中，还有其它的计算方法，我们后面进行介绍，欢迎继续关注我。

6. 数据和代码下载方法