强化学习------DDPG算法(附pytorch代码)

一、前言

Deep Deterministic Policy Gradient (DDPG)算法是DeepMind团队提出的一种专门用于解决连续控制问题的在线式(on-line)深度强化学习算法，它其实本质上借鉴了Deep Q-Network (DQN)算法里面的一些思想。论文和源代码如下：
论文：https://arxiv.org/pdf/1509.02971.pdf

代码：https://github.com/indigoLovee/DDPG

本文将会介绍其基本原理，并实现DDPG算法来训练游戏的例子

二、基本原理

DDPG（Deep Deterministic Policy Gradient）是一种用于解决连续动作空间问题的深度强化学习算法，结合了确定性策略和经验回放的思想。下面是DDPG算法的主要特点和步骤：

1. Actor-Critic架构：DDPG算法基于Actor-Critic框架，其中Actor负责学习确定性策略，即在给定状态下直接输出动作值；Critic负责学习值函数，评估当前状态的价值。

2. 确定性策略：与传统的策略梯度方法不同，DDPG使用确定性策略，即直接输出动作值而不是动作的概率分布。这有助于在连续动作空间中更好地学习策略。

3. 经验回放：为了解决样本相关性和稳定性问题，DDPG引入了经验回放机制，将Agent与环境交互得到的经验存储在经验回放缓冲区中，然后从中随机采样进行训练。

4. 目标网络：为了稳定训练，DDPG使用目标网络来估计目标Q值和目标策略。目标网络的参数是通过软更新的方式从主网络的参数逐渐更新得到的。

5. 噪声探索：确定性策略输出的动作为确定性动作，缺乏对环境的探索。在训练阶段，给Actor网络输出的动作加入噪声，从而让智能体具备一定的探索能力。

为什么引入目标网络？

在深度强化学习中，引入目标网络是为了解决训练过程中的不稳定性和提高算法的收敛性。具体来说，引入目标网络主要有以下两个作用：

稳定训练：在训练深度强化学习模型时，目标网络的引入可以减少训练过程中的“moving target”问题。在训练Q网络或者Actor网络时，如果每次更新都直接影响到当前的网络参数，会导致目标值的变化，从而使得训练不稳定。通过引入目标网络，可以固定目标网络的参数一段时间，使得目标值更加稳定，有利于训练的收敛。

减少估计误差：在深度强化学习中，通常会使用TD目标来更新Q值或者Actor策略。而直接使用当前的网络来估计TD目标可能会引入较大的估计误差，导致训练不稳定。通过引入目标网络，可以使用目标网络来估计TD目标，减少估计误差，从而提高算法的稳定性和收敛性。

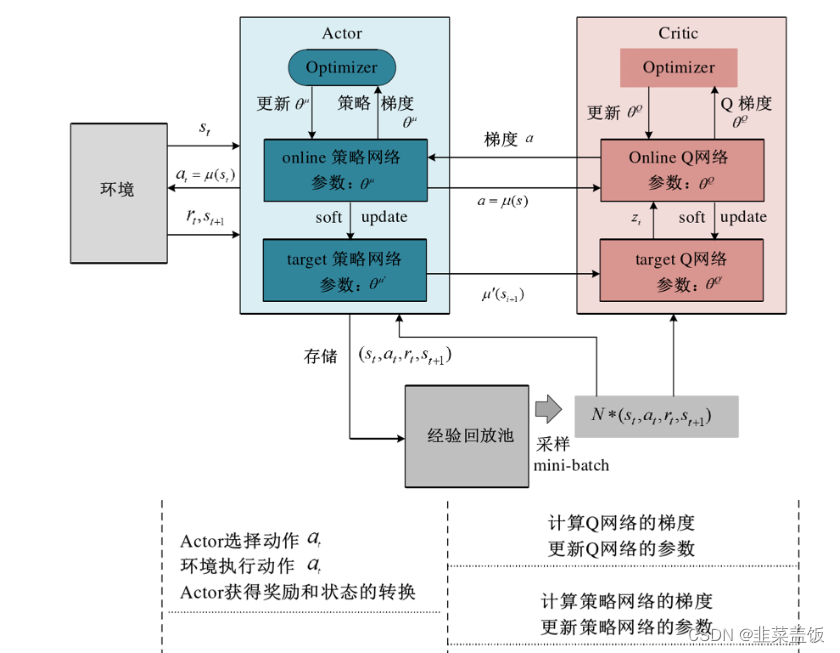
DDPG 算法的原理如下图所示：

2.1、经验回放

经验回放就是一种让经验概率分布变得稳定的技术，可以提高训练的稳定性。经验回放主要有“存储”和“回放”两大关键步骤：

存储：将经验以$(s_t,a_t,r_{t+1},s_{t+1},done)$形式存储在经验池中。

回放：按照某种规则从经验池中采样一条或多条经验数据。

本质上就是与DQN算法一样的经验回放操作

2.2、更新过程

DDPG 共包含 4 个神经网络，用于对 Q 值函数和策略的近似表示。

由于DDPG算法是基于AC框架，因此算法中必然含有Actor和Critic网络。另外每个网络都有其对应的目标网络，所以DDPG算法中包括四个网络，分别是Actor网络$\mu (\cdot |{\theta }^{\mu })$，Critic网络$Q(\cdot |{\theta }^Q)$，Target Actor网络${\mu }^{{}^{\prime }}(\cdot |{\theta }^{u^{\prime }})$和Target Critic网络$Q^{{}^{\prime }}(\cdot |{\theta }^{Q^{\prime }})$ 。

算法更新主要更新的是Actor和Critic网络的参数，其中Actor网络通过最大化累积期望回报来更新，Critic网络通过最小化评估值与目标值之间的误差来更新。在训练阶段，我们从Replay Buffer中采样一个批次的数据，假设采样到的一条数据为，Actor和Critic网络更新过程如下。

2.2.1、Critic网络更新过程

1、利用Target Actor网络计算出状态$s^{{}^{\prime }}$(下一个状态)下的动作：

$a^{{}^{\prime }}$ = ${\mu }^{{}^{\prime }}(s^{{}^{\prime }}|{\theta }^{u^{\prime }})$

2、然后利用Target Critic网络计算出状态动作对(s,a)的目标值：

$y=r+\gamma (1-done)Q^{{}^{\prime }}(s^{{}^{\prime }},a^{{}^{\prime }}|{\theta }^{Q^{\prime }})$

3、接着利用 Critic网络计算出状态动作对(s,a)的评估值：

$a=Q(s,a|{\theta }^Q)$

4、最后利用梯度下降算法最小化评估值和期望值之间的差值$L_c$，从而对Critic网络中的参数进行更新：

$L_c=(y-q{)}^2$

更新过程本质上跟DQN算法的更新过程很类似

2.2.2、Actor网络更新过程

1、利用Actor网络计算出状态s下的动作：

$q_{new}=\mu (s|{\theta }^{\mu })$

2、然后利用Critic网络计算出状态动作对$(s,a_{new})$的评估值**（即累积期望回报）**：

$q_{new}=Q(s,a_{new}|{\theta }^Q)$

3、最后利用梯度上升算法最大化累积期望回报$q_{new}$

注意：代码实现是采用梯度下降算法优化$-q_{new}$，其实本质上都是一样的，从而对Actor网络中的参数进行更新。

至此我们就完成了对Actor和Critic网络的更新。

2.2.3、 目标网络的更新

目标网络更新要简单得多，我们通过软更新的方式来更新目标更新
即引入一个学习率（或者成为动量）$\tau$，将旧的目标网络参数和新的对应网络参数做加权平均，然后赋值给目标网络，学习率（动量）$\tau \in (0,1)$，通常取值0.005。
Target Actor网络更新过程：

${\theta }^{{\mu }^{{}^{\prime }}}=\tau {\theta }^{\mu }+(1-\tau ){\theta }^{{\mu }^{{}^{\prime }}}$

Target Critic网络更新过程：

${\theta }^{Q^{{}^{\prime }}}=\tau {\theta }^Q+(1-\tau ){\theta }^{Q^{{}^{\prime }}}$

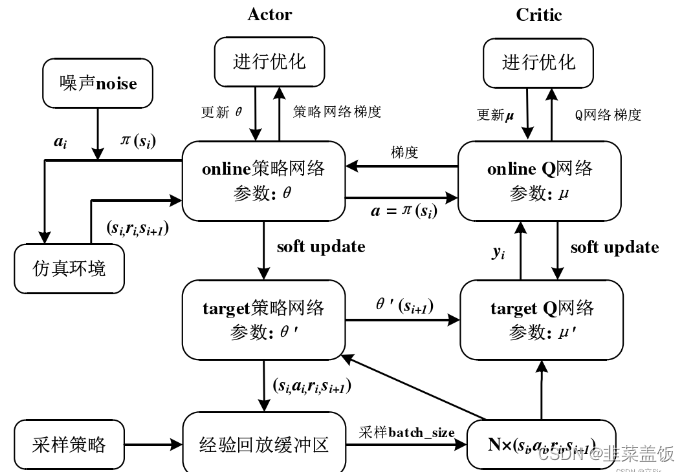
至此我们的四个网络全部更新完毕，整体的更新流程图如下：

2.3、噪音探索

在DDPG算法中，为了在学习过程中引入一定的探索性，通常会使用噪音来探索动作空间。噪音的引入可以帮助Agent在训练过程中探索不同的动作选择，从而更好地发现最优策略。

在代码中我们采取行为时使用高斯噪音的探索方法

 action = action + self.sigma * np.random.randn(self.n_actions)
1

在这个公式中np.random.randn(self.n_actions)生成了一个服从标准正态分布的随机向量，乘以self.sigma后被添加到当前的action中。这种方式属于对动作空间添加高斯噪音的探索方法。

self.sigma是用来控制噪音的强度的参数，通过调节self.sigma的大小可以控制噪音的方差。将高斯噪音添加到动作中可以使Agent在探索过程中具有一定的随机性，从而更好地探索动作空间，发现可能的最优策略。

三、算法代码实现

伪代码如下：

算法代码如下：

import torch
from torch import nn
from torch.nn import functional as F
import numpy as np
import collections
import random
 
# ------------------------------------- #
# 经验回放池
# ------------------------------------- #
 
class ReplayBuffer:
    def __init__(self, capacity):  # 经验池的最大容量
        # 创建一个队列，先进先出
        self.buffer = collections.deque(maxlen=capacity)
    # 在队列中添加数据
    def add(self, state, action, reward, next_state, done):
        # 以list类型保存
        self.buffer.append((state, action, reward, next_state, done))
    # 在队列中随机取样batch_size组数据
    def sample(self, batch_size):
        transitions = random.sample(self.buffer, batch_size)
        # 将数据集拆分开来
        state, action, reward, next_state, done = zip(*transitions)
        return np.array(state), action, reward, np.array(next_state), done
    # 测量当前时刻的队列长度
    def size(self):
        return len(self.buffer)
 
# ------------------------------------- #
# 策略网络
# ------------------------------------- #
 
class PolicyNet(nn.Module):
    def __init__(self, n_states, n_hiddens, n_actions, action_bound):
        super(PolicyNet, self).__init__()
        # 环境可以接受的动作最大值
        self.action_bound = action_bound
        # 只包含一个隐含层
        self.fc1 = nn.Linear(n_states, n_hiddens)
        self.fc2 = nn.Linear(n_hiddens, n_actions)
    # 前向传播
    def forward(self, x):
        x = self.fc1(x)  # [b,n_states]-->[b,n_hiddens]
        x = F.relu(x)
        x = self.fc2(x)  # [b,n_hiddens]-->[b,n_actions]
        x= torch.tanh(x)  # 将数值调整到 [-1,1]
        x = x * self.action_bound  # 缩放到 [-action_bound, action_bound]
        return x
 
# ------------------------------------- #
# 价值网络
# ------------------------------------- #
 
class QValueNet(nn.Module):
    def __init__(self, n_states, n_hiddens, n_actions):
        super(QValueNet, self).__init__()
        # 
        self.fc1 = nn.Linear(n_states + n_actions, n_hiddens)
        self.fc2 = nn.Linear(n_hiddens, n_hiddens)
        self.fc3 = nn.Linear(n_hiddens, 1)
    # 前向传播
    def forward(self, x, a):
        # 拼接状态和动作
        cat = torch.cat([x, a], dim=1)  # [b, n_states + n_actions]
        x = self.fc1(cat)  # -->[b, n_hiddens]
        x = F.relu(x)
        x = self.fc2(x)  # -->[b, n_hiddens]
        x = F.relu(x)
        x = self.fc3(x)  # -->[b, 1]
        return x
 
# ------------------------------------- #
# 算法主体
# ------------------------------------- #
 
class DDPG:
    def __init__(self, n_states, n_hiddens, n_actions, action_bound,
                 sigma, actor_lr, critic_lr, tau, gamma, device):
 
        # 策略网络--训练
        self.actor = PolicyNet(n_states, n_hiddens, n_actions, action_bound).to(device)
        # 价值网络--训练
        self.critic = QValueNet(n_states, n_hiddens, n_actions).to(device)
        # 策略网络--目标
        self.target_actor = PolicyNet(n_states, n_hiddens, n_actions, action_bound).to(device)
        # 价值网络--目标
        self.target_critic = QValueNet(n_states, n_hiddens, n_actions).to(device
                                                                          )
        # 初始化价值网络的参数，两个价值网络的参数相同
        self.target_critic.load_state_dict(self.critic.state_dict())
        # 初始化策略网络的参数，两个策略网络的参数相同
        self.target_actor.load_state_dict(self.actor.state_dict())
 
        # 策略网络的优化器
        self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
        # 价值网络的优化器
        self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)
 
        # 属性分配
        self.gamma = gamma  # 折扣因子
        self.sigma = sigma  # 高斯噪声的标准差，均值设为0
        self.tau = tau  # 目标网络的软更新参数
        self.n_actions = n_actions
        self.device = device
 
    # 动作选择
    def take_action(self, state):
        # 维度变换 list[n_states]-->tensor[1,n_states]-->gpu
        state = torch.tensor(state, dtype=torch.float).view(1,-1).to(self.device)
        # 策略网络计算出当前状态下的动作价值 [1,n_states]-->[1,1]-->int
        action = self.actor(state).item()
        # 给动作添加噪声，增加搜索
        action = action + self.sigma * np.random.randn(self.n_actions)
        return action
    
    # 软更新, 意思是每次learn的时候更新部分参数
    def soft_update(self, net, target_net):
        # 获取训练网络和目标网络需要更新的参数
        for param_target, param in zip(target_net.parameters(), net.parameters()):
            # 训练网络的参数更新要综合考虑目标网络和训练网络
            param_target.data.copy_(param_target.data*(1-self.tau) + param.data*self.tau)
 
    # 训练
    def update(self, transition_dict):
        # 从训练集中取出数据
        states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)  # [b,n_states]
        actions = torch.tensor(transition_dict['actions'], dtype=torch.float).view(-1,1).to(self.device)  # [b,1]
        rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1,1).to(self.device)  # [b,1]
        next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)  # [b,next_states]
        dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1,1).to(self.device)  # [b,1]
        
        # 价值目标网络获取下一时刻的动作[b,n_states]-->[b,n_actors]
        next_q_values = self.target_actor(next_states)
        # 策略目标网络获取下一时刻状态选出的动作价值 [b,n_states+n_actions]-->[b,1]
        next_q_values = self.target_critic(next_states, next_q_values)
        # 当前时刻的动作价值的目标值 [b,1]
        q_targets = rewards + self.gamma * next_q_values * (1-dones)
        
        # 当前时刻动作价值的预测值 [b,n_states+n_actions]-->[b,1]
        q_values = self.critic(states, actions)
 
        # 预测值和目标值之间的均方差损失
        critic_loss = torch.mean(F.mse_loss(q_values, q_targets))
        # 价值网络梯度
        self.critic_optimizer.zero_grad()
        critic_loss.backward()
        self.critic_optimizer.step()
 
        # 当前状态的每个动作的价值 [b, n_actions]
        actor_q_values = self.actor(states)
        # 当前状态选出的动作价值 [b,1]
        score = self.critic(states, actor_q_values)
        # 计算损失
        actor_loss = -torch.mean(score)
        # 策略网络梯度
        self.actor_optimizer.zero_grad()
        actor_loss.backward()
        self.actor_optimizer.step()
 
        # 软更新策略网络的参数  
        self.soft_update(self.actor, self.target_actor)
        # 软更新价值网络的参数
        self.soft_update(self.critic, self.target_critic)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164

四、训练示例

基于 OpenAI 的 gym 环境完成一个推车游戏，目标是将小车推到山顶旗子处。动作维度为1，属于连续值；状态维度为 2，分别是 x 坐标和小车速度。
代码结构如下：

训练代码如下：

import numpy as np
import torch
import matplotlib.pyplot as plt
import gym
# from parsers import args
from ddpg import ReplayBuffer, DDPG

device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')

# -------------------------------------- #
# 环境加载
# -------------------------------------- #

env_name = "MountainCarContinuous-v0"  # 连续型动作
env = gym.make(env_name)
n_states = env.observation_space.shape[0]  # 状态数 2
n_actions = env.action_space.shape[0]  # 动作数 1
action_bound = env.action_space.high[0]  # 动作的最大值 1.0

# -------------------------------------- #
# 模型构建
# -------------------------------------- #

# 经验回放池实例化
replay_buffer = ReplayBuffer(capacity=5000)
# 模型实例化
agent = DDPG(n_states=n_states,  # 状态数
             n_hiddens=100,  # 隐含层数
             n_actions=n_actions,  # 动作数
             action_bound=action_bound,  # 动作最大值
             sigma=0.05,  # 高斯噪声
             actor_lr=0.001,  # 策略网络学习率
             critic_lr=0.001,  # 价值网络学习率
             tau=0.001,  # 软更新系数
             gamma=0.99,  # 折扣因子
             device=device
             )

# -------------------------------------- #
# 模型训练
# -------------------------------------- #

return_list = []  # 记录每个回合的return
mean_return_list = []  # 记录每个回合的return均值

for i in range(100):  # 迭代10回合
    episode_return = 0  # 累计每条链上的reward
    state = env.reset()  # 初始时的状态
    env.render()   #显示游戏
    done = False  # 回合结束标记

    while not done:
        # 获取当前状态对应的动作
        action = agent.take_action(state)
        # 环境更新
        next_state, reward, done, _ = env.step(action)
        # 更新经验回放池
        replay_buffer.add(state, action, reward, next_state, done)
        # 状态更新
        state = next_state
        # 累计每一步的reward
        episode_return += reward

        # 如果经验池超过容量，开始训练
        if replay_buffer.size() > 3:
            # 经验池随机采样batch_size组
            s, a, r, ns, d = replay_buffer.sample(2)
            # 构造数据集
            transition_dict = {
                'states': s,
                'actions': a,
                'rewards': r,
                'next_states': ns,
                'dones': d,
            }
            # 模型训练
            agent.update(transition_dict)

    # 保存每一个回合的回报
    return_list.append(episode_return)
    mean_return_list.append(np.mean(return_list[-10:]))  # 平滑

    # 打印回合信息
    print(f'iter:{i}, return:{episode_return}, mean_return:{np.mean(return_list[-10:])}')

# 关闭动画窗格
env.close()

# -------------------------------------- #
# 绘图
# -------------------------------------- #

x_range = list(range(len(return_list)))

plt.subplot(121)
plt.plot(x_range, return_list)  # 每个回合return
plt.xlabel('episode')
plt.ylabel('return')
plt.subplot(122)
plt.plot(x_range, mean_return_list)  # 每回合return均值
plt.xlabel('episode')
plt.ylabel('mean_return')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102

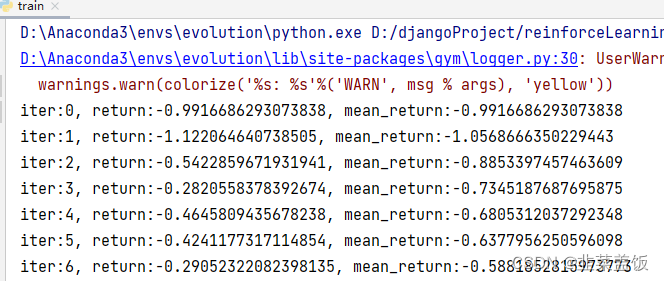
4.1、实现效果