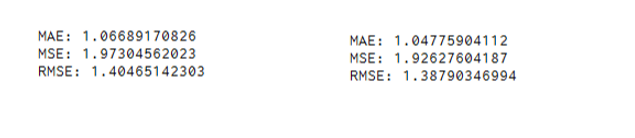10python数据分析-回归分析_python的多项回归算法有哪些类型
赞
踩
Python数据分析——第10周
回归分析
回归分析:通过建立模型来研究变量之间相互关系的密切程度、结构状态及进行模型预测的一种有效工具

一元线性回归:
多元线性回归:
多个因变量与多个自变量的回归:
一元非线性回归:对自变量或者因变量进行非线性的转换
分段回归:
多元非线性回归:
含有定性变量的回归:少年组、青年组、老年组,分别是0,、1、2
函数关系与相关关系
函数关系:确定性关系,y=3+10*x
自变量确定以后,因变量也能确定下来

相关关系:非确定性关系
即使你知道了自变量的值,但是你不能准确地预测出因变量的值,可能只能预测出因变量大概的范围或者均值。
相关系数
我们使用相关系数去衡量线性相关性的强弱。

每个自变量减去均值乘每个因变量减去均值,累加起来。除以。自变量的标准差乘上因变量的标准差。
强弱:这些点距离直线的距离。这些点越能接近于某条直线,那么它的线性关系越强。
正相关:x越大、y越大
负相关:x越大、y越小
通过计算,左图中的相关系数为0.9930858,右图的相关系数为0.9573288

一元线性回归模型
若X与Y之间存在着较强的相关关系,则我们有Y≈α+βX
若α与β的值已知,则给出相应的X值,我们可以根据Y≈α+βX得到相应的Y的预测值

误差:
把a和b求出来
参数
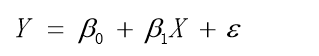
截距项α
斜率β
误差项ε
例子:商品销量s关于电视广告费用t的回归方程:s=10+3.4*t(单位:万元)
如何确定参数
使用平方误差和衡量预测值与真实值的差距
平方误差真实值y,预测值 ,则平方误差就是 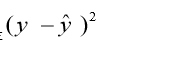
寻找合适的参数,使得平方误差和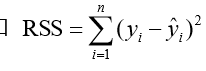 最小。
最小。

使用最小二乘法确定参数:
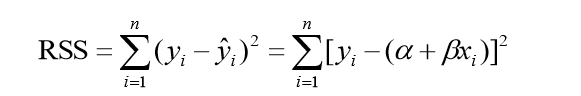
因为要与系数相关,把预测值写成线性回归方程形式。
RSS其实是关于α与β的函数,因为要对RSS取得最小值,所以这里我们分别对α与β求偏导并令偏导等于0,就可以得出α与β的值

把大写看成是总体的
由于总体未知,采用样本值估计:

从而,对于每个xi,我们可以通过 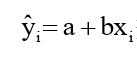 预测相应的y值
预测相应的y值
例子
x=c(1,2,3,4),y=c(6,5,7,10)。构建y关于x的回归方程y=α+βx

使用最小二乘法求解参数:

得到y=3.5+1.4x
如果有新的点x=2.5,则我们预测相应的y值为3.5+1.4*2.5=7
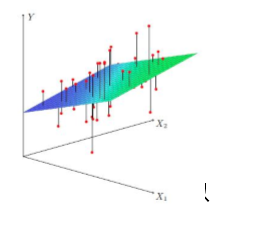
多元线性回归模型
当Y值的影响因素不唯一时,采用多元线性回归模型
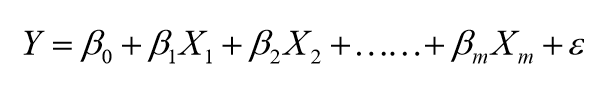
例如商品的销售额可能与电视广告投入,收音机广告投入,报纸广告投入有关系,可以
有
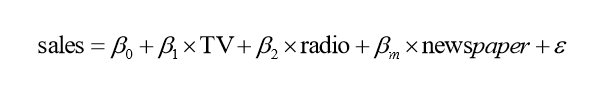
参数估计
最小二乘法:
与一元回归方程的算法相似
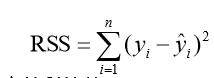 是关于βi的函数。分别对βi求偏导并令偏导等于0,可以解出相应的βi的值
是关于βi的函数。分别对βi求偏导并令偏导等于0,可以解出相应的βi的值
以矩阵的形式书写:
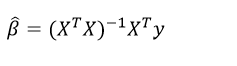
Python实现
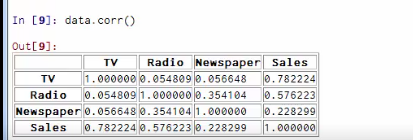
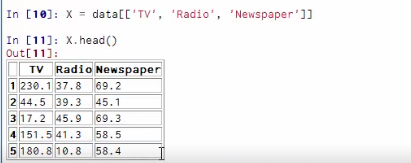
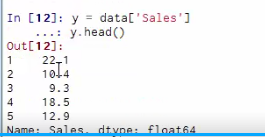
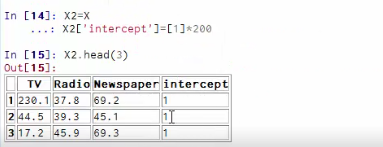
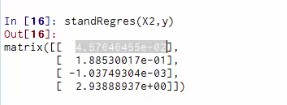
#-*- coding: utf-8 -*- from numpy import * import pandas as pd ###线性回归#### #读取数据,数据在网页上可以下载得到(商品销售额、电视广告投入、收音机广告投入、报纸广告投入) data = pd.read_csv('http://www-bcf.usc.edu/~gareth/ISL/Advertising.csv', index_col=0) #先查看一下数据集的基本情况,看到一共200行数据 data.head() data.tail() #画散点图 import seaborn as sns import matplotlib %matplotlib inline sns.pairplot(data, x_vars=['TV','Radio','Newspaper'], y_vars='Sales', size=7, aspect=0.8) sns.pairplot(data, x_vars=['TV','Radio','Newspaper'], y_vars='Sales', size=7, aspect=0.8, kind='reg') #计算相关系数矩阵 data.corr() #构建X、Y数据集 X = data[['TV', 'Radio', 'Newspaper']] X.head() y = data['Sales'] y.head() ##直接根据系数矩阵公式计算 def standRegres(xArr,yArr): xMat = mat(xArr); yMat = mat(yArr).T xTx = xMat.T*xMat if linalg.det(xTx) == 0.0: print "This matrix is singular, cannot do inverse" return ws = xTx.I * (xMat.T*yMat) return ws #求解回归方程系数,增加截距项 X2=X X2['intercept']=[1]*200 standRegres(X2,y) ##利用现有库求解 from sklearn.linear_model import LinearRegression linreg = LinearRegression() linreg.fit(X, y) print linreg.intercept_ print linreg.coef_ print zip(['TV','Radio','Newspaper'], linreg.coef_) ##测试集和训练集的构建 from sklearn.cross_validation import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1) linreg.fit(X_train, y_train) #结果 print linreg.intercept_ print linreg.coef_ print zip(['TV','Radio','Newspaper'], linreg.coef_) #预测 y_pred = linreg.predict(X_test) #误差评估 from sklearn import metrics #calculate MAE using scikit-learn print "MAE:",metrics.mean_absolute_error(y_test,y_pred) #calculate MSE using scikit-learn print "MSE:",metrics.mean_squared_error(y_test,y_pred) #calculate RMSE using scikit-learn print "RMSE:",np.sqrt(metrics.mean_squared_error(y_test,y_pred)) ##模型比较 feature_cols = ['TV', 'Radio'] X = data[feature_cols] y = data.Sales X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1) linreg.fit(X_train, y_train) y_pred = linreg.predict(X_test) #calculate MAE using scikit-learn print "MAE:",metrics.mean_absolute_error(y_test,y_pred) #calculate MSE using scikit-learn print "MSE:",metrics.mean_squared_error(y_test,y_pred) #calculate RMSE using scikit-learn print "RMSE:",np.sqrt(metrics.mean_squared_error(y_test,y_pred))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
读取数据

散点图

模型构建
– 直接利用公式编写函数
– 利用现有的库

矩阵的行列式,如果等于0,打印这个矩阵是奇异的,不能进行求逆运算。
增加截距项,都是1



构建训练集与测试集,评估模型



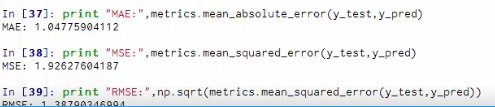
变量选择,模型比较