基于Python的Logistic回归模型_python 多元logistic回归

本文是基于Python的logistic回归模型的建模和分析

一、Logistic原理

1.logistic函数

Logistic函数是讲数据映射到0-1区间的概率值，数据中包含分类的数据（即不连续的数据，如：0,1数据等），表达式如下：

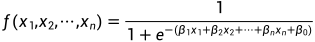
其中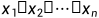，是数据变量，是变量的系数。

2.最大似然函数估计

我们将上式中变量部分定义为，这就是转换为一个线性方程，然后我们就可以通过极大似然估计法对变量系数进行估计和计算，可参考

一元线性回归模型（保姆级）_数据小师弟的博客-CSDN博客

二、代码例子

1. 数据集

数据集如下图，我只截取了部分的数据展示：

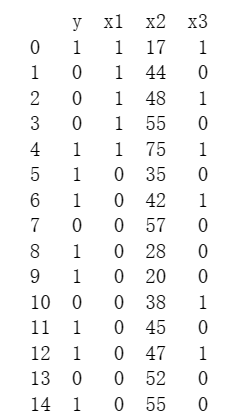
2.代码实现

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
 
X = df.iloc[:, [1,2,3]].values
y = df.iloc[:, 0].values
#划分训练集和测试集，训练集：测试集=8:2
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20, random_state = 0)
#对数据进行特征提取，进行数据标准化
sc_X = StandardScaler()
X_train = sc_X.fit_transform(X_train)
X_test = sc_X.transform(X_test)
 
#Logistic拟合模型
classifier = LogisticRegression(random_state = 0)
classifier.fit(X_train, y_train)
#打印参数结果
print("Logistic参数结果：",classifier.intercept_,classifier.coef_)
 
y_pred = classifier.predict(X_test)
#计算R方
cm = accuracy_score(y_test, y_pred)
 
print("测试集的R方：",cm)

结果如下：

第一个系数是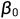，剩下三个参数是变量x1,x2,x3的系数

Logistic参数结果： [-0.21588339] [[-0.80772308 -0.15407737 -0.01698285]]

测试集的R方： 0.4444444444444444

从R方的结果来看，效果并不是很好，我们可以从数据记得划分、改变模型等方法进行优化提高R方数值。

然后画图观察数据的情况，如下：

#设置图表中允许显示中文
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] =False #减号unicode编码
 
fig, ax = plt.subplots(figsize=(10, 6))
plt.title("测试y与预测y散点图")
plt.xlabel("点数")#x轴标签
plt.ylabel("预测y与测试y")#y轴标签
ax.plot(y_test, 'o',c = '#00CED1', label='y_test',markersize=8)
ax.plot(y_pred,'o', c = '#DC143C',label='y_pred',markersize=4)
plt.legend()
print("测试结果：",y_test)
print("预测结果：",y_pred)

结果如下：

测试结果： [0 0 0 1 0 1 1 1 1 1 0 1 0 0]

预测结果： [1 0 1 0 1 1 1 1 0 1 1 0 0 0]

三、参考资料

sklearn文档
Logistic公式推导