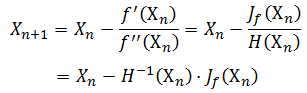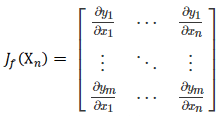- 1OpenGL ES 3.0 开发(十八):相机 LUT 滤镜_3d lut opengl shader
- 2linux 创建开机自动启动python脚本_linux python项目开机自启动
- 3ADB 命令 模拟按键 keyevent keycode_adb keyevent
- 4leetcode 452.用最少数量的箭引爆气球 贪心法求解 (c++版本)_how to get only integer using fractional number in
- 5centos上根据进程号 查找启动文件目录_centos7通过pid查找文件
- 6Ubuntu 安装 MySQL 8.0+
- 7DruidDataSource常用配置_com.alibaba.druid.pool.preparedstatementpool.close
- 8阿里云发布全新开源操作系统『龙蜥』,支持 X86 64 和 ARM 64 架构及鲲鹏、飞腾等芯片...
- 9java mysql数据库连接池DruidPool配置及表操作实现方法_java mysql连接池
- 10Linux查询日志命令
牛顿法与Hessian矩阵
赞
踩
牛顿法 主要有两方面的应用:
1. 求方程的根;
2. 求解最优化方法;
一. 为什么要用牛顿法求方程的根?
问题很多,牛顿法 是什么?目前还没有讲清楚,没关系,先直观理解为 牛顿法是一种迭代求解方法(Newton童鞋定义的方法)。
假设 f(x) = 0 为待求解方程,利用传统方法求解,牛顿法求解方程的公式:
f(x0+Δx) = f(x0) + f′(x0) Δx
即 f(x) = f(x0) + f′(x0) (x-x0)
公式可能大家会比较熟悉,一阶泰勒展式,f′(a) 表示 f(x) 在 x0 点的斜率 (这个很好理解),当X方向增量(Δx)比较小时,Y方向增量(Δy)可以近似表示为 斜率(导数)*X方向增量(f′(x0) Δx) ,令 f(x) = 0,我们能够得到 迭代公式:
x = x0 - f(x0) / f′(x0) => xn+1 = xn - f(xn) / f′(n)
通过逐次迭代,牛顿法 将逐步逼近最优值,也就是方程的解。
二. 扩展到最优化问题
这里的最优化 是指非线性最优化,解非线性最优化的方法有很多,比如 梯度下降法、共轭梯度法、变尺度法和步长加速法 等,这里我们只讲 牛顿法。
针对上面问题进行扩展:
解决 f(x) = 0 的问题,我们用了一阶泰勒展开:
f(x) = f(x0) + f'(x0)*(x-x0) + o( (x-x0)^2 )
去掉末位高阶展开项,代入x = x0+Δx,得到:
f(x) = f(x0+Δx) = f(x0) + f′(x0) Δx
那么 要解决 f′(x) = 0 的问题,我们就需要二阶泰勒展开:
f(x) = f(x0) + f'(x0)*(x-x0) + 0.5*f''(x0)*(x-x0)^2 + o( (x-x0)^3 )
去掉末位高阶展开项,代入x = x0+Δx,得到:
f(x) = f(x0+Δx) = f(x0) + f′(x0)Δx + 0.5 * f′′(x0) (Δx)^2
求导计算: f′(x) = f'(x0+Δx) = 0,得到:
[ f(x0) + f′(x0)(x−x0) + 0.5 f′′(x0)(x−x0)^2 ]′ = 0
整理:
f′(x0) + f′′(x0)(x−x0) = 0
x = x0 − f′(x0) / f′′(x0) => xn+1 = xn - f'(xn) / f'′(xn)
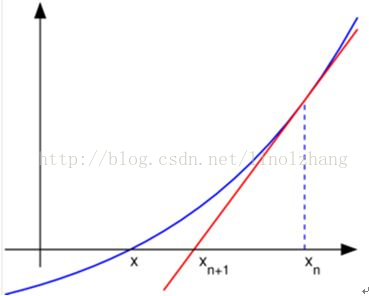
牛顿法 一图总结为:
三. 牛顿法 与 Hessian矩阵的关系
以上牛顿法的推导 是针对 单变量问题,对于多变量的情况,牛顿法 演变为:
与上面的单变量表示方式类似,需要用到变量的 一阶导数 和 二阶导数。
其中 J 定义为 雅克比矩阵,对应一阶偏导数。
H 为 Hessian矩阵,对应二阶偏导数。
网上也能搜到类似的公式表达,也列出来:
牛顿法 在多变量问题上仍然适用迭代求解,但Hessian矩阵的引入增加了复杂性,特别是当:
▪ Hessian 矩阵非正定(非凸)导致无法收敛;
▪ Hessian 矩阵维度过大带来巨大的计算量。
针对这个问题,在 牛顿法无法有效执行的情况下,提出了很多改进方法,比如 拟牛顿法(Quasi-Newton Methods)可以看作是牛顿法的近似。
拟牛顿法 只需要用到一阶导数,不需要计算Hessian矩阵 以及逆矩阵,因此能够更快收敛,关于 拟牛顿法 这里不再具体展开,也有更深入的 DFP、BFGS、L-BFGS等算法,大家可以自行搜索学习。
总体来讲,拟牛顿法 都是用来解决 牛顿法 本身的 复杂计算、难以收敛、局部最小值等问题。