强化学习算法_强化学习中加速度和角速度的离散化都具体怎么做的?比如角速度在[0,359]范围内

作者：Cpp五条 | 2024-05-30 22:39:50

踩

强化学习中加速度和角速度的离散化都具体怎么做的?比如角速度在[0,359]范围内

强化学习算法

游戏模型如下：
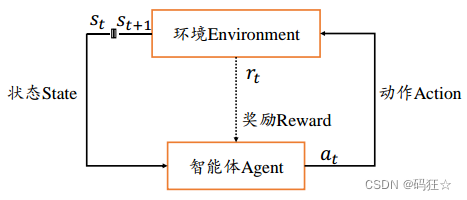
在这里插入图片描述

策略网络输入状态s，输出动作a的概率分布如下： $\pi(a|s)$

多次训练轨迹如下

r表示回报
横轴为T, 1个回合的步骤数
纵轴为N, 回合数，1行代表1条轨迹，符合概率分布P

[\begin{matrix} s_{11} a_{11} r_{11} \dots \dots s_{1 t} a_{1 t} r_{1 t} \dots \dots s_{1 T} a_{1 T} r_{1 T} \\ \dots \dots \dots \dots \dots \dots \\ s_{n 1} a_{n 1} r_{n 1} \dots \dots s_{n t} a_{n t} r_{n t} \dots \dots s_{n T} a_{n T} r_{n T} \\ \dots \dots \dots \dots \dots \dots \\ s_{N 1} a_{N 1} r_{N 1} \dots \dots s_{N t} a_{N t} r_{N t} \dots \dots s_{N T} a_{N T} r_{N T} \end{matrix}]

$\begin{bmatrix} s_{11} a_{11} r_{11} …… s_{1t} a_{1t} r_{1t} …… s_{1T} a_{1T} r_{1T}\\ …… …… ……\\ s_{n1} a_{n1} r_{n1} …… s_{nt} a_{nt} r_{nt}…… s_{nT} a_{nT} r_{nT} \\ …… …… ……\\ s_{N1} a_{N1} r_{N1} …… s_{Nt} a_{Nt} r_{Nt} …… s_{NT} a_{NT} r_{NT}\\ \end{bmatrix}$

s_{11} a_{11} r_{11} \dots\dots s_{1 t} a_{1 t} r_{1 t} \dots\dots s_{1 T} a_{1 T} r_{1 T} \dots\dots\dots\dots\dots\dots s_{n 1} a_{n 1} r_{n 1} \dots\dots s_{n t} a_{n t} r_{n t} \dots\dots s_{n T} a_{n T} r_{n T} \dots\dots\dots\dots\dots\dots s_{N 1} a_{N 1} r_{N 1} \dots\dots s_{Nt} a_{Nt} r_{Nt} \dots\dots s_{NT} a_{NT} r_{NT}

策略轨迹 $\tau = s_{1} a_{1} , s_{2} a_{2}，……，s_{T} a_{T}$

发生的概率
$P(\tau) = P(s_{1} a_{1} , s_{2} a_{2}，……，s_{T} a_{T})$
$P(s_{1})\pi(a_{1}|s_{1})P(s_{2}|s_{1},a_{1})\pi(a_{2}|s_{2})P(s_{3}|s_{1},a_{1},s_{2},a_{2})……$
$P(s_{1})\prod_{t=1}^{T-1}\pi(a_{t}|s_{t})P(s_{t+1}|s_{1},a_{1},......,s_{t},a_{t})$

根据马尔科夫性(Markov Property)，简化为：
$P(\tau) = P(s_{1})\prod_{t=1}^{T-1}\pi(a_{t}|s_{t})P(s_{t+1}|s_{t},a_{t})$

奖励

在每次智能体与环境的交互过程中，均会得到一个滞后的奖励
$r_{t} = r(s_{t},a_{t})$

一次交互轨迹

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/Cpp五条/article/detail/648941