现代信号处理——参数估计理论（最小二乘估计）_加权最小二乘估计

Bayes估计需要知道被估计量的先验概率密度；最大似然估计需要知道似然函数。

除了线性均方估计外，最小二乘估计是另一种不需要任何先验知识的参数估计方法，最小二乘估计不需要先验统计特性，适用范围更广。

一、最小二乘估计

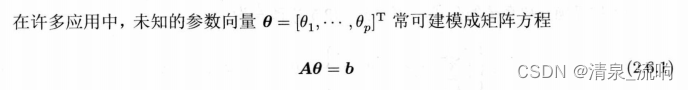
式中A和b分别是与观测数据有关的系数矩阵和向量，它们是已知的。这一数学模型包括以下三种情况：

（1）未知参数的个数与方程个数相等，且矩阵A非奇异。此时，矩阵方程(2.6.1）称为适定方程(well-determined equation),存在唯一解θ=A^(-1)b;

（2）矩阵A是一“高矩阵”(行数多于列数），即方程个数多于未知参数个数。此时，矩阵方程(2.6.1)称为超定方程(overdetermined equation)； 

（3）矩阵A是一“扁矩阵”(行数少于列数），即方程个数少于未知参数个数。此时，矩阵方程(2.6.1)称为欠定方程(underdetermined equation)。

 

 最小二乘估计的代价函数为：

所以，最小二乘估计量，是满足下述方程的解： 

 

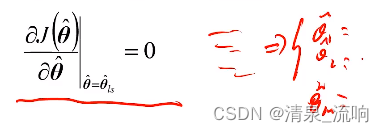
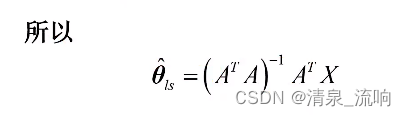
这一方程有两类不同的解：

（1）矩阵A满列秩时，由于(A^T)A非奇异，最小二乘估计由

 

 唯一确定，此时称参数向量θ是唯一可辨识的。

(2)矩阵A秩亏缺时，由不同的θ值均能得到相同的Aθ值。因此，虽然向量b可以提供有关Aθ的某些信息，但我们却无法区别对应于同一Aθ值的各个不同的θ值。在这个意义上，称参数向量θ是不可辨识的。更一般地讲，如果某参数的不同值给出在抽样空间上的相同分布，则称这一参数是不可辨识的。

若观测噪声n的均值矢量为零，则最小二乘估计的均方误差为： 

 例：根据以下对二维矢量θ的两次观测，求0的最小二乘估计。

 

 

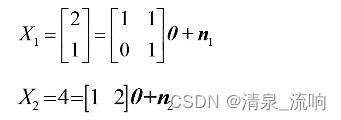
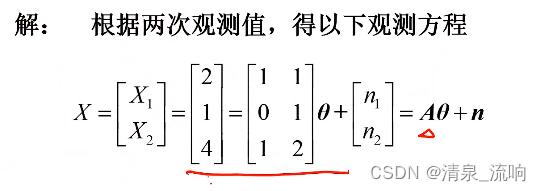
二、加权最小二乘估计

当误差向量e的各分量不仅具有相同的方差，而且还不相关时，最小二乘估计具有最小的估计方差 ，因而是最优的。如果误差向量各分量具有不同的方差，或者各分量之间相关时，最小二乘估计就不再具有最小的估计方差，因而不会是最优的。那么，在这样的情况下，如何求出具有最小方差的估计子呢?为了克服最小二乘估计的这一缺陷，考虑对其损失函数——误差平方和进行改造：使用“加权误差平方和”作为新的损失函数

提出背景：如果各次观测误差的不同，所得的各次观测量的精度也是不同的。

误差方差小时，观测量的精度较高，误差方差大时，观测量的精度较低。

如何在构造估计量时，综合考虑上述因素？

可以通过加权的方式，提高估计的精确度——加权最小二乘估计，其代价函数为：

 

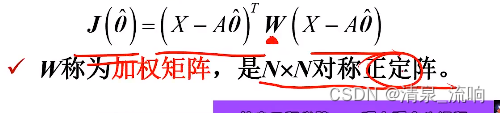
加权最小二乘估计量满足下述方程： 

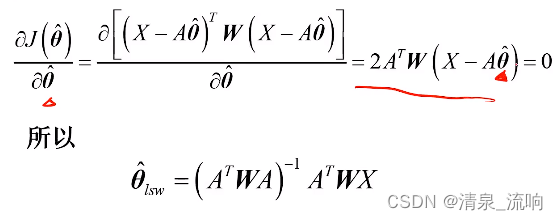
加权最小二乘估计矢量的均方误差为：

 

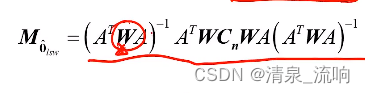
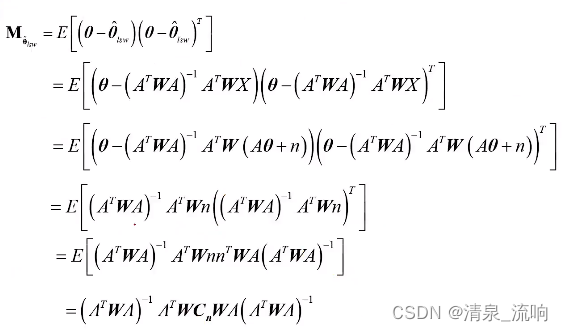
 若观测噪声矢量n的均值矢量为零，协方差矩阵为Cn，则最优的加权矩阵为：

估计量为：

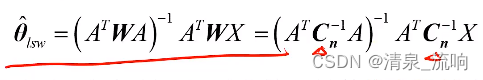
此时，加权最小二乘估计矢量的均方误差为：

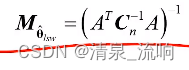
 例：用电表对电压进行两次测量，测量结果分别为216V和220V，观测方程为

216=θ+n1；220=θ+n2

其中，观测噪声矢量的均值矢量和协方差矩阵分别为

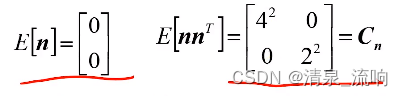
求电压的最小二乘估计和加权最小二乘估计，并对结果进行比较和讨论。 

 

 

 参考视频与文献：

https://www.bilibili.com/video/BV1wS4y1D7ng?p=4&vd_source=77c874a500ef21df351103560dada737

现代信号处理（第三版）张贤达（编著）