Gausst松鼠会

这个屌丝很懒，什么也没留下！

热门标签

最详细的SVM数学模型讲解_svm一般需要多少组数据

作者：Gausst松鼠会 | 2024-03-23 06:08:11

踩

svm一般需要多少组数据

背景：

支持向量机SVM常用于二分类问题，其输入的数据形式如[x1,x2,x3...,xn,y]，其中x1,x2,...,xn为特征值，y为结果值，为1和-1。

点到直线的距离：

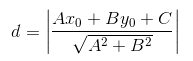
点到超平面的距离：

$d=\frac{\left | \alpha ^{T}x+\beta \right |}{\left \| \alpha \right \|}$

如果只有两个特征值，则数据形式为[x1,x2,y]，举个详细的例子如下：

[1,1,-1]

[1,2,-1]

[1,4,1]

[3,3,1]

四组数据，两正两负，可以发现这是一个二维的数据，因此可以画一个二维的坐标系去展示，如下图所示。

SVM就是选择一个超平面，将y=1和y=-1的数据分开，在二维数据的情况下，这个超平面就是一条直线，如下图中绿色的线所示。

如果是三维数据，则可以发现这个超平面是一个平面。

如上面所说，SVM是为了选出一个超平面将y=1和y=-1的数据分开，那么得到这个超平面的步骤是什么？

假设这个超平面的数学公式为 $\alpha _{1}x_{1}+\alpha _{2}x_{2}+...\alpha _{n}x_{n}+\beta =0$ ，另一种形式为 $\alpha ^{T}x+\beta =0$ ， $\alpha$ 是一个向量 $[\alpha _{1},\alpha _{2},...,\alpha _{n}]$

x也代表一个向量 $[x_{1},x_{2},...,x_{n}]$ 。我们可以发现，下图中的绿色直线有很多，肯定不止上面图中所绘的那一条，那么如何选择最好的呢，我们假设所有能将y=1和y=-1的数据分开的超平面的集合称为解空间。如下a,b,c三个超平面都可以划分成功，但是可以看到b直线没有非常的靠近某一个点。

SVM的目标：在解空间中选择一个解，也就是一个超平面，计算出所有点中到超平面最近的点到超平面的距离，每个超平面计算出一个。然后不断的选择超平面，计算最近距离。然后再从上面所有的最近距离中，选出最大的距离所对应的超平面M。此时超平面M就是SVM的目标。数学表达为

$M=arg_{\alpha ,\beta } max(min(\frac{\left | \alpha ^{T}x+\beta \right |}{\left \| \alpha \right \|}))$

其实上面部分描述的是理想状态下，需要满足y=1和y=-1的分离完全正确。如果y=1和y=-1的数据分离的不完全正确，如下图所示，红点和蓝点不能完全分开，所以如果按上面讨论的方法，求出各个超平面最近距离没有意义，因为有的红点划分到了蓝点的区域。

所以必须得选择划分正确的点。所以上面的公式要变成

$M=arg _{\alpha ,\beta }max(min((\frac{y( \alpha ^{T}x+\beta )}{\left \| \alpha \right \|})>0))$

只有在 $y( \alpha ^{T}x+\beta )$ >0时，点的划分才是正确的。

此时可以得到一个数学模型：

$M=arg_{\alpha ,\beta }max(min(\frac{1}{||\alpha ||}y( \alpha ^{T}x+\beta )))$

s.t. $y( \alpha ^{T}x+\beta )>0$

下面对这个数学模型进行简化，令 $min(y( \alpha ^{T}x+\beta ))=1$ ，则可以简化为

$M=arg_{\alpha ,\beta }max(\frac{1}{||\alpha ||})$

s.t. $y( \alpha ^{T}x+\beta )\geqslant 1$

为什么可以令 $min(y( \alpha ^{T}x+\beta ))=1$ ，因为

$min(\frac{1}{||\alpha ||}y( \alpha ^{T}x+\beta ))\rightarrow \frac{1}{||\alpha ||}min(y( \alpha ^{T}x+\beta ))$

所以可以发现无论 $y( \alpha ^{T}x+\beta )$ 缩放多少，其对应的最小值点都是固定的，因此做简化可以令 $min(y( \alpha ^{T}x+\beta ))=1$ 。其真实的含义就是令所有超平面下，离超平面最近的点的距离都是 $\frac{1}{||\alpha ||}$ 。那么条件公式为 $\frac{y( \alpha ^{T}x+\beta )}{\left \| \alpha \right \|} \geqslant \frac{1}{||\alpha ||}\rightarrow y( \alpha ^{T}x+\beta )\geqslant 1$ 。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/Gausst松鼠会/article/detail/293537