小朋友都能看懂的K-SVD算法_k-svd 图解

稀疏表达与字典学习模型（综合模型）

假设有一系列的样本 { y ⃗ i ∣ y ⃗ i ∈ R n } i = 1 N \{\vec{y}_i| \vec{y}_i\in \mathbb{R}^{n}\}_{i=1}^{N} {y ​i​∣y ​i​∈Rn}i=1N​，我们想要学一个字典$\mathbf{D}\in {\mathbb{R}}^{n\times K}$，这个字典有$K$个原子 { d ⃗ k } k = 1 K \{\vec{d}_k\}_{k=1}^K {d k​}k=1K​，用这些原子可以线性组合成所有的样本来。故每个样本${\vec{y}}_i$都有其对应的稀疏系数${\vec{x}}_i\in {\mathbb{R}}^K$，即：
y ⃗ i = D x ⃗ i , which is equal to  y ⃗ i = ∑ j = 1 K d ⃗ j ⋅ x j , i .

$$\begin{aligned} \vec{y}_i &= \mathbf{D} \vec{x}_i,\\ \text{which is equal to }\vec{y}_i &= \sum_{j=1}^{K} \vec{d}_{j} \cdot x_{j,i}. \end{aligned}$$ y ​i​which is equal to y ​i​​=Dx i​,=j=1∑K​d j​⋅xj,i​.​
那么，对于整个样本集来说，就有如下的字典学习模型：
$$\mathbf{Y}=\mathbf{DX}.$$

而稀疏性指的是，只选取很少的字典原子，就能够组合成一个样本：
$$\text{for each }i,\text{ we have }\Vert {\vec{x}}_i{\Vert }_0\le T_0.$$
要满足这个要求，我们学到的字典原子要尽可能地不相关，即$⟨{\vec{x}}_{i_1},{\vec{x}}_{i_2}⟩$尽可能大。

小结一波，所以说，我们的优化目标如下：
$$\underset{\mathbf{D},\mathbf{X}}{\min }\Vert \mathbf{DX}-\mathbf{Y}\Vert ,\text{ subject to }\forall i,\Vert {\vec{x}}_i{\Vert }_0\le T_0.$$

形象例子1

为了帮助大家理解，我举一个形象的例子。

单个样本的稀疏表示${\vec{y}}_i=\mathbf{D}{\vec{x}}_i$本质上和下面的事件等价：

假设，有$N$个人去超市买东西，每个人都写好了自己的购物清单。超市里一共有$K$款商品 { d ⃗ k } k = 1 K \{\vec{d}_k\}_{k=1}^K {d k​}k=1K​（每款数量充足）。

第$i$个人进来了，他购物清单${\vec{x}}_i$上写着：第1款商品要$x_{1,i}$件，第2款商品要$x_{2,i}$件，……，第K款商品要$x_{K,i}$件。他就根据这张单子将想要的东西放进自己的篮子里，然后结算离开。

那么我们要学习一个怎么样的字典$\mathbf{D}$才能满足要求呢？

答案是显而易见的，就是我们商店中拥有的商品要满足这$N$个顾客的需求。

用数学的形式来说，就是我们要学一个过完备(overcomplete)字典，$K>>N$，用字典中的这$K$个原子就已经能够线性组合出所有的样本来。

那么稀疏性在这个例子中怎么体现呢？

其实这也跟我们日常生活中的购买习惯是类似的。就算一个人的购买力很强，去商店中也只是买到占商店商品种类数很少的商品。（当然，不排除有博主，为了拍视频去把商店中的所有商品全部买回来-_-!!!）

字典学习模型的另一种表现形式

在真正讲K-SVD模型之前，我们还需要补充字典学习模型的另一种数学表示。

先回顾一下最基本的字典学习模型：$$\mathbf{Y}=\mathbf{DX},$$其中$\mathbf{Y}$是样本集，$\mathbf{D}$是字典，$\mathbf{X}$是稀疏编码矩阵。

稀疏编码矩阵也可以用如下形式来表示，其中${\mathrm{x}}_{\mathrm{T}}^{\mathrm{k}}$表示$\mathbf{X}$的第k行。：
X = [ x T 1 x T 2 ⋮ x T K ] . \mathbf{X} =

$$\begin{bmatrix} \rm{x}_T^1\\ \rm{x}_T^2\\ \vdots \\ \rm{x}_T^K\end{bmatrix}$$ . X= ​xT1​xT2​⋮xTK​​ ​.

字典学习模型的另一种表现形式如下：
Y = ∑ k = 1 K d ⃗ k x T k , here  d ⃗ k x T k = [ x k , 1 ⋅ d ⃗ k , x k , 2 ⋅ d ⃗ k , ⋯   , x k , N ⋅ d ⃗ k ] .

$$\begin{aligned} \mathbf{Y} &= \sum_{k=1}^K \vec{d}_k \rm{x}_T^k,\\ \text{here }\vec{d}_k\rm{x}_T^k &= \begin{bmatrix}x_{k,1}\cdot \vec{d}_k,&x_{k,2}\cdot \vec{d}_k,&\cdots, &x_{k,N}\cdot \vec{d}_k\end{bmatrix}. \end{aligned}$$ Yhere d k​xTk​​=k=1∑K​d k​xTk​,=[xk,1​⋅d k​,​xk,2​⋅d k​,​⋯,​xk,N​⋅d k​​].​
这相当于将${\vec{d}}_k$加权后分别赋给对$N$个样本的表示。

形象例子2

这种表现形式对于一般人来说有点抽象，但是也可以用上面的例子的变体来形象的理解。

不知道大家有没有在美团买菜、叮咚买菜等APP上下单，然后由负责人送货上门的经历：假设，有$N$个人在APP上下单，每个人都有自己的购物清单。APP中一共有$K$款商品 { d ⃗ k } k = 1 K \{\vec{d}_k\}_{k=1}^K {d k​}k=1K​供用户挑选（每款数量充足）。

第k项${\vec{d}}_k{\mathrm{x}}_{\mathrm{T}}^{\mathrm{k}}$本质上和下面的事件等价：

负责人进行商品分拣时，他拿到的是按照商品排序的总单（P.S.: 因为通常同种商品会放在一起，按商品排序的总单对于负责人来说，更加方便分拣）

负责人定位到总单中第k款商品，第1个顾客要$x_{k,1}$件，第2个顾客要$x_{k,2}$件，……，第N个顾客要$x_{k,N}$件。他先按照单子将第k款商品放到各个用户的篮子里，再分第k+1款商品。

SVD分解（奇异值分解）

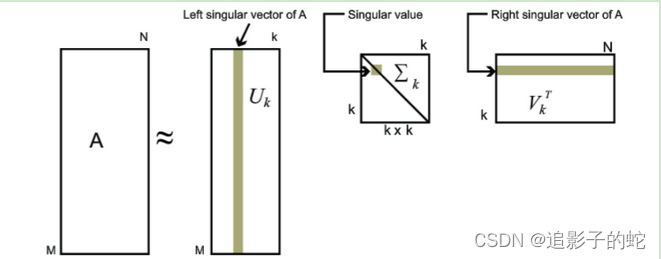
矩阵$\mathbf{A}\in {\mathbb{R}}^{m\times n}$，能够分解成$\mathbf{A}=\mathbf{U\Sigma }{\mathbf{V}}^T$。其中$\mathbf{U}$和$\mathbf{V}$都是酉矩阵，即满足${\mathbf{U}}^T\mathbf{U}=\mathbf{I},{\mathbf{V}}^T\mathbf{V}=\mathbf{I}$且$\Vert {\vec{u}}_i{\Vert }_2=1,\Vert {\vec{v}}_i{\Vert }_2=1$。$\mathbf{\Sigma }$为对角矩阵，对角元素为$\mathbf{A}$的特征值（奇异值${\sigma }_1,{\sigma }_2,\cdots$呈单调递减排列）

也就是说，$\mathbf{A}$可以等价于若干组特征向量的线性叠加：
$$\mathbf{A}=\sum _{i=1}^k{\sigma }_i{\vec{u}}_i\cdot {\vec{v}}_i^T.$$看下面这个图就能有更加清晰的认知：

如何求解奇异值矩阵$\mathbf{\Sigma }$和特征向量矩阵$\mathbf{U}$、$\mathbf{V}$的值？

对$\mathbf{A}{\mathbf{A}}^T$和${\mathbf{A}}^T\mathbf{A}$做特征分解即可。

$\mathbf{A}{\mathbf{A}}^T=\mathbf{U}{\mathbf{\Sigma }}^2{\mathbf{U}}^T$
${\mathbf{A}}^T\mathbf{A}=\mathbf{V}{\mathbf{\Sigma }}^2{\mathbf{V}}^T$

MATLAB做SVD分解：

[U,S,V] = SVD(A,'econ') % A=U*S*V'
1

python做SVD分解：

import numpy as np
[U,S,VT] = np.linalg.svd(A, full_matrices=0) # A=U*S*VT
1
2

K-SVD算法

使用K-SVD算法来更新如下模型：
$$\underset{\mathbf{D},\mathbf{X}}{\min }\Vert \mathbf{DX}-\mathbf{Y}\Vert ,\text{ subject to }\forall i,\Vert {\vec{x}}_i{\Vert }_0\le T_0.$$

• 原理：K-SVD算法想要同时更新$d_k$和${\mathrm{x}}_{\mathrm{T}}^{\mathrm{k}}$（这个时候认为 { d j } j ≠ k \{d_j\}_{j\neq k} {dj​}j=k​和 { x T j } j ≠ k \{\rm{x}_T^j\}_{j\neq k} {xTj​}j=k​是固定不变的）。从$k=1$到$k=K$，共update K次，完成一次对于整个字典及对应稀疏矩阵的更新。一共更新若干次整个字典及稀疏矩阵。

• 具体计算：

  • 首先，将问题转化：

  min ⁡ d ⃗ k , x T k ∥ D X − Y ∥ F 2 = min ⁡ d ⃗ k , x T k ∥ Y − ∑ j = 1 K d ⃗ j x T j ∥ F 2 = min ⁡ d ⃗ k , x T k ∥ ( Y − ∑ j ≠ k d ⃗ j x T j ) − d ⃗ k x T k ∥ F 2 = min ⁡ d ⃗ k , x T k ∥ E k − d ⃗ k x T k ∥ F 2

  $$\begin{aligned} &\min_{\vec{d}_k, \rm{x}_T^k}\Vert \mathbf{D}\mathbf{X} - \mathbf{Y} \Vert_F^2 \\=&\min_{\vec{d}_k, \rm{x}_T^k} \Vert \mathbf{Y} - \sum_{j=1}^K \vec{d}_j \rm{x}_T^j \Vert_F^2 \\= &\min_{\vec{d}_k, \rm{x}_T^k}\Vert (\mathbf{Y} - \sum_{j\neq k} \vec{d}_j \rm{x}_T^j) - \vec{d}_k \rm{x}_T^k \Vert_F^2\\=&\min_{\vec{d}_k, \rm{x}_T^k}\Vert \mathbf{E}_k - \vec{d}_k \rm{x}_T^k \Vert_F^2 \end{aligned}$$ ===​d k​,xTk​min​∥DX−Y∥F2​d k​,xTk​min​∥Y−j=1∑K​d j​xTj​∥F2​d k​,xTk​min​∥(Y−j=k∑​d j​xTj​)−d k​xTk​∥F2​d k​,xTk​min​∥Ek​−d k​xTk​∥F2​​

  这个时候，我们如果直接对${\mathbf{E}}_k$做SVD分解（不施加任何约束），那么会导致求出来的${\mathrm{x}}_{\mathrm{T}}^{\mathrm{k}}$不稀疏，进而导致 { x ⃗ i } i = 1 N \{\vec{x}_i\}_{i=1}^N {x i​}i=1N​不稀疏，这不是我们想看到的。

  为了在训练过程中让系数逐渐稀疏，作者使用了一个简单但有效的手段，在更新$d_k$和${\mathrm{x}}_{\mathrm{T}}^{\mathrm{k}}$时，引入一个集合 ω k = { i ∣ 1 ≤ i ≤ N , x k , i ≠ 0 } \omega_k = \{i|1\leq i \leq N,x_{k,i}\neq0\} ωk​={i∣1≤i≤N,xk,i​=0}将选用原子$d_k$进行线性组合的样本索引值构成一个集合。

  ${\omega }_k$又对应了一个对角矩阵${\mathbf{\Omega }}_k\in {\mathbb{R}}^{N\times |{\omega }_k|}$：$\text{if }j\in {\omega }_k,{\mathbf{\Omega }}_k(j,j)=1$。矩阵${\Omega }_k$的作用是对原来的矩阵进行瘦身，将不选用原子$d_k$进行线性组合的样本列删除。

  • 所以，我们又可以将问题进行如下的变形：

  min ⁡ d ⃗ k , x T k ∥ E k − d ⃗ k x T k ∥ F 2 = min ⁡ d ⃗ k , x T k ∥ E k Ω k − d ⃗ k x T k Ω k ∥ F 2 min ⁡ d ⃗ k , x T k ∥ E k R − d ⃗ k x R k ∥ F 2

  $$\begin{aligned}&\min_{\vec{d}_k, \rm{x}_T^k}\Vert \mathbf{E}_k - \vec{d}_k \rm{x}_T^k \Vert_F^2 \\ = &\min_{\vec{d}_k, \rm{x}_T^k}\Vert \mathbf{E}_k \mathbf{\Omega}_k- \vec{d}_k \rm{x}_T^k \mathbf{\Omega}_k \Vert_F^2 \\ &\min_{\vec{d}_k, \rm{x}_T^k}\Vert \mathbf{E}_k^R - \vec{d}_k \rm{x}_R^k \Vert_F^2 \end{aligned}$$ =​d k​,xTk​min​∥Ek​−d k​xTk​∥F2​d k​,xTk​min​∥Ek​Ωk​−d k​xTk​Ωk​∥F2​d k​,xTk​min​∥EkR​−d k​xRk​∥F2​​

  现在就可以直接对${\mathbf{E}}_k^R$做SVD分解，有${\mathbf{E}}_k^R=\mathbf{U\Delta }{\mathbf{V}}^T$。用占比最大的一组奇异值和特征向量来近似$d_k$和${\mathrm{x}}_{\mathrm{T}}^{\mathrm{k}}$。

  为了让每个$d_k$的能量尽可能平衡，赋值情况如下：

  d k : = u ⃗ 1 x T k : = σ 1 v ⃗ 1 T

  $$\begin{aligned}d_k &:=\vec{u}_1 \\ \rm{x}_T^k&:=\sigma_1 \vec{v}_1^T\end{aligned}$$ dk​xTk​​:=u 1​:=σ1​v 1T​​