布隆过滤器原理和使用_lsm使用bloom

LSM读放大问题背景

LSM树中读放大的来源是，我们必须寻址多个磁盘驻留表，以便完成读取操作。这是因为我们不一定能预先知道一个磁盘驻留表是否包含要搜索的键指向的数据记录。

LSM使用bloomfilter减少数据扫描

防止表查询的方法之一是在元数据中存储其键的范围（存储给定表中的最小和最大键），并检查要搜索的键是否在该表的范围之内。这一信息是不精确的，它只能告诉我们数据记录是否可能会出现在表中。为了改进这种情况，包括Apache Cassandra和RocksDB在内的许多实现都使用一种称为布隆过滤器（Bloom Filter）的数据结构。

基于概率模型的数据搜索【布隆过滤器（用于集合成员判断）、HyperLogLog（用于估计基数)和Count-Min Sketch】

概率型数据结构通常比它对应的“常规”数据结构具有更高的空间效率。例如，要检查集合成员身份、基数（找出集合中不同元素的数量）或频率（找出某个元素出现的次数），我们必须储存所有集合元素，然后遍历整个数据集以找到结果。而概率结构则允许我们储存近似信息并执行查询，从而产生带有不确定因素的结果。关于这类数据结构的一些众所周知的例子有布隆过滤器（用于集合成员判断）、HyperLogLog（用于估计基数）和Count-Min Sketch。

布隆过滤器概念

隆过滤器是Burton Howard Bloom在1970年提出的，它是一种空间效率很高的概率型数据结构，可以用来测试元素是否是集合的成员。它可能产生假阳性匹配（返回“元素在集合中”的结果，而实际上该元素却不在集合中），但不会出现假阴性匹配（若返回“元素不在集合中”的结果，则保证该元素肯定不是集合的成员）。

布隆过滤器原理

换句话说，可以使用布隆过滤器来判断键是否可能在表中或肯定不在表中。在查询期间跳过布隆过滤器返回“不匹配”的文件，而只访问其余文件，以查明数据记录是否确实存在。使用与磁盘驻留表相关联的布隆过滤器能显著减少读取过程中要访问的表的数量。
布隆过滤器使用一个大的比特数组和多个哈希函数构建。将这些哈希函数应用于表中记录的键，并将哈希值作为数组下标来将其对应比特位设置为1。如果哈希函数所确定的所有比特位都为1，则表示该搜索键在该集合中可能是存在的。
在查找过程中，当检查布隆过滤器中的元素是否存在时，需要再次计算键的哈希函数：如果所有哈希函数确定的位都为1，则返回肯定的结果，说明该项目有一定概率是集合中的成员；如果至少有一个位为0，则我们可以肯定地说该元素不存在于集合中。
应用于不同键的哈希函数可能返回相同的比特位并导致哈希冲突，比特位为1仅表示某个哈希函数为某个键产生了该比特位上的一个置位。

如何提高布隆过滤器的准确度？

假阳性的概率是通过配置比特集的大小和哈希函数的数量来控制的：在较大的比特集中，冲突的概率较小；同样，若拥有更多的哈希函数，则我们也可以检查更多的比特位，这也将产生一个更精确的结果。较大的比特集占用较多的内存，而用较多的哈希函数计算结果又可能会对性能产生负面影响，因此我们必须在可接受的概率和产生的开销之间进行权衡。概率可以从预期的集合大小中计算出来。因为LSM树中的表是不可变的，所以集合大小（表中键的数目）是预先知道的。

布隆过滤器实战

布隆过滤器数据写入

让我们来看一个简单例子，我们有一个16位的比特数组和3个哈希函数，它们产生key1的值3、5和10。我们现在在这些位置上设置比特位。添加下一个键，用哈希函数产生key2的值5、8和14，我们也为key2设置比特位。

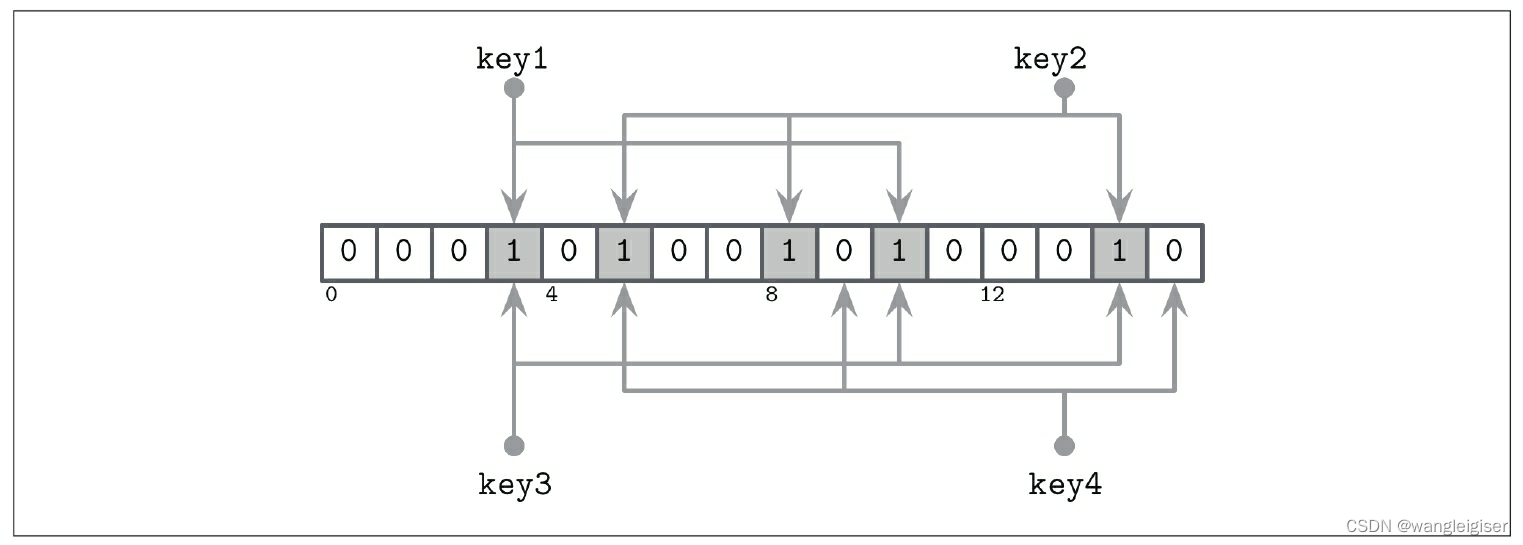
一个假阳性的例子:数据可能存在集合中

现在，我们尝试检查key3是否存在于集合中，用哈希函数生成3、10和14。由于在添加key1和key2时所有三个位都被置位，所以我们会遇到这样一种情况，即布隆过滤器返回一个假阳性报告：key3从未被添加到那里，但所有被计算的位都被置位。但是，由于布隆过滤器只声明元素可能在表中，所以这个结果是可以接受的。

一个真阴性的例子：数据一定不在集合中

如果我们尝试查找key4并由哈希函数得到值5、9和15，那么我们会发现只有第5位被置位，而其他两位未置位。即使只有其中一位未置位，我们也可以肯定该元素从未被添加到过滤器中。