devbox
Gausst松鼠会
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

手把手教数据结构与算法：栈的应用（平衡符号和简单计算器）_计算器系统 栈

作者：Gausst松鼠会 | 2024-06-16 23:53:16

赞

踩

计算器系统 栈

个人主页：

想转码的电筒人

专栏：

手把手教数据结构与算法

目录

栈

基本概念

栈的定义

栈的特点

栈的常见基本操作

栈的应用

问题一：平衡符号

题目描述

提示

输入

输出

样例输入

样例输出

解题思路

代码实现

结点类

自定义栈

push函数

pop函数

Symbol_matching函数

完整代码

问题二：简单计算器的实现

表达式知识

中缀表达式

后缀表达式

前缀表达式

中缀表达式转后缀表达式

简单计算器题目描述

描述

输入

输出

样例输入

样例输出

解题思路

代码实现

evaluate函数

precedence函数

evaluateExpression函数

完整代码

附录

分类专栏

本专栏上一节

栈

基本概念

栈的定义

栈（Stack）：是只允许在一端进行插入或删除的线性表。首先栈是一种线性表，但限定这种线性表只能在某一端进行插入和删除操作。

在这里插入图片描述


栈顶（Top）：线性表允许进行插入删除的那一端。
栈底（Bottom）：固定的，不允许进行插入和删除的另一端。
空栈：不含任何元素的空表。

栈的特点

栈被称为后进先出（Last In First Out）的线性表，简称LIFO结构，最后压入栈的元素会被最先弹出

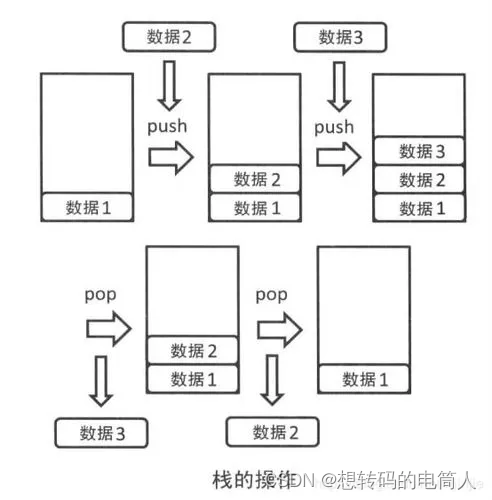
栈的常见基本操作

  1. push：将一个元素压入栈顶。
  2. pop：从栈顶弹出一个元素，并返回它。
  3. top：查看栈顶元素，但不移除它。
  4. isEmpty：检查栈是否为空。
  5. size：获取栈中元素的数量。
  6. clear：清空栈，移除所有元素

了解了栈的功能后，让我们自己实现一个栈，完成下面栈的应用：平衡括号，以及实现一个简单计算器 

栈的应用

问题一：平衡符号

题目描述

在实际编程中，我们经常会嵌套使用括号，如“{}”、“[]”、“()”，如果括号太多，可能会出现括号不匹配的情况，比如“(as))”、“{(bcd})”等。现希望你们编写一个程序，判断输入的一段语句中的括号是否匹配。

注：必须使用栈来实现这一功能，栈类用链表或者数组实现。

提示

可定义一个字典dir，用于字符匹配。map是STL的一个关联容器，它提供一对一的hash。第一个可以称为关键字(key)，每个关键字只能在map中出现一次；第二个以称为该关键字的值(value)。

输入

输入字符串s，s是由{},[],()以及数字、字母组成的字符串(全都是半角字符)。

输出

若括号使用规范且匹配，输出“1”，否则输出“0”。

样例输入

4Print(abc[0]+’This is a {}’)

样例输出

1

解题思路

  1. 遍历输入字符串：我们从头到尾遍历输入的字符串，每次取出一个字符进行处理

  2. 使用栈来跟踪括号的匹配情况：我们使用栈来存储遇到的左括号，每当遇到一个右括号时，就检查栈顶的左括号是否与之匹配。如果匹配，则继续处理，如果不匹配，则括号不匹配

  3. 处理括号：当我们遇到左括号时，将其压入栈中；当遇到右括号时，检查栈顶的左括号是否与之匹配。如果匹配，则继续处理下一个字符；如果不匹配，则括号不匹配

  4. 检查栈的状态：最后，检查栈是否为空。如果为空，则表示所有左括号都有相应的右括号与之匹配，返回True；如果栈不为空，则表示某些左括号没有相应的右括号与之匹配，返回False

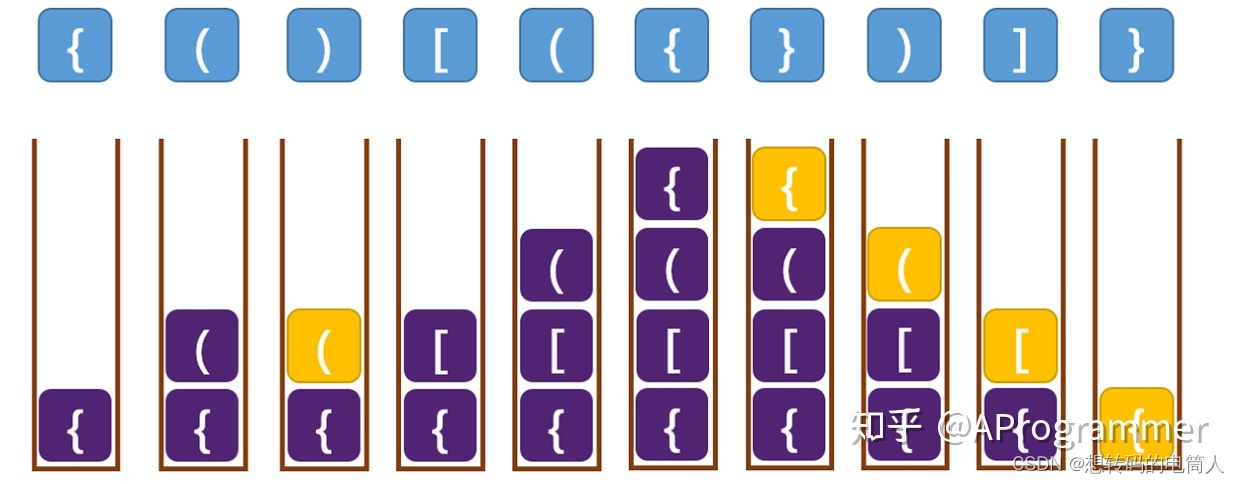
如上图，先将左括号“{”和“(”入栈，当遇到“)”时，弹出栈顶元素“(”，再依次入栈“[”、“(”、“{”，遇到“}”，“)”，“]”，“}”依次弹出栈顶元素进行匹配，最后判断出栈为空，则该括号匹配

代码实现

结点类

结点类包含数据以及next指针，指向下一个结点

  1. struct Node
  2.     {
  3.         char data;
  4.         Node* next;
  5.     };
自定义栈

栈只需要一个栈顶指针head以及size用来记录栈的大小，初始化时将栈顶指针指向空指针，size置为0，析构函数中则清空栈中所有的元素，回收栈空间

  1. class Mystack {
  2. private:
  3.     struct Node
  4.     {
  5.         char data;
  6.         Node* next;
  7.     };
  8.  
  9. public:
  10.     Node* head; // 栈顶指针
  11.     int size;   // 栈大小
  12.  
  13.     Mystack()
  14.     {
  15.         head = nullptr;
  16.         size = 0;
  17.     }; // 初始化空间
  18.  
  19.     ~Mystack()
  20.     {
  21.         Node* q = new Node;
  22.         while (head != nullptr)
  23.         {
  24.             q = head;
  25.             head = head->next;
  26.             delete q;
  27.         }
  28.     } // 回收栈空间
  29. }
push函数

入栈操作，将一个元素压入栈顶，新节点的next指向原栈顶节点，然后更新栈顶指针head，栈的大小size+1

  1. void push(char elem) {
  2.         Node* tmp = new Node();
  3.         tmp->data = elem;
  4.         size = size + 1;
  5.         tmp->next = head;
  6.         head = tmp;
  7.     };
pop函数

出栈操作，删除栈顶节点，释放其内存，更新栈顶指针head，栈大小size-1

  1. void pop() {
  2.         if (head == nullptr) {
  3.             return;
  4.         }
  5.         Node* tmp = head;
  6.         head = head->next;
  7.         delete tmp;
  8.         size = size - 1;
  9.     };
Symbol_matching函数

Symbol_matching函数用于判断输入的字符串中的括号是否匹配

首先定义一个映射表map<char, char> dic，用于存储括号的匹配关系，左括号作为键，右括号作为值，然后遍历字符串的每个字符，如果当前字符是左括号，将其入栈，如果当前字符是右括号，则需进行匹配。每次匹配时，检查栈是否为空，或者栈顶左括号与当前右括号是否匹配，如果不匹配，则返回 false。 如果匹配，则将栈顶左括号出栈。 最后，判断栈是否为空，如果栈为空则表示所有左括号都有相应的右括号与之匹配，返回 true；否则返回 false

  1. bool Symbol_matching(string str) {
  2.     Mystack stack;
  3.     map<char, char> dic = { {'{','}'}, {'[',']'}, {'(',')'} };
  4.     for (char c : str) 
  5.     {
  6.         if (dic.count(c))
  7.         {
  8.             stack.push(c);
  9.         }
  10.         else if (c == '}' || c == ']' || c == ')') 
  11.         {
  12.             if (stack.size == 0 || dic[stack.head->data] != c) {
  13.                 return false;
  14.             }
  15.             else {
  16.                 stack.pop();
  17.             }
  18.         }
  19.     }
  20.     return stack.size == 0;
  21. }

完整代码

  1. #include <iostream>
  2. #include <string>
  3. #include <map>
  4. using namespace std;
  5.  
  6. class Mystack {
  7. private:
  8. 	struct Node
  9. 	{
  10. 		char data;
  11. 		Node* next;
  12. 	};
  13.  
  14. public:
  15. 	Node* head; //栈顶指针 
  16. 	int size; //栈大小
  17.  
  18. 	Mystack()
  19. 	{
  20. 		head = nullptr;
  21. 		size = 0;
  22. 	}; //初始化空间
  23.  
  24. 	~Mystack()
  25. 	{
  26. 		Node* q = new Node;
  27. 		while (head != nullptr)
  28. 		{
  29. 			q = head;
  30. 			head = head->next;
  31. 			delete q;
  32. 		}
  33. 	} //回收栈空间
  34.  
  35. 	void push(char elem) {
  36. 		//请完成入栈函数代码
  37. 		Node* tmp = new Node();
  38. 		tmp->data = elem;
  39. 		size = size + 1;
  40. 		tmp->next = head;
  41. 		head = tmp;
  42. 	};
  43.  
  44. 	void pop() {
  45. 		if (head == nullptr) {
  46. 			return;
  47. 		}
  48. 		//请完成出栈函数代码
  49. 		Node* tmp =head;
  50. 		head = head->next;
  51. 		delete tmp;
  52. 		size = size - 1;
  53. 	};
  54.  
  55. };
  56. bool Symbol_matching(string str) {
  57. 	Mystack stack;
  58. 	map<char, char> dic = { {'{','}'}, {'[',']'}, {'(',')'} };
  59. 	for (char c : str) 
  60. 	{
  61. 		if (dic.count(c))
  62. 		{
  63. 			stack.push(c);
  64. 		}
  65. 		else if (c == '}' || c == ']' || c == ')') 
  66. 		{
  67. 			if (stack.size == 0 || dic[stack.head->data] != c) {
  68. 				return false;
  69. 			}
  70. 			else {
  71. 				stack.pop();
  72. 			}
  73. 		}
  74. 	}
  75. 	return stack.size == 0;
  76. }
  77.  
  78. int main() {
  79. 	string str;
  80. 	bool R;
  81. 	getline(cin, str);
  82. 	R = Symbol_matching(str);
  83. 	cout << R << endl;
  84. 	return 0;
  85. }

问题二：简单计算器的实现

在了解问题二的内容之前，我们先来学习一下三种表达式

表达式知识

中缀表达式

        操作符以中缀形式位于运算数中间（如：3+2），是我们日常通用的算术和逻辑公式表示方法。

后缀表达式

        又称逆波兰式（Reverse Polish Notation - RPN），操作符以后缀形式位于两个运算数后（如：3+2的后缀表达形式就是3 2 +）。

前缀表达式

        又称波兰式（Polish Notation），操作符以前缀形式位于两个运算数前（如：3+2的前缀表达形式就是+ 3 2）

中缀表达式转后缀表达式

参考链接：《数据结构》：中缀表达式转后缀表达式 + 后缀表达式的计算-CSDN博客

从左至右依次遍历中缀表达式各个字符（需要准备一个字符栈存储操作符和括号）

1、字符为运算数 ：

直接送入后缀表达式（注：需要先分析出完整的运算数）。

2、字符为左括号 ：

直接入栈（注：左括号入栈后优先级降至最低）。

3、字符为右括号 ：

直接出栈，并将出栈字符依次送入后缀表达式，直到栈顶字符为左括号（左括号也要出栈，但不送入后缀表达式）。

总结：只要满足 栈顶为左括号 即可进行最后一次出栈。

4、字符为操作符 ：

若栈空，直接入栈。

若栈非空，判断栈顶操作符，若栈顶操作符优先级低于该操作符，该操作符入栈；否则一直出栈，并将出栈字符依次送入后缀表达式，直到栈空或栈顶操作符优先级低于该操作符，该操作符再入栈。

总结：只要满足 栈空 或者 优先级高于栈顶操作符 即可停止出栈，并将该操作符入栈。

5、重复以上步骤直至遍历完成中缀表达式，接着判断字符栈是否为空，非空则直接出栈，并将出栈字符依次送入后缀表达式。

注：中缀表达式遍历完成，栈中可能还有字符未输出，故需要判断栈空。

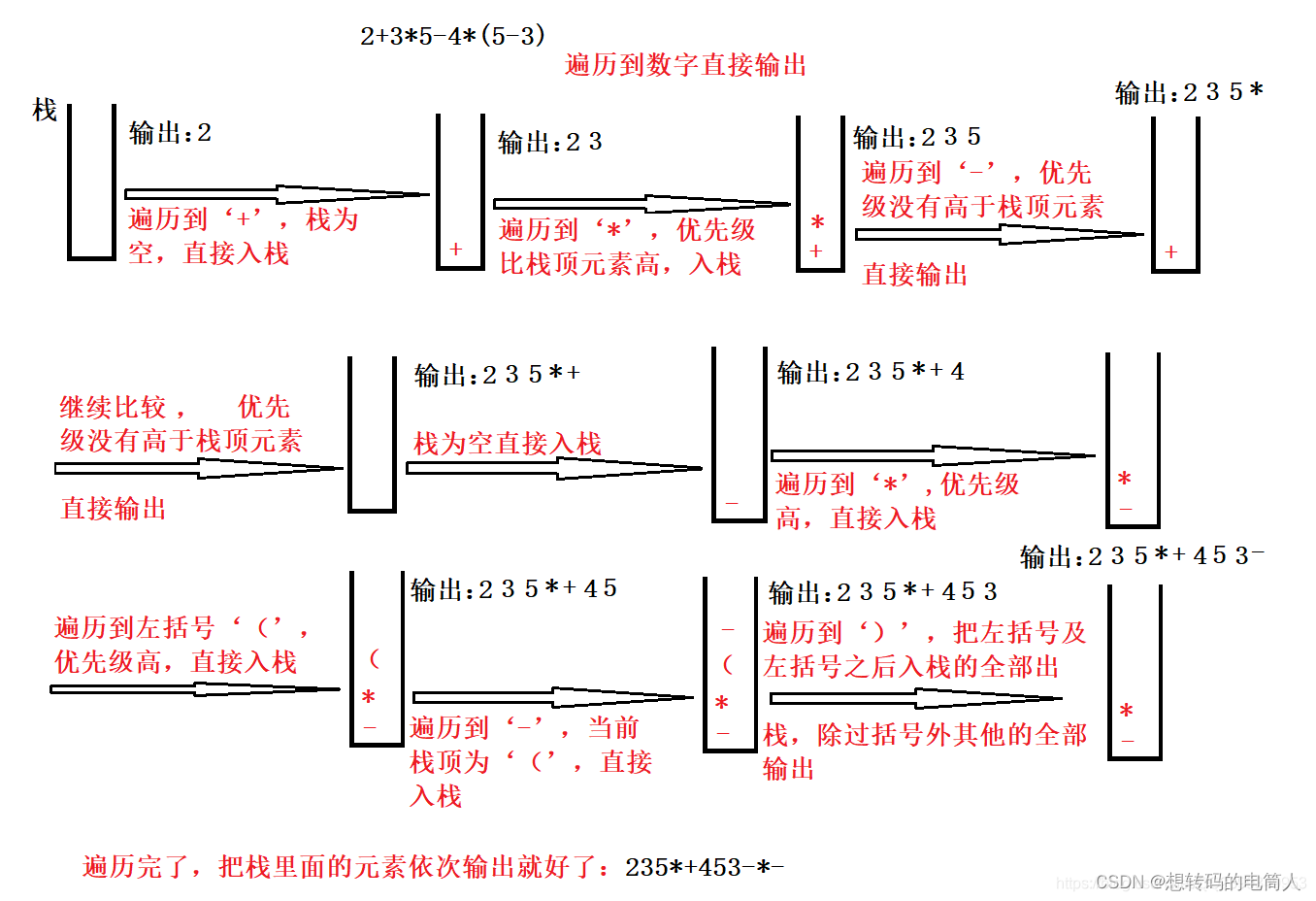
简单计算器题目描述

描述

编写程序，输入一个中缀表达式，最长可容纳80个字符。计算的对象为数据类型为int的正整数，能计算加、减、乘、除，允许使用括号改变优先级。

输入

输入一个中缀表达式。（字符串形式，全都是半角符号）

输出

输出中缀表达式的计算结果

样例输入

(2+3)+(2/3)+(2-3)+(2*3)

样例输出

10

解题思路

首先我们需要使用两个栈，一个存放操作数operands，一个存放运算符operators

然后遍历中缀表达式字符串读取每个字符，并结合栈来处理运算符和操作数。

1、如果是数字，则将其转换为整数，并将其压入操作数栈中。

2、如果是左括号 (，则将其压入运算符栈中。 如果是右括号 )，则执行栈内运算直到遇到匹配的左括号 (，并将结果压入操作数栈中。

3、如果是运算符 + - * /，则根据运算符的优先级决定是否进行运算，并将结果压入操作数栈中。

在遍历完所有字符后，如果运算符栈中还有运算符，则依次执行栈内运算，直到栈为空为止。

最后返回操作数栈中的唯一元素，即为中缀表达式的值

代码实现

这里我们#include<stack>，引入stack库，故不需要重新定义结点类以及栈

evaluate函数

我们定义int evaluate(int left, int right, char op) ，用来得到两个数和对应操作符的计算结果并返回

  1. int evaluate(int left, int right, char op) {
  2.     switch (op) {
  3.         case '+':
  4.             return left + right;
  5.         case '-':
  6.             return left - right;
  7.         case '*':
  8.             return left * right;
  9.         case '/':
  10.             return left / right;
  11.         default:
  12.             return 0;
  13.     }
  14. }
precedence函数

然后我们需要定义precedence(char op)，用来判断运算符的优先级，若为乘除则返回2（即优先级最高），若为加减则返回1

  1. int precedence(char op) {
  2.     if (op == '*' || op == '/') {
  3.         return 2;
  4.     } else if (op == '+' || op == '-') {
  5.         return 1;
  6.     } else {
  7.         return 0;
  8.     }
  9. }
evaluateExpression函数

准备工作完成后，我们需要自定义evaluateExpression函数用来计算中缀表达式

在函数开始时，创建两个栈，一个用于存放操作数 operands，另一个用于存放运算符 operators

遍历输入的中缀表达式expr中的每个字符。每次处理表达式中的一个字符

1、处理操作数： 如果当前字符是数字，表示操作数，则将其转换为整数并压入操作数栈 operands 中。 如果当前字符是一个多位数，则继续读取后续字符直到遇到非数字字符，将其合并成一个完整的操作数。

2、处理左括号： 如果当前字符是左括号"("，则将其压入运算符栈 operators 中。

3、处理右括号： 如果当前字符是右括号")"，则执行栈内运算直到遇到匹配的左括号 (，具体操作是：弹出运算符栈顶的运算符，直到遇到左括号"("。每次弹出运算符时，同时从操作数栈中弹出两个操作数，将它们和运算符进行计算，结果压入操作数栈中。 弹出左括号"("，但不输出到结果。

4、处理运算符： 如果当前字符是运算符 + - * /，则根据其优先级和栈顶运算符的优先级进行比较：如果运算符栈为空，或者当前运算符优先级高于栈顶运算符优先级，则将当前运算符压入运算符栈中。 否则，不断地弹出运算符栈顶运算符直到满足上述条件，并将其压入操作数栈中。

在遍历完所有字符后，如果运算符栈中还有运算符，则依次执行栈内运算，直到栈为空为止

最后返回操作数栈顶的元素，即为中缀表达式的值。

  1. int evaluateExpression(const string& expr) {
  2.     stack<int> operands;
  3.     stack<char> operators;
  4.  
  5.     for (int i = 0; i < expr.length(); i++) {
  6.         char c = expr[i];
  7.  
  8.         if (isdigit(c)) {
  9.             int num = c - '0';
  10.             while (i + 1 < expr.length() && isdigit(expr[i + 1])) {
  11.                 num = num * 10 + (expr[i + 1] - '0');
  12.                 i++;
  13.             }
  14.             operands.push(num);
  15.         } else if (c == '(') {
  16.             operators.push(c);
  17.         } else if (c == ')') {
  18.             while (!operators.empty() && operators.top() != '(') {
  19.                 char op = operators.top();
  20.                 operators.pop();
  21.                 int right = operands.top();
  22.                 operands.pop();
  23.                 int left = operands.top();
  24.                 operands.pop();
  25.                 operands.push(evaluate(left, right, op));
  26.             }
  27.             operators.pop();
  28.         } else if (c == '+' || c == '-' || c == '*' || c == '/') {
  29.             while (!operators.empty() && precedence(operators.top()) >= precedence(c)) {
  30.                 char op = operators.top();
  31.                 operators.pop();
  32.                 int right = operands.top();
  33.                 operands.pop();
  34.                 int left = operands.top();
  35.                 operands.pop();
  36.                 operands.push(evaluate(left, right, op));
  37.             }
  38.             operators.push(c);
  39.         }
  40.     }
  41.     while (!operators.empty()) {
  42.     char op = operators.top();
  43.     operators.pop();
  44.     int right = operands.top();
  45.     operands.pop();
  46.     int left = operands.top();
  47.     operands.pop();
  48.     operands.push(evaluate(left, right, op));
  49. }
  50.  
  51. return operands.top();
  52. }

完整代码

  1. #include <iostream>
  2. #include <stack>
  3. #include <string>
  4. #include <cctype>
  5.  
  6. using namespace std;
  7.  
  8. int precedence(char op) {
  9.     if (op == '*' || op == '/') {
  10.         return 2;
  11.     } else if (op == '+' || op == '-') {
  12.         return 1;
  13.     } else {
  14.         return 0;
  15.     }
  16. }
  17.  
  18. int evaluate(int left, int right, char op) {
  19.     switch (op) {
  20.         case '+':
  21.             return left + right;
  22.         case '-':
  23.             return left - right;
  24.         case '*':
  25.             return left * right;
  26.         case '/':
  27.             return left / right;
  28.         default:
  29.             return 0;
  30.     }
  31. }
  32.  
  33. int evaluateExpression(const string& expr) {
  34.     stack<int> operands;
  35.     stack<char> operators;
  36.  
  37.     for (int i = 0; i < expr.length(); i++) {
  38.         char c = expr[i];
  39.  
  40.         if (isdigit(c)) {
  41.             int num = c - '0';
  42.             while (i + 1 < expr.length() && isdigit(expr[i + 1])) {
  43.                 num = num * 10 + (expr[i + 1] - '0');
  44.                 i++;
  45.             }
  46.             operands.push(num);
  47.         } else if (c == '(') {
  48.             operators.push(c);
  49.         } else if (c == ')') {
  50.             while (!operators.empty() && operators.top() != '(') {
  51.                 char op = operators.top();
  52.                 operators.pop();
  53.                 int right = operands.top();
  54.                 operands.pop();
  55.                 int left = operands.top();
  56.                 operands.pop();
  57.                 operands.push(evaluate(left, right, op));
  58.             }
  59.             operators.pop();
  60.         } else if (c == '+' || c == '-' || c == '*' || c == '/') {
  61.             while (!operators.empty() && precedence(operators.top()) >= precedence(c)) {
  62.                 char op = operators.top();
  63.                 operators.pop();
  64.                 int right = operands.top();
  65.                 operands.pop();
  66.                 int left = operands.top();
  67.                 operands.pop();
  68.                 operands.push(evaluate(left, right, op));
  69.             }
  70.             operators.push(c);
  71.         }
  72.     }
  73.     while (!operators.empty()) {
  74.     char op = operators.top();
  75.     operators.pop();
  76.     int right = operands.top();
  77.     operands.pop();
  78.     int left = operands.top();
  79.     operands.pop();
  80.     operands.push(evaluate(left, right, op));
  81. }
  82.  
  83. return operands.top();
  84. }
  85.  
  86. int main() {
  87. string expr;
  88. getline(cin, expr);
  89.  
  90. int result = evaluateExpression(expr);
  91. cout << result << endl;
  92.  
  93. return 0;
  94. }

附录

分类专栏

链接：

​​​​​手把手教数据结构与算法

本专栏上一节

链接：

手把手教数据结构与算法：循环单链表设计（约瑟夫问题）-CSDN博客

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/Gausst松鼠会/article/detail/728797
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号