devbox
IT小白
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

【解决（几乎）任何机器学习问题】：超参数优化篇（超详细）

作者：IT小白 | 2024-02-19 21:05:05

赞

踩

【解决（几乎）任何机器学习问题】：超参数优化篇（超详细）
这篇文章相当长，您可以添加至收藏夹，以便在后续有空时候悠闲地阅读。
有了优秀的模型，就有了优化超参数以获得最佳得分模型的难题。那么，什么是超参数优化呢？假设您的机器学习项⽬有⼀个简单的流程。有⼀个数据集，你直接应⽤⼀个模型，然后得到结 果。模型在这⾥的参数被称为超参数，即控制模型训练/拟合过程的参数。如果我们⽤ SGD 训练线性回归，模型的参数是斜率和偏差，超参数是学习率。你会发现我在本章和本书中交替使⽤这些术语。假设模型中有三个参数 a、b、c，所有这些参数都可以是 1 到 10 之间的整数。这些参数 的 "正确 "组合将为您提供最佳结果。因此，这就有点像⼀个装有三拨密码锁的⼿提箱。不过，三拨密码锁只有⼀个正确答案。⽽模型有很多正确答案。那么，如何找到最佳参数呢？⼀种⽅法是对所有组合进⾏评估，看哪种组合能提⾼指标。让我们看看如何做到这⼀点。 
  1. best_accuracy = 0
  2. best_parameters = {"a": 0, "b": 0, "c": 0}
  3. for a in range(1, 11):
  4.     for b in range(1, 11):
  5.         for c in range(1, 11):
  6.             model = MODEL(a, b, c)
  7.             model.fit(training_data)
  8.             preds = model.predict(validation_data)
  9.             accuracy = metrics.accuracy_score(targets, preds)
  10.             if accuracy > best_accuracy:
  11.                 best_accuracy = accuracy
  12.                 best_parameters["a"] = a
  13.                 best_parameters["b"] = b
  14.                 best_parameters["c"] = c
在上述代码中，我们从 1 到 10 对所有参数进⾏了拟合。因此，我们总共要对模型进⾏ 1000 次（10 x 10 x 10）拟合。这可能会很昂贵，因为模型的训练需要很⻓时间。不过，在这种情况下应 该没问题，但在现实世界中，并不是只有三个参数，每个参数也不是只有⼗个值。 ⼤多数模型参 数都是实数，不同参数的组合可以是⽆限的。
让我们看看 scikit-learn 的随机森林模型。 
  1. RandomForestClassifier(
  2.     n_estimators=100,
  3.     criterion='gini',
  4.     max_depth=None,
  5.     min_samples_split=2,
  6.     min_samples_leaf=1,
  7.     min_weight_fraction_leaf=0.0,
  8.     max_features='auto',
  9.     max_leaf_nodes=None,
  10.     min_impurity_decrease=0.0,
  11.     min_impurity_split=None,
  12.     bootstrap=True,
  13.     oob_score=False,
  14.     n_jobs=None,
  15.     random_state=None,
  16.     verbose=0,
  17.     warm_start=False,
  18.     class_weight=None,
  19.     ccp_alpha=0.0,
  20.     max_samples=None,
  21.     )
有 19 个参数，⽽所有这些参数的所有组合，以及它们可以承担的所有值，都将是⽆穷⽆尽的。通常情况下，我们没有⾜够的资源和时间来做这件事。因此，我们指定了⼀个参数⽹格。在这个⽹格上寻找最佳参数组合的搜索称为⽹格搜索。我们可以说，n_estimators 可以是 100、200、250、300、400、500；max_depth 可以是 1、2、5、7、11、15；criterion 可以是 gini 或 entropy。这些参数看起来并不多，但如果数据集过⼤，计算起来会耗费⼤量时间。我们可以像之前⼀样创建三个 for 循环，并在验证集上计算得分，这样就能实现⽹格搜索。还必须注意的是，如果要进⾏ k 折交叉验证，则需要更多的循环，这意味着需要更多的时间来找到完美的参数。因此，⽹格搜索并不流⾏。让我们以根据 ⼿机配置预测⼿机价格范围 数据集为例，看看它是如何实现的。

 

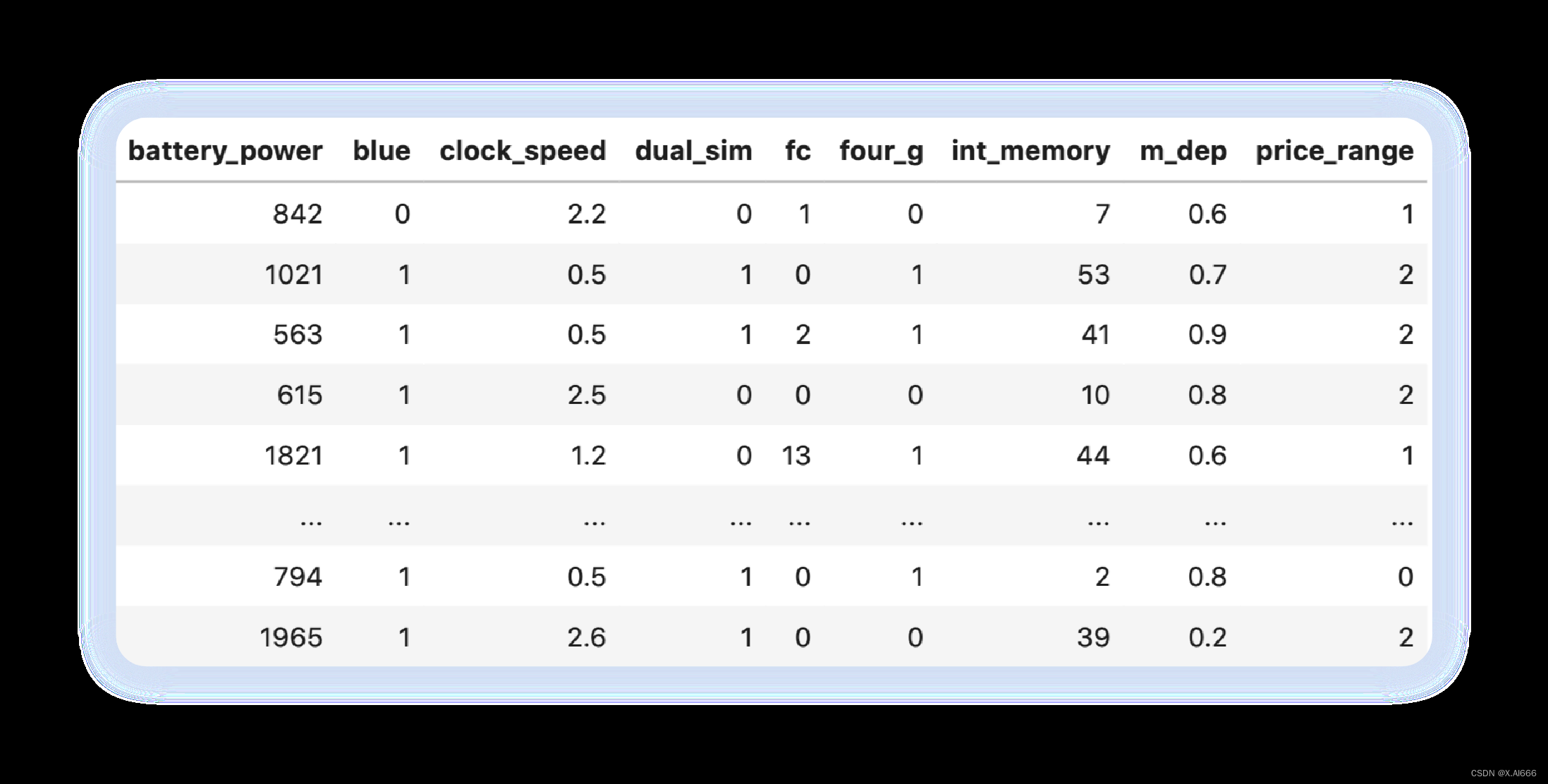
图 1 ：⼿机配置预测⼿机价格范围数据集展⽰
训练集中只有 2000 个样本。我们可以轻松地使⽤分层 kfold 和准确率作为评估指标。我们将使⽤ 具有上述参数范围的随机森林模型，并在下⾯的⽰例中了解如何进⾏⽹格搜索。 
  1. # rf_grid_search.py
  2. import numpy as np
  3. import pandas as pd
  4. from sklearn import ensemble
  5. from sklearn import metrics
  6. from sklearn import model_selection
  7.  
  8. if __name__ == "__main__":
  9.     df = pd.read_csv("./input/mobile_train.csv")
  10.     X = df.drop("price_range", axis=1).values
  11.     y = df.price_range.values
  12.  
  13.     classifier = ensemble.RandomForestClassifier(n_jobs=-1)
  14.     param_grid = {
  15.         "n_estimators": [100, 200, 250, 300, 400, 500],
  16.         "max_depth": [1, 2, 5, 7, 11, 15],
  17.         "criterion": ["gini", "entropy"]
  18.     }
  19.  
  20.     model = model_selection.GridSearchCV(
  21.         estimator=classifier,
  22.         param_grid=param_grid,
  23.         scoring="accuracy",
  24.         verbose=10,
  25.         n_jobs=1,
  26.         cv=5
  27.     )
  28.  
  29.     model.fit(X, y)
  30.     print(f"Best score: {model.best_score_}")
  31.     print("Best parameters set:")
  32.     best_parameters = model.best_estimator_.get_params()
  33.     for param_name in sorted(param_grid.keys()):
  34.         print(f"\t{param_name}: {best_parameters[param_name]}")
这⾥打印了很多内容，让我们看看最后⼏⾏。
[ CV ] criterion = entropy , max_depth = 15 , n_estimators = 500 , score = 0.895 ,
total = 1.0 s
[ CV ] criterion = entropy , max_depth = 15 , n_estimators = 500 ...............
[ CV ] criterion = entropy , max_depth = 15 , n_estimators = 500 , score = 0.890 ,
total = 1.1 s
[ CV ] criterion = entropy , max_depth = 15 , n_estimators = 500 ...............
[ CV ] criterion = entropy , max_depth = 15 , n_estimators = 500 , score = 0.910 ,
total = 1.1 s
[ CV ] criterion = entropy , max_depth = 15 , n_estimators = 500 ...............
[ CV ] criterion = entropy , max_depth = 15 , n_estimators = 500 , score = 0.880 ,
total = 1.1 s
[ CV ] criterion = entropy , max_depth = 15 , n_estimators = 500 ...............
[ CV ] criterion = entropy , max_depth = 15 , n_estimators = 500 , score = 0.870 , total = 1.1 s
[ Parallel ( n_jobs = 1 )]: Done 360 out of 360 | elapsed : 3.7 min finished
Best score : 0.889
Best parameters set :
criterion : 'entropy'
max_depth : 15
n_estimators : 500
最后，我们可以看到，5折交叉检验最佳得分是 0.889，我们的⽹格搜索得到了最佳参数。我们可 以使⽤的下⼀个最佳⽅法是 随机搜索 。在随机搜索中，我们随机选择⼀个参数组合，然后计算交 叉验证得分。这⾥消耗的时间⽐⽹格搜索少，因为我们不对所有不同的参数组合进⾏评估。我们 选择要对模型进⾏多少次评估，这就决定了搜索所需的时间。代码与上⾯的差别不⼤。除了GridSearchCV 外，我们使⽤ RandomizedSearchCV。 
  1. if __name__ == "__main__":
  2.     classifier = ensemble.RandomForestClassifier(n_jobs=-1)
  3.     param_grid = {
  4.         "n_estimators": np.arange(100, 1500, 100),
  5.         "max_depth": np.arange(1, 31),
  6.         "criterion": ["gini", "entropy"]
  7.     }
  8.     model = model_selection.RandomizedSearchCV(
  9.         estimator=classifier,
  10.         param_distributions=param_grid,
  11.         n_iter=20,
  12.         scoring="accuracy",
  13.         verbose=10,
  14.         n_jobs=1,
  15.         cv=5
  16.     )
  17.     model.fit(X, y)
  18.     print(f"Best score: {model.best_score_}")
  19.     print("Best parameters set:")
  20.     best_parameters = model.best_estimator_.get_params()
  21.     for param_name in sorted(param_grid.keys()):
  22.         print(f"\t{param_name}: {best_parameters[param_name]}")

我们更改了随机搜索的参数⽹格，结果似乎有了些许改进。

Best score : 0.8905
Best parameters set :
criterion : entropy
max_depth : 25
n_estimators : 300
如果迭代次数较少，随机搜索⽐⽹格搜索更快。使⽤这两种⽅法，你可以为各种模型找到最优参 数，只要它们有拟合和预测功能，这也是 scikit-learn 的标准。有时，你可能想使⽤管道。例如假设我们正在处理⼀个多类分类问题。在这个问题中，训练数据由两列⽂本组成，你需要建⽴⼀个模型来预测类别。让我们假设你选择的管道是⾸先以半监督的⽅式应⽤ tf-idf，然后使⽤SVD 和SVM 分类器。现在的问题是，我们必须选择 SVD 的成分，还需要调整 SVM 的参数。下⾯的代段展⽰了如何做到这⼀点。 

  1. import numpy as np
  2. import pandas as pd
  3. from sklearn import metrics
  4. from sklearn import model_selection
  5. from sklearn import pipeline
  6. from sklearn.decomposition import TruncatedSVD
  7. from sklearn.feature_extraction.text import TfidfVectorizer
  8. from sklearn.preprocessing import StandardScaler
  9. from sklearn.svm import SVC
  10.  
  11. def quadratic_weighted_kappa(y_true, y_pred):
  12.     return metrics.cohen_kappa_score(y_true, y_pred, weights="quadratic")
  13.  
  14. if __name__ == '__main__':
  15.     train = pd.read_csv('./input/train.csv')
  16.     idx = test.id.values.astype(int)
  17.     train = train.drop('id', axis=1)
  18.     test = test.drop('id', axis=1)
  19.  
  20.     y = train.relevance.values
  21.     traindata = list(train.apply(lambda x:'%s %s' % (x['text1'], x['text2']), axis=1))
  22.     testdata = list(test.apply(lambda x:'%s %s' % (x['text1'], x['text2']), axis=1))
  23.  
  24.     tfv = TfidfVectorizer(
  25.         min_df=3,
  26.         max_features=None,
  27.         strip_accents='unicode',
  28.         analyzer='word',
  29.         token_pattern=r'\w{1,}',
  30.         ngram_range=(1, 3),
  31.         use_idf=1,
  32.         smooth_idf=1,
  33.         sublinear_tf=1,
  34.         stop_words='english'
  35.     )
  36.  
  37.     tfv.fit(traindata)
  38.     X = tfv.transform(traindata)
  39.     X_test = tfv.transform(testdata)
  40.  
  41.     svd = TruncatedSVD()
  42.     scl = StandardScaler()
  43.     svm_model = SVC()
  44.  
  45.     clf = pipeline.Pipeline([
  46.         ('svd', svd),
  47.         ('scl', scl),
  48.         ('svm', svm_model)
  49.     ])
  50.  
  51.     param_grid = {
  52.         'svd__n_components': [200, 300],
  53.         'svm__C': [10, 12]
  54.     }
  55.  
  56.     kappa_scorer = metrics.make_scorer(
  57.         quadratic_weighted_kappa,
  58.         greater_is_better=True
  59.     )
  60.  
  61.     model = model_selection.GridSearchCV(
  62.         estimator=clf,
  63.         param_grid=param_grid,
  64.         scoring=kappa_scorer,
  65.         verbose=10,
  66.         n_jobs=-1,
  67.         refit=True,
  68.         cv=5
  69.     )
  70.  
  71.     model.fit(X, y)
  72.     print("Best score: %0.3f" % model.best_score_)
  73.     print("Best parameters set:")
  74.     best_parameters = model.best_estimator_.get_params()
  75.     for param_name in sorted(param_grid.keys()):
  76.         print("\t%s: %r" % (param_name, best_parameters[param_name]))
  77.  
  78.     best_model = model.best_estimator_
  79.     best_model.fit(X, y)
  80.     preds = best_model.predict(X_test)
这⾥显⽰的管道包括 SVD（奇异值分解）、标准缩放和 SVM（⽀持向量机）模型。请注意，由于没有训练数据，您⽆法按原样运⾏上述代码。当我们进⼊⾼级超参数优化技术时，我们可以使⽤ 不同类型的 最⼩化算法 来研究函数的最⼩化。这可以通过使⽤多种最⼩化函数来实现，如下坡单 纯形算法、内尔德-梅德优化算法、使⽤⻉叶斯技术和⾼斯过程寻找最优参数或使⽤遗传算法。 我将在 "集合与堆叠（ensembling and stacking） "⼀章中详细介绍下坡单纯形算法和 NelderMead 算法的应⽤。⾸先，让我们看看⾼斯过程如何⽤于超参数优化。这类算法需要⼀个可以优化的函数。⼤多数情况下，都是最⼩化这个函数，就像我们最⼩化损失⼀样。因此，⽐⽅说，你想找到最佳参数以获得最佳准确度，显然，准确度越⾼越好。现在，我们不能最⼩化精确度，但我们可以将精确度乘以-1。这样，我们是在最⼩化精确度的负值，但事实上，我们是在最⼤化精确度。 在⾼斯过程中使⽤⻉叶斯优化，可以使⽤ scikit-optimize (skopt) 库中的 gp_minimize 函数。让我们看看如何使⽤该函数调整随机森林模型的参数。 

  1. # rf_gp_minimize.py
  2. import numpy as np
  3. import pandas as pd
  4. from functools import partial
  5. from sklearn import ensemble
  6. from sklearn import metrics
  7. from sklearn import model_selection
  8. from skopt import gp_minimize
  9. from skopt import space
  10.  
  11. def optimize(params, param_names, x, y):
  12.     params = dict(zip(param_names, params))
  13.     model = ensemble.RandomForestClassifier(**params)
  14.     kf = model_selection.StratifiedKFold(n_splits=5)
  15.     accuracies = []
  16.  
  17.     for idx in kf.split(X=x, y=y):
  18.         train_idx, test_idx = idx[0], idx[1]
  19.         xtrain = x[train_idx]
  20.         ytrain = y[train_idx]
  21.         xtest = x[test_idx]
  22.         ytest = y[test_idx]
  23.  
  24.         model.fit(xtrain, ytrain)
  25.         preds = model.predict(xtest)
  26.         fold_accuracy = metrics.accuracy_score(ytest, preds)
  27.         accuracies.append(fold_accuracy)
  28.  
  29.     return -1 * np.mean(accuracies)
  30.  
  31. if __name__ == "__main__":
  32.     df = pd.read_csv("./input/mobile_train.csv")
  33.     X = df.drop("price_range", axis=1).values
  34.     y = df.price_range.values
  35.  
  36.     param_space = [
  37.         space.Integer(3, 15, name="max_depth"),
  38.         space.Integer(100, 1500, name="n_estimators"),
  39.         space.Categorical(["gini", "entropy"], name="criterion"),
  40.         space.Real(0.01, 1, prior="uniform", name="max_features")
  41.     ]
  42.  
  43.     param_names = [
  44.         "max_depth",
  45.         "n_estimators",
  46.         "criterion",
  47.         "max_features"
  48.     ]
  49.  
  50.     optimization_function = partial(
  51.         optimize,
  52.         param_names=param_names,
  53.         x=X,
  54.         y=y
  55.     )
  56.  
  57.     result = gp_minimize(
  58.         optimization_function,
  59.         dimensions=param_space,
  60.         n_calls=15,
  61.         n_random_starts=10,
  62.         verbose=10
  63.     )
  64.  
  65.     best_params = dict(
  66.         zip(
  67.             param_names,
  68.             result.x
  69.         )
  70.     )
  71.     print(best_params)

这同样会产⽣⼤量输出，最后⼀部分如下所⽰。

Iteration No : 14 started . Searching for the next optimal point .
Iteration No : 14 ended . Search finished for the next optimal point .
Time taken : 4.7793
Function value obtained : - 0.9075
Current minimum : - 0.9075
Iteration No : 15 started . Searching for the next optimal point .
Iteration No : 15 ended . Search finished for the next optimal point .
Time taken : 49.4186
Function value obtained : - 0.9075
Current minimum : - 0.9075
{ 'max_depth' : 12 , 'n_estimators' : 100 , 'criterion' : 'entropy' ,
'max_features' : 1.0 }
看来我们已经成功突破了 0.90的准确率。这真是太神奇了！
我们还可以通过以下代码段查看（绘制）我们是如何实现收敛的。
from skopt . plots import plot_convergence
plot_convergence ( result )

收敛图如图 2 所⽰。

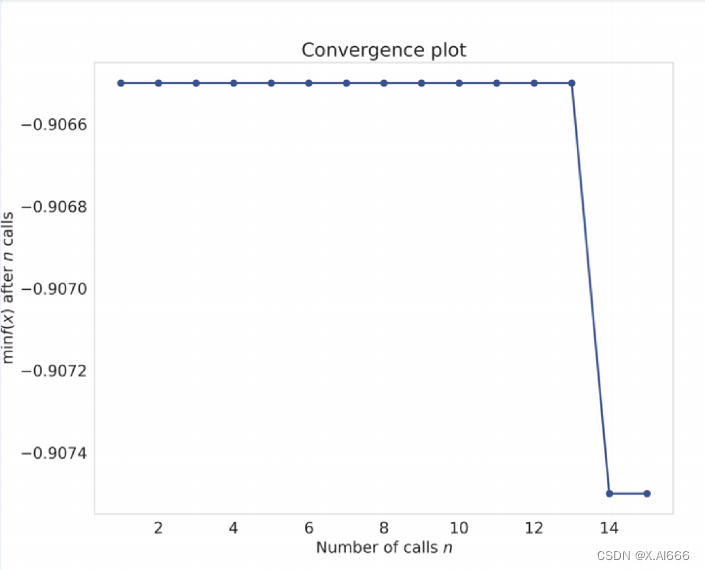
图 2：随机森林参数优化的收敛图
Scikit- optimize 就是这样⼀个库。 hyperopt 使⽤树状结构帕岑估计器（TPE）来找到最优参数。请看下⾯的代码⽚段，我在使⽤ hyperopt 时对之前的代码做了最⼩的改动。 

  1. import numpy as np
  2. import pandas as pd
  3. from functools import partial
  4. from sklearn import ensemble
  5. from sklearn import metrics
  6. from sklearn import model_selection
  7. from hyperopt import hp, fmin, tpe, Trials
  8. from hyperopt.pyll.base import scope
  9.  
  10. def optimize(params, x, y):
  11.     model = ensemble.RandomForestClassifier(**params)
  12.     kf = model_selection.StratifiedKFold(n_splits=5)
  13.     accuracies = []
  14.  
  15.     for idx in kf.split(X=x, y=y):
  16.         train_idx, test_idx = idx[0], idx[1]
  17.         xtrain = x[train_idx]
  18.         ytrain = y[train_idx]
  19.         xtest = x[test_idx]
  20.         ytest = y[test_idx]
  21.  
  22.         model.fit(xtrain, ytrain)
  23.         preds = model.predict(xtest)
  24.         fold_accuracy = metrics.accuracy_score(ytest, preds)
  25.         accuracies.append(fold_accuracy)
  26.  
  27.     return -1 * np.mean(accuracies)
  28.  
  29. if __name__ == "__main__":
  30.     df = pd.read_csv("./input/mobile_train.csv")
  31.     X = df.drop("price_range", axis=1).values
  32.     y = df.price_range.values
  33.  
  34.     param_space = {
  35.         "max_depth": scope.int(hp.quniform("max_depth", 1, 15, 1)),
  36.         "n_estimators": scope.int(hp.quniform("n_estimators", 100, 1500, 1)),
  37.         "criterion": hp.choice("criterion", ["gini", "entropy"]),
  38.         "max_features": hp.uniform("max_features", 0, 1)
  39.     }
  40.  
  41.     optimization_function = partial(
  42.         optimize,
  43.         x=X,
  44.         y=y
  45.     )
  46.  
  47.     trials = Trials()
  48.     hopt = fmin(
  49.         fn=optimization_function,
  50.         space=param_space,
  51.         algo=tpe.suggest,
  52.         max_evals=15,
  53.         trials=trials
  54.     )
  55.  
  56.     print(hopt)
正如你所看到的，这与之前的代码并⽆太⼤区别。你必须以不同的格式定义参数空间，还需要改
变实际优化部分，⽤ hyperopt 代替 gp_minimize。结果相当不错！
❯ python rf_hyperopt . py
100 %| ██████████████████ | 15 / 15 [ 0 4 : 38 < 0 0 : 0 0 , 18.57 s / trial , best loss : -
0.9095000000000001 ]
{ 'criterion' : 1 , 'max_depth' : 11.0 , 'max_features' : 0.821163568049807 ,
'n_estimators' : 806.0 }

我们得到了⽐以前更好的准确度和⼀组可以使⽤的参数。请注意，最终结果中的标准是 1。这意味着选择了 1，即熵。 上述调整超参数的⽅法是最常⻅的，⼏乎适⽤于所有模型：线性回归、逻辑回归、基于树的⽅法、梯度提升模型（如 xgboost、lightgbm），甚⾄神经⽹络！
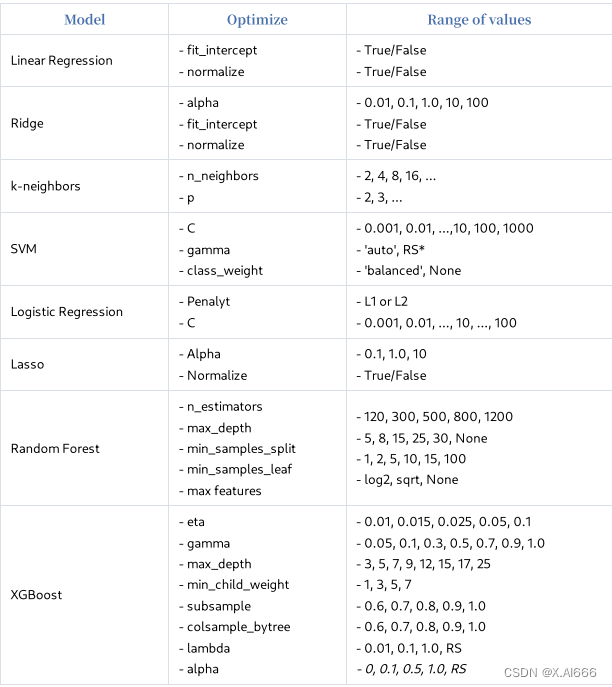
虽然这些⽅法已经存在，但学习时必须从⼿动调整超参数开始，即⼿⼯调整。⼿动调整可以帮助 你学习基础知识，例如，在梯度提升中，当你增加深度时，你应该降低学习率。如果使⽤⾃动⼯ 具，就⽆法学习到这⼀点。请参考下表，了解应如何调整。RS* 表⽰随机搜索应该更好.
⼀旦你能更好地⼿动调整参数，你甚⾄可能不需要任何⾃动超参数调整。创建⼤型模型或引⼊⼤ 量特征时，也容易造成训练数据的过度拟合。为避免过度拟合，需要在训练数据特征中引⼊噪声 或对代价函数进⾏惩罚。这种惩罚称为 正则化 ，有助于泛化模型。在线性模型中，最常⻅的正则 化类型是 L1 和 L2。L1 也称为 Lasso 回归，L2 称为 Ridge 回归。说到神经⽹络，我们会使⽤ dropout、添加增强、噪声等⽅法对模型进⾏正则化。利⽤超参数优化，还可以找到正确的惩罚⽅法。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/IT小白/article/detail/116798?site
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号