devbox
IT小白
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

嵌入式开发学习--数据结构--顺序表、链表、双向链表、顺序栈、链式栈、循环队列、链式队列（含代码）

作者：IT小白 | 2024-04-10 07:15:53

赞

踩

嵌入式开发学习--数据结构--顺序表、链表、双向链表、顺序栈、链式栈、循环队列、链式队列（含代码）

顺序表

特点：内存连续，数组
1）逻辑结构：线性结构
2）存储结构：顺序存储
3）操作：增删改查
函数名命名规则：
下滑线法：create_empty_seqlist
小驼峰法：createEmptySeqList
大驼峰法：CreateEmptySeqList

#ifndef _SEQLIST_H_
#define _SEQLIST_H_

#include<stdio.h>
#include<stdlib.h>
#define N 5
typedef struct 
{
	int data[N];
	int last;//last代表的是数组中最后一个有效元素的下标
}seqlist_t;
//1.创建一个空的顺序表
seqlist_t *CreateEpSeqlist();//返回的是申请空间的首地址
//2.向顺序表的指定位置插入数据
int InsertIntoSeqlist(seqlist_t *p, int post,int data);//post第几个位置，data插入的数据
//3.遍历顺序表sequence 顺序　list 表
void ShowSeqlist(seqlist_t *p);
//4.判断顺序表是否为满,满返回１　未满返回０
int IsFullSeqlist(seqlist_t *p);
//5.判断顺序表是否为空
int IsEpSeqlist(seqlist_t *p);
//6.删除顺序表中指定位置的数据post删除位置
int DeletePostSeqlist(seqlist_t *p, int post);
//7.清空顺序表
void ClearSeqList(seqlist_t *p);
//8.修改指定位置的数据
int ChangePostSeqList(seqlist_t *p,int post,int data);//post被修改的位置，data修改成的数据
//9.查找指定数据出现的位置
int SearchDataSeqList(seqlist_t *p,int data);//data代表被查找的数据
#endif

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30

操作代码

#include "seqlist.h"
//1.创建一个空的顺序表
seqlist_t *CreateEpSeqlist()
{
    //1.动态开辟一个结构体大小的空间
    seqlist_t *p = (seqlist_t *)malloc(sizeof(seqlist_t));
    if (p == NULL)
    {
        perror("malloc err");
    }
    //2.对last初始化
    p->last = -1; //表示当前顺序表为空，无有效元素
    return p;
}
//4.判断顺序表是否为满,满返回１　未满返回０
int IsFullSeqlist(seqlist_t *p)
{
    return p->last + 1 == N;
}
//2.向顺序表的指定位置插入数据
int InsertIntoSeqlist(seqlist_t *p, int post, int data)
{
    //1.容错判断
    if (IsFullSeqlist(p) || post < 0 || post > p->last + 1)
    {
        printf("InsertIntoSeqlist err\n");
        return -1;
    }
    for (int i = p->last; i >= post; i--)
    {
        p->data[i + 1] = p->data[i];
    }
    p->data[post] = data;
    p->last++;
}
//3.遍历顺序表sequence 顺序　list 表
void ShowSeqlist(seqlist_t *p)
{
    for (int i = 0; i <= p->last; i++)
    {
        printf("%d ", p->data[i]);
    }
}
//5.判断顺序表是否为空
int IsEpSeqlist(seqlist_t *p)
{
    return p->last == -1;
}
//6.删除顺序表中指定位置的数据post删除位置
int DeletePostSeqlist(seqlist_t *p, int post)
{
    if (IsEpSeqlist(p) || post < 0 || post > p->last)
    {
        printf("DeletePostSeqlist err\n");
        return -1;
    }
    for (int i = post; i <= p->last; i++)
    {
        p->data[i] = p->data[i + 1];
    }
    p->last--;
    return 0;
}
//7.清空顺序表
void ClearSeqList(seqlist_t *p)
{
    p->last = -1;
}
//8.修改指定位置的数据
int ChangePostSeqList(seqlist_t *p, int post, int data) //post被修改的位置，data修改成的数据
{
    if (post < 0 || post > p->last)
    {
        printf("ChangePostSeqList err\n");
        return -1;
    }
    p->data[post] = data;
    return 0;
}
//9.查找指定数据出现的位置
int SearchDataSeqList(seqlist_t *p, int data) //data代表被查找的数据
{
    if (IsEpSeqlist(p))
    {
        printf("SearchDataSeqList err\n");
        return -1;
    }
    for (int i = 0; i <= p->last; i++)
        if (p->data[i] == data)
            //printf("%d", i);
            return i;
    return -1;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93

顺序表总结:
(1)顺序表在内存当中是连续存储的
(2)顺序表的长度是固定 //#define N 5
(3)顺序表查找数据的时候方便的，插入和删除麻烦

链表

解决了：长度固定，插入删除麻烦的问题
1）逻辑结构：线性结构
2）存储结构：链式存储结构
3）操作：增删改查

单向链表

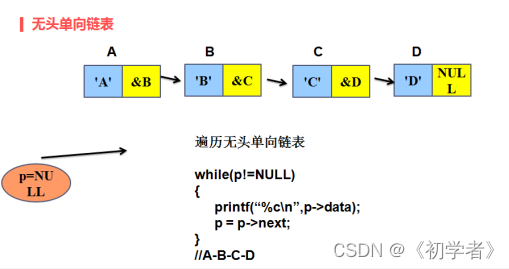
无头单向链表
每个节点的数据域和指针域都有效
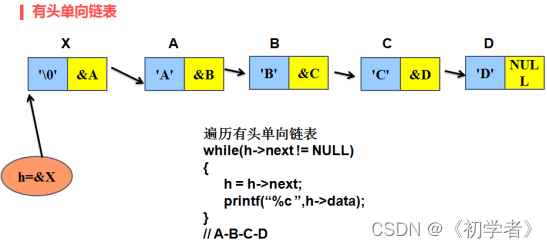
图片来源网络，侵权立删
有头单向链表
存在一个头节点，头节点的数据域无效，但指针域有效
图片来源网络，侵权立删
有头单向链表相关操作

#ifndef _LINKLIST_H_
#define _LINKLIST_H_

typedef int datatype;
typedef struct node_t
{
	datatype data;//数据域
	struct node_t *next;//指针域,指向自身结构体的指针
}link_node_t,*link_list_t;

//1.创建一个空的单向链表(有头单向链表)
link_node_t *CreateEpLinkList();
//2.向单向链表的指定位置插入数据
//p保存链表的头指针 post 插入的位置 data插入的数据
int InsertIntoPostLinkList(link_node_t *p,int post, datatype data);
//3.遍历单向链表
void ShowLinkList(link_node_t *p);
//4.求单向链表长度的函数
int LengthLinkList(link_node_t *p);
//5.删除单向链表中指定位置的数据 post 代表的是删除的位置
int DeletePostLinkList(link_node_t *p, int post);
//6.判断单向链表是否为空 1代表空 0代表非空
int IsEpLinkList(link_node_t *p);
//7.修改指定位置的数据 post 被修改的位置 data修改成的数据
int ChangePostLinkList(link_node_t *p, int post, datatype data);
//8.查找指定数据出现的位置 data被查找的数据 //search 查找
int SearchDataLinkList(link_node_t *p, datatype data);
//9.删除单向链表中出现的指定数据,data代表将单向链表中出现的所有data数据删除
int DeleteDataLinkList(link_node_t *p, datatype data);
//10.转置链表
void ReverseLinkList(link_node_t *p);
//11.清空单向链表
void ClearLinkList(link_node_t *p);
#endif

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34

操作代码

#include "link_list.h"

//1.创建一个空的单向链表(有头单向链表)
link_node_t *CreateEpLinkList()
{
    link_list_t p=(link_list_t)malloc(sizeof(link_node_t));
    if (p==NULL)
    {
        perror("malloc err");
        return NULL;
    }
    p->next=NULL;
    return p;
}
//4.求单向链表长度的函数
int LengthLinkList(link_node_t *p)
{
    int len=0;
    while (p->next!=NULL)
    {
        p=p->next;
        len++;
    }
    return len;
}
//2.向单向链表的指定位置插入数据
//p保存链表的头指针 post 插入的位置 data插入的数据
int InsertIntoPostLinkList(link_node_t *p,int post, datatype data)
{
    if(post<0||post>LengthLinkList(p))
    {
        perror("InsertIntoPostLinkList err\n");
        return -1;
    }
    for (int i=0;i<post;i++)
    {
        p=p->next;
    }
    link_list_t pnew=(link_list_t)malloc(sizeof(link_node_t));
    if(pnew==NULL)
    {
        perror("error");
        return -1;
    }
    pnew->data=data;
    pnew->next=NULL;
    pnew->next=p->next;
    p->next=pnew;
    return 0;
}
//6.判断单向链表是否为空 1代表空 0代表非空
int IsEpLinkList(link_node_t *p)
{
    return p->next==NULL;
}
//5.删除单向链表中指定位置的数据 post 代表的是删除的位置
int DeletePostLinkList(link_node_t *p, int post)
{
    if(IsEpLinkList(p)||post<0||post>=LengthLinkList(p))
    {
        perror("DeletePostLinkList err\n");
        return -1;
    }
    for (int i=0;i<post;i++)
    {
        p=p->next;
    }
    link_list_t pdel=p->next;
    p->next=pdel->next;
    free(pdel);
    pdel=NULL;
    return 0;
}
//3.遍历单向链表
void ShowLinkList(link_node_t *p)
{
    while (p->next!=NULL)
    {
        p=p->next;
        printf("%d ",p->data);
        
    }
}

//7.修改指定位置的数据 post 被修改的位置 data修改成的数据
int ChangePostLinkList(link_node_t *p, int post, datatype data)
{
    if(IsEpLinkList(p)||post<0||post>=LengthLinkList(p))
    {
        perror("ChangePostLinkList err\n");
        return -1;
    }
    for (int i=0;i<=post;i++)
    {
        p=p->next;
    }
    p->data=data;
    return 0;
}
//8.查找指定数据出现的位置 data被查找的数据 //search 查找
int SearchDataLinkList(link_node_t *p, datatype data)
{
    if(IsEpLinkList(p))
    {
        perror("SearchDataLinkList err\n");
        return -1;
    }
    int n=LengthLinkList(p);
    for (int i=0;i<n;i++)
    {  
         p=p->next;
        if(p->data==data)
        {
            printf("%d ",i);
        }
    }  
    return 0;
}
//11.清空单向链表
void ClearLinkList(link_node_t *p)
{
     link_list_t pdel=NULL;
     while(p->next!=NULL)
     {
         pdel=p->next;
         p->next=pdel->next;
         free(pdel);
         pdel=NULL;
     }
}
//10.转置链表
void ReverseLinkList(link_node_t *p)
{
      link_list_t t;
      link_list_t q;
      q=p->next;
      p->next=NULL;
      while(q)
      {
          t=q;
          q=q->next;
          t->next=p->next; 
          p->next=t;
      }
}
//9.删除单向链表中出现的指定数据,data代表将单向链表中出现的所有data数据删除
int DeleteDataLinkList(link_node_t *p, datatype data)
{
    link_list_t pdel=NULL;
    link_list_t q=p->next;
    while (q!=NULL)
    { 
        if(q->data==data)
        {
         pdel=q;
         p->next=pdel->next;
         free(pdel);
         pdel=NULL;
         q=p->next;
        }
        else
        {
            p=p->next;
            q=p->next;
        }
       } 
       return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
  • 106
  • 107
  • 108
  • 109
  • 110
  • 111
  • 112
  • 113
  • 114
  • 115
  • 116
  • 117
  • 118
  • 119
  • 120
  • 121
  • 122
  • 123
  • 124
  • 125
  • 126
  • 127
  • 128
  • 129
  • 130
  • 131
  • 132
  • 133
  • 134
  • 135
  • 136
  • 137
  • 138
  • 139
  • 140
  • 141
  • 142
  • 143
  • 144
  • 145
  • 146
  • 147
  • 148
  • 149
  • 150
  • 151
  • 152
  • 153
  • 154
  • 155
  • 156
  • 157
  • 158
  • 159
  • 160
  • 161
  • 162
  • 163
  • 164
  • 165
  • 166
  • 167
  • 168

总结：
顺序表和链表的区别？
(1)顺序表在内存当中连续存储的(数组)，但是链表在内存当中是不连续存储的，通过指针将数据链接在一起
(2)顺序表的长度是固定的，但是链表长度不固定
(3)顺序表查找方便，但是插入和删除麻烦，链表，插入和删除方便，查找麻烦

双向链表

	
#include <stdio.h>
#include <stdlib.h>
typedef int datatype;
typedef struct node_t
{
	datatype data;//数据域 
	struct node_t *next;//指向下一个节点的指针 next 下一个
	struct node_t *prior;//指向前一个节点的指针 prior 前一个
}link_node_t,*link_list_t;

//将双向链表的头指针和尾指针封装到一个结构体里 
//思想上有点像学的链式队列
typedef struct doublelinklist
{
	link_list_t head; //指向双向链表的头指针
	link_list_t tail; //指向双向链表的尾指针
	int len;
}double_node_t,*double_list_t;
//1.创建一个空的双向链表
double_list_t createEmptyDoubleLinkList()；
//2.向双向链表的指定位置插入数据 post位置， data数据
int insertIntoDoubleLinkList(double_list_t p, int post, datatype data)；
//3.遍历双向链表
void showDoubleLinkList(double_list_t p)；
//4.删除双向链表指定位置的数据
int deletePostDoubleLinkList(double_list_t p, int post)；
//5.判断双向链表是否为空
int isEmptyDoubleLinkList(double_list_t p)；
//6.求双向链表的长度
int lengthDoubleLinkList(double_list_t p)；
//7.查找指定数据出现的位置 data被查找的数据
int searchPostDoubleLinkList(double_list_t p,datatype data)；
//8.修改指定位置的数据,post修改的位置 data被修改的数据
int changeDataDoubleLinkList(double_list_t p,int post, datatype data)；
//9.删除双向链表中的指定数据 data代表删除所有出现的data数据
int deleteDataDoubleLinkList(double_list_t p, datatype data)；

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37

相关操作

#include "linklist.h"

//1.创建一个空的双向链表
double_list_t createEmptyDoubleLinkList()
{
    double_list_t p = (double_list_t)malloc(sizeof(double_node_t));
    if (p == NULL)
    {
        perror("error1\n");
        return NULL;
    }
    p->len = 0;
    p->tail = p->head = (link_list_t)malloc(sizeof(link_node_t));
    if (p->head == NULL)
    {
        perror("error2\n");
        return NULL;
    }
    p->head->next = NULL;
    p->head->prior = NULL;
    return p;
}
//2.向双向链表的指定位置插入数据 post位置， data数据
int insertIntoDoubleLinkList(double_list_t p, int post, datatype data)
{
    link_list_t temp = NULL;
    if (post < 0 || post > p->len)
    {
        perror("error3\n");
        return -1;
    }
    //创建一个新的节点存放数据
    link_list_t pnew = (link_list_t)malloc(sizeof(link_node_t));
    if (pnew == NULL)
    {
        perror("error4\n");
        return -1;
    }
    //初始化节点
    pnew->data = data;
    pnew->next = NULL;
    pnew->prior = NULL;
    //插入链表
    //对插入位置进行判断
    if (post == p->len) //尾插
    {
        p->tail->next = pnew;
        pnew->prior = p->tail;
        p->tail = pnew; //将指针指向此时尾节点
    }
    else //后半段，尾指针
    {
        //1)将temp移动到被插入的位置
        if (post < p->len / 2) //前半段，头指针
        {
            temp = p->head;
            for (int i = 0; i <= post; i++) //从前往后遍历
                temp = temp->next;
        }
        else
        {
            temp = p->tail;
            for (int i = 0; i < p->len - post; i++) //从后往前遍历
                temp = temp->prior;
        }
        //先连后面再连前面
        temp->prior->next = pnew;
        pnew->prior = temp->prior;
        pnew->next = temp;
        temp->prior = pnew;
    }
    p->len++; //链表长度加一
    return 0;
}
//5.判断双向链表是否为空
int isEmptyDoubleLinkList(double_list_t p)
{
    return p->len == 0;
}
//3.遍历双向链表
void showDoubleLinkList(double_list_t p)
{
    if (isEmptyDoubleLinkList(p))
    {
        perror("error5\n");
    }
    else
    {
        link_list_t temp = p->head;
        printf("正向遍历：\n");
        while (temp->next != NULL)
        {
            temp = temp->next;
            printf("%d ", temp->data);
        }
        printf("\n");
        temp = p->tail;
        printf("反向遍历：\n");
        while (temp != p->head)
        {
            printf("%d ", temp->data);
            temp = temp->prior;
        }
    }
}
//4.删除双向链表指定位置的数据
int deletePostDoubleLinkList(double_list_t p, int post)
{
    link_list_t temp = NULL;
    //容错判断
    if (isEmptyDoubleLinkList(p) || post < 0 || post >= p->len)
    {
        perror("error6\n");
        return -1;
    }
    //判断位置
    if (post == p->len - 1) //尾删
    {
        p->tail = p->tail->prior;
        free(p->tail->next);
        p->tail->next = NULL; //将指针指向此时尾节点
    }
    else //后半段，尾指针
    {
        //1)将temp移动到被删除的位置
        if (post < p->len / 2) //前半段，头指针
        {
            temp = p->head;
            for (int i = 0; i <= post; i++) //从前往后遍历
                temp = temp->next;
        }
        else
        {
            temp = p->tail;
            for (int i = 0; i < p->len - post; i++) //从后往前遍历
                temp = temp->prior;
        }
        //删除操作
        temp->prior->next = temp->next;
        temp->next->prior = temp->prior;
        free(temp);
        temp = NULL;
    }
    p->len--;
    return 0;
}
//6.求双向链表的长度
int lengthDoubleLinkList(double_list_t p)
{
    return p->len;
}
//7.查找指定数据出现的位置 data被查找的数据
int searchPostDoubleLinkList(double_list_t p, datatype data)
{
    //遍历依次查找数据
    link_list_t q = p->head;
    int n = 0;
    while (q->next != NULL)
    {
        q = q->next;
        if (q->data == data)
            return n;
        n++;
    }
    return -1;
}
//8.修改指定位置的数据,post修改的位置 data被修改的数据
int changeDataDoubleLinkList(double_list_t p, int post, datatype data)
{
    link_list_t temp = NULL;
    if (isEmptyDoubleLinkList(p) || post < 0 || post >= p->len)
    {
        perror("error8\n");
        return -1;
    }
    if (post < p->len / 2) //前半段，头指针
    {
        temp = p->head;
        for (int i = 0; i <= post; i++) //从前往后遍历
            temp = temp->next;
    }
    else
    {
        temp = p->tail;
        for (int i = 0; i < p->len - post; i++) //从后往前遍历
            temp = temp->prior;
    }
    temp->data = data;
    return 0;
}
//9.删除双向链表中的指定数据 data代表删除所有出现的data数据
int deleteDataDoubleLinkList(double_list_t p, datatype data)
{
    link_list_t pdel = NULL;
    link_list_t h = p->head->next;
    while (h != NULL)
    {
        if (h->data == data)
        {
            if (h == p->tail)
            {
                p->tail = p->tail->prior;
                free(p->tail->next);
                p->tail->next = NULL;
            }
            else
            {
                h->prior->next = h->next;
                h->next->prior = h->prior;
                pdel = h;
                h = h->next;
                free(pdel);
                pdel = NULL;
            }
            p->len--;
        }
        else
        {
            h = h->next;
        }
    }
    return 0;
}
int main(int argc, char const *argv[])
{
    double_list_t p = createEmptyDoubleLinkList();
    for (int i = 0; i <= 5; i++)
        insertIntoDoubleLinkList(p, i, i + 1);
    showDoubleLinkList(p);
    printf("\n");
    printf("%d \n", searchPostDoubleLinkList(p, 5));
    deleteDataDoubleLinkList(p, 5);
    while (!isEmptyDoubleLinkList(p))
    {
        deletePostDoubleLinkList(p, 0);
    }
    showDoubleLinkList(p);
    free(p->head);
    p->head = NULL;
    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
  • 106
  • 107
  • 108
  • 109
  • 110
  • 111
  • 112
  • 113
  • 114
  • 115
  • 116
  • 117
  • 118
  • 119
  • 120
  • 121
  • 122
  • 123
  • 124
  • 125
  • 126
  • 127
  • 128
  • 129
  • 130
  • 131
  • 132
  • 133
  • 134
  • 135
  • 136
  • 137
  • 138
  • 139
  • 140
  • 141
  • 142
  • 143
  • 144
  • 145
  • 146
  • 147
  • 148
  • 149
  • 150
  • 151
  • 152
  • 153
  • 154
  • 155
  • 156
  • 157
  • 158
  • 159
  • 160
  • 161
  • 162
  • 163
  • 164
  • 165
  • 166
  • 167
  • 168
  • 169
  • 170
  • 171
  • 172
  • 173
  • 174
  • 175
  • 176
  • 177
  • 178
  • 179
  • 180
  • 181
  • 182
  • 183
  • 184
  • 185
  • 186
  • 187
  • 188
  • 189
  • 190
  • 191
  • 192
  • 193
  • 194
  • 195
  • 196
  • 197
  • 198
  • 199
  • 200
  • 201
  • 202
  • 203
  • 204
  • 205
  • 206
  • 207
  • 208
  • 209
  • 210
  • 211
  • 212
  • 213
  • 214
  • 215
  • 216
  • 217
  • 218
  • 219
  • 220
  • 221
  • 222
  • 223
  • 224
  • 225
  • 226
  • 227
  • 228
  • 229
  • 230
  • 231
  • 232
  • 233
  • 234
  • 235
  • 236
  • 237
  • 238
  • 239
  • 240
  • 241

栈

1.概念：
只能在一端进行插入和删除操作的线性表，进行插入和删除的一端叫做栈顶，另一端叫做栈底。
2.特点：
先入后出，后入先出
FILO,LIFO
顺序栈：seqstack
1）逻辑结构：线性结构
2）存储结构：顺序存储
3）操作:

#ifndef _SEQSTACK_H_
#define _SEQSTACK_H_

typedef struct seqstack
{
	int* data;//指向栈的存储位置
	int maxlen;//保存栈的最大长度
	int top;//称为栈针，用的时候，心里面可以将按照顺序表里的last来使用
			//top 始终代表当前栈内最后一个有效元素的下标
}seqstack_t;
//1.创建一个空的栈
seqstack_t *CreateEpSeqStack(int len);//len代表的是创建栈的时候的最大长度
//2.判断是否为满,满返回1 未满返回0
int	 IsFullSeqStack(seqstack_t *p);
//3.入栈 
int  PushStack(seqstack_t *p, int data);//data代表入栈的数据
//4.判断栈是否为空
int IsEpSeqStack(seqstack_t *p);
//5.出栈 
int PopSeqStack(seqstack_t *p);
//6. 清空栈 
void ClearSeqStack(seqstack_t *p);
//7. 获取栈顶数据(注意不是出栈操作，如果出栈，相当于删除了栈顶数据，只是将栈顶的数据获取到，不需要移动栈针)
int GetTopSeqStack(seqstack_t *p);
//8. 求栈的长度
int LengthSeqStack(seqstack_t *p);
#endif 

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27

相关操作代码

#include<stdio.h>
#include<stdlib.h>
#include "seqstack.h"

seqstack_t *CreateEpSeqStack(int len)
{
    seqstack_t *p=(seqstack_t *)malloc(sizeof(seqstack_t));
    if (p==NULL)
    {
        perror("error1\n");
        return NULL;
    }
    p->maxlen=len;
    p->top=-1;
    p->data =(int *)malloc(sizeof(int)*len);
    if(p->data==NULL)
    {
        perror("p->data malloc err\n");
        return NULL;
    }
    return p;
}
//2.判断是否为满,满返回1 未满返回0
int	 IsFullSeqStack(seqstack_t *p)
{
    return p->top+1==p->maxlen;
}
//3.入栈 
int  PushStack(seqstack_t *p, int data)//data代表入栈的数据
{
    if (IsFullSeqStack(p))
    {
        perror("PushStack err\n");
        return -1;
    }
    p->top++;
    p->data[p->top]=data;
    return 0;
}
//4.判断栈是否为空
int IsEpSeqStack(seqstack_t *p)
{
    return p->top==-1;
}
//5.出栈 
int PopSeqStack(seqstack_t *p)
{
    if(IsEpSeqStack(p))
    {
        perror("PopSeqStack err\n");
        return -1;
    }
    p->top--;
    return p->data[p->top+1];
}
//6. 清空栈 
void ClearSeqStack(seqstack_t *p)
{
    p->top=-1;
}
//7. 获取栈顶数据(注意不是出栈操作，如果出栈，相当于删除了栈顶数据，只是将栈顶的数据获取到，不需要移动栈针)
int GetTopSeqStack(seqstack_t *p)
{
   if(!IsEpSeqStack(p))
      return p->data[p->top];
   return -1;
}
//8. 求栈的长度
int LengthSeqStack(seqstack_t *p)
{
    return p->top+1;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72

链式栈
1）逻辑结构：线性结构
2）存储结构：链式存储
3）操作：

#ifndef _LINKSTACK_H_
#define _LINKSTACK_H_
#include <stdio.h>
#include <stdlib.h>
//入栈和出栈只在第一个节点位置操作
typedef int datatype;
typedef struct linkstack
{
	datatype data;//数据域
	struct linkstack *next;//指针域
}linkstack_t;
//1.创建一个空的栈
void CreateEpLinkStack(linkstack_t **ptop);
//2.入栈   data是入栈的数据
参数上之所以采用二级指针，因为我们要随着入栈添加新的节点作为头，top需要永远指向当前链表的头，
那么修改main函数中的top，我们采用地址传递
int PushLinkStack(linkstack_t **ptop, datatype data);
//3.判断栈是否为空
int IsEpLinkStack(linkstack_t *top);
//4.出栈
datatype PopLinkStack(linkstack_t **ptop);
//5.清空栈
void ClearLinkStack(linkstack_t **ptop);//用二级指针，是因为清空后需要将main函数中的top变为NULL
//6.求栈的长度
int LengthLinkStack(linkstack_t *top);//用一级指针，是因为我只是求长度，不需要修改main函数中top指针的指向
//7.获取栈顶数据,不是出栈,不需要移动main函数中的top，所以用一级指针
datatype GetTopLinkStack(linkstack_t *top);
#endif

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28

相关操作代码

#include<stdio.h>
#include<stdlib.h>
#include "linkstack.h"

//1.创建一个空的栈
void CreateEpLinkStack(linkstack_t **ptop)
{
    *ptop=NULL;
}
//2.入栈   data是入栈的数据
//参数上之所以采用二级指针，因为我们要随着入栈添加新的节点作为头，top需要永远指向当前链表的头，
//那么修改main函数中的top，我们采用地址传递
int PushLinkStack(linkstack_t **ptop, datatype data)
//ptop==&top,*ptop==top;
{
    linkstack_t *pnew=(linkstack_t *)malloc(sizeof(linkstack_t));
    if(pnew==NULL)
    {
        perror("PushLinkStack\n");
        return -1;
    }
    pnew->data=data;
    pnew->next=NULL;
    pnew->next=*ptop;
    *ptop=pnew;
    return 0;
}
//3.判断栈是否为空
int IsEpLinkStack(linkstack_t *top)
{
    return top==NULL;
}
//4.出栈
datatype PopLinkStack(linkstack_t **ptop)
{
    if(IsEpLinkStack(*ptop))
    {
        perror("PopLinkStack err\n");
        return -1;
    }
    linkstack_t *pdel=NULL;
    pdel=*ptop;
    datatype a=pdel->data;
    *ptop=pdel->next;
    free(pdel);
    pdel=NULL;
    return a;
}
//5.清空栈
void ClearLinkStack(linkstack_t **ptop)//用二级指针，是因为清空后需要将main函数中的top变为NULL
{
    // linkstack_t *pdel=NULL;
    // while(*ptop!=NULL)
    // {
    //     pdel=*ptop;
    //     *ptop=pdel->next;
    //     free(pdel);
    //     pdel=NULL;
    // }
    while (!IsEpLinkStack(*ptop))
    {
        PopLinkStack(ptop);
    }
    
}
//6.求栈的长度
int LengthLinkStack(linkstack_t *top)//用一级指针，是因为我只是求长度，不需要修改main函数中top指针的指向
{
    int i=0;
    while (top!=NULL)
    {
        i++;
        top=top->next;
    }
    return i;
}
//7.获取栈顶数据,不是出栈,不需要移动main函数中的top，所以用一级指针
datatype GetTopLinkStack(linkstack_t *top)
{
    if(!IsEpLinkStack(top))
          return top->data;
    return -1;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83

总结：
顺序栈和链式栈的区别？
1）存储结构不同，顺序栈相当于数组，连续；链式栈 链表 内存不连续
2）顺序栈长度受限制，链式栈不会

队列(queue)

1.概念：
只允许在两端进行插入和删除操作的线性表，在队尾插入，在队头删除
2.特点：
先入先出，后入后出
FIFO LILO

顺序队列

1）逻辑结构：线性结构
2）存储结构：顺序存储
3）操作:

#include <stdio.h>
#include <stdlib.h>
#define N 5
typedef int datatype;
typedef struct
{
	datatype data[N];//循环队列的数组
	int rear;//存数据端 rear 后面
	int front;//取数据端 front 前面
}sequeue_t;
//1.创建一个空的队列
sequeue_t *CreateEmptySequeue();
//2.入列 data代表入列的数据
int InSequeue(sequeue_t *p,datatype data);
//3.判断队列是否为满
int IsFullSequeue(sequeue_t *p);
//4.判断队列是否为空
int IsEmptySequeue(sequeue_t *p);
//5.出列 
datatype OutSequeue(sequeue_t *p);
//6.求队列的长度
int LengthSequeue(sequeue_t *p);
//7.清空队列函数
void ClearSequeue(sequeue_t *p);

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24

相关操作代码

#include "sequeue.h"

//1.创建一个空的队列
sequeue_t *CreateEmptySequeue()
{
    sequeue_t *p=(sequeue_t *)malloc(sizeof(sequeue_t));
    if (p==NULL)
    {
        perror("CreateEmptySequeue err\n");
        return NULL;
    }
    p->rear=0;
    p->front=0;
    return p;
}
//3.判断队列是否为满
int IsFullSequeue(sequeue_t *p)
{
    return (p->rear+1)%N==p->front;
}
//2.入列 data代表入列的数据
int InSequeue(sequeue_t *p,datatype data)
{
    if (IsFullSequeue(p))
    {
        perror("InSequeue err\n");
        return -1;
    }
    p->data[p->rear]=data;
    p->rear=(p->rear+1)%N;
    return 0;
}
//4.判断队列是否为空
int IsEmptySequeue(sequeue_t *p)
{
    return p->rear==p->front;
}
//5.出列 
datatype OutSequeue(sequeue_t *p)
{
    if (IsEmptySequeue(p))
    {
        perror("OutSequeue err\n");
        return -1;
    }
    datatype a=p->data[p->front];
    p->front=(p->front+1)%N;
    return a;
}
//6.求队列的长度
int LengthSequeue(sequeue_t *p)
{
     return (p->rear+N-p->front)%N;
}
//7.清空队列函数
void ClearSequeue(sequeue_t *p)
{
    p->rear=p->front;
}
int main(int argc, char const *argv[])
{
    sequeue_t *p=CreateEmptySequeue();
    for (int i=0;i<4;i++)
         InSequeue(p,i);
    while (!IsEmptySequeue(p))
    {
        printf("%d ",OutSequeue(p));
    }
    printf("\n");
    
    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72

链式队列
1）逻辑结构：线性结构
2）存储结构：链式存储
3）操作：

#include <stdio.h>
#include <stdlib.h>
typedef int datatype;
typedef struct node
{
	datatype data;//数据域
	struct node *next;//指针域
}linkqueue_node_t,*linkqueue_list_t;

//linkqueue_list_t p === linkqueue_node_t *
typedef struct//将队列头指针和尾指针封装到一个结构体里
{
	linkqueue_list_t front;//相当于队列的头指针
	linkqueue_list_t rear;//相当于队列的尾指针
	//有了链表的头指针和尾指针，那么我们就可以操作这个链表
}linkqueue_t;
//1.创建一个空的队列
linkqueue_t *CreateEmptyLinkQueue();
//2.入列 data代表入列的数据
int InLinkQueue(linkqueue_t *p,datatype data);
//3.出列 
datatype OutLinkQueue(linkqueue_t *p);
//4.判断队列是否为空
int IsEmptyLinkQueue(linkqueue_t *p);
//5.求队列长度的函数
int LengthLinkQueue(linkqueue_t *p);
//6.清空队列
void ClearLinkQueue(linkqueue_t *p);

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28

相关操作代码

#include "linkqueue.h"

//1.创建一个空的队列
linkqueue_t *CreateEmptyLinkQueue()
{
    linkqueue_list_t pnew=(linkqueue_list_t)malloc(sizeof(linkqueue_list_t));
    if(pnew==NULL)
    {
        perror("CreateEmptyLinkQueue err\n");
        return NULL;
    }
    pnew->next=NULL;
    linkqueue_t *p=(linkqueue_t *)malloc(sizeof(linkqueue_t));
    if(p==NULL)
    {
        perror("CreateEmptyLinkQueue err\n");
        return NULL;
    }
    p->rear=pnew;
    p->front=pnew;
    return p;
}
//2.入列 data代表入列的数据
int InLinkQueue(linkqueue_t *p,datatype data)
{
    linkqueue_list_t pnew=(linkqueue_list_t)malloc(sizeof(linkqueue_node_t));
    if(pnew==NULL)
    {
        perror("InLinkQueue err\n");
        return -1;
    }
    pnew->data=data;
    pnew->next=NULL;
    p->rear->next=pnew;
    p->rear=pnew;
    return 0;
}
//4.判断队列是否为空
int IsEmptyLinkQueue(linkqueue_t *p)
{
    return p->front==p->rear;
}
//3.出列 
datatype OutLinkQueue(linkqueue_t *p)
{
    if (IsEmptyLinkQueue(p))
    {
        perror("OutLinkQueuev err\n");
        return -1;
    }
    linkqueue_list_t pdel=NULL;
    pdel=p->front;
    p->front=pdel->next;
    free(pdel);
    pdel=NULL;
    return p->front->data;
}
//5.求队列长度的函数
int LengthLinkQueue(linkqueue_t *p)
{
    linkqueue_list_t q=p->front;
    int len=0;
    while(q->next!=NULL)
    {
        len++;
        q=q->next;
    }
}
//6.清空队列
void ClearLinkQueue(linkqueue_t *p)
{
    while (!IsEmptyLinkQueue(p))
    {
        OutLinkQueue(p);
    }
}
int main(int argc, char const *argv[])
{
    linkqueue_t *p=CreateEmptyLinkQueue();
    printf("1\n");
    for (int i=0;i<4;i++)
        InLinkQueue(p,i);
    printf("2\n");
    while(!IsEmptyLinkQueue(p))
    {
        printf("%d ",OutLinkQueue(p));
    }
    free(p);

    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/IT小白/article/detail/397294
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号