机械臂手眼标定realsense d435相机——眼在手上python、matlab_进行机械臂手眼标定前,需要标定realsense相机吗

作者：IT小白 | 2024-04-29 16:33:27

踩

进行机械臂手眼标定前,需要标定realsense相机吗

两周内看了好多博客，博客上的代码甚至github上的代码都试过了一遍，各种语言matlab、c++、python，了解到了许多做手眼标定的平台——halcon、ros（这俩还需要从头开始学，时间不太够用），最后看到了鱼香ros的博客，参考了一下并总结完整，附链接

此博客仅记录学习过程总结思路，可以借鉴，有问题可以指出并联系我

基于ROS的机械臂手眼标定-基础使用_鱼香ros手眼标定_鱼香ROS的博客-CSDN博客

目录

手眼标定原理

获得手眼矩阵X

验证准确性

手眼标定原理

眼在手上，眼在手上的目的是求出末端到相机的变换矩阵X，也成为了手眼矩阵

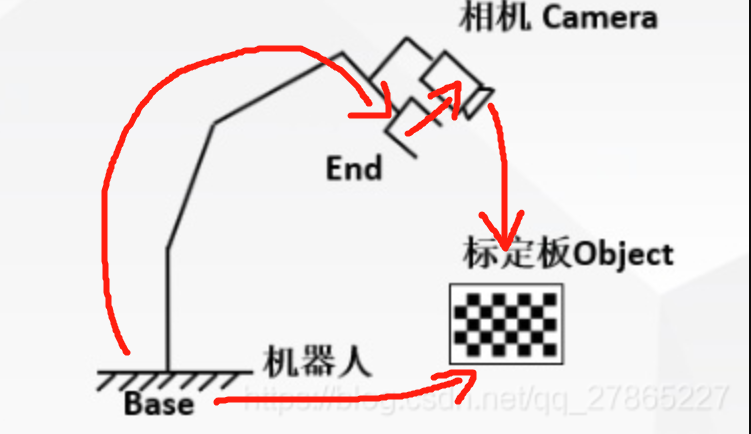
由图可知，

标定板在机械臂坐标系下的位姿=标定板在相机坐标系下的位姿—>相机在末端坐标系下的位姿—>末端在机械臂基坐标系下的位姿

base to end 可以通过机械臂运动学得到

end to camera 是代求的X

camera to object 是通过相机拍下标定板照片得到

$T^{_{base}^{board}}=T^{_{camera}^{board}}*T^{_{end}^{camera}}*T^{_{base}^{end}}$

只要有两组数据，就可以列恒等式

$T^{_{camera}^{board}}_{1}*T^{_{end}^{camera}}_{1}*T^{_{base}^{end}}_{1}=T^{_{camera}^{board}}_{2}*T^{_{end}^{camera}}_{2}*T^{_{base}^{end}}_{2}$

除了X外，剩下的矩阵都可通过以上手法求得，通过数学方法移项后就是我们常说的AX=XB

接下来的目的就是求得X

获得手眼矩阵X

eyeinhandcalibrate.py


def get_matrix_eular_radu(x, y, z, rx, ry, rz):
    rmat = tfs.euler.euler2mat(math.radians(rx), math.radians(ry), math.radians(rz))
    rmat = tfs.affines.compose(np.squeeze(np.asarray((x, y, z))), rmat, [1, 1, 1])
    return rmat
 
 
def skew(v):
    return np.array([[0, -v[2], v[1]],
                     [v[2], 0, -v[0]],
                     [-v[1], v[0], 0]])
 
 
def rot2quat_minimal(m):
    quat = tfs.quaternions.mat2quat(m[0:3, 0:3])
    return quat[1:]
 
 
def quatMinimal2rot(q):
    p = np.dot(q.T, q)
    w = np.sqrt(np.subtract(1, p[0][0]))
    return tfs.quaternions.quat2mat([w, q[0], q[1], q[2]])
 
 
# hand = [1.1988093940033604, -0.42405585264804424, 0.18828251788562061, 151.3390418721659, -18.612399542280507,
#         153.05074895025035,
#         1.1684831621733476, -0.183273375514656, 0.12744868246620855, -161.57083804238462, 9.07159838346732,
#         89.1641128844487,
#         1.1508343174145468, -0.22694301453461405, 0.26625166858469146, 177.8815855486261, 0.8991159570568988,
#         77.67286224959672]
hand = [
 
    # -0.05448,-0.15018,0.06552,89.61059916,-2.119943842,-1.031324031,
    #     -0.10149,-0.23025,0.04023,96.7725716,6.187944187,5.328507495,
    #     -0.10114,-0.2207,0.04853,97.00175472,5.729577951,1.375098708    毫米单位
 
-54.48,	-150.18,	65.52,  89.61059916,    -2.119943842,   -1.031324031,
-101.49,-230.25,    40.23,  96.7725716,      6.187944187,    5.328507495,
-101.14,-220.7	,   48.53,  97.00175472,    5.729577951,    1.375098708
 
        ]
 
# camera = [-0.16249272227287292, -0.047310635447502136, 0.4077761471271515, -56.98037030812389, -6.16739631361851,
#           -115.84333735802369,
#           0.03955405578017235, -0.013497642241418362, 0.33975949883461, -100.87129330834215, -17.192685528625265,
#           -173.07354634882094,
#           -0.08517949283123016, 0.00957852229475975, 0.46546608209609985, -90.85270962096058, 0.9315977976503153,
#           175.2059707654342]
 
camera = [
 
    # -0.0794887,-0.0812433,0.0246,0.0008,0.0033,0.0182,
    #       -0.078034,-0.0879632,0.4881494,-0.1085,0.0925,-0.1569,
    #       -0.1086702,-0.0881681,0.4240367,-0.1052,0.1251,-0.1124,
-79.4887,	-81.2433,	24.6,        0.0008,     0.0033,     0.0182,
-78.034,	-87.9632,	488.1494,    -0.1085,    0.0925,     -0.1569,
-108.6702,	-88.1681,	424.0367,    -0.1052,    0.1251,     -0.1124,
 
 
          ]
 
Hgs, Hcs = [], []
for i in range(0, len(hand), 6):
    Hgs.append(get_matrix_eular_radu(hand[i], hand[i + 1], hand[i + 2], hand[i + 3], hand[i + 4], hand[i + 5],))
    Hcs.append(
        get_matrix_eular_radu(camera[i], camera[i + 1], camera[i + 2], camera[i + 3], camera[i + 4], camera[i + 5]))
 
Hgijs = []
Hcijs = []
A = []
B = []
size = 0
for i in range(len(Hgs)):
    for j in range(i + 1, len(Hgs)):
        size += 1
        Hgij = np.dot(np.linalg.inv(Hgs[j]), Hgs[i])
        Hgijs.append(Hgij)
        Pgij = np.dot(2, rot2quat_minimal(Hgij))
 
        Hcij = np.dot(Hcs[j], np.linalg.inv(Hcs[i]))
        Hcijs.append(Hcij)
        Pcij = np.dot(2, rot2quat_minimal(Hcij))
 
        A.append(skew(np.add(Pgij, Pcij)))
        B.append(np.subtract(Pcij, Pgij))
MA = np.asarray(A).reshape(size * 3, 3)
MB = np.asarray(B).reshape(size * 3, 1)
Pcg_ = np.dot(np.linalg.pinv(MA), MB)
pcg_norm = np.dot(np.conjugate(Pcg_).T, Pcg_)
Pcg = np.sqrt(np.add(1, np.dot(Pcg_.T, Pcg_)))
Pcg = np.dot(np.dot(2, Pcg_), np.linalg.inv(Pcg))
Rcg = quatMinimal2rot(np.divide(Pcg, 2)).reshape(3, 3)
 
A = []
B = []
id = 0
for i in range(len(Hgs)):
    for j in range(i + 1, len(Hgs)):
        Hgij = Hgijs[id]
        Hcij = Hcijs[id]
        A.append(np.subtract(Hgij[0:3, 0:3], np.eye(3, 3)))
        B.append(np.subtract(np.dot(Rcg, Hcij[0:3, 3:4]), Hgij[0:3, 3:4]))
        id += 1
 
MA = np.asarray(A).reshape(size * 3, 3)
MB = np.asarray(B).reshape(size * 3, 1)
Tcg = np.dot(np.linalg.pinv(MA), MB).reshape(3, )
print(tfs.affines.compose(Tcg, np.squeeze(Rcg), [1, 1, 1]))

其中，hand为基坐标系下夹爪的位姿，一般从示教器上获取，我用的是ur5机械臂，注意单位mm和rad

三行为三组数据，hand=(x,y,z,rx,ry,rz)，同时应将弧度制转为角度制

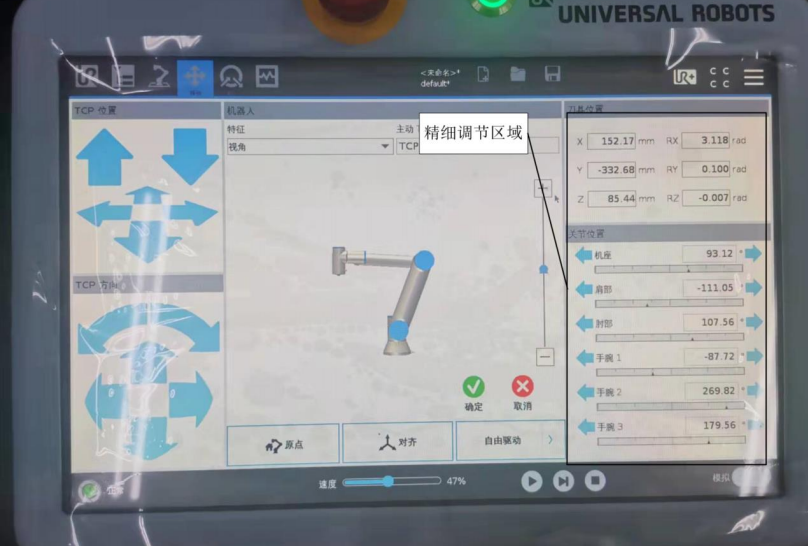
camera后输入的为相机的外参（平移向量和旋转矩阵），相机中标定板的位姿

三行为三组数据，camera=(x,y,z,rx,ry,rz)，同时应将弧度制转为角度制

我是使用matlab工具包对相机外参进行标定的

注：得到的旋转向量应转为旋转矩阵，再转为欧拉角，Python、matlab代码见如下链接

手眼标定必备——旋转向量转换为旋转矩阵python——罗德里格斯公式Rodrigues_邸笠佘司的博客-CSDN博客

输出的即为手眼标定矩阵X


[[ 9.97623261e-01 -4.70586261e-02  5.03320417e-02  9.72987830e+02]
 [ 4.65612713e-02  9.98854765e-01  1.10094003e-02 -1.27118401e+03]
 [-5.07924869e-02 -8.63971002e-03  9.98671857e-01 -4.29111524e+02]
 [ 0.00000000e+00  0.00000000e+00  0.00000000e+00  1.00000000e+00]]

验证准确性

根据手眼标定原理可知，

$T^{_{base}^{board}}=T^{_{camera}^{board}}*T^{_{end}^{camera}}*T^{_{base}^{end}}$

使用理论验证法，使用两组数据用等式将其联立，求得X


clc;
%T1*X*T2 = T3*X*T4 = T5*X*T6
%T1为相机到标定板，T2为基坐标到末端
T1 = [  0.9998   -0.0182    0.0033  -79.4887			
         0.0182    0.9998   -0.0008  -81.2433			
        -0.0033    0.0009    1.0000   24.6000			
            0         0         0      1.0000   ];
 
T2 = [  	 -0.2681   -0.4478   -0.8530  -54.4800				
         -0.3725   -0.7684    0.5205  -150.1800				
         -0.8885    0.4572    0.0392   65.5200				
            0         0         0       1.0000];
 
T3 = [ 0.9835    0.1556    0.0924  -78.0340			
   -0.1652    0.9803    0.1078  -87.9632			
   -0.0738   -0.1213    0.9899  488.1494			
         0         0         0    1.0000 ];
 
T4 = [  0.5753    0.8124   -0.0951 -101.4900				
    0.6340   -0.5163   -0.5758 -230.2500				
   -0.5169    0.2709   -0.8120   40.2300				
         0         0         0    1.0000  	]  ;
 
T5 =   [ 0.9859    0.1113    0.1248 -108.6702			
   -0.1246    0.9867    0.1042  -88.1681			
   -0.1115   -0.1183    0.9867  424.0367			
 0         0         0    1.0000	] 	;
 
T6 = [  0.1654   -0.8344   -0.5258 -101.1400			
   -0.9468    0.0149   -0.3215 -220.7000			
    0.2761    0.5510   -0.7875   48.5300			
         0         0         0    1.0000 		
];
 
%X = [[ 0.997623261 -0.0470586261  0.0503320417  972.987830]						
%     [ 0.0465612713  0.998854765  0.0110094003 -1271.18401]						
 %    [-0.0507924869 -0.00863971002  0.998671857 -429.111524]						
  %   [ 0  0  0  1]]						
 
%ans1 = T1*X*T2
%ans2 = T3*X*T4
%ans3 = T5*X*T6
 
T1*X*T2==T3*X*T4
X

结果如下


X =
   1.0e+03 *
    0.0010   -0.0000    0.0001    0.9730
    0.0000    0.0010    0.0000   -1.2712
   -0.0001   -0.0000    0.0010   -0.4291
         0         0         0    0.0010

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/IT小白/article/detail/508676