一篇文章带你搞懂动态规划（由暴力递归到动态规划）

由递归到动态规划

---

思想

”动态规划“的过程相当于记忆化搜索， 即在普通递归的过程中用二维数组进行记忆化存储一些状态结果， 从而避免重复的计算（剪枝）。

举一个简单的例子：在递归法求解斐波那契数列的过程中， 就进行了多次的重复计算， 而动态规划相当于是对已经计算的状态结果进行存储， 从而在调用的时候直接返回结果即可

​ $$f(n)=f(n-1)+f(n-2)$$

DP分析思路如下：

---

1. 我们需要根据题意建立一个简单的暴力递归过程

2. 所以这里，我们初步的优化思路：

在遍历到某一个状态时：

• 若是此状态已经在之前算过， 那么直接返回结果即可
• 若是此状态之前没算过， 那么调用递归函数进行计算， 并将状态记忆存储， 然后返回结果

3. 具体记忆化存储状态的过程可以看成是一个打表填表的递推过程，由已有递归转移推未知来进行状态表的填充，从而转换为最终的DP

---

观看左神动态规划心得
文章会持续更新， 总结各种dp相关题型加入

具体题目:

一、机器人到达指定位置方法数

点击此处跳转：机器人达到指定位置方法数

一、暴力递归分析

#include <iostream>
using namespace std;
const int len = 5010;

int process1(int cur, int rest, int aim,
             int N) {   //cur:当前位置，需要走的步数， 目标位置， 位置数量
    if (rest == 0)   return cur == aim ? 1 : 0;
    if (cur == 1) return process1(cur + 1, rest - 1, aim, N);
    if (cur == N) return process1(cur - 1, rest - 1, aim, N);
    return process1(cur + 1, rest - 1, aim, N) +  process1(cur - 1, rest - 1, aim,
            N);
}

int ways1(int N, int start, int K,
          int dest) {  //位置数量， 开始位置，需要走的步数， 目的地位置
    return process1(start, K, dest, N);
}

int main() {
    int N, M, K, P;
    cin >> N >> M >> K >> P;
    cout << ways1(N, M, K, P);

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

二、《剪枝》记忆化存储

#include <iostream>
#include <cstring>
using namespace std;
const int len = 5010;
const int mod = 1e9 + 7;
int N, M, K, P;
int f[len][len];

int process1(int cur, int rest, int aim, int N,
             int f[len][len]) {  //cur:当前位置，需要走的步数， 目标位置， 位置数量
    if (f[cur][rest] != -1) return f[cur][rest];
    int ans = 0;
    if (rest == 0)   ans = cur == aim ? 1 : 0;
    else if (cur == 1) ans = process1(cur + 1, rest - 1, aim, N, f);
    else if (cur == N) ans = process1(cur - 1, rest - 1, aim, N, f);
    else ans = process1(cur + 1, rest - 1, aim, N, f) +  process1(cur - 1, rest - 1,
                   aim, N, f);
    f[cur][rest] = ans;
    return ans;
}

int ways1(int N, int start, int K,
          int dest) {  //位置数量， 开始位置，需要走的步数， 目的地位置

    memset(f, -1, sizeof f);
    return process1(start, K, dest, N, f);
}

int main() {

    cin >> N >> M >> K >> P;
    long long ans = (long long)ways1(N, M, K, P) % mod;
    cout << ans;

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

三、递归转DP， 由状态方程打表

#include <iostream>
#include <cstring>
using namespace std;
const int len = 5010;
const int mod = 1e9 + 7;
int N, M, K, P;
int f[len][len];

int ways1(int N, int start, int K,
          int dest) {  //位置数量， 开始位置，需要走的步数， 目的地位置
    memset(f, 0, sizeof f);
    f[dest][0] = 1;
    for(int rest = 1; rest <= K; rest++) {
        f[1][rest] = f[2][rest - 1];
        for(int cur = 2; cur < N; cur++) {
            f[cur][rest] = (f[cur-1][rest-1] + f[cur+1][rest-1]) % mod;
        }
        f[N][rest] = f[N - 1][rest - 1];
    }
    return f[start][K];
}

int main() {

    cin >> N >> M >> K >> P;
    int ans = ways1(N, M, K, P) % mod;
    cout << ans;

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

二、排成一条线的纸牌博弈问题

点击此处跳转：排成一条线的纸牌博弈问题

第一步：暴力递归

代码如下：

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 5010;
int a[N], n;
int g(int a[], int L, int R);
int f(int a[], int L, int R);
//先手获得的最好分数返回
int f(int a[], int L, int R) {
    //若此时只剩一个数， 那么先手必定得到此数
    if (L == R)  return a[L];
    //若是先手取左边， 则剩余的[L +1, R]只能作为后手
    int p1 = a[L] + g(a, L + 1, R);
    //若是先手取右边， 则剩余的[L, R - 1]只能作为后手
    int p2 = a[R] + g(a, L, R - 1);
    //先手选取对自己最优情况
    return max(p1, p2);
}
//后手获得的最好分数返回
int g(int a[], int L, int R) {
    //若此时只剩一个数， 那么先手必定得到此数， 而后手就只能得到0
    if(L == R)  return 0;
    //若先手已经选取左边， 则此时后手在[L + 1, R]充当先手
    int p1 = f(a, L + 1, R);
    //若先手已经选取右边， 则此时后手在[L, R - 1]充当先手
    int p2 = f(a, L, R - 1);
    //因为决定权在于先手， 这里留给后手的只能是两种最优情况的较次者
    return min(p1, p2);
}
//返回获胜者的分数
int win1(int a[]) {
    if (a == NULL || n == 0) return 0;
    int front = f(a, 0, n - 1);
    int back = g(a, 0, n - 1);
    return max(front, back);
}
int main() {
    cin >> n;
    for (int i = 0; i < n; i++)  cin >> a[i];
    cout << win1(a);
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

这里可以看到普通的递归会直接超时

接下来进行记忆化存储状态， 省去重复计算步骤
1

第二步：递归转动态规划

这里的转换计算过程对应于：

这里进行初始化构建两个表：fmap 和 gmap 来存储状态， 进行优化， 分析取值范围， 在每次调用的时候加入两个表， 且在每次调用函数的时候返回当前状态值， 且如果没有计算过当前状态的话， 那么进行计算并更新此状态

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 5010;
int a[N], n;
//这里进行构建两个表分别来来存储先手和后手得分状态
int g(int a[], int L, int R, int fmap[][N], int gmap[][N]);
int f(int a[], int L, int R, int fmap[][N], int gmap[][N]);
//先手获得的最好分数返回
int f(int a[], int L, int R, int fmap[][N], int gmap[][N]) {
    if (fmap[L][R] != -1)    return fmap[L][R]; 
    int ans = 0;								
    //若此时只剩一个数， 那么先手必定得到此数
    if (L == R)  ans = a[L];
    else {
        //若是先手取左边， 则剩余的[L +1, R]只能作为后手
        int p1 = a[L] + g(a, L + 1, R, fmap, gmap);
        //若是先手取右边， 则剩余的[L, R - 1]只能作为后手
        int p2 = a[R] + g(a, L, R - 1, fmap, gmap);
        //先手选取对自己最优情况
        ans = max(p1, p2);
    }
    //将答案存储，更新状态
    fmap[L][R] = ans;						    
    return ans;
}
//后手获得的最好分数返回
int g(int a[], int L, int R, int fmap[][N], int gmap[][N]) {
    if (gmap[L][R] != -1)    return gmap[L][R];
    int ans = 0;
    //这里不需要考虑L==R情况，因为ans本身就等于0了
    if (L != R) {
        //若先手已经选取L， 则此时后手在[L + 1, R]充当先手
        int p1 = f(a, L + 1, R, fmap, gmap);
        //若先手已经选取R， 则此时后手在[L, R - 1]充当先手
        int p2 = f(a, L, R - 1, fmap, gmap);
        //因为决定权在于先手， 这里留给后手的只能是两种最优情况的较次者
        ans = min(p1, p2);
    }
    gmap[L][R] = ans;
    return ans;
}
//返回获胜者的分数
int win2(int a[]) {
    if (a == NULL || n == 0) return 0;
    //首先对"表"进行初始化， 若是某个状态还没有进行计算， 则赋值为 -1
    int fmap[n][n], gmap[n][n];
    memset(fmap, -1, sizeof fmap);
    memset(gmap, -1, sizeof gmap);
    int front = f(a, 0, n - 1, fmap, gmap);
    int back = g(a, 0, n - 1, fmap, gmap);
    return max(front, back);
}
int main() {
    cin >> n;
    for (int i = 0; i < n; i++)  cin >> a[i];
    cout << win2(a);
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

此时的提交结果：

在这里有一个==细节==：

*二维数组作为函数参数*

​ 规定：如果将二维数组作为参数传递给函数，那么在函数的参数声明中必须指明数组的列数，数组的行数没有太大关系，可以指定也可以不指定。因为函数调用时传递的是一个指针，它指向由行向量够成的一维数组。因此二维数组作为函数参数正确写法如下所示：

void Func(int array[3][10]);

void Func(int array[ ][10]);

但是不能把第二维或者更高维的大小省略，如下面的定义是不合法的：

void Func(int array[ ][ ]);

因为从实参传递来的是数组的起始地址，在内存中按数组排列规则存放(按行存放)，而并不区分行和列，如果在形参中不说明列数，则系统无法决定应为多少行多 少列，不能只指定一维而不指定第二维，下面写法是错误的：

void Func(int array[3][]);

---

第三步：状态转移打表

下半部分L < R都没用， 只需上半部分， 两个表互相关联，且通过对角线的两元素互相推

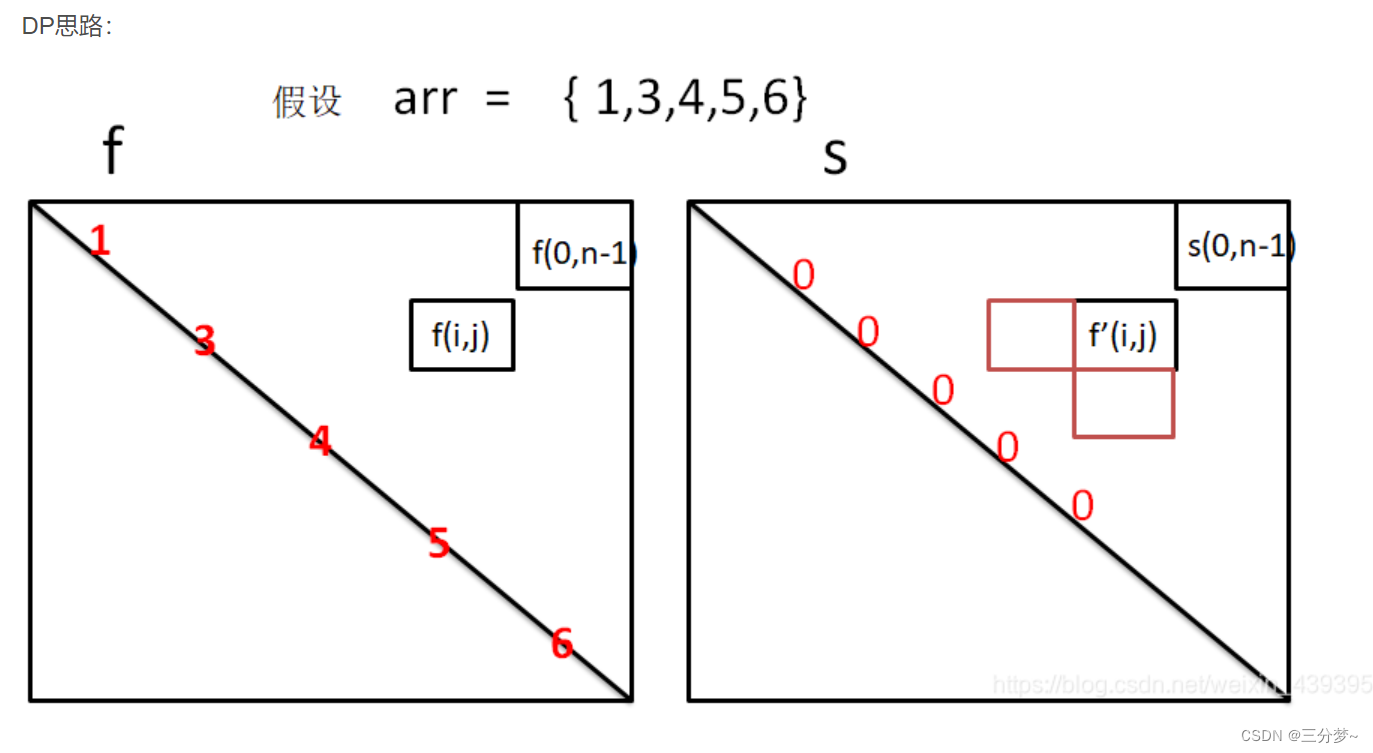
代码如下：

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 5010;
int a[N], n;
int win3(int a[]) {
   if (a == NULL || n == 0) return 0;
   int fmap[n][n], gmap[n][n];
   //int front = f(a, 0, n - 1, fmap, gmap);
   //int back = g(a, 0, n - 1, fmap, gmap);
   //return max(front, back);
   for (int i = 0; i < n; i++)  fmap[i][i] = a[i];
   for (int j = 0; j < n; j++)  gmap[j][j] = 0;
   //根据列（R）进行一步步计算推进，一个一个对角线进行赋值famp和gmap
   for (int startCol = 1; startCol < n; startCol++) {
       int L = 0;
       int R = startCol;
       while (R < n) {
           fmap[L][R] = max(a[L] + gmap[L + 1][R], a[R] + gmap[L][R - 1]);
           gmap[L][R] = min(fmap[L + 1][R], fmap[L][R - 1]);
           L++;
           R++;
       }
   }
   return max(fmap[0][n - 1], gmap[0][n - 1]);
}
int main() {
   cin >> n;
   for (int i = 0; i < n; i++)  cin >> a[i];
   cout << win3(a);
   return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

最后的提交结果如下：

最后， 这里对于后手拿取的问题可以模拟下加深理解：

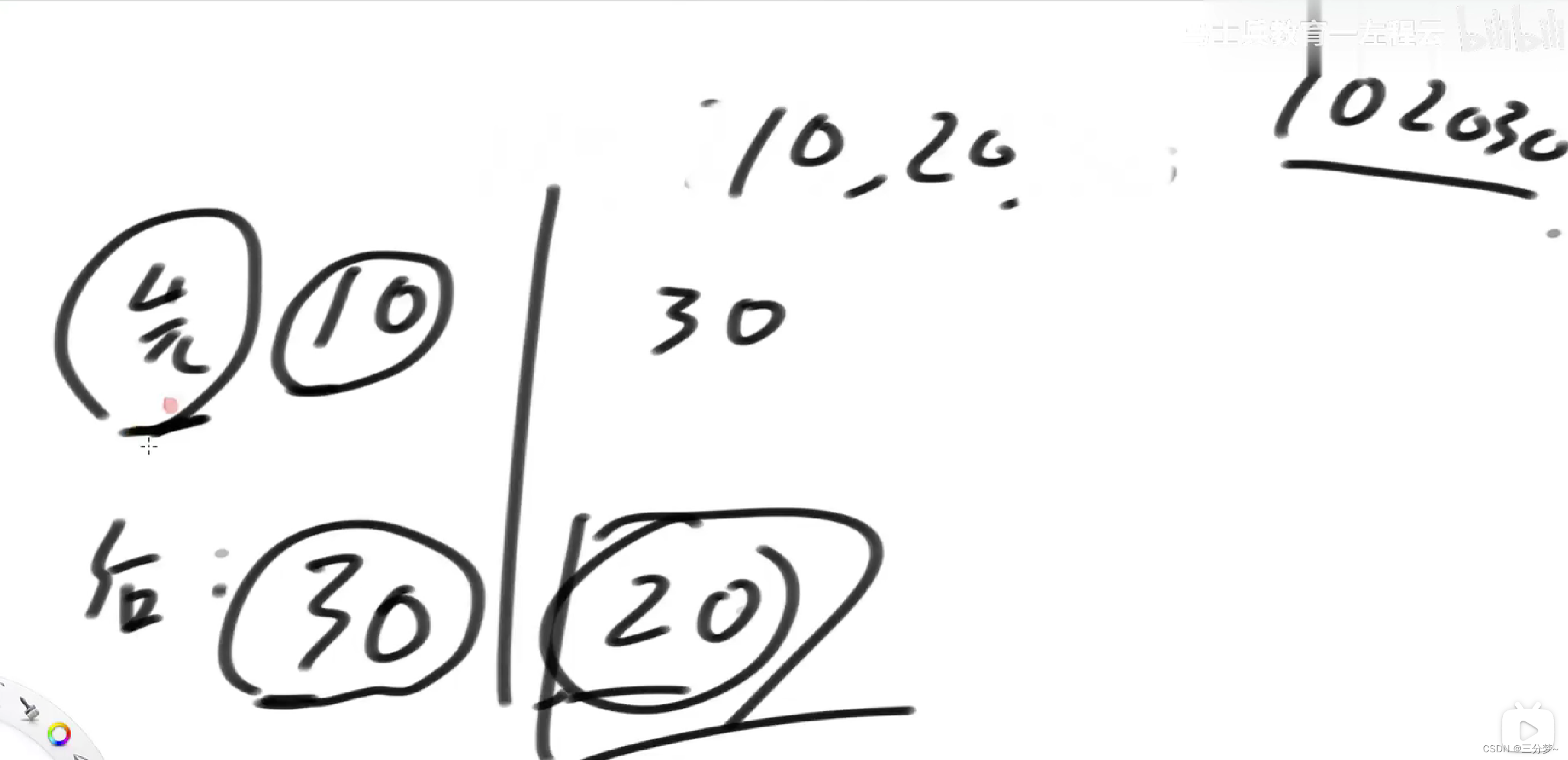
假设所给为[10, 20, 30]

后手会在两次最优中被动拿走较次的， 原因如下：

两种情况： 先手 - > 10， 后手 - > 30 || 先手 - > 30， 后手 - > 20

这里因为最优策略， 先手肯定会聪明的选取好的方案， 把较次的留给后手（20）

三、背包问题

点击此处跳转：01背包问题

​

在逐渐掌握后可以缩减为两步直接解决， 省去中间一步

第一步：递归模拟

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1010;
int w[N], v[N], n, bag;
int process(int w[], int v[], int index, int bag);
int maxValue(int w[], int v[], int bag);

int maxValue(int w[], int v[], int bag) {
	if(w == NULL || v == NULL || n == 0)	return 0;
	return process(w, v, 0, bag);
}
//返回最大价值 
int process(int w[], int v[], int index, int rest) {	//重量、价值、当前位置、背包容量 
	if(index == n)	return 0;
	if(rest < 0)	return 0;	//背包容量可以为0， 因为货物重量可能为0，而<0则为无效 
	//有货， index位置的货
	//bag有空间 >= 0
	//此时两种选择， 选 或 不选
	//1.不要
	int p1 = process(w, v, index + 1, rest);
	//2.要（判断是否装得下）
	int p2 = 0;
	if(rest >= w[index])
		p2 = v[index] + process(w, v, index + 1, rest - w[index]);
	return max(p1, p2);
} 

int main() {
	cin >> n >> bag;
	for(int i = 0; i < n; i++) {
		cin >> w[i] >> v[i];
	}
	
 	cout << maxValue(w, v, bag);	//超时TLE
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

提交结果：

第二步：转DP

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1010;
int w[N], v[N], n, bag;

int dp(int w[], int v[], int bag) {
    if(w == NULL || v == NULL || n == 0)	return 0;
    int dp[N][N];
    for(int i = 0; i <= bag; i++)   dp[n][i] = 0;
    for(int idx = n - 1; idx >= 0; idx--) {
        //这里每个状态只依赖下一行(idx + 1)的数据， 而和同行的无关， 故顺序都可
        for(int rest = 0; rest <= bag; rest++) {
            //不取当前
            int p1 = dp[idx + 1][rest];
            //取当前
            int p2 = 0;
            if(rest >= w[idx])
                p2 = v[idx] + dp[idx + 1][rest - w[idx]];
            dp[idx][rest] = max(p1, p2);
        }
    }
    return dp[0][bag];	//因为是从 n-1 递推到 0， 故 0 即为最终答案
}

int main() {
	cin >> n >> bag;
	for(int i = 0; i < n; i++) 		cin >> w[i] >> v[i];
// 	cout << maxValue(w, v, bag);	上一步的会超时TLE
    cout << dp(w, v, bag);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

提交结果：

此题发现在构建dp表的时候， 两个变量 index （当前位置）和 bag（当前背包容量）， 每个状态只依赖于index + 1，而不依赖于同行其他， 故可以由二维数组继续优化为一维数组存储状态即可， 具体代码如下：

一维优化版：

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1005;
int f[N];
int main()
{
    int n,m;
    cin >> n >> m;
    for(int i = 1;i <= n;i++)
    {
     int v,w;
     cin >> v >> w;
     for(int j = m;j >= v;j--)
     f[j] = max(f[j],f[j - v] + w);     //容量为j时的最大价值  
    }
    cout << f[m] << endl;    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

提交结果：

四、数字字符串转换为字母组合的种数

点击链接跳转：数字字符串转换为字母组合的种数

题目如下：

思路：

考虑边界情况， 从 0 ~ n - 1位置进行遍历， 无需进行转换操作

• 若 i == str.length()， 则代表能跑通， 之前的遍历操作成立， 可构成一种方案数
• 若 在转换操作过程中遍历到单个0，即此处跑不通， 断路不成

在判断完特殊情况后， 正常的 分为 i单转和 i & i+1组合转

• i单转：成立那么直接进行下一个位置的操作， process(str, i + 1);
• 组合转：若是可组成符合条件的组合， 那么直接进行第i + 2的位置的继续操作即可

第一步：递归

#include <iostream>
#include <string>
using namespace std;
string str;
// str[0...n-1]转换无需过问
// str[i...]去转换， 返回方案数
int process(string str, int i) {
    if (i == str.length())   return 1;  //能到这儿说明之前都能跑通符合成立， 可构成一种方案数
    if (str[i] == '0')   return	0;  //若是当前位置所指为'0'， 则代表跑不通
    //str[i] ！= 0
    //可能性一： i单转
    int ways = process(str, i + 1); //成立那么直接操作下一个
    //可能性二：i 与 i+1 进行组合
    if (i + 1 < str.length() && ((str[i] - '0') * 10 + str[i + 1] - '0' < 27) ) {
        ways += process(str, i + 2);
    }
    return ways;
}
//str只含有[0, 9]，
//返回多少种转换方案
int way1(string str) {
    if (str == "")   return 0;
    return process(str, 0); //从下标为0开始递推
}

int main() {
    cin >> str;
    cout << way1(str);
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

第二步：转DP

观察尝试递归推导式可得：每个位置的状态依赖于后边的式子， 即填表需要从后往前依次递推转移

#include <iostream>
#include <string>
#include <cstring>
using namespace std;
const int mod = 1e9 + 7;
string str;
int dp(string str) {
	if(str == "")	return 0;
	int N =	str.length() + 1; 
	int dp[N];
	memset(dp, 0, sizeof dp);
	dp[N] = 1;
	//因为每个位置状态依赖于后边的， 故从后往前状态转移 
	for(int i = N - 1; i >= 0; i--) {
		if(str[i] == '0')	dp[i] = 0;	//可省略 
		else {
			int ways = dp[i + 1] % mod;
			if(i + 1 < str.length() && ((str[i] - '0') * 10 + str[i + 1] - '0' < 27) ) {
			ways += dp[i + 2] % mod;
			}
			dp[i] = ways;	//更新表 
		}
	}	
	return dp[0];	//因为是从后往前递推 
}

int main() {
	
	cin >> str;
//	cout << way1(str);
	cout << dp(str) % mod;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

提交结果：

---

后续更新ing