Li_阴宅

这个屌丝很懒，什么也没留下！

热门标签

OpenFOAM学习笔记_openfoam欧拉离散方案

作者：Li_阴宅 | 2024-07-09 04:09:43

踩

openfoam欧拉离散方案

OpenFOAM

计算流体力学：用计算机求解流体控制方程，来模拟真实情况下，流体的流动状态
OpenFOAM的离散方法：有限体积法，将整个空间划分成若干个控制体
OpenFOAM使用的网格系统：同位网格（Collocated grid system），即速度场和压力场定义在相同的网格中
OpenFOAM中snappyHexMesh使用的网格类型：snappyHexMesh生成贴体六面体网格，OpenFOAM使用的网格是非结构网格
耦合是指两个或两个以上的体系或两种运动形式间通过相互作用而彼此影响以至联合起来的现象。解耦就是用数学方法将两种运动分离开来处理问题，常用解耦方法就是忽略或简化对所研究问题影响较小的一种运动，只分析主要的运动。
使用同位网格的话，速度场和压力场会发生解耦现象，为了解决这种问题，通常使用Rhie-Chow差分格式来解决震荡解的问题。
错位网格在复杂几何体中使用起来不是很顺畅。
pimpleFoam：大步长瞬态求解器，使用PISO-SIMPLE算法，一般结合动网格使用。
连续方程是一个质量守恒方程，描述了不可压流体的体积守恒，这是一个椭圆型方程，因为其涉及到速度的二阶导数。
动量方程描述了流体的动量守恒，包括流体的加速度、粘性和压力。由于包含一阶时间导数和二阶空间导数，因此它是一个抛物线型方程。
OpenFOAM中的压力一般指的是静压。
血液粘度为0.0035kg/(m*s) 密度为1060kg/m3
ExecutionTime 是CPU 时间，指CPU执行代码花费的时间。 ClockTime 是墙上时钟时间（ wall-clock time ），指物理世界中花费的时间。
网格准备：从CT->STL->边界面划分算法->GMSH生成.msh文件-> MMG upgrade .msh文件
在OpenFOAM中，internalField是指在模拟开始时，场变量（如速度、压力等）在计算域内的初始值。它的设置是必要的，因为在模拟开始时，计算域中的场变量必须有一个初始值，以便开始迭代计算。如果没有设置internalField，OpenFOAM将使用默认值作为初始值，这可能会导致模拟结果不准确或不符合预期。因此，设置internalField可以确保模拟开始时场变量的初始状态正确，并且能够得到准确的模拟结果。
若要求解一个微分方程，需要有初始条件和边界条件。在OpenFOAM中internalField定义初始条件，它可以是均匀的或不均匀的，boundaryField定义边界条件，这是数学边界条件，如固定值或zeroGradient

OpenFOAM学习资源

OpenFOAM快捷命令之foamGet：

可以展示字典文件的编写样例，比如用户不知道topoSetDict字典文件如何编写，可以使用以下命令直接生成topoSetDict字典文件的样例：

foamGet topoSetDict
1

OpenFOAM库函数

lib文件夹下的.so代表编译好的库函数
src文件加下存放的是库函数，实现不同的openfoam功能

ODE包含与常微分方程有关的库函数
dynamicFvMesh 动网格相关的
postProcessing 后处理相关
transportModels 传输模型相关的
sixDoFRigidBodymotion 六自由度运动相关的
TurbulenceModels 湍流模型相关的
thermophysicalModels为热力学模型
OpenFOAM为最核心的库
FiniteVolume 有限体积法相关的(网格离散运算符矩阵求解器等) 几乎用于所有求解器

OpenFOAM项目目录

OpenFOAM项目目录包含
- 源代码
- 可执行程序
源代码
- wmake ：为编译工具平台代码 OpenFOAM自带编译工具平台
- etc：项目的整体配置
- src：类库代码，所有在此的代码都会编译成动态链接库so
- application：为应用代码，所有在此的代码都会编译成可执行的程序
- tutorials：案例代码，教如何使用application生成的程序计算案例的模板
- COPYING、README为版权声明
可执行程序
- bin：为执行的脚本
- platforms：为二进制文件，即编译后的文件目录，编译要求不同，目录不同
- Allwmake：项目总编译命令

$\nabla 表示梯度 \ \ \ \ \ \ \ \ \ \nabla· 表示散度 \ \ \ \ \ \\ \nabla^2 表示拉普拉斯算子\ \ 定义为梯度的散度\ \ 等价于\nabla·\nabla$

snappyHexMesh网格划分参数

全局性参数设置主要包含全局网格细化控制参数(castellatedMeshControls)、面贴合参数设置(snapControls)和边界层参数设置(addLayers)。

全局网格细化参数

全局网格细化参数在castellatedMeshControls中设置，其目的为细化背景网格，通过细化背景网格以使几何表面上拥有一定网格量，以提高几何特征捕捉的准确性。同时通过参数设置，保证网格细化时尺寸变化尽量平缓。在castellatedMeshControls中设置具体参数介绍如下：
全局最大网格量maxGlobalCells
网格细化过程中的最大允许网格划分数量。该功能主要目的是保证网格细化过程中，避免划分网格量太大，导致计算机内存溢出。当划分网格量超过此值时，细化过程将立即终止。此时，局部细化功能可能终止运行（例如，未执行某些体域或面域的细化）。
单核最大网格量maxLocalCells
该参数主要应用于网格并行计算，其指定了细化网格过程中每个处理器处理的最大数量网格数。若太小将导致处理器间迭代次数增加，计算效率降低。设置合理的单核最大网格量可极大地提高网格并行计算效率，有助于平衡每个处理器的网格计算量。如果单核处理实际单元数量大于该设定参数，则网格分配算法由平衡细化后单元数控制（默认算法）改为加权平衡细化前单元数控制。固设置该参数时请保证一定的富余量，经常重新平衡每个处理器计算量将减慢网格生成过程。
最大负载平衡参数maxLoadUnbalance
该参数主要应用于网格并行计算。用户可通过设置该值，以允许各个处理器间网格计算负载一定程度上不均衡。当该参数值为0时，即强制负载平衡，即各处理器间处理的网格量严格保持单元总数/计算核数。较低的值（例如0）可能会导致系统频繁的均衡网格负载量。而参数值设置为1时，则完全禁用网格均衡操作。
最小细化单元数minRefinementCells
该参数指定了需细化特征的最小单元数。若特征上网格单元数量小于该参数，则停止对其细化。例如：进行表面细化算法时，软件可能会对小特征面上几个单元网格进行大量细化迭代，占用了较多计算资源，而细化后的网格质量并不理想。用户可以通过该参数，停止其细化迭代。
缓冲层数nCellsBetweenLevels
snappyHexMesh网格拆分采用八叉树法，在网格等级相差较大区域，网格尺寸大小变化比较剧烈。用户可用使用nCellsBetweenLevels参数指定不同细化级别之间的缓冲区体网格层数，使网格大小变化更平缓，该参数值必须大于或等于1。
若用户设置参数值为1，则表示不添加过渡区域。越大的值可使得网格大小过渡越平缓，但将导致网格量增加。
自动检测角resolveFeatureAngle
若用户想自动加密相交面、边以及曲率较大的面、边时，可使用resolveFeatureAngle参数。当曲率变化角超过该参数值时，特征区域网格使用最大面细化等级，而低于此角度的特征均采用最小面细化级别。默认参数值为30，参数值设置为360时，表示关闭此功能。
该参数生效的前置条件：
1、面细化参数中最小和最大细化等级需不同。
2、面贴合过程中特征捕捉需采用隐式方法。
网格域控制点locationInMesh
snappyHexMesh网格划分方法需要用户先提供一套背景网格，然后根据用户导入的封闭几何文件划分网格。在此过程中，用户可通过设置网格域控制点（locationInMesh）参数，指定需要保留背景网格表面与封闭几何表面之间的网格，还是封闭几何内部的网格。保留区域网格中需包含指定的参数点，该点的位置不能和网格单元的面或边重合。
如果该点在STL内部，则对内部网格进行划分，若该点在stl外部且在背景网格内部，则对外部网格进行划分。
面加密
面加密（refinementSurfaces）是针对与几何表面相交的体网格进行加密，以保证后续面贴合的准确性。面加密相关参数设置包括细化等级（Level），最小、最大细化等级（levelMin,levelMax）。并允许用户依据几何表面指定面域（faceZone ），以及依据封闭几何面指定体域（cellZone ）。
体加密
refinementRegions字典对几何区域网格进行体加密，基本参数设置：基本参数包括体区域位置与细化等级参数。
体加密区域位置指定包含三种方式：inside、outside、distance，其中inside为细化几何区域内所有网格，几何区域必须为封闭三维结构；outside为细化几何区域外所有网格，几何区域要求与inside一致；distance为细化几何表面指定范围区域内所有网格。
体加密细化等级levels由两个参数指定。第一位参数为指定细化距离，第二位参数为指定细化等级值。
当用户使用inside与outside方法进行体加密时，只需要设置细化等级参数levels第二位细化等级值，前一位参数只做占位设置（不参与计算）。如下：

refinementRegions  //细化体
   {
     vessel
     {
       mode inside;    //细化几何区域内所有网格
       levels ((1 2));  //细化等级为2
     } 
   }
1
2
3
4
5
6
7
8

若使用distance方法进行体加密，则需同时设置两位参数，且允许用户使用多组细化参数进行体网格加密
1

refinementRegions  //细化体
   {
     vessel
     {
       mode distance;    //细化几何区域内所有网格
       levels (
       (0.5 3) // 在0.5m内细化等级为3
       (1 2) // 在1s内细化等级为2
       );
     } 
   }
1
2
3
4
5
6
7
8
9
10
11

面贴合参数

面贴合参数在snapControls中设置，主要目的是将体网格节点移动到几何表面上，贴合体网格中锯齿状表面。具体参数介绍如下：
捕捉点最大相对距离tolerance
该参数指定贴合算法中捕捉与特征面相关网格节点的最大相对距离，实际捕捉距离为tolerance参数值乘以相邻体网格尺寸。参数值必须大于或等于1，如果值太低，则可能无法使偏差较大的网格节点移动到几何表面上。较高的值有助于增加几何的捕捉范围，但如果参数值设置过高，则有可能捕捉到与表面无关的网格节点。建议值为2-5之间。
网格贴合最大迭代次数nSolveIter
该参数指定了网格贴合算法的最大迭代次数。较高的值会提高网格的质量，网格一致性更好，但网格划分时间会更长。简单模型可以将该参数值设置为100，若贴合后网格质量不太理想，可尝试将该参数值增加到300。
面平滑迭代次数nSmoothPatch
该参数指定了表面上网格贴合的平滑迭代次数。增加迭代次数可以使曲面上网格平滑、贴合性更好，且能降低曲面上网格的歪斜率，但可能导致曲率突变特征（如直角等）弱化。
参数值设置为0，表示保留初始网格外形。建议值为5。
体网格平滑迭代次数nSmoothInternal
在snappyHexMesh网格细化过程中，snappyHexMesh采用八叉树法细化网格。在不同细化等级网格间，软件采用多面体网格过渡。初始的多面体网格将产生30度以上的非正交性。通过使用内部网格平滑处理的迭代，以减小细化过渡区域多面体网格的非正交性。
在执行网格平滑迭代时，边界面网格平滑迭代nSmoothPatch将与内部体网格平滑迭代nSmoothInternal联合使用。平滑迭代顺序为优先执行一次面平滑迭代（nSmoothPatch），再执行一次体网格平滑迭代（nSmoothInterna），以此循环。若用户设置nSmoothInternal参数值大于nSmoothPatch值时，平滑迭代次数统一采用nSmoothPatch参数值。默认值为零，表示禁用体网格平滑迭代。使用此功能时，建议参数值与面平滑迭代（nSmoothPatch）参数值一致。
贴合松弛迭代次数nRelaxIter
该参数指定贴合过程中松弛迭代次数，用以消除质量较差的单元或网格节点。如果迭代完成后网格仍存在质量较差单元，则用户可以尝试增加此迭代次数，较高的值将确保更好的网格质量，但会花费更多计算时间。建议值为5-8之间。
特征边捕捉迭代次数nFeatureSnapIter
该参数指定了特征捕捉迭代次数，以将网格点捕捉到表面边缘。如果在nFeatureSnaplter迭代后局部特征区域网格没有达到足够的质量标准，则取消该区域特征边捕捉并恢复到之前状态。未指定该参数，特征捕捉功能将被禁用。建议参数值为10。
特征捕捉方法(implicitFeatureSnap和explicitFeatureSnap)
在表面贴合步骤中，需保证网格节点捕捉到几何特征。通常表面贴合过程中，点只需沿垂直于表面的方向捕捉特征。但在边缘的位置捕捉方式更复杂，需要更多的迭代次数。SnappyHexMesh提供了两种特征捕捉方法，显示（explicitFeatureSnap）与隐式（implicitFeatureSnap）特征捕捉。用户通过输入true或者false值，来开启或者关闭此功能。
其中显示特征捕捉方法需要用户自定义特征边文件（.eMesh），并且指定特征边的细化等级（通过castellatedMeshControls子字典中features参数指定）。软件根据用户设置的参数对特征边进行细化，以提升用户关注几何特征边的捕捉成功率。
隐式方法不需要用户提取几何特征边，其特征识别自动化程度优于显示特征捕捉方法。它使用全局细化参数中resolveFeatureAngle参数识别曲面几何特征（例如：面的相交线、曲率变化较大的曲面特征）。但在尖角特征或者挡板界面处，显示方法捕捉特征效果优于隐式方法。
多域特征捕捉multiRegionFeatureSnap
该参数用于捕捉多域网格间的特征面，这对于具有多个区域（例如流体区域和固体区域）的网格进行共轭传热模拟或类似操作很重要。该参数生效的前置条件为采用显示特征捕捉方法explicitFeatureSnap。使用该参数时，它会加强特征面两边网格贴合，即内部区域和外部区域，这可能会导致特征面处网格歪斜率上升。用户通过输入参数值true或者false，来开启或者关闭此功能。

边界层参数

snappyHexMesh的网格生成策略是自上而下生成网格，即先生成体网格，再拟合表面上的面网格。边界层网格生成时，软件采用中轴位移法收缩现有体网格。即先沿表面法向向网格划分区域投影指定厚度，再根据投影厚度值计算网格松弛系数收缩现有体网格，收缩后形成的空腔作为边界层网格的划分区域。
snappyHexMesh边界层生成基本参数包含：相对值（relativeSizes）、边界层数（nSurfaceLayers）、膨胀比（expansionRatio）、最后一层厚度（finalLayerThickness）、第一层厚度（firstLayerThickness）边界层总厚度（thickness）、边界层最小总厚度（minThickness）以及nGrow。
用户可通过expansionRatio、finalLayerThickness、firstLayerThickness、thickness四项参数，选择其中两项指定边界层厚度。如果同时指定多个参数，则软件只会使用最后两个参数。因为snappyHexMesh划分边界层时是先挤出一定边界层厚度区域，再插入边界层。为提高边界层网格生成质量，边界层厚度控制参数选择finalLayerThickness优于firstLayerThickness，相对临近单元尺寸比值优于绝对值，即relativeSizes值true优于false。
relativeSizes
边界层基础参数中finalLayerThickness、firstLayerThickness、thickness与minThickness的参数值有两种定义方法:

  1. 采用相对临近单元尺寸比值
  2. 直接由绝对值（单位m）定义。
1
2

用户选用哪种定义方法通过设置relativeSizes确定。
参数值为true：边界层厚度参数值为相对于邻近曲面上的体网格单元大小的比值。
参数值为false：边界层厚度参数值直接由绝对单位的值（单位.米）定义。

边界层膨胀比(expansionRatio)
两个相邻层的厚度比，该值越大，各层间的高度差越大。调整膨胀比参数，不同膨胀比下边界层网格划分结果如下图所示：

边界层最后一层厚度(finalLayerThickness)
确保边界层最后一层网格不大于该值。调整最后一层网格的最大厚度，在不同厚度下边界层网格的划分结果如下(最后一层指的是边界层数中最下面那一层)：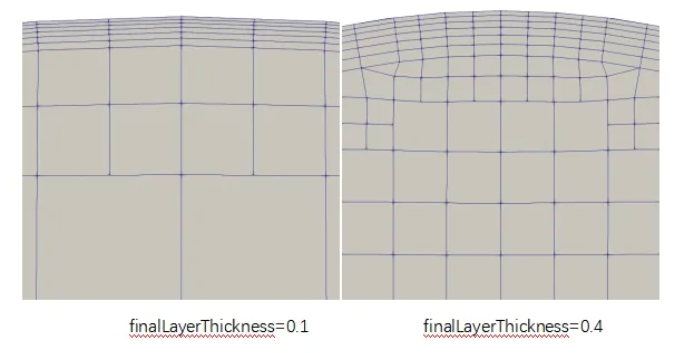

边界层第一层厚度（firstLayerThickness）
指定距离曲面最近的边界层的高度，确保边界层第一层网格不大于该值。调整第一层网格的最大厚度，在不同厚度下边界层网格的划分结果如下：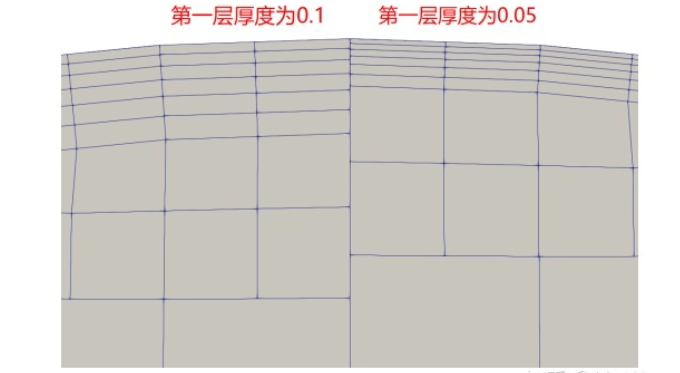

边界层总厚度(thickness)
指定所有边界层的最大厚度。设置较大的边界层总厚度值会导致体网格收缩位移相应增大，体网格变形量增加将导致网格质量降低。当网格质量小于用户设置网格质量控制参数时，系统将取消此处边界层网格划分。

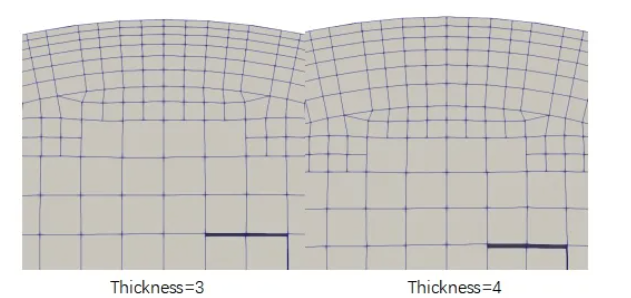
注：边界层总厚度不宜大于5倍相邻体网格尺寸值
最小总厚度（minThickness）
这指定了所有边界层的总体最小厚度。若边界层挤出区域厚度小于该值，则该区域将不会生成边界层。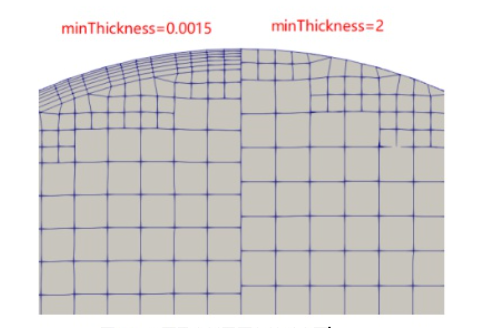

注：此图参数采用相对值，边界层总厚度控制到1，故当minThickness设置为2时，边界层不会生成
最大取消边界层单元数（nGrow）
该参数指定未设置边界层的相邻面相交处边界层的过渡层数。这有助于边界层过渡到特征边附近。
在边界层生成时，体网格需先沿表面法向向网格划分区域收缩指定厚度，有些特征边上存在为移动的节点，则包含该节点的表面单元也不会移动。通过设置nGrow值，指定此单元附近多少个单元不会移动，以保证该特征边附近网格贴体性及质量。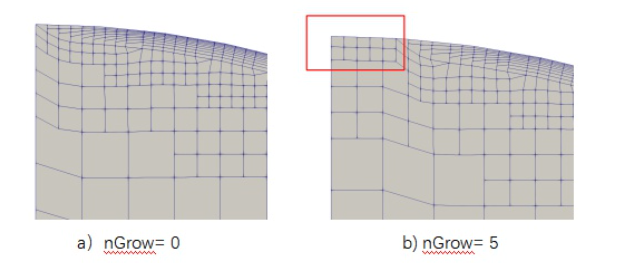

指定面设置边界层基本参数
snappyHexMesh中允许用户对各个表面设置不同的边界层基本参数。如果未指定，则应用全局基本参数。边界层的几何面名称指定与面加密不同，其名称包含几何体与面信息，例如：用户需对几何体box中的Face1面划分边界层，则边界层指定的面名称应该为box_Face1，而不是Face1。并且用户在指定面名称时支持正则表达式。例如：
layers{
box_Face1
{
nSurfaceLayers 3;
}
}
边界层层数(nSurfaceLayers)
nSurfaceLayers该参数确定边界层层数，需在指定面设置边界层基本参数中输入，为强制性参数。
网格划分结果如下：

表面网格最大纵横比(maxFaceThicknessRatio)
该参数指定了表面网格纵横比的最大允许值。当要在高度扭曲的单元上(特别是在角落)生成边界层时，纵横比高于此值的单元上边界层停止生成，以保证边界层网格质量。建议值为0.5
边界层最大面夹角(featureAngle)
两个相邻面边界层网格划分时，软件可根据featureAngle值确定两个面相交边处体网格是否收缩，以确定边界层划分区域。当两个曲面之间的法向夹角 $\theta$ 小于参数featureAngle值时，允许两个曲面的相交边体网格向域内收缩，形成边界层划分区域。用户可根据几何特征设置合适的featureAngle值，以确保边界层的生成范围。
下面显示了特征角为60度和180度时边界层生成的差异。在面夹角为90度区域，若featureAngle值小于面夹角时，则取消夹角处边界层划分。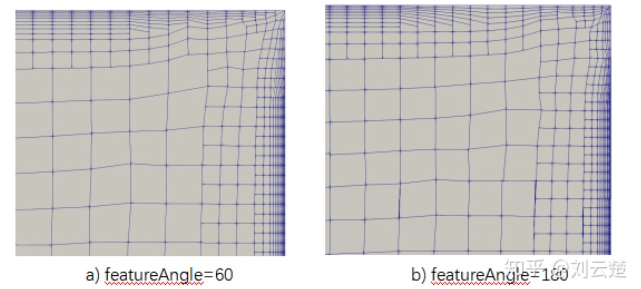

注：为确保角落边缘处边界层生长，featureAngle可设置为180或更高值。但在大角度或扭曲区域边界层质量会急剧下降，受网格质量控制影响，此处边界层也会无法生成。
边界层滑移角度(slipFeatureAngle)
snappyHexMesh在添加边界层时，指定的面边缘的顶点已经固定。当边界层生成到面边缘时，会在此处收缩。若用户想保留在面边缘处的边界层效果，可以指定slipFeatureAngle参数，使边界层面边缘处顶点延边界面滑动，以保证边界层在边缘处的划分空间。例如：当需要划分边界层的面与其相邻面之间的角度大于slipFeatureAngle值时，则保留边界处边界层网格。否则，边界处边界层网格将收缩如下图所示：

注：建议使用70-80之间的最佳值来限制层的滑动，默认值为featureAngle的一半
边界层中终止面的缓冲单元数(nBufferCellsNoExtrude)
为边界层终止端创建缓冲收缩区，即逐渐降低边界层数。设置值小于0，则表示在终止端立即停止边界层。
边界层厚度平滑迭代次数（nSmoothThickness）
边界层网格生成前，软件需要根据投影厚度值收缩现有体网格，用户可通过nSmoothThickness值设置投影厚度值的迭代次数。软件通过迭代投影厚度松弛系数值（1-0）使体网格质量达到质量控制要求。
边界层曲面法线平滑迭代次数（nSmoothSurfaceNormals）
边界层网格生成前，软件需要根据曲面法线方向收缩现有体网格，用户可通过nSmoothSurfaceNormals指定曲面法线平滑迭代次数。该值越高，边界层网格间平滑性越好，但网格划分时间越长。建议值为1。
拾取中间轴点的角度（minMedianAxisAngle）
这指定用于拾取中间轴点的角度。建议值为90度。最新版本90度对应17x版本前的130度。
层厚度与中间轴长度的最大比率（maxThicknessToMedialRatio）
这指定了边界层厚度与中间轴长度的最大比率。当比率大于指定值时，层生长减少。建议值为0.3
体网格收缩迭代次数（nRelaxIter）
单步投影厚度值的迭代中，系统需根据投影厚度值计算体网格收缩松弛系数。用户可设置nRelaxIter参数指定该松弛系数迭代次数，该值越大越有利于提高体网格网格质量。建议值为5
体网格平滑迭代次数（nSmoothNormals）
体网格收缩时，用户可通过nSmoothNormals指定体网格间移动方向的迭代次数。该值越高，体网格间平滑性越好，但网格划分时间越长。建议值为3。
边界层添加的最大总迭代次数（nLayerIter）
这指定了整体边界层添加算法迭代次数。如果达到此迭代次数，边界层网格划分将立即停止，并保留最后一次迭代生成的边界层。建议值为50-60。
宽松质量控制标准的起始迭代次数（nRelaxedIter）
这指定了开始使用宽松网格质量控制的起始迭代次数。软件在划分边界层网格时会优先使用meshQualityControls中基础质量控制参数，检测网格是否满足要求。若边界层添加算法迭代次数达到用户设置nRelaxedIter参数值后，网格依然不能达到质量控制要求，则在此后的迭代中软件将采用用户设置的宽松质量控制标准值。参数建议值为20。

网格质量控制

在SnapPyHexMesh执行全局参数控制、面贴合、局部细化以及边界层生成时，程序都会依据网格质量控制参数不断调整网格迭代。且当网格位移或拓扑更改操作导致单元或面网格质量降低时，软件可根据控制参数撤消移动或拓扑更改操作以将网格还原为之前满足网格质量标准的状态。
网格质量控制参数在子字典meshQualityControl中设置，参数介绍如下：
maxNonOrtho最大非正交角
该参数指定允许的最大非正交角，其通过计算相邻两单元中心点向量与公共面法向量的夹角\theta，此值为0时表示相邻两个网格完全正交。默认参考值为65，当设置为180时，表示关闭此项控制。该参数是衡量网格质量的主要指标之一。
maxBoundarySkewness最大边界面网格偏斜度
此参数指定边界面网格允许的最大偏斜度。其定义一个面或体与理想几何(即等边或等角)的接近程度。默认参考值为20，当设置小于0的值时，表示关闭此项控制。
maxInternalSkewness最大内部面网格偏斜度
参数计算方式与最大边界面网格偏斜度一致，不过其主要测试内部网格质量。默认参考值为4，当设置小于0的值时，表示关闭此项控制。该参数是衡量网格质量的主要指标之一。
maxConcave最大凹度
该参数用于检查构成面的内凹角度，以允许低于该角度的凹面。0表示直面，小于0表示凸面。默认参考值为80，当设置为180时，表示关闭此项控制。
minVol 最小单元体积
该参数为允许最小金字塔单元体积，其为网格绝对体积参数（单位m^3），默认参数为1e-13。设置为较大的负值时，表示禁用此项控制。该参数是衡量网格质量的主要指标之一。
minArea最小网格面面积
该参数为允许最小网格面的面积，默认为-1，该参数设置为负值时，表示禁用此项控制。
minTwist最小面扭曲
使用面中心将面分解为三角形单元，并通过相邻两个单元中心点向量与分解后三角形面法向量的点积计算面扭曲值。默认参考值为0.05，当设置参数小于-1时，表示关闭此项控制。
minDeterminant
该参数指定允许最小归一化单元行列式值。通过计算每一个六面体的雅可比行列式值，然后标准化行列式的矩阵来表征单元的变形。参数值取值范围为0到1，参数值设置为1 表示只允许有理想六面体网格；如果某单元行列式的值为0，则这个立方体有一个或多个退化的边。参数值设置小于或等于0表示允许有负体积单元，默认参数值为0.001。
minFaceWeight
该参数指定允许相邻网格间面权重最小值。其定义了面相对于相邻单元间中心的相对位置（正交时为0.5）。较小的面权重值表示相邻网格尺寸相差较大。参数值取值范围为0到0.5，默认参考值为0.05。
minVolRatio
该参数指定允许相邻网格间的最小体积膨胀率, 参数值取值范围为0到1，默认参考值为0.01。较大的比值会导致插值结果误差较大。
minTriangleTwist
该参数表示允许最小三角单元扭曲值，通过使用面中心将面分解为三角形单元，然后依据相邻的三角形单元法向量的点积计算出三角形面扭曲值。默认参数值为-1，表示禁用此功能。若参数值大于0，则启用此功能项。
minTetQuality
通过网格单元中心和面中心将单元分解为四面体。对于一些跟踪算例时（如流线计算），该参数需要设置为一个较小正值，以确保内部单元质量检查正常运行。默认参数值为1e-30。
nSmoothScale
snappyHexMesh网格划分过程中可将局部网格缩放到之前网格质量满足标准的状态。用户可通过nSmoothScale参数指定每次网格缩放恢复迭代时的平滑次数，参数默认值为4。
errorReduction
errorReduction参数同nSmoothScale参数一样应用于网格缩放恢复迭代，用户可通过该参数减小误差点处的缩放位移量，参数默认值为0.75。
relaxed
软件在划分边界层网格时会优先使用meshQualityControls中基础质量控制参数，检测网格是否满足要求。若边界层添加算法迭代次数达到用户设置nRelaxedIter参数值后，网格依然不能达到质量控制要求，则在此后的迭代中软件将采用用户设置的宽松质量控制标准值，以提高边界层网格的覆盖率。用户可使用relaxed功能对一些关键网格质量控制参数（例如：非正交性nonOrtho、偏斜度skewness等）指定相对宽松的标准。

瞬态模拟和稳态模拟

在OpenFOAM中使用PISO算法以及PIMPLE算法来处理瞬态问题，SIMPLE算法用来处理稳态问题。
求解稳态问题使用simpleFoam求解器进行求解，瞬态可以使用pimpleFoam

离散格式

ddt(时间导数)离散格式：如 default Euler;

Euler(欧拉格式): 瞬态，一阶隐式，保证解的有界性
Crank-Nicolson：瞬态，二阶隐式离散格式，保证解的有界性，有一个系数 $\theta$ 当 $\theta < 1$ ,离散格式是介于Euler和Crank-Nicolson之间的，当 $\theta = 1$ 表示Crank-Nicolson格式，当 $\theta = 0$ 表示Euler格式
backward ：瞬态，二阶隐式，不能保证解的有界性
steadyState: 设置时间导数为0，稳定流动

div(对流项)离散格式：一般不推荐默认离散格式，设置default none;不同的对流项应当手动设置对流项的离散格式

linear ：中心差分格式
upwind：一阶迎风格式
linearUpwind: 二阶迎风格式
QUICK：保证三阶插值精度，但是使用了单点高斯积分，只能够保证二阶准确性，因此如果用了更高阶的离散格式，但还是只能保证二阶准确性
limitedLinear
vanLeer
MUSCL

div(phi,U) Gauss linear(离散格式指定)

在system/fvSchemes内有下面一段程序

divSchemes
{
    default     none;
	div(phi,U)  Gauss linear;
}
1
2
3
4
5

该段程序指定了 $\nabla·$ 的离散方法，其中default none;指的是没有默认的离散格式设置，需要在相应的物理量中明确指定使用哪种离散格式。这样可以确保使用者必须显式地指定离散格式，以避免使用默认设置可能导致的不确定性和错误。div(phi,U) Gauss linear;指定了 $\nabla·(UU)$ 的离散格式为Gauss方法，并使用中心差分方法。
Gauss方法是散度的唯一离散方法，并在其后需要指定所求场的插值格式。指定的方法为：

div()       Gauss <插值格式>;
1

插值格式有如下一下选择(主要的插值格式)：

插值格式	简要说明
中心差分
linear	线性插值(中心差分)
迎风差分
upwind	迎风差分
linearUpwind	线性迎风差分
TVD格式
limitedLinear
vanLeer
NVD格式
SFCD

以上差分格式可以分为两类，一类是通用的(差分格式),第二类是对流项特定的(upwind,TVD,NVD)，后两个目前不常用。如果要制定div(phi,U)为迎风格式，可以写为：

div(phi,U)    Gauss upwind;
1

对流项的差分格式不需要指定通量的插值格式，因为通量(phi)的插值格式已由

interpolationSchemes
{
    default       linear;
}
1
2
3
4

指定。

interpolationSchemes插值格式
interpolationSchemes子字典主要包括从体心到面心的插值项。这些格式的指定需要列出基于某一通量进行插值的这个通量名称。在OpenFOAM应用中，大多数情况为phi，是面标量场(surfaceScalarField)速度通量 $\phi$ 。三个特定对流项的插值格式有三种：一般的，Normalised Variable(NV)和Total Variation Diminishing(TVD)。除了blended格式，一般对流和TVD格式由差分方法和通量的名称来指定，如：基于通量phi的迎风差分定义为缺省格式：

interpolationSchemes
{
	default  upwind  phi;
}
1
2
3
4

某些TVD/NVD格式需要指定系数 $\leq\psi \leq1$ ,当 $\psi=1$ 表示TVD式，可实现较强的收敛性。当 $\psi=0$ 表示实现最好的准确性。推荐设定 $\psi=1$ 。格式基于phi的limitedLinear格式且设定 $\psi=1$ 为缺省插值格式：

interpolationSchemes
{
    default limitedLinear phi 1.0;
}
1
2
3
4

某些标量场需要严格限制有界，OpenFOAM也提供了限制器。要制定某一标量的上下界，插值格式的前面要加上limited并在其后指定上下界。如，指定vanLeer格式严格在[-2,4]有界，方式为：

interpolationSchemes
{
    default limitedVanLeer -2.0 4.0;
}
1
2
3
4

还有一些标量通常在[0,1]有界，也有特殊版本。只需要在插值格式的后面加上01(注意没有空格)。如指定vanLeer格式，并于[0,1]有界：

interpolationSchemes
{
    default vanLeer01;
}
1
2
3
4

OpenFOAM提供了这几个严格有界的格式：limitedLinear,vanLeer,Gamma,limitedCubic,MUSCL和SuperBee。
针对向量场，还可以使用一些增强型的限制器格式，他们将场的方向也考虑进来了。
这些格式后面都加上了V，如limitedLinearV表示增强型的limitedLinear。这些格式提供V版：limitedLinearV,vanLeerV,GammaV,limitedCubicV和SFCDV。

laplacian(rAU,p) linear corrected

在system/fvSchemes里，经常见到

laplacianSchemes
{
    laplacian(rAU,p) Gauss linear corrected;
}
1
2
3
4

laplacianSchemes是在system/fvSchemes文件里的子字典，指定laplacian项的离散格式，其语法是

laplacianSchemes
{
    default           none;
    laplacian(gamma,phi) Gauss <interpolationScheme> <snGradScheme>;
}
1
2
3
4
5

其代表的意义是:
$\nabla·(\Gamma\nabla\phi) = \Gamma\nabla^2\phi=\Gamma(\frac{\partial^2}{\partial x_1^2}\phi+\frac{\partial^2}{\partial x_2^2}\phi+\frac{\partial^2}{\partial x_3^2}\phi)$
FVM方法：
$\nabla·(\Gamma\nabla\phi) = \frac{1}{V}\int_V\nabla·(\Gamma\nabla\phi)dV=\frac{1}{V}\oint_S\Gamma\nabla\phi d\vec{S}=\frac{1}{V}\sum_f(\nabla \phi)_f·\Gamma_f\vec{S_f}$
Laplacian项离散为该控制体所有面的面法向量与该面上 $\phi$ 的梯度的点积之和。从体心到面心需要一种插值方法(interpolationScheme)。
面法向梯度(surface-normal Gradient)指的是在f面上的法向梯度，面上的 $\phi$ 的梯度可由基于控制体的梯度插值求得。
$\nabla_f^\perp\phi=\vec{n}·(\nabla \phi)_f$

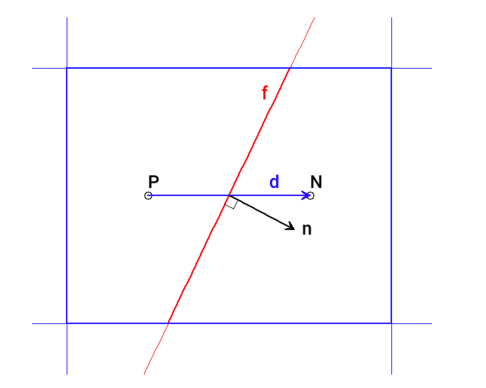
d和n向量的夹角代表了非正交性。
工程分析中的网格划分并不总是正交网格。因此，为保证二阶精度，用隐式正交量加上显式非正交修正的方式，即corrected格式，
$\nabla_f^\perp\phi=\alpha\frac{\phi_P-\phi_N}{|\vec{d}|}+(\vec{n}-\alpha\vec{d})·(\nabla \phi)_f\\ \ \ \ \ \ \ \ \ \ \ \ 隐式部分 \ \ \ \ \ \ \ \ \ \ \ \ \ 显式修正$
式中， $\alpha=\frac{1}{cos(\theta)}$
当非正交角 $\theta$ 增加时，修正量也增加。当 $\theta\to90°$ ，显式修正量可能会很大以致方程的解不稳定。这时，可以在其格式前面增加limited字段，但还需要系数 $\psi\in[0,1]$
$\psi =$

\begin{cases} \begin{array}{ll}% 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \text{不修正，相当于 uncorrected}\\ 0.333 \ \ \ \ \ \ \text{非正交修正} \leqslant 0.5\times 正交量\\ 0.5 \ \ \ \ \ \ \ \ \ \ \text{非正交修正} \leqslant 正交量\\ 1 \ \ \ \ \ \ \ \ \ \ \ \ \ \text{非正交修正,相当于 corrected} \end{array} \end{cases}

$\begin{cases} \begin{array}{ll}% 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \text{不修正，相当于 uncorrected}\\ 0.333 \ \ \ \ \ \ \text{非正交修正} \leqslant 0.5\times 正交量\\ 0.5 \ \ \ \ \ \ \ \ \ \ \text{非正交修正} \leqslant 正交量\\ 1 \ \ \ \ \ \ \ \ \ \ \ \ \ \text{非正交修正,相当于 corrected} \end{array} \end{cases}$

ψ = ⎩ ⎨ ⎧ 0 不修正，相当于 uncorrected 0.333 非正交修正 ⩽ 0.5 \times 正交量 0.5 非正交修正 ⩽ 正交量 1 非正交修正, 相当于 corrected

一般情况下，

\psi

取0.333或0.5，0.333提供较好的稳定性，0.5提供较高的精度。如果

\nabla·(\Gamma\nabla\phi)

需要考虑非正交修正，其离散格式可按一下指定：

laplacianSchemes
{
    default      Gauss linear limited corrected 0.333;
}   
1
2
3
4

wall壁面

patch类型：wall壁面类型，定义速度为fiexedvalue （0 0 0）压力定义为0梯度这种情况下认为真实模拟了一个壁面
血管壁速度设置为noslip，血管变窄处速度有变化
设置为固定值0时，求解的速度场基本相似，没有什么变化。

边界类型：

calculated：该场的值是由其他场的值推导出来的
fixedValue：固定值
zeroGradient：0梯度
inletOutlet：
出口边界条件往外流，
正通量(往外流)：使用的是zeroGradient条件
负通量(内流、回流): 使用的是inletValue固定值

type            inletOutlet;
inletValue      uniform (0 0 0);
value           uniform (0 0 0);
1
2
3

outletInlet：进口边界条件
(负值往场内流，正值往外流)
设置流量边界入口：
volumetricFlowRate是体积流量单位为 $m^3/s$

type    flowRateInletVelocity;
volumetricFlowRate 30;
value $internalField;
1
2
3

离散方程的分离式解法：

SIMPLE算法：

SIMPLE
{
    nNonOrthogonalCorrectors 0;
    pRefCell   0;
    pRefValue  0;
    residualControl
    {
    	p     1e-5;
    	U     1e-5;
    }
}
1
2
3
4
5
6
7
8
9
10
11

其中：

nNonOrthogonalCorrector：表示网格非正交修正循环次数，拉普拉斯项的离散可以引入网格非正交修正，一般情况下，只有在网格非正交性非常明显的时候(非正交角度大于70°)才进行修正，且通常不超过2。（该值会影响最终的求解结果）
pRefCell：表示参考压力位置对应的网格标号，默认为0
pRefValue：表示参考压力值，默认为0
residualControl：表示各求解变量的残差控制，是可选设置，当计算中的残差低于所设定值时，计算将停止，若此处不设定，则计算将持续至设定的迭代次数。

使用GAMG求解物理量的相关设置

p
{
    solver          GAMG;
    smoother        GaussSeidel;
    cacheAgglomeration true;
    nCellsInCoarsestLevel 10;
    mergeLevels      1;
    tolerance       1e-5;
    relTol          0.1;
    agglomerator    faceAreaPair;
}
1
2
3
4
5
6
7
8
9
10
11

其中：

smoother：表示光顺器，即GAMG需要用光顺方式计算残差
cacheAgglomeration：表示团聚是否缓存，如果设置为false，则迭代完成后将团聚成的网格删除以释放内存；如果设置为true，则不会自动删除，在内存充裕的情况下，建议设置为true （设置为false会影响求解结果，收敛速度）
nCellsInCoarsestLevel：表示最粗糙的网格由几个网格构成，数量越多则团聚形成的粗糙网格层越少，相应的低频误差难以准确捕捉而导致收敛速度下降。但是，对于大中型计算(网格数大于100万)，如果实际计算中GAMG的迭代次数较少(即收敛速度较快)，则增大该值可以加快计算速度，则是因为节省了网格团聚所需的时间(粗糙网格层数减少)，此时建议将该值设置为50以上。
aglomerator：表示网格团聚方式，目前提供了dummy与faceAreaPair两种方式，其中dummy是一种虚的团聚方式，仅用于程序测试，并不产生实际的团聚结果，faceAreaPair表示基于网格面权重的团聚方式，将满足一定权重范围的网格进行团聚。
mergeLevels：表示一次生成几层粗糙网格，一般设置为1。对于某些简单的网格，有时候也可以设置为2或者更大。

由于GAMG需要设置光顺器，除上述设置以外，还可以设置nPreSweeps、nPostSweeps以及nFinestSweeps，分别表示在光顺前、光顺后以及对最精细的网格进行光顺时采用的Sweep迭代次数。

icoFoam代码阅读

icoFoam求解的是NS方程，包含时间导数项，对流项，扩散项和压力梯度项，针对层流，不含湍流，针对牛顿流体，不可压缩流动，基于PISO算法的瞬态求解器

寻找头文件命令：
find $WM_PROJECT_DIR -iname 'createTime.H'

//有限体积库头文件的几何
#include "fvCFD.H"
//定义PISO循环  使用PISO循环必备头文件
#include "pisoControl.H"

// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

int main(int argc, char *argv[])
{
    // 根据输入参数argc和argv设置算例根目录rootcase，必备头文件  
    // 检查算例文件夹结构是否完整，不完整报错 主要检查0/U system/controDict等文件是否存在
    #include "setRootCaseLists.H" 
    //创建时间对象，由runTime控制，非定常求解器必备头文件
    #include "createTime.H" 
    //由 $case/constant/polyMesh 创建网格对象 
    #include "createMesh.H"   
    
    // 这个头文件在OpenFOAM大量的求解器中都有涉及，其定义是通量，即为U点乘Sf，为一个标量
    // 包含在createFields.H中
    // #include "createPhi.H" 
     
    //从网格mesh对象构造类pisoControl的对象piso
    pisoControl piso(mesh);
    
    //创建场对象，一般用来指定求解过程中涉及到的物理量
    //例如读取0文件夹下的U p和constant/transportProperties文件下的nu等。
    #include "createFields.H"   
    //初始化连续误差
    #include "initContinuityErrs.H"  
    
    // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
    
    //显示进入时间循环
    Info<< "\nStarting time loop\n" << endl;   
    
    while (runTime.loop())
    {
        //显示当前运行时间
        Info<< "Time = " << runTime.userTimeName() << nl << endl;  
        
        //计算CourantNo，计算库朗数并输出至屏幕
        #include "CourantNo.H"
        
        //求解动量方程
        // Momentum predictor
        
        //构造体积矢量场矩阵  构建方程U
        fvVectorMatrix UEqn
            (
            fvm::ddt(U)
            + fvm::div(phi, U)
            - fvm::laplacian(nu, U)
        );
        
        //momentumPredictor：动量预测求解开关，对于多相流以及低雷诺数一般设置为off；下面求解动量方程
        //即为动量预测的过程，对于瞬态求解器来说，不是必需的。
        //如果进行速度预测（on），则求解完整的动量方程得到预测速度
        //如果不进行速度预测(off），则预测速度直接取当前已知时间步的速度
        if (piso.momentumPredictor())
        {
            solve(UEqn == -fvc::grad(p));
        }
        
        // --- PISO loop
        //nCorrectors：其为 PISO 以及 PIMPLE 调用的关键词，用来设置压力方程以及速度
        //修正方程的迭代步数，一般设置为 2 或者 3；
        // 压力泊松方程的循环
        while (piso.correct())
        {
            //rAU:在速度的最后一个解中，从矩阵中提取对角项并存储其倒数
            //由于对流的非线性，矩阵系数是U的函数
            // rAU相当于1/AD
            // 此处为定义体标量场，定义在体中心 1/Ap,其在压力修正步中保持不变
            volScalarField rAU(1.0/UEqn.A());  
            
            // UEqn.H()是UEqn减去非对角项和U的乘积
            // 定义在体中心
            // HbyA相当于 AH/AD
            // 定义HbyA，可知HbyA = rAU*UEqn.H
            volVectorField HbyA(constrainHbyA(rAU*UEqn.H(), U, p)); 
            // Ap虽然在修正步内不变，但是HbyA是会更新的
            // UEqn.A() 对应的是Ap在当前时间内迭代中其为不变的，在进入下一个时间步更新
            
            //组建phiHbyA，将上述体积矢量场转化为面心标量场  定义在面上
            //fvc::interpolate(rAU)*fvc::ddtCorr(U, phi)的作用是保证速度通量的全局守恒，以确保压力方程有解
            //fvc::flux(HbyA) 表示方程13的第一项
            surfaceScalarField phiHbyA
                (
                "phiHbyA",
                fvc::flux(HbyA)
                + fvc::interpolate(rAU)*fvc::ddtCorr(U, phi)
            );
            //理论推导中，phiHbyA=fvc::flux(HbyA)=HbyA*Sf，
            //但是由于离散会存在误差，为了进一步减小这个误差，在这个后面加了一个修正项。
            //fvc::interpolate(rAU)*fvc::ddtCorr(U, phi)为修正项
            //HbyA 是插值到面上的值
            
            // 修正压力边界（梯度为0）上的 phiHbyA，使其满足连续性方程,调整边界值，保证速度边界条件守恒
            //adjustphi()是用于对压力全部为Neumann边界条件的情况下，
            //给定一个附加条件使得压力有解，这个附加条件通过adjustphi()进行。
            adjustPhi(phiHbyA, U, p);
            
            // Update the pressure BCs to ensure flux consistency
            //更正压力边界条件，保证通量守恒
            constrainPressure(p, U, phiHbyA, rAU);
            
            // Non-orthogonal pressure corrector loop
            // 网格非正交压力修正循环
            // nNonOrthogonalCorrectors：所有的算法均需要指定这个参数，
            // 其用于更新压力方程中显性非正交修正项∇⋅((1/ )∇p)的求解次数，一般设置为 0（稳态）或 1；
            while (piso.correctNonOrthogonal())
            {
                // Pressure corrector
                // 构造压力方程进行求解
                fvScalarMatrix pEqn
                    (
                    fvm::laplacian(rAU, p) == fvc::div(phiHbyA)
                );
                
                pEqn.setReference(pRefCell, pRefValue);
                
                pEqn.solve();
                
                if (piso.finalNonOrthogonalIter())
                {
                    // 在最后一次非正交校正中，使用最新压力校正通量
                    phi = phiHbyA - pEqn.flux();
                }
            }
            
            // 计算连续方程误差
            #include "continuityErrs.H"
            
            U = HbyA - rAU*fvc::grad(p);  //构建速度场
            // 校正速度，满足边界条件
            U.correctBoundaryConditions();
        }
        ·
            //输出计算结果，写入时间文件夹
            runTime.write();
        
        // 显示求解器执行时间以及CPU耗时
        Info<< "ExecutionTime = " << runTime.elapsedCpuTime() << " s"
            << "  ClockTime = " << runTime.elapsedClockTime() << " s"
            << nl << endl;
    }
    
    // 结束
    Info<< "End\n" << endl;
    
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153

icoFOAM中的PISO算法来耦合速度场和压力场

icoFoam求解的方程，NS方程如下：
$\nabla·u=0 \\ \frac{\partial u}{\partial t}+\nabla·uu-\nabla·[\nu(\nabla u)]=-\nabla p$
连续性方程：速度场散度为0
动量守恒方程：包含时间导数项，对流项，扩散项，压力梯度项

求解难点：

对流项为非线性方程
压力速度耦合

假设PISO算法在足够的小时间步长下：

压力速度耦合是强于非线性耦合
对对流项进行线性化：

$\nabla·uu= \nabla·u_0u_n$
对流相中第一个u为已知量，为前一个时间步的u，第二个u为未知量，需要通过求解NS方程求得。

对速度场进行显式修正，对速度场进行修正的过程中，只有压力场对它有影响

PISO算法的两大步骤：

求解动量方程
压力修正

在icoFoam中对其进行压力修正的代码：

//定义标量场rAU 定义在体中心
//UEqn.A()代表A_D   rAU = 1/A_D
volScalarField rAU(1.0/UEqn.A());

//定义矢量场HbyA 定义在体中心
//UEqn.H()代表A_H   HbyA = A_H/A_D 
volVectorField HbyA("HbyA", U);
HbyA = rAU*UEqn.H();

//组建phiHbyA，将上述体积矢量场转化为面心标量场  定义在面上
//fvc::interpolate(rAU)*fvc::ddtCorr(U, phi)的作用是保证速度通量的全局守恒，以确保压力方程有解
//fvc::flux(HbyA) 表示方程13的第一项
//phiHbyA 整体就相当于方程13的第一项
surfaceScalarField phiHbyA
(
    "phiHbyA",
    fvc::flux(HbyA)
    + fvc::interpolate(rAU)*fvc::ddtCorr(U, phi)
);


//方程19为压力修正所导致的通量变化
// Pressure corrector
// 构造压力方程进行求解  方程17
fvScalarMatrix pEqn
(
  fvm::laplacian(rAU, p) == fvc::div(phiHbyA)
);

pEqn.setReference(pRefCell, pRefValue);

pEqn.solve();

if (piso.finalNonOrthogonalIter())
{
    // 在最后一次非正交校正中，使用最新压力校正通量
    // pEqn.flux()为方程19
    phi = phiHbyA - pEqn.flux();
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

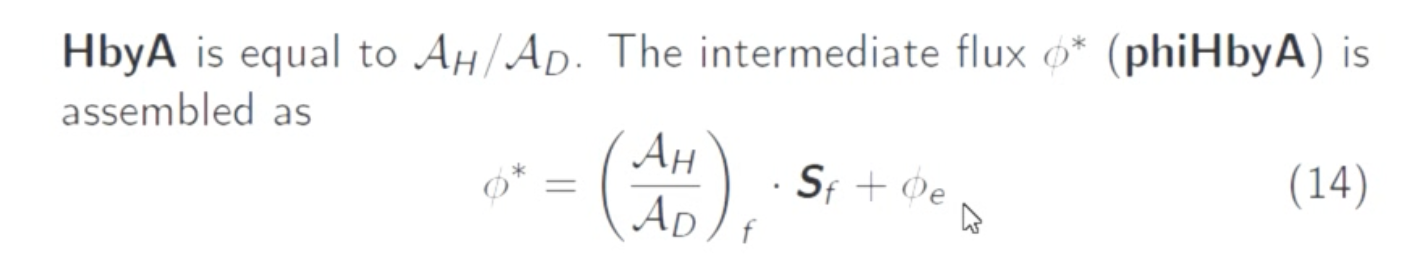
压力修正要点：OpenFOAM中主要未知量为通量，而非速度，我们所要满足连续性方程的是通量场而非速度场。

多态

动态多态的设计思想：对于相关的对象类型，确定它们之间的一个共同功能集，然后在基类中，把这些共同的功能声明为多个公共的虚函数接口。各个子类重写这些虚函数，以完成具体的功能。客户端的代码（操作函数）通过指向基类的引用或指针来操作这些对象，对虚函数的调用会自动绑定到实际提供的子类对象上去。

静态多态的设计思想：对于相关的对象类型，直接实现它们各自的定义，不需要共有基类，甚至可以没有任何关系。只需要各个具体类的实现中要求相同的接口声明，这里的接口称之为隐式接口。客户端把操作这些对象的函数定义为模板，当需要操作什么类型的对象时，直接对模板指定该类型实参即可（或通过实参演绎获得）。

OpenFOAM代码语句与公式对应关系

$\nabla·u=0 \\ \frac{\partial u}{\partial t}+\nabla·uu-\nabla·[\nu(\nabla u)]=-\nabla p$

fvm::ddt(U)

返回fvVectorMatrix，返回N*N的矩阵，矩阵中每个元素都是括号内的U，因此是Vector

与动量方程对应关系: $\frac{\partial U}{\partial t}$
与离散方程对应关系： $\frac{\partial}{\partial t}\int_{V_p}UdV\approx\frac{\partial}{\partial t}(U_P V_P)=a·U_P^{n+1}+bU_P^{n}$

最后一个等号所得的形式取决于定义在fvSchemes中的ddtSchemes离散格式

fvm::div(phi,U)

返回fvVectorMatrix

与动量方程对应关系： $\nabla·(UU)$
与离散方程对应关系： $\int_{V_P}\nabla·(UU)dV = \int_{\partial V_P}(UU)dS \approx\sum(UU)_fS\approx\sum F_f^nU_f^{n+1}=a·U_P^{n+1}+\sum b_NU_N^{n+1}$

因此div(a,b)操作对应的运算符为 $\nabla·(ab)$ ，对应的离散为 $\sum ab$

fvm::laplacian(nu,U)

返回fvVectorMatrix

与动量方程对应关系： $\nabla·(\nu\nabla u)$
与离散方程对应关系： $\int_{V_P}\nabla·(\nu\nabla U)dV=\int_{\partial V_P}(\nu\nabla U)dS\approx\sum\nu(\nabla U^{n+1})_fS=\sum\nu[(\nabla U^{n+1})_f·\frac{S}{S_f}]S_f=a·U_P^{n+1}+\sum b_NU_N^{n+1}$

其中 $n=\frac{S}{S_f}$ 为单位矢量， $S_f$ 为标量，值为面积，上式第四项对应代码fvm::snGrad(U).
上式第四项到第五项的过渡取决于面上梯度 $(\nabla U)_f$ 的离散方式，即如何将面上梯度转化为体心值，定义在fvSchemes/laplacianSchemes

fvc::grad§

返回scalarField，该返回类型为fvVectorMatrix的子集，执行 $so l v e (U Eq n == - f v c :: g r a d (p))$ 时将后者做了类型强制转换。

与动量方程对应关系： $\nabla p$
与离散方程对应关系： $\int_{V_P}\nabla pdV=\int_{\partial V_P}pdS \approx\sum p_f^nS=p_P^n+\sum p_N^n$

fvSchemes/gradSchemes决定了如何由面上值 $p_f$ 插值得到体心值 $p_P$

solve(UEqn == -fvc::grad§)

求解括号内以fvMatrix作为系数矩阵的AX=B，很显然A为UEqn，双等号右边为B，两者相等解出X，即U。另外，该语句没有返回值，但是会将所求解的场量更新，即更新U

fvc::flux(HbyA)

返回surfaceScalarField,其大小为内部面的个数，等于constant/polyMesh/neighbour文件中元素的个数。HbyA为volVectorField，其大小为网格数，可见该操作是将体心矢量场转变为面心标量场，由矢量场转成标量场，将该矢量做了点乘操作。
$flux[(HbyA)_P] = (HbyA)_f·S$
上述过程涉及将体心值插值为面心值。

fvc::div(phiHbyA)

其返回值类型为scalarField，该代码对应的离散过程如下：
$\sum(HbyA)_f·S$

fvm::laplacian(rAU,p)

fvm的返回值类型为fvMatrix，具体为标量还是矢量取决于拉普拉斯项中的未知数类型。该代码对应的过程为
$\int_{V_P}\nabla·(\frac{1}{A}\nabla p)dV=\int_{\partial V_P}(\frac{1}{A}\nabla p)dS\approx\sum(\frac{1}{A}\nabla p^{n+1})_fS=\sum[(\frac{1}{A}\nabla p^{n+1})_f·\frac{S}{S_f}]S_f=a·p_P^{n+1}+\sum b_Np_N^{n+1}$

非正交修正

非正交修正(Non-Orthogonal Correctioin,简称NOC)是一种用于有限体积法中处理非正交网格的技术。在非正交网格中，相邻网格单元之间的边界不再垂直或平行，导致离散算子的精度受到影响，从而可能引起数值解的误差和不稳定性。
NOC的基本思想是对离散算子进行修正，以考虑非正交网格的影响。具体来说，NOC通过添加额外的修正项来纠正离散算子中漏掉的跨边界通量，并考虑到非正交角的影响。这些修正项可以根据网格单元之间的夹角、面积等几何特征进行计算。
NOC技术的优点在于它可以显著提高有限体积法在非正交网格上的精度和稳定性，并且与其他技术(如梯度重构、限制器等)可以结合使用。但它也存在一些缺点，比如增加了计算量和程序复杂度，可能会导致数值解的非物理震荡等问题。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/Li_阴宅/article/detail/801370