此主要讨论图像处理与分析。虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来，但鉴于它们与计算机视觉的紧密联系，以 及它们的出处，没有把它们纳入到图像处理与分析中来。同样，这里面也有一些 也可以划归到计算机视觉中去。这都不重要，只要知道有这么个方法，能为自己 所用，或者从中得到灵感，这就够了。
注意：Registration可翻译为“配准”或“匹配”，一般是图像配准，特征匹配(特征点匹配)。
15. Image Registration
图像配准最早的应用在医学图像上，在图像融合之前需要对图像进行配准。在现在的计算机视觉中，配准也是一个需要理解的概念，比如跟踪，拼接等。在KLT中，也会涉及到配准。这里主要是综述文献。
[1998 MIA] Image matching as a diffusion process
[1992 PAMI] A Method for Registration of 3-D shapes
[1992] a survey of image registration techniques
[1996 MIA] Multi-modal volume registration by maximization of mutual information
[1997 IJCV] Alignment by Maximization of Mutual Information
[1998 MIA] A survey of medical image registration
[2003 IVC] Image registration methods a survey
[2003 TMI] Mutual-Information-Based Registration of Medical Survey
[2011 TIP] Hairis registration
翻译
图像配准方法调查——
作者：Barbara Zitova, Jan Flusser
摘要 -本文旨在介绍最近以及经典的图像配准方法。图像配准是叠加在不同时间，从不同视点和/或通过不同传感器拍摄的同一场景的图像(两个或多个)的过程。配准在几何上对齐两个图像(参考图像和感应图像)。所审查的方法根据其性质(基于区域和基于特征)以及图像配准过程的四个基本步骤进行分类：特征检测，特征匹配，映射功能设计以及图像变换和重采样。本文提到了该方法的主要贡献，优点和缺点。还讨论了图像配准和前景展望方面的问题。本文的主要目的是为涉及图像配准的研究人员提供全面的参考资料，无论特定的应用场合如何。2003 Elsevier B.V.保留所有权利。
关键字：图像配准；特征检测；特征匹配；映射功能；重采样
1.简介
图像配准是叠加从不同视点和/或由不同传感器在不同时间拍摄的同一场景的两个或多个图像的过程。它在几何上对齐两个图像，即参考图像和感应图像。由于不同的成像条件而引入了图像之间的当前差异。图像配准是所有图像分析任务中的关键步骤，在这些任务中，最终信息是从各种数据源(如图像融合，变更检测和多通道图像恢复)的组合中获得的。通常，在医学(结合计算机断层扫描(CT))中，遥感(多光谱分类，环境监测，变化检测，图像拼接，天气预报，创建超分辨率图像，将信息集成到地理信息系统(GIS)中)需要配准。和NMR数据以获取有关患者的更完整信息，监视肿瘤生长，治疗验证，将患者数据与解剖图谱进行比较)，制图(地图更新)和计算机视觉(目标定位，自动质量控制)，仅举几例。
在过去的几十年中，图像采集设备经历了快速的发展，并且获得的图像的数量和多样性不断增加，从而引发了对自动图像配准的研究。Brown于1992年对图像配准方法进行了全面调查[26]。本文的目的是涵盖稍后介绍的相关方法，并以此方式映射配准技术的当前发展。根据科学信息研究所(ISI)的数据库，在过去十年中，有关图像配准的主题发表了1000多篇论文。为了保持连续性并提供图像配准研究的完整视图，还包括1992年之前发布的成为经典或引入关键思想的方法，这些方法仍在使用中。我们不打算讨论特定算法的细节或描述结果。比较实验，我们想总结主要方法并指出配准方法的有趣部分。
在第2节中，将讨论图像配准的各个方面和问题。第3节介绍了基于区域的方法和基于特征的方法。第4节介绍了用于特征匹配的现有算法。映射函数设计的方法在第5节中给出。最后，第6节概述了图像转换和重采样的主要技术。图像配准精度的评估在第7节中介绍。第8节总结了配准方法研究的主要趋势，并展望了未来。
2.图像配准方法
如上所述，图像配准已广泛用于遥感，医学成像，计算机视觉等。根据图像采集的方式，通常将其应用分为四个主要组：
不同的视点(多视点分析) 。从不同的视角获取同一场景的图像。目的是获得扫描场景的更大的2D视图或3D表示。
应用示例：遥感-对被调查区域的图像进行马赛克处理。计算机视觉—形状恢复(从立体形状恢复)。
不同时间(多时相分析)。同一场景的图像通常是在不同时间(可能有规律地)在不同时间获取的。目的是发现并评估在连续图像采集之间出现的场景变化。
应用示例：遥感-监控全球土地使用情况，景观规划。计算机视觉-自动更改检测，用于安全监控，运动跟踪。医学成像-监测治疗效果，监测肿瘤进展。
不同的传感器(多模式分析)。同一场景的图像由不同的传感器获取。目的是整合从不同源流获得的信息，以获得更复杂和详细的场景表示。
应用示例：遥感-融合来自具有不同特征的传感器的信息，例如全色图像，提供更好的空间分辨率，具有更好的光谱分辨率的彩色/多光谱图像或与云层和太阳照度无关的雷达图像。医学成像-结合记录人体解剖结构(如磁共振图像(MRI)，超声或CT)的传感器与监测功能和代谢性人体活动的传感器(如正电子发射断层扫描(PET)，单光子发射计算机断层扫描(SPECT)或磁共振波谱)的组合(太太)。结果可以应用于例如放射治疗和核医学。
场景到模型配准。记录场景的图像和场景的模型。该模型可以是场景的计算机表示，例如GIS中的地图或数字高程模型(DEM)，具有相似内容的另一个场景(另一个患者)，“平均”样本等。目的是将获取的图像定位在场景/模型和/或进行比较。
应用示例：遥感-将航空或卫星数据配准到地图或其他GIS层中。计算机视觉-目标模板与实时图像匹配，自动质量检查。医学成像-将患者的图像与数字解剖图谱，标本分类进行比较。
由于要配准的图像的多样性以及各种类型的劣化，因此无法设计适用于所有配准任务的通用方法。每种方法不仅应考虑图像之间几何变形的假定类型，还应考虑辐射变形和噪声破坏，所需的套准精度以及与应用相关的数据特征。
尽管如此，大多数配准方法还是由以下四个步骤组成(见图1)：
图1.图像配准的四个步骤：第一行-特征检测(在这种情况下，将角用作特征)。 中间行-通过不变描述符进行功能匹配(相应的对用数字标记)。 左下方-利用已建立的对应关系进行变换模型估计。 右下角-使用适当的插值技术进行图像重采样和变换。
†特征检测。突出的和独特的对象(边界边界区域，边缘，轮廓，直线相交，角等)是手动或最好自动检测的。为了进行进一步处理，这些特征可以用它们的点代表(重心，线尾，独特点)表示，在文献中称为控制点(CP)。
†功能匹配。在该步骤中，建立在感测图像中检测到的特征与参考图像中检测到的特征之间的对应关系。
为此，使用了各种特征描述符和相似性度量以及特征之间的空间关系。
†变换模型估计。估计将感测的图像与参考图像对准的所谓的映射函数的类型和参数。映射函数的参数通过已建立的特征对应关系进行计算。
†图像重采样和变换。所感测的图像借助于映射功能被变换。非整数坐标中的图像值通过适当的插值技术计算。
每个配准步骤的实施都有其典型的问题。首先，我们必须决定哪种功能适合给定的任务。这些特征应该是与众不同的对象，它们经常散布在图像上并且易于检测。通常，需要特征的物理可解释性。
在参考图像和感应图像中检测到的特征集必须具有足够的公共元素，即使在图像未完全覆盖相同场景或存在物体遮挡或其他意外更改的情况下也是如此。检测方法应具有良好的定位精度，并且对假定的图像质量不敏感。在理想情况下，该算法应该能够在场景的所有投影中检测到相同的特征，而不管特定的图像变形如何。
在特征匹配步骤中，可能会出现由错误的特征检测或图像质量下降引起的问题。由于不同的成像条件和/或由于传感器的光谱灵敏度不同，因此物理上对应的特征可能会有所不同。特征描述和相似性度量的选择必须考虑这些因素。特征描述符应该与假定的降级无关。同时，它们必须具有足够的可分辨性，以便能够在不同的特征之间进行区分，并且必须足够稳定，以免受到轻微的意外特征变化和噪声的影响。在不变空间内的匹配算法应该是鲁棒且有效的。在另一张图片中没有相应对应内容的单个功能不应影响其性能。
映射函数的类型应根据有关采集过程和预期图像质量的先验信息进行选择。如果没有先验信息可用，则该模型应具有足够的灵活性和通用性，以处理可能出现的所有可能的降级。还需要考虑特征检测方法的准确性，特征对应估计的可靠性以及可接受的近似误差。而且，必须做出关于必须通过配准去除图像之间的哪些差异的决定。如果目标是检测变更，则最好不要删除我们正在寻找的差异。这个问题非常重要，也非常困难。
最后，适当类型的重采样技术的选择取决于所需的插值精度与计算复杂度之间的权衡。在大多数情况下，最近邻或双线性插值已足够。但是，某些应用程序需要更精确的方法。
由于其在各种应用领域中的重要性以及其复杂的性质，图像配准已成为许多近期研究的主题。历史上第一篇调查论文[64]主要涵盖了基于图像相关性的方法。参考文献[26]也许是对通用图像配准方法的最详尽的综述。参考文献[86,111,123,195]总结了特别应用于医学成像的配准技术。参考文献[9]综述了医学成像中基于表面的配准方法。基于卷的配准在参考文献[40]中进行了审查。在[59，81,106]中描述和评估了主要应用于遥感的配准方法。范德比尔特大学开展了各种配准方法的大型评估项目[206]。
可以根据各种标准对配准方法进行分类。通常使用的是应用领域，数据维数，假定图像变形的类型和复杂性，计算成本以及配准算法的基本思想。在这里，考虑到将配准分解为所描述的四个步骤，根据基本思想选择分类。根据其主要贡献涵盖了超出此四步框架的技术。
3.特征检测
以前，要素是由专家手动选择的对象。在此配准步骤的自动化过程中，形成了两种主要的特征理解方法。
3.1 基于区域的方法
基于区域的方法将重点放在特征匹配步骤上，而不是其检测上。在这些方法中未检测到任何特征，因此省略了图像配准的第一步。属于该类的方法将在与其他配准步骤相对应的部分中进行介绍。
3.2 基于特征的方法
第二种方法是基于图像中的显着结构(特征)的提取。重要区域(森林，湖泊，田野)，线(区域边界，海岸线，道路，河流)或点(区域角，线相交，曲线上的点具有高曲率)在此处被理解为特征。它们应该是不同的，分布在整个图像上，并且在两个图像中都可以有效地检测到。在整个实验过程中，它们会及时稳定在固定位置。
通过特征检测器的不变性和准确性以及通过重叠准则来确保在感测图像和参考图像中特征集的可比性。换句话说，无论图像几何形状，辐射条件，附加噪声的存在以及所扫描场景的变化如何，所检测到的特征集的公共元素的数量应足够高。这些功能的定义暗示了这些功能的“卓越性”。与基于区域的方法相比，基于特征的方法不适用于图像强度值。这些功能代表更高级别的信息。此属性使基于特征的方法适用于预期照明变化或需要多传感器分析的情况。
区域特征。类似区域的特征可以是适当大小的一般高对比度封闭边界区域[54,72]，水库和湖泊[71,88]，建筑物[92]，森林[165]，城市区域的投影[161]或阴影[24]。封闭边界区域的一般标准是普遍的。这些区域通常由其重心表示，这些重心在旋转，缩放和倾斜方面是不变的，并且在随机噪声和灰度级变化下保持稳定。
区域特征通过分割方法来检测[137]。分割的准确性会显着影响所得配准。 Goshtasby等人[72]提出了细分流程的改进措施，以提高配准质量。图像的分割是与配准一起反复进行的；在每次迭代中，使用对象对应关系的粗略估计来调整分割参数。他们声称可以实现亚像素配准的准确性。
近来，关于尺度变化不变的区域特征的选择引起了关注。 Alhichri和Kamel [2]使用距离变换提出了虚拟圆的想法。仿射不变邻域在[194]中进行了描述，基于哈里斯拐角检测器[135]和经过检测到的拐角的边缘(弯曲或笔直)。 Matas等人[127]提出了一种基于图像强度均匀性的使用最大稳定极值区域的方法。
线特征。线特征可以是医学成像中一般线段[92,132,205]，对象轮廓[36、74,112]，沿海线[124,168]，道路[114]或细长解剖结构[202]的表示。线对应关系通常用线末端或中点对表示。
标准的边缘检测方法，如Canny检测器[28]或基于高斯拉普拉斯算子的检测器[126]，都用于线特征检测。在[222]中可以找到对现有边缘检测方法及其评估的调查。李等。[112]提出利用在参考图像(光学数据)中已经检测到的特征来检测感测图像(具有斑点噪声的SAR图像，这是在这种类型的数据中存在的典型劣化)中的线的检测。他们应用了弹性轮廓提取。 Maintz等人[121,122]提出了对多峰医学图像中特征边缘检测和脊检测的不同算子的比较。
点要素。点要素组包括以下方法：线交点[175,198]，道路交叉口[79,161]，水区域的质心，油气垫[190]，高方差点[45]，使用Gabor小波检测到的局部曲率不连续性[ 125、219]，曲线[3,11]的拐点，小波变换的局部极值[58,90]，相对于指定的相似度度量[115]以及角[20,92,204]最有特色的点。
在大多数情况下，特征检测器的核心算法遵循“点”的定义，即线相交，闭合边界区域的质心或小波变换的局部模量最大值。拐角形成特定的特征类别，因为很难用数学方法定义“成为拐角”属性(直觉上，拐角被理解为区域边界上的高曲率点)。在开发精确，鲁棒和快速的拐角检测方法上已经花费了很多精力。在参考文献[155,172,220]中可以找到对拐角检测器的调查，在参考文献[156]中可以找到最新，最详尽的信息。后者还分析探测器的定位特性。角点被广泛用作CP，主要是因为它们对成像几何形状的不变性以及因为它们被人类观察者很好地感知。
Kitchen and Rosenfeld [101]提出将图像函数的二阶偏导数用于角点检测。 Dreschler和Nagel [43]搜索了高斯曲率的局部极值。然而，基于图像函数的二阶导数的角检测器对噪声敏感。因此，Forstner [62]开发了一种更健壮但耗时的拐角检测器，它仅基于一阶导数。著名的哈里斯探测器(也称为普莱西探测器)[135]实际上是其倒数。参考文献[107]中描述了Forstner检测器的应用，该检测器用于牙种植体图像的配准。
Smith和Brady [173]在他们强大的SUSAN方法中选择了更直观的方法。作为标准，他们使用与中央像素相同颜色的区域大小。 Trajkovic和Hedley [192]使用这样的想法设计了他们的算子，即在各个方向上拐角处的图像强度变化应该很大。
最近，Zitova´等人[224]提出了一种不使用任何导数的参数拐角检测器，其设计用于处理模糊和嘈杂的数据。 Rohr等。设计的拐角检测器，甚至用于3D数据，也允许用户交互[158]。
检测点的数量可能非常高，这增加了配准所需的计算时间。几位作者提出了一种有效选择点子集(优于随机点)的方法，该方法不会降低所得配准的质量。 Goshtasby [71]仅使用了属于整个集合的凸包的点。 Lavine [104]提出使用构成集合的最小生成树的点。埃勒斯[45]将点合并为“团块”，即密集的大型团簇。
3.3 摘要
总而言之，如果图像包含足够鲜明且易于检测的对象，则建议使用基于特征的方法。通常是在遥感和计算机视觉中的应用情况。典型的图像包含很多细节(城镇，河流，道路，森林，房间设施等)。另一方面，医学图像的细节不是那么丰富，因此这里通常采用基于区域的方法。有时，可以通过专家进行交互式选择或通过引入相对于患者严格定位的外部特征(皮肤标记，螺丝标记，牙科适配器等)来解决医学图像中缺乏独特对象的问题[123]。参考文献中分析了基于区域和基于特征的方法对具有各种对比度和清晰度的图像的适用性。 [151]。最近，同时使用基于区域和基于特征的方法的配准方法开始出现[85]。
4.特征匹配
参考图像和感测图像中的检测到的特征可以通过它们附近的图像强度值，特征空间分布或特征符号描述进行匹配。一些方法在寻找特征对应时，同时估计映射函数的参数，从而合并第二和第三配准步骤。
在以下段落中，将保留两个主要类别(分别是基于区域的方法和基于特征的方法)，并根据匹配方法的基本思想将其进一步分类为子类别。
4.1 基于区域的方法
基于区域的方法，有时也称为类似关联的方法或模板匹配[59]，将特征检测步骤与匹配部分合并在一起。这些方法处理图像时不会尝试检测突出的对象。在第二配准步骤[4,12,145]中，将预定义大小的窗口甚至整个图像用于对应估计。
基于区域的方法的局限性在于其基本思想。首先，最常使用的矩形窗口适合于仅通过平移而局部不同的图像配准。如果图像因更复杂的变换而变形，则这种类型的窗口将无法覆盖参考图像和感应图像中的场景相同部分(矩形可以转换为其他形状)。几位作者提出将圆形的窗口用于相互旋转的图像。但是，如果在图像之间存在更复杂的几何变形(相似性，透视变换等)，也会破坏这种简单形状的窗口的可比性。
基于区域的方法的另一个缺点是窗口内容的“显着性”。由于没有显着性，包含平滑区域但没有任何突出细节的窗口很可能会与参考图像中的其他平滑区域不正确地匹配。应当优选在图像的独特部分中检测出配准特征。 Windows的选择通常不是基于其内容评估的，因此可能没有此属性。
经典的基于面积的方法(例如互相关(CC))可直接匹配图像强度，而无需进行任何结构分析。因此，它们对强度变化敏感，例如，噪声，变化的照明和/或使用不同的传感器类型会引起强度变化。
4.1.1 类相关方法
基于面积的方法的经典代表是归一化的CC及其修改[146]。
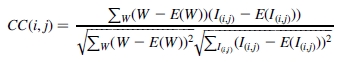
从感测到的参考图像为窗口对计算相似度，并搜索其最大值。将达到最大值的窗口对设置为对应的窗口对(参见图2)。如果需要配准的子像素精度，则需要使用CC测量值的插值。尽管基于CC的配准只能精确对齐相互翻译的图像，但是当出现轻微旋转和缩放时，也可以成功应用。
图2.基于区域的匹配方法：使用归一化互相关(中间行)和相位相关(底部行)将小模板配准到整个图像。 最大值标识匹配位置。 该模板具有与参考图像相同的光谱带(左侧的图表示红色通道匹配)，具有不同的光谱带(右侧的图显示红色-蓝色通道匹配)。 通常，在多模态数据的情况下，归一化互相关可能会失败。
CC的通用版本适用于几何形状更变形的图像。他们为检测到的图像窗口的每个假定的几何变换计算CC [83]，并且比平移(通常是相似变换)能够处理更复杂的几何变形。 Berthilsson [17]试图以这种方式记录甚至是仿射变形的图像，Simper [170]提出使用分治系统和CC技术来记录因透视图变化以及镜头缺陷而变化的图像。但是，随着转换复杂度的增加，计算负荷会快速增长。如果要配准的图像/对象被部分遮挡，则可以应用基于增量符号相关性的扩展CC方法[98] [99]。
类似于CC方法的是顺序相似度检测算法(SSDA)[12]。与CC相比，它使用顺序搜索方法和计算上更简单的距离度量。它累加图像强度值的绝对差之和(矩阵L1范数)并应用阈值标准-如果累加的总和超过给定阈值，则来自参考图像和感测图像的候选窗口对将被拒绝，下一对是经过测试。该方法可能不如CC准确，但速度更快。参考文献[211]使用了平方差相似度总和。使用分段仿射估计来分解分解为小块的图像，从而对透视变形进行迭代估计。
近来，在多模式配准领域已经引起了对基于相关比率的方法的极大兴趣。与经典CC相反，这种相似性度量可以处理由于使用不同传感器(多模式图像)而导致的图像之间的强度差异。它假定强度依赖性可以由某些函数表示。参考文献[154]发现了该方法与针对多峰数据开发的其他几种算法的比较。在具有某些特征的噪声图像(固定模式噪声)的情况下，基于投影的配准[27]分别处理累积的图像行和列，其性能优于经典CC。
Huttenlocher等人[95]提出了一种与其他类型的相似性度量一起使用的方法。他们通过Hausdorff距离(HD)记录通过平移或平移加旋转转换后的二进制图像(边缘检测器的输出)。他们将基于HD的算法与CC进行了比较。尤其是在像素位置受到干扰的图像上，这对于CC来说是问题所在，HD优于CC。
类相关方法的两个主要缺点是相似性度量最大值的平坦性(由于图像的自相似性)和较高的计算复杂性。可以通过预处理或使用边缘或矢量相关性来锐化最大值。 Pratt [145]在配准之前应用了图像过滤功能，以提高对嘈杂或高度相关图像的CC性能。 Van Wie [196]和Anuta [6]采用基于边缘的相关性，该相关性是根据从图像提取的边缘而不是原始图像本身计算的。以这种方式，该方法对参考图像和感测图像之间的强度差异也不那么敏感。这种方法的扩展称为基于矢量的相关性，它使用窗口的各种表示来计算相似性度量。
尽管有上述限制，但类似相关的配准方法仍经常使用，特别是由于其易于实现的硬件，这使其在实时应用中很有用。
4.1.2 傅立叶方法
如果需要加快计算速度，或者如果图像是在变化的条件下获取的，或者图像因频率相关的噪声而损坏，则首选傅里叶方法，而不是类似相关的方法。他们利用频域中图像的傅立叶表示。相位相关方法基于傅立叶位移定理[23]，最初是为翻译图像的配准而提出的。
它计算感测到的图像和参考图像的交叉功率谱，并寻找峰的倒置位置(见图2)。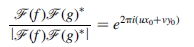
该方法对相关和频率相关的噪声以及不均匀的时变照明干扰显示出强大的鲁棒性。如果要配准的图像很大，则节省的计算时间会更大。
De Castro和Morandi [29]引入了相位相关性的扩展，用于附加的旋转变换。如果图像比例尺也存在变化，则可以使用光谱幅度的极对数映射组合(对应于傅里叶-梅林变换)对图像进行配准和相位相关[31，150]或倒谱滤波器[107]。参考文献[31]描述了扩展算法在遥感(SPOT图像)和医学成像(MR图像)中的应用。在模拟条件下(眼底变形和嘈杂图像的配准)对方法的准确性进行了测试，结果令人满意[34]。
参考文献[210]中通过相位相关和对数极坐标映射记录了仿射失真的图像。参考文献[119]描述了相位相关在3D中的应用。参考文献[6]描述了利用傅立叶变换的另一种应用。作者建议在频域中计算相关性。当应用于边缘表示而不是原始灰度图像时，此方法可以处理多峰图像。 Foroosh等人[61]介绍了通过下采样图像上相位相关性的解析表达式将相位相关性扩展到亚像素配准。
4.1.3 互信息的方法
互信息(MI)方法是此处要审查的基于区域的方法的最后一组。它们最近出现，代表了多模式配准中的领先技术。多峰图像的配准是一项艰巨的任务，但通常需要解决，特别是在医学成像中。比较患者身体的解剖和功能图像可以得出诊断，否则将无法获得诊断。遥感也经常利用更多传感器类型。
源于信息理论的MI是对两个数据集之间统计相关性的一种度量，它特别适合于配准来自不同模态的图像。两个随机变量X和Y之间的MI由下式给出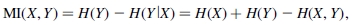
其中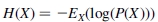
表示随机变量的熵，P(X)是X的概率分布：该方法基于MI的最大化(图3)。通常，通过从粗到精实现提高配准速度解决策略(金字塔式方法)。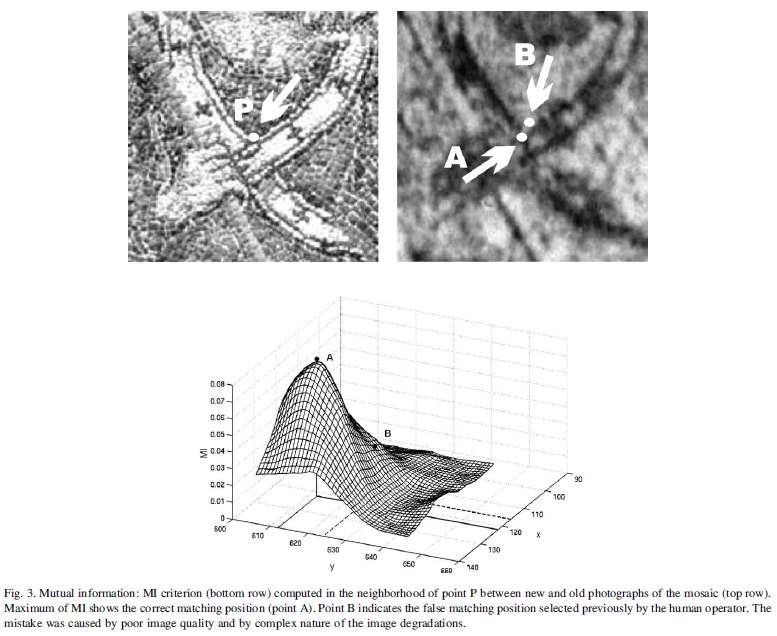
图3.相互信息：在马赛克的新照片和旧照片(顶部行)之间的P点附近计算出的MI准则(底部行)。 MI的最大值显示正确的匹配位置(点A)。 点B指示操作人员先前选择的错误匹配位置。 该错误是由于较差的图像质量和图像降级的复杂性质引起的。
提出这种技术的第一篇文章是Viola和Wells [201]。作者描述了MI在磁共振图像配准以及与真实场景匹配的3D对象模型中的应用。使用梯度下降优化方法将MI最大化。 venaz和Unser [186–188]尝试结合各种方法，解决了MI配准的各个步骤。他们采用Parzen窗进行联合概率计算，并采用Jeeves方法[187]或Marquardt-Levenberg方法[186]来最大化MI。为了加快计算速度，他们使用了样条金字塔[188]。里特(Ritter)等人[152]结合分层搜索策略和模拟退火来找到MI的最大值。 Studholme等人[177]比较了三种类似的信息依赖度量标准：联合熵，MI和规范化的MI(一种新的概念，据称优于其他思想)。他们应用了联合概率分布的离散直方图估计，而不是先前工作中使用的Parzen窗口。通过使用多分辨率爬山算法来实现最大化。他们记录了人脑的MR-CT和MR-PET图像。 Maes等人[120]利用Brent方法和Powell多维方向集方法优化了MI，以记录通过相似变换而不同的人脑的MR，CT和PET图像。参考文献[162]描述了应用于乳房MR图像的心梗。作者建议通过仿射变换和基于样条的自由形式变形的组合来对图像之间存在的整体变形进行建模。 Likar和Pernus [116]研究了在肌肉纤维图像配准中联合概率估计的不同方法的性能。参考文献[143]将基本的MI配准与采用从粗到精加速的版本进行了比较。参考文献[142]中描述了MI与包括归一化CC和梯度相关性在内的其他六种配准方法的比较。参考文献[153]中描述了MI与其他基于区域的相似性(相关系数，相关比)度量之间的关系。使用最大似然估计问题的公式。
上面提到的MI方法适用于整个图像数据，并直接适用于图像强度。 Rangarajan等人[149]在提取的要素(区域边界点)上应用了MI，但是这种方法仍然很少见。类似于信息理论的MI，是基于交叉熵的相似性度量[221]。
4.1.4 优化方法
寻找最小相似度度量(罚函数)或最大相似度度量是一个多维优化问题，其中维数与预期几何变换的自由度相对应。产生全局极限解的唯一方法是在整个图像上进行详尽搜索。尽管这在计算上要求很高，但是如果仅要估计翻译，通常会使用它。
在具有更大自由度的变换的情况下或在更复杂的相似性度量的情况下，需要复杂的优化算法，这些算法分别有助于定位最大值或最小值。参考文献[166]描述了使用高斯-牛顿数值最小化算法来最小化平方差之和，其中使用了投影几何变形。在参考文献[201]中使用梯度下降优化方法找到MI的最大值。参考文献[164]中应用了Levenberg–Marquardt优化方法。以最小化相应像素的强度变化。图像通过投影变换模型和镜头畸变模型进行配准。参考文献[185]描述了Levenberg-Marquardt方法和平方差度量之和的组合。类似地，Wolberg和Zokai [211]使用这种组合来记录透视变形的图像。鲍威尔(Powell)的多维方向设置方法[96]被应用在Maes等人[120]中。 Starink和Backer [174]试图通过模拟退火最小化点对上定义的不相似性度量。
参考文献[97]中介绍了另一种适合多模式数据配准的优化方法。结合MI和相关比证明了其适用性。同样，可以通过金字塔方法加快优化方法的速度。
关于这些优化方法，应该注意一件事。有时，在不相似性度量术语旁边，要最小化的公式也包含所谓的正则化或惩罚项，该正则化或惩罚项将转换与要转换的数据互连起来[82]。这两个术语共同形成了与配准相关的成本函数(能量)，优化方法的目的是使其最小化。在文献中，这种方法可称为能量最小化方法。在刚体变换的情况下，通常会省略正则项，但在非刚性变换(例如，弹性或流体配准方法)中，会出现第5节中更详细的介绍。
4.2 基于特征的方法
我们假设已检测到CP所代表的参考图像和感应图像中的两组特征(点本身，线特征的端点或中心，区域的重心等)。目的是使用它们的空间关系或特征的各种描述符来找到它们之间的成对对应关系。
4.2.1 使用空间关系的方法
如果检测到的特征是模棱两可的或它们的邻域局部变形，通常会使用主要基于特征之间的空间关系的方法。利用关于CP之间的距离及其空间分布的信息。
格什塔比(Ref。[71])描述了基于图匹配算法的配准。他正在评估感测图像中经过特定变换后，落在参考图像中特征旁边给定范围内的特征数量。然后将得分最高的转换参数设置为有效估计。
Stockman等人[175]提出的聚类技术试图匹配由抽象边或线段连接的点。假定的几何模型是相似性变换。对于来自参考图像和感测图像的每对CP，计算将点相互映射的变换参数，并将其表示为变换参数空间中的一个点。紧密映射最多数量特征的变换参数倾向于形成一个簇，而不匹配则随机填充参数空间。检测到聚类，并假设其质心代表匹配参数的最可能矢量。映射功能参数因此与特征对应同时找到。本地错误不会全局影响配准过程。例如，在参考文献[30,72]中实现了聚类技术。
巴罗等人[14]介绍了用于图像配准的倒角匹配。通过最小化图像之间的广义距离来匹配图像中检测到的线特征。 Borgefors [22]提出了一种改进的版本，在此版本中，采用了更好的对应度量，即顺序距离变换和均方根平均值。该算法还采用金字塔式加速。
即使本概述不打算涵盖3D配准方法，在这里也提到了由Besl和McKay [18]引入的著名的迭代最近点(ICP)算法，因为它代表了配准3D形状(包括免费)的关键方法。形式的曲线和曲面)。
4.2.2 使用不变描述符的方法
作为利用空间关系的方法的替代方法，可以使用特征描述来估计特征的对应关系，最好不改变预期图像的变形(见图4)。描述应满足几个条件。最重要的是不变性(来自参考图像和感测图像的相应特征的描述必须相同)，唯一性(两个不同的特征应具有不同的描述)，稳定性(特征的描述在图像中会稍微变形)未知的方式应该接近于原始特征的描述)和独立性(如果特征描述是矢量，则其元素应在功能上独立)。但是，通常并非必须同时(或可以)同时满足所有这些条件，因此有必要找到适当的权衡。
图4.使用不变量描述符的基于特征的方法：在这两个卫星图像中，使用基于复杂矩的不变量来匹配控制点(拐角)[56]。 数字标识相应的CP。 下图显示配准结果。
来自感测图像和参考图像的具有最相似不变描述的特征将配对为相应特征。不变描述类型的选择取决于图像的特征和假定的几何变形。在特征描述符空间中搜索最佳匹配的特征对时，通常会应用带有阈值的最小距离规则。如果需要更鲁棒的算法，则可以更好地处理可疑情况的匹配似然系数[51]是合适的解决方案。 Guest等。建议根据特征匹配的可靠性选择特征[80]。
最简单的特征描述是图像强度函数本身，仅限于特征[1,107]的近邻。为了估计特征对应关系，作者计算了这些邻域的CC。也可以使用其他类型的相似性度量。 Zheng和Chellapa利用了相关系数[219]。
他们假设相似的几何变形。在他们的方法中，首先通过估计光源方向来补偿图像之间的旋转，然后执行基于粗糙到精细相关性的配准。在参考文献[223]中MI用于改善特征对应。
以下参考文献是直观描述的示例，这些描述通常不满足不变描述符的某些提及标准。 Sester等[165]提出通过延伸参数，紧密度，孔数和最小边界矩形的几个特征来描述用作区域特征的森林。为了用星表登记恒星，Murtagh [133]分配给每个点的特征是对周围其他特征的空间分布的描述。参考文献[202]中的武乔维奇和布拉扎科维奇通过最长的结构和参与该相交的所有其他结构之间的角度所形成的特征来表示每个检测到的特征(细长结构的相交)。类似地，Zana [218]通过相关相交线之间的角度描述了每个特征点。蒙特西诺斯(Montesinos)等人[131]提出在检测到的CP附近使用图像函数的差分描述符。 Yang和Cohen [216]使用了物体凸包产生的边界三角形，并在其上计算出仿射几何不变量。
许多作者使用封闭边界区域作为特征。原则上，在区域匹配中可以使用任何不变且可区分的足够的形状描述符。 Peli [141]提出了通过径向矢量进行简单快速的描述，但是这种方法的使用仅限于星形区域。参考文献[65,180]提出了二进制矩阵形式的广义形状描述。
在参考文献[72]中，形状矩阵用于配准旋转和缩放后的卫星图像。在参考文献[112]中提出了轮廓的链码表示作为不变描述，并采用链码相关性度量来寻找对应关系。 Skea等人[171]用球形表示CP的非共线三连体。 Suk [178]提出了用多边形表示的区域的不变形状描述，并在参考文献[179]中进一步发展了这种方法。
大量方法使用基于矩的不变量描述封闭边界区域特征。考虑到最常假定的变形，Hu [93]将矩不变性引入了相似变换。 Flusser和Suk导出了仿射变换不变量[53]，并将其成功用于SPOT和Landsat图像的配准[54]。 Holm [88]提取了封闭边界区域，并提出用其周长，面积，紧实度，矩和矩不变性来表示它们。 Bhattacharya [20]提出了复杂矩的应用。 Brivio等人[24]利用惯性椭圆模拟山中图像的阴影结构。椭圆在这里通过面积，主轴的倾斜度和椭圆率来描述。所有这些属性都是力矩的函数。李等。[112]使用胡的前两个矩作为预选器来匹配闭合轮廓。使用轮廓的链码表示测试候选匹配。文献[35]中描述了一种类似的方法，其中不变矩与链码一起使用。 Sato和Cipolla [163]使用线状特征方向的分布圆矩直接计算了当前几何变形的参数(无需仿射变换)，无需进行对应估计。他们结合了矩和图像的比例空间表示。最近，Flusser和Suk [55]引入了一类新的矩不变量，它们对图像模糊不变，并证明了它们在配准SPOT和AVHRR卫星图像中的性能。本图图等人[16]使用这些不变量来记录相互移位和模糊的数字减影血管造影图像。 Flusser等。参考文献[56]中进一步发展了这种方法。通过引入组合的模糊不变量。参考文献[52]他们推广了以前的不变式来配准3D图像。
特征的基本几何特性的不变组合可以形成面向几何的描述符。 Govindu等人[74]用轮廓点的切线斜率表示从可能旋转的图像中提取的轮廓。他们不是在寻找轮廓对应关系，而是在寻找拟议的描述符分布。通过比较来自参考图像和感测图像的相应分布，可以估计相互的图像旋转。他们也为仿射变换导出了类似类型的描述符。参考文献[73]中详细介绍了该方法的实用方面。 Wang和Chen [205]计算了参考图像和感应图像中线长比的直方图和任意两条线段的角度差直方图。他们假设相似变换。 Griffin和Alexopoulos [77]根据与x轴的夹角和距质心的距离，使用最小封闭圆半径的比率，重心位置的差异以及按字母顺序对邻居进行排序。所有这些方法都跳过了查找特征对应关系的步骤，并直接建立了映射函数参数。
Hsieh等人[91]使用在线特征点上计算出的角度直方图来补偿旋转差。在去除旋转差之后，借助CC找到特征点对应关系。他们将旋转补偿与参考文献[219]中所述的补偿进行了比较。
Shekhar等人[167]组合了不同类型的特征及其描述符。他们将当前的几何变形分解为基本步骤，然后使用特征共识来估计变换参数-每种类型的特征描述符都会对参数的对应值进行投票。然后选择在所有描述符类型上最大化投票数的参数值。
文图拉等人[200]通过各种描述符(椭圆度，角度，细度等)描述图像特征，并通过多值逻辑树(MVLT)表示它们之间的关系。然后，他们比较了参考图像和感测到的图像的MVLT，以找到特征对应关系。 MVLTs和矩不变性一起也应用于参考文献[24]。
当没有先验特征检测未完成并且对于在整个图像上滑动的窗口连续计算不变量时，也可以使用不变描述符。对于平移和旋转的图像，Goshtasby [66]提出从圆形窗口计算矩不变量[93]，然后将CC准则应用于矩窗口表示。 Wong和Hall [213]早些时候使用了类似的想法。除了基于矩的窗口描述外，他们还应用了分层搜索策略来匹配雷达图像和光学图像。
4.2.3 放松方法
作为一致性标记问题(CLP)的解决方案之一，一大套配准方法是基于松弛方法的：将感应图像中的每个特征都标记为参考图像中的特征，因此它是与赋予其他特征对的标签一致[130]。反复考虑要素对的匹配质量并匹配其邻域，重新计算对品质因数，直到达到稳定状态。参考工作由Ranade和Rosenfeld [148]完成。在此，通过某个几何变换变换的特征集的位移定义了特征对的品质因数。此方法可以处理移位的图像，并且可以承受局部图像失真。
王等人[204]通过包括拐角特征的描述扩展了经典的放松。他们使用了拐角清晰度，对比度和倾斜度。该算法可以处理图像中的平移和旋转变形，但是在计算上要求很高。 Medioni和Nevatia [128]使用线特征及其描述符(坐标，方向，平均对比度)。 Cheng和Huang [33]提出了一种基于星号的配准方法，该配准方法考虑了各个特征点以及与邻居的所有链接。 Ton和Jain [190]通过集成MergeSort概念加快了算法的速度。他们的方法适用于移位和旋转的图像。例如，Cheng [32]，Ogawa [136]和Li [113]提出了一种基于松弛的方法，甚至用于相似度变换的图像。文献[147]比较了不同的松弛方法。
CLP问题以及图像配准的另一种解决方案是回溯，其中以递归方式生成一致的标记。参考文献[130]中描述了一种基于回溯的配准方法。
4.2.4 金字塔和小波
通过提及一些尝试通过金字塔方法降低由于大图像尺寸而导致的计算成本的工作，我们结束了有关特征匹配的讨论。
第一次尝试是在1977年进行的。Vanderbrug和Rosenfeld的工作集中在窗口对测试所需的计算量上。在参考文献[197]中，他们首先使用子窗口在参考图像中找到相应窗口的可能候选对象，然后应用全尺寸窗口。他们讨论了子窗口大小的适当选择，以最大程度地减少预期的计算成本。参考文献[160]他们建议首先以较粗的分辨率使用感测到的图像和参考图像，然后在误差测量较小的位置上使用较高分辨率的图像。 Althof等人[4]提出通过仅采取稀疏的规则窗口网格来减少必要的计算负荷，针对这些窗口执行互相关匹配。这些技术是金字塔方法的简单示例。
通常，这种从粗到细的分层策略将应用常规的配准方法，但是它以粗糙分辨率(使用高斯金字塔，简单平均或小波变换系数等生成)从参考图像和感应图像开始。然后，他们逐步提高对应性或映射函数参数的估计，同时提高分辨率。在每个级别，它们都大大减少了搜索空间，从而节省了必要的计算时间。另一个重要的优点在于，首先针对大型特征进行配准，然后对细节进行较小的校正。另一方面，如果在较粗糙的级别识别出错误匹配，则该策略将失败。为了克服这个问题，应在算法中包含回溯或一致性检查。
参考文献[37,208,219]提出了将CC与采用求和金字塔的金字塔方法相结合(较粗糙级别的像素值对应于先前级别的像素值的总和)，中位数金字塔和平均金字塔。分别。 Wong和Hall [214]将SSDA方法与金字塔形加速相结合。 Wang和Chen [205]提取了每个分辨率级别的特征(封闭边界区域的质心)，并从角度差和线长比的直方图中找到了几何变形的参数，如上所述。 Thevenaz等人分别应用了基于三次样条的金字塔，并分别最小化了图像之间的均方强度差[184]和MI最大化[187]。 Sharma和Pavel [166]使用多分辨率拉普拉斯金字塔进行红外和雷达图像配准。 Kumar等人[102]结合了不同类型的金字塔(拉普拉斯，高斯)和不同的相似性度量(CC，平方差之和)来配准航空视频序列。参考文献[169]中使用了金字塔形式的非线性最小-最大滤波器。
最近，由于金字塔方法固有的多分辨率特征，建议对图像进行小波分解。方法的不同之处在于所应用的小波类型和用于查找对应关系的小波系数集。最常用的方法是通过依次使用两个滤波器(低通滤波器L和高通滤波器H)依次对图像进行滤波，将图像递归分解为四组系数(LL，HL，LH，HH)。列。
Turcajova和Kautsky [193]在规则的点网格上测试了各种正交和双正交小波(它们使用LL系数)以及CC，以配准仿射变换图像。样条双正交小波和Haar小波的性能优于其他小波。 Fonseca和Costa [58]检测到LH和HL系数的模数最大值，并寻找相关系数的最大值，该相关系数是根据在检测到的最大值的小范围内的LL系数计算得出的。 Djamdji等人[41]仅使用HH系数。 Le Moigne [105]应用Daubechies小波来配准Landsat图像和AVHRR数据。他们提取了LH和HL频率系数，并通过CC找到了对应关系。 Liu et al [118]提出了Gabor小波变换和配准残差的高斯模型的应用。 You和Bhattacharya [217]使用小波系数的最大紧凑模糊集作为特征，使用HD作为相似性度量。参考文献[176]研究了通过Daubechies和Haar小波进行配准的鲁棒性。
4.2.5 摘要
当图像没有很多突出细节并且独特信息是由灰度/颜色而不是局部形状和结构提供时，最好使用基于区域的方法。基于区域的方法有两个主要限制。参考图像和感应图像必须具有某种“相似”的强度函数，或者是相同的(然后可以使用类似相关的方法)，或者至少是统计相关的(通常在多模式配准中发生)。
从几何角度来看，使用基于区域的方法时，仅允许图像之间的平移和很小的旋转(尽管基于区域的方法可以推广到完全旋转和缩放，但由于计算量大，实际上没有任何意义)。为了加快搜索速度，基于区域的方法通常采用金字塔图像表示法和复杂的优化算法来查找相似度矩阵的最大值。
当局部结构信息比图像强度携带的信息重要时，通常会应用基于特征的匹配方法。它们可以记录性质完全不同的图像(例如航空照片和地图)，并且可以处理复杂的图像间失真。基于特征的方法的共同缺点是各个特征可能难以检测和/或在时间上不稳定。所有基于特征的匹配方法的关键点是具有判别性和鲁棒性的特征描述符，这些特征描述符对于图像之间的所有假定差异都是不变的。
5.变换模型估计
在建立了特征对应关系之后，便构建了映射功能。它应该转换感测到的图像以使其覆盖在参考图像上。在映射函数设计中采用了来自感测图像和参考图像的CP的对应关系以及在感测到的图像变换之后相应的CP对应该尽可能接近的事实。
要解决的任务包括选择映射函数的类型(参见图5)及其参数估计。映射函数的类型应对应于所感测图像的假定几何变形，图像获取方法(例如，与扫描仪有关的变形和误差)以及所需的配准精度(刚体点的误差分析)参考文献[48]中引入了基于配准的方法。
图5.各种映射函数的示例：相似变换(左上)，仿射变换(右上)，透视投影(左下)和弹性变换(右下)。
在特殊情况下，几何变形是部分已知的，例如当存在由采集设备和/或场景几何形状引起的变形的模型时，可以执行基于变形逆的预校正(例如，在参考文献[94,168,181]中，作者对地球的形状和旋转，卫星轨道和传感器的扫描几何形状)。
映射函数的模型可以根据它们用作支持的图像数据量分为两大类。全局模型使用所有CP来估计一组对整个图像有效的映射函数参数。另一方面，局部映射功能将图像视为补丁的组合，并且功能参数取决于其在图像中的支持位置。它导致图像的细分，通常是三角剖分，并导致分别为每个面片定义映射函数的参数。
从另一个角度来看，可以根据用于参数计算的CP的覆盖精度对映射功能进行分类。内插函数将感测到的图像CP精确地映射到参考图像CP上，而近似函数则试图在最终映射的精度和对映射函数的特性施加的其他要求之间找到最佳折衷。由于通常假定CP坐标不精确，因此近似模型更为常见。
5.1 全局映射模型
最常用的全局模型之一使用低度的二元多项式。相似度转换是最简单的模型-仅包含旋转，平移和缩放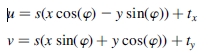
该模型通常称为“形状保留映射”，因为它保留了角度和曲率，并且由两个CP明确确定。
仿射变换稍微通用一些，但仍然是线性模型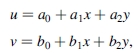
可以将平行四边形映射到正方形。该模型由三个非共线CP定义，保留了直线和直线平行度。假设照相机到场景的距离比扫描区域的大小大，照相机是完美的(针孔照相机)，场景平坦并且当前的几何变形，则可以用于多视图配准没有本地因素。
如果不满足相机到场景距离的条件，则透视投影模型
应该使用。该模型准确地描述了由针孔相机拍摄的平坦场景的变形，其光轴不垂直于场景。它可以将一个普通的四边形映射到一个正方形，同时保留直线，并且由四个独立的CP确定。
稍微违反这些假设可能会导致使用二阶或三阶多项式模型。在实际应用中通常不使用高阶多项式，因为在与参考图像对齐时，它们可能会不必要地在远离CP的区域扭曲检测到的图像。
通常，CP的数量通常高于确定映射函数所需的最小数量。然后通过最小二乘拟合来计算映射函数的参数，以便多项式最小化CP的平方误差之和。这样的映射功能不能将CP精确地映射到其对应对象上。事实证明，这种方法对于卫星图像非常有效且准确。
5.2 本地映射模型
但是，全局多项式映射不能正确处理局部变形的图像。例如，在医学成像和机载成像中会发生这种情况。最小二乘技术在整个图像上平均均衡局部几何变形，这是不希望的。图像的局部区域应在配准时考虑到有关局部几何变形的可用信息。
在这种情况下，几位作者已经证明了本地或至少本地敏感的配准方法优于全局配准方法(Goshtasby [69]，Ehlers和Fogel [46]，Wiemker [209]和Flusser [50]等)。 。加权最小二乘法和加权均值方法[69]通过对原始最小二乘方法引入微小的变化，获得了局部配准图像的能力。称为分段线性映射[67]和分段三次映射[68]的局部方法与Akima的五次方法[209]结合使用基于CP的图像三角剖分和局部映射函数集合的组合，每个函数均在一个有效范围内有效三角形。这些方法属于插值方法的组。
5.3 通过径向基函数进行映射
径向基函数是一组全局映射方法的代表，但它们甚至能够处理局部变化的几何变形。生成的映射函数具有平移的径向对称函数和低阶多项式的线性组合的形式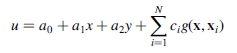
对于v。
最初，它们是为插补不规则曲面而开发的。它们的名称“径向”反映了每个点上函数值的重要属性-它仅取决于点到CP的距离，而不是其特定位置。多二次方，倒数二次方，高斯函数，Wendland函数和薄板样条线是图像配准中使用的径向基函数的几个示例。
参考文献[46]描述了多二次方在机载遥感中的应用以及与三阶多项式方法的比较。参考文献[209]给出了与Akima方法的比较。参考文献[117]中显示了多二次方的医学应用。参考文献[60]中列出了Wendland在医学图像配准中应用的功能。这些功能对全局的影响很小，甚至可以通过这种方法很好地记录局部变形。该属性对于配准主要在局部发生变化的医学图像很有用。
径向基函数最常用的代表是薄板样条(TPS)，其中径向项的形式为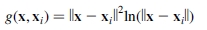
(有关各自的数学背景，请参见Duchon [44]和Wahba [203])。尽管它们已经在机械和工程领域中使用了数十年[84]，但由Grimson [78]和Bookstein [21]引入了图像分析社区。 TPS可以看作是一块非常薄的板，它固定在参考图像中CP所确定的位置上，高度由感测图像中相应CP的x或y坐标给出[70]。 TPS最小化了势能的二次方变化函数，该函数反映了函数变化量，并且对于良好的映射函数来说应该很小。可以选择配准的类型：精确插值[70]，近似[159]或考虑到各向异性界标误差[157]的广义近似。参考文献[156]中找到了针对基于TPS的医学图像配准的全面研究。
TPS配准可提供良好的结果，但是计算可能非常耗时，即CP数量很多。在保持合理准确度的同时，已经对降低TPS评估复杂性的方法给予了极大的关注。 Flusser [50]通过更简单的函数提出了在正方形或三角形区域上TPS的自适应近似。 Beatson和Newsam [15]将Greengard [75]的较早方法改编为径向功能的多极扩展。 Powell [144]通过TPS制表降低了计算成本。 Barrodale等人[13]关注TPS系数的快速和稳健计算。
许多论文都在比较薄板样条和其他贴图功能的性能。在参考文献[57,70,209]中，当配准航空图像时，将它们与多项式和多元函数进行比较。参考文献[8]将TPS与高斯径向基函数以及考虑其局部特性的多二次方进行了比较。结论是，TPS用作图像配准的映射函数时具有良好的属性，而其他径向基函数更适合其他应用，例如图像扭曲和变形[8]。
TPS并不是用于映射功能设计的样条线族的唯一代表。平移三次B样条的线性组合用于回波平面图像的配准[103]。在[39]中提出了另一种基于样条的函数，弹性体样条(EBS)。它是从均质各向同性弹性材料承受载荷的平衡位移的描述演变而来的。要记录的图像数据中描绘的身体组织通常具有弹性材料的特性。 EBS用于记录乳房的3D MRI图像。作者声称EBS在他们的实验中胜过了TPS。
5.4 弹性套准
配准具有相当复杂和/或局部失真的图像的另一种方法是不使用任何参数映射函数，因为几何变形的估计被简化为对“最佳”参数的搜索。这个想法是由Bajcsy等人[10]提出的，通常被称为弹性配准。
图像被视为一块橡胶片，在其上施加拉伸图像的外力和由刚度或平滑度约束定义的内力，以使其在最小程度的弯曲和拉伸下对齐。配准的特征匹配和映射功能设计步骤是同时完成的。这是弹性方法的优点之一，因为未知复杂变形所固有的特征描述符，并且难以以传统方式建立特征对应关系。通过以迭代方式定位最小能量状态来实现配准。通常采用金字塔方法。外力可以从相似度函数的局部优化中得出，该相似度函数由强度值或边界结构的对应关系[38]定义。在参考文献[140]中，没有使用外力，并且将根据边界结构的对应关系得出的规定位移纳入了弹性图像变形中。
弹性定位的缺点是图像变形非常局限。这可以通过流体配准来处理。流体配准方法利用粘性流体模型来控制图像变换。在高斯传感器模型的导数的控制下，参考图像在此建模为浓稠的流体，该流体流出以匹配感测到的图像。
这种方法主要用于医疗应用[25]。
这种方法的弱点是在配准过程中引入的模糊性。 Lester和Arridge [110]提出仅使用流体模型来寻找CP的对应关系，然后通过薄板样条来处理正变换。文献[212]中找到了三种基于液剂的配准方法的比较。
非刚性方法的另一个示例是基于扩散的配准，水平集配准和基于光流的配准。扩散配准将对象轮廓和其他特征作为膜处理，从而设置几何约束。参考文献[189]中描述了这种方法的三种变体。 Andersen和Nielsen提出了不同的解决方案[5]。 Vemuri等人[199]引入了基于水平集演化并沿着各自法线移动的弹性配准方法。最后，最初通过估计图像之间的相对运动来激发光流方法[19]。光流配准的类别涵盖了大量方法，超出了本调查的范围。
6.图像重采样和变换
在上一步中构建的映射函数用于变换感测的图像，从而配准图像。可以以向前或向后的方式实现变换。可以使用估计的映射函数直接转换感测图像中的每个像素。这种方法称为正向方法，实施起来很复杂，因为它会在输出图像中产生孔和/或重叠(由于离散化和舍入)。因此，通常选择后向方法。使用目标像素的坐标(与参考图像相同的坐标系)和估计的映射函数的反函数确定来自感测图像的配准图像数据。图像插值发生在规则网格上的感应图像中。这样，在输出图像中既不会出现孔也不会出现重叠。
插值本身通常是通过将图像与插值内核进行卷积来实现的。最佳插值法-二维Sinc函数-由于其无限的范围而在实践中难以实现。因此，在文献中已经研究了许多更简单的有限支持插值。为了减少计算成本，优选地考虑了可分离的插值。可分离性使m * m 2D卷积替换为(m + 1)1D卷积，速度更快。
最近邻函数，双线性和双三次函数(参见图6)，二次样条[42,191]，三次B样条[89]，高阶B样条[108]，Catmull-Rom主样条[100,184]，高斯[ 7]和截断的Sinc函数[182]属于最常用的插值。 Meijering等人[129]研究了高阶多项式核(五阶和化脓性)。但是，他们的实验表明，与三次插值相比，边际改进只是很大的计算成本。
图6.图像插值方法：原始图像(左上)使用三种不同的插值技术放大了五倍：最近邻(右上)，双线性(左下)和双三次(右下)。
过去几年中已发表了几篇有关重采样技术的调查论文。参考文献[138]进行了详细的调查和方法比较。用于2D图像和参考文献[76] 3D数据。 Thevenaz等人[182]关注消除不需要的插值伪像。 Lehman等人[109]发表了一篇调查文章，内容涵盖了主要的内插方法(sinc函数的各种版本，最近邻，线性，二次，三次，三次B样条，拉格朗日和高斯核)，重点是医学成像应用。他们使用空间和傅立叶分析对其进行了比较，并测试了计算复杂度以及内插误差。最近，Thevenaz等人[183]提出了另一种图像重采样方法。与其他方法不同，它们的重采样功能不必插值图像灰度级。他们宁愿插值作为灰度的某些函数计算的值。作者已经证明了这种方法优于传统的插值技术。
即使就转换后的图像的准确性和视觉外观而言，双线性插值的性能优于高阶方法，但它可能在精度和计算复杂度之间提供了最佳折衷，因此它是最常用的方法。当几何变换涉及所感测图像的显着放大时，建议使用三次插值。在大多数情况下，由于重采样图像中存在伪影，应避免最近的邻居插值。唯一的例外是当要变换的图像强度较低时，并且我们不想通过高阶插值法引入“合成”灰度/颜色。
7.图像配准精度的评估
不管特定的图像，使用的配准方法和应用领域如何，都非常需要为用户提供估计实际配准的准确性的估计。准确性评估是一个不平凡的问题，部分是因为错误可能会在每个阶段拖入配准过程，部分是因为很难区分配准错误和图像内容中的实际物理差异。在本节中，我们回顾了基本的错误类别和用于测量套准准确性的方法。
本地化错误。由于CP坐标检测不准确而导致的位移称为定位误差。作为检测方法的固有误差，不能直接在给定图像上测量定位误差。但是，从计算机仿真研究和地面真相比较中，大多数CP检测方法的平均精度对于各种图像类型都是已知的。在特定情况下，这可用于估计预期的定位误差。可以通过为给定数据选择“最佳”特征检测算法来减少定位误差，但是通常在检测到的CP候选数量和平均定位误差之间要权衡取舍。有时，我们宁愿拥有更多具有较高定位误差的CP，而不是只有少数几个，但可以更精确地检测到。
匹配错误。建立CP候选之间的对应关系时，通过错误匹配的数量来衡量匹配误差。这是一个严重的错误，通常会导致配准过程失败，应避免使用。幸运的是，在大多数情况下，可以通过强大的匹配算法来确保这一点。可以通过一致性检查来识别错误匹配，将两种不同的匹配方法应用于同一组CP候选者。
仅将通过这两种方法找到的那些对视为有效CP对，其他候选点则从进一步处理中排除。如果没有其他可靠的匹配方法，则可以通过交叉验证来识别错误的CP对。在每个步骤中，我们从一组CP中排除一对，然后计算映射参数(例如平移矢量和旋转角度)。然后，我们检查此模型将排除点相互映射的程度。如果它们的位移低于给定的阈值，则它们被视为有效的CP对。
对齐错误。通过术语对准误差，我们表示用于配准的映射模型与实际图像间几何失真之间的差异。由于两个不同的原因，在实践中始终存在对准误差。所选映射模型的类型可能不对应于实际失真和/或未精确计算模型的参数。前一种情况是由于缺乏有关几何变形的先验信息而引起的，而后者则是由于CP数量不足和/或其定位误差引起的。
对准误差可以通过几种方法进行评估。最简单的度量是CP的均方误差(CPE)。尽管通常使用，但它不是良好的对准误差度量。实际上，它仅量化所选映射模型对CP坐标的拟合程度。对于任何CP集，只需选择具有足够自由度的映射模型即可达到零CPE(这种众所周知的现象在数值分析中称为“过拟合”)。
另一方面，较大的CPE可能由CP定位错误引起，并不一定反映较差的配准精度。
与CPE非常相似的是所谓的测试点误差(TPE)。测试点是故意从映射参数的计算中排除的CP。无法通过过度拟合将TPE设置为零，这使其比CPE更有意义。但是，测试点的定位误差可能会对这种措施产生负面影响。仅当有足够数量的CP可用时，才可以使用此方法。否则，排除多个CP可能会导致映射参数的估算不准确。在医疗应用中，CP可能远离您感兴趣的区域。因此，Fitzpatrick等[47,49]提出了检测感兴趣区域内的解剖学点并将其用作测试点(称为“目标点”)的方法。可以扩展TPE的概念，以便测量相应的“测试”线或表面之间的距离[134,139]。
估计对准精度的另一种方法是使用多个提示进行一致性检查。在此，将通过研究方法配准的图像与通过另一比较方法配准的同一图像进行比较(通过图像空间中的适当度量)。作为比较方法，我们最好使用“黄金标准方法”，该方法通常被认为是在特定应用领域或给定图像类型中最佳的方法(黄金标准方法起着类似于地面真实性的作用)。这种方法通常用于医学成像[47,207]。在遥感，计算机视觉和工业检查等不存在任何黄金标准的应用领域中，我们将具有不同性质的任何方法作为比较方法。配准结果之间的细微差异表明(尽管不能保证)良好的配准准确性。
当一组至少两个感测到的图像被配准到同一参考[34,63,87,215]时，可以采用不同的一致性检查。所感测到的图像也可以使用同一套CP进行套准，从而提供另一套映射参数。使用映射的传递性，我们为每个感测图像获得两组映射参数，即两个配准图像，其理论上应该相同。测试点的位移可以用作质量度量。
最后，应该提到最古老的配准准确性评估方法-领域专家的视觉评估。它仍然至少被用作上述客观误差度量的补充。
估计配准算法的准确性是配准过程的重要组成部分。如果不进行定量评估，则无法接受任何配准方法来进行实际使用。在验证刚体配准方面已经做了大量工作(最全面的案例研究可能是范德比尔特大学项目[207])，而非线性，局部和弹性配准方法的验证仍处于起步阶段。
8.当前趋势和未来展望
在集成和分析来自各种来源的信息时，图像配准是最重要的任务之一。这是图像融合，变化检测，超分辨率成像以及建筑图像信息系统等关键阶段。本文对经典和最新的配准方法进行了概述，并根据其性质以及四个主要配准步骤对其进行了分类。尽管已经完成了大量工作，但是自动图像配准仍然是一个悬而未决的问题。具有复杂的非线性和局部失真的图像配准，多模式配准以及N-D图像配准(其中N> 2)属于当前最具挑战性的任务。
在配准具有非线性，局部依赖的几何失真的图像时，我们面临两个基本问题：如何匹配CP和用于配准的映射功能。尽管第二个问题可以通过使用适当的径向基函数至少在理论上解决，但是第一个问题由于其性质而通常无法解决。由于图像之间的变形可以是任意的，因此我们不能使用任何自动匹配方法。这里的另一个概念性问题是如何区分图像变形和场景的真实变化。
在多模式配准中，MI技术已成为标准参考，主要是在医学成像中。然而，作为基于区域的技术，MI具有主要局限性。为了克服它们，一些作者将MI与其他(最好是基于特征的)方法相结合，以获得更高的鲁棒性和可靠性。为了加快计算速度，他们经常采用金字塔图像表示以及快速优化算法。不幸的是，当图像具有明显的旋转和/或缩放比例差异时，这些方法要么失败要么变得非常耗时。该领域的未来发展可能会更多地关注基于特征的方法，其中适当的不变性和模态不敏感特征可以为配准提供良好的平台。此外，我们相信利用特定传感器特性的新的特定于应用程序的方法会很快出现在遥感中。
N-D图像配准的主要困难在于其计算复杂性。尽管计算机的速度一直在增长，但是仍然需要减少方法的计算时间。方法的复杂性以及数据的大小仍在增长(更高的分辨率，更高的维数，更大的扫描区域大小)。而且，对更高鲁棒性和配准精度的需求通常使用迭代或回溯来实施解决方案，这也增加了该方法的计算复杂度。
将来，最终配准方法的想法能够识别给定任务的类型并自行决定最合适的解决方案，这可以激励专家系统的开发。它们将基于各种方法的组合，以寻求特定结果的共识。
致谢
这项工作得到了捷克共和国赠款局第102/01 / P065号赠款的支持。
参考文献
[1] S. Abdelsayed, D. Ionescu, D. Goodenough, Matching and registration method for remote sensing images, Proceedings of the International Geoscience and Remote Sensing Symposium IGARSS’95, Florence, Italy, 1995, pp. 1029–1031.
[2] H.S. Alhichri, M. Kamel, Virtual circles: a new set of features for fast image registration, Pattern Recognition Letters 24 (2003) 1181–1190.
[3] W.S.I. Ali, F.S. Cohen, Registering coronal histological 2-D sections of a rat brain with coronal sections of a 3-D brain atlas using geometric curve invariants and B-spline representation, IEEE Transactions on Medical Imaging 17 (1998) 957–966.
[4] R.J. Althof, M.G.J. Wind, J.T. Dobbins, A rapid and automatic image registration algorithm with subpixel accuracy, IEEE Transactions on Medical Imaging 16 (1997) 308–316.
[5] P.R. Andersen, M. Nielsen, Non-rigid registration by geometryconstrained diffusion, Medical Image Analysis 5 (2001) 81–88.
[6] P.E. Anuta, Spatial registration of multispectral and multitemporal digital imagery using Fast Fourier Transform, IEEE Transactions on Geoscience Electronics 8 (1970) 353–368.
[7] C.R. Appledorn, A new approach to the interpolation of sampled data, IEEE Transactions on Medical Imaging 15 (1996) 369–376.
[8] N. Arad, N. Dyn, D. Reisfeld, Y. Yeshurun, Image warping by radial basis functions: application to facial expressions, CVGIP: Graphical Models and Image Processing 56 (1994) 161–172.
[9] M.A. Audette, F.P. Ferrie, T.M. Peters, An algorithmic overview of surface registration techniques for medical imaging, Medical image Analysis 4 (2000) 201–217.
[10] R. Bajcsy, S. Kovacic, Multiresolution elastic matching, Computer Vision, Graphics and Image Processing 46 (1989) 1–21.
[11] S. Banerjee, D.P. Mukherjee, D.D. Majumdar, Point landmarks for registration of CT and NMR images, Pattern Recognition Letters 16 (1995) 1033–1042.
[12] D.I. Barnea, H.F. Silverman, A class of algorithms for fast digital image registration, IEEE Transactions on Computing 21 (1972) 179–186.
[13] I. Barrodale, D. Skea, M. Berkley, R. Kuwahara, R. Poeckert, Warping digital images using thin plate splines, Pattern Recognition 26 (1993) 375–376.
[14] H.G. Barrow, J.M. Tenenbaum, R.C. Bolles, H.C. Wolf., Parametric correspondence and chamfer matching: Two new techniques for image matching. Proceedings of the Fifth International Joint Conference on Artificial Intelligence, Cambridge, Massachusetts, 1977, pp. 659–663.
[15] R.K. Beatson, G.N. Newsam, Fast evaluation of radial basis functions, Computers Mathematical Applications 24 (1992) 7–19.
[16] Y. Bentoutou, N. Taleb, M. Chikr El Mezouar, M. Taleb, J. Jetto, An invariant approach for image registration in digital subtraction angiography, Pattern Recognition 35 (2002) 2853–2865.
[17] R. Berthilsson, Affine correlation. Proceedings of the International Conference on Pattern Recognition ICPR’98, Brisbane, Australia, 1998, p. 1458–1461.
[18] P.J. Besl, N.D. McKay, A method for registration of 3D shapes, IEEE Transactions on Pattern Analysis and Machine Intellinegce 14 (1992) 239–254.
[19] S.S. Beuchemin, J.L. Barron, The computation of optical flow, ACM Computing Surveys 27 (1995) 433–467.
[20] D. Bhattacharya, S. Sinha, Invariance of stereo images via theory of complex moments, Pattern Recognition 30 (1997) 1373–1386.
[21] F.L. Bookstein, Principal warps: Thin-plate splines and the decomposition of deformations, IEEE Transactions on Pattern Analysis and Machine Intelligence 11 (1989) 567–585.
[22] G. Borgefors, Hierarchical chamfer matching: a parametric edge matching algorithm, IEEE Transactions on Pattern Analysis and Machine Intelligence 10 (1988) 849–865.
[23] R.N. Bracewell, The Fourier Transform and Its Applications, McGraw-Hill, New York, 1965.
[24] P.A. Brivio, A.D. Ventura, A. Rampini, R. Schettini, Automatic selection of control points from shadow structures, International Journal of Remote Sensing 13 (1992) 1853–1860.
[25] M. Bro-Nielsen, C. Gramkow, Fast fluid registration of medical images, In Proceedings Visualization in Biomedical Computing (VBC’96), 1131, Springer Lecture Notes in Computer Science, Hamburg, Germany, 1996, pp. 267–276.
[26] L.G. Brown, A survey of image registration techniques, ACM Computing Surveys 24 (1992) 326–376.
[27] S.C. Cain, M.M. Hayat, E.E. Armstrong, Projection-based image registration in the presence of fixed-pattern noise, IEEE Transactions on Image Processing 10 (2001) 1860–1872.
[28] J. Canny, A computational approach to edge detection, IEEE Transactions on Pattern Analysis and Machine Intelligence 8 (1986) 679–698.
[29] E.D. Castro, C. Morandi, Registration of translated and rotated images using finite Fourier transform, IEEE Transactions on Pattern Analysis and Machine Intelligence 9 (1987) 700–703.
[30] S.H. Chang, F.H. Cheng, W.H. Hsu, G.Z. Wu, Fast algorithm for point pattern matching: Invariant to translations, rotations and scale changes, Pattern Recognition 30 (1997) 311–320.
[31] Q. Chen, M. Defrise, F. Deconinck, Symmetric phase-only matched filtering of Fourier–Mellin transform for image registration and recognition, IEEE Transactions on Pattern Analysis and Machine Intellingence 16 (1994) 1156–1168.
[32] F.H. Cheng, Point pattern matching algorithm invariant to geometrical transformation and distortion, Pattern Recognition Letters 17 (1996) 1429–1435.
[33] J.K. Cheng, T.S. Huang, Image registration by matching relational structures, Pattern Recognition 17 (1984) 149–159.
[34] A.V. Cideciyan, Registration of ocular fundus images, IEEE Engineering in Medicine and Biology 14 (1995) 52–58.
[35] X. Dai, S. Khorram, A feature-based image registration algorithm using improved chain-code representation combined with invariant moments, IEEE Transactions on Geoscience and Remote Sensing 37 (1999) 2351–2362.
[36] X. Dai, S. Khorram, Development of a feature-based approach to automated image registration for multitemporal and multisensor remotely sensed imagery, International Geoscience and Remote Sensing Symposium IGARSS’97, Singapore, 1997, pp.
243–245.
[37] P. Dani, S. Chaudhuri, Automated assembling of images: Image montage preparation, Pattern Recognition 28 (1995) 431–445.
[38] C. Davatzikos, J.L. Prince, R.N. Bryan, Image registration based on boundary mapping, IEEE Transactions on Medical Imaging 15 (1996) 112–115.
[39] M.H. Davis, A. Khotanzad, D.P. Flaming, S.E. Harms, A physicsbased coordinate transformation for 3D image matching, IEEE Transactions on Medical Imaging 16 (1997) 317–328.
[40] L. Ding, A. Goshtasby, M. Satter, Volume image registration by template matching, Image and Vision Computing 19 (2001) 821–832.
[41] J.P. Djamdji, A. Bajaoui, R. Maniere, Geometrical registration of images: the multiresolution approach, Photogrammetric Engineering and Remote Sensing 53 (1993) 645–653.
[42] N.A. Dodgson, Quadratic interpolation for image resampling, IEEE Transactions on Image Processing 6 (1997) 1322–1326.
[43] L. Dreschler, H. Nagel, Volumetric model and 3-D trajectory of a moving car derived from monocular TV-frame sequence of a street scene, Proceedings of the Interantional Joint Conference on Artificial Intelligence, Vancouver, Canada, 1981, pp. 692–697.
[44] J. Duchon, Interpolation des fonctions de deux variables suivant le principle de la flexion des plaques minces, RAIRO Analytical Nume´ricals 10 (1976) 5–12.
[45] M. Ehlers, Region-based matching for image registration in remote sensing databases, Proceedings of the International Geoscience and Remote Sensing Symposium IGARSS’91, Espoo, Finland, 1991, pp.
2231–2234.
[46] M. Ehlers, D.N. Fogel, High-precision geometric correction of airborne remote sensing revisited: the multiquadric interpolation, Proceedings of SPIE: Image and Signal Processing for Remote Sensing 2315 (1994) 814–824.
[47] J.M. Fitzpatrik, Detection failure, assessing success, in: J.V. Hajnal, D.L.G. Hill, D.J. Hawkes (Eds.), Medical Image Registration, CRC Press, Baton Rouge, Florida, 2001, pp. 117–139.
[48] J.M. Fitzpatrik, J.B. West, The distribution of target registration error in rigid-body point-based registration, IEEE Transactions on Medical Imaging 20 (2001) 917–927.
[49] J.M. Fitzpatrik, J.B. West, C.R. Maurer Jr., Predicting error in rigidbody point-based registration, IEEE Trasnactions on Medical Imaging 17 (1998) 694–702.
[50] J. Flusser, An adaptive method for image registration, Pattern Recognition 25 (1992) 45–54.
[51] J. Flusser, Object matching by means of matching likelihood coefficients, Pattern Recognition Letters 16 (1995) 893–900.
[52] J. Flusser, J. Boldys, B. Zitova´, Moment forms invariant to rotation and blur in arbitrary number of dimensions, IEEE Transactions on Pattern Analysis and Machine Intelligence 25 (2003) 234–246.
[53] J. Flusser, T. Suk, Pattern recognition by affine moment invariants, Pattern Recognition 26 (1993) 167–174.
[54] J. Flusser, T. Suk, A moment-based approach to registration of images with affine geometric distortion, IEEE Transactions on Geoscience and Remote Sensing 32 (1994) 382–387.
[55] J. Flusser, T. Suk, Degraded image analysis: an invariant approach, IEEE Transactions on Pattern Analysis and Machine Intelligence 20 (1998) 590–603.
[56] J. Flusser, B. Zitova´, Combined invariants to linear filtering and rotation, International Journal of Pattern Recognition and Artificial Intelligence 13 (1999) 1123–1136.
[57] D.N. Fogel, Image rectification with radial basis functions: Application to RS/GIS data integration, Proceedings of the Thirrd International Conference on Integrating GIS and Environmental Modelling, CD-ROM, Santa Fe, New Mexico, 1996, 19 pp.
[58] L.M.G. Fonseca, M.H.M. Costa, Automatic registration of satellite images, Proceedings of the Brazilian Symposium on Computer Graphic and Image Processing, Brazil, 1997, pp. 219–226.
[59] L.M.G. Fonseca, B.S. Manjunath, Registration techniques for multisensor remotely sensed imagery, Photogrammetric Engineering and Remote Sensing 62 (1996) 1049–1056.
[60] M. Fornefett, K. Rohr, H.S. Stiehl, Radial basis functions with compact support for elastic registration of medical images, Image and Vision Computing 19 (2001) 87–96.
[61] H. Foroosh, J.B. Zerubia, M. Berthod, Extension of phase correlation to subpixel registration, IEEE Transactions on Image Processing 11 (2002) 188–200.
[62] W. Fo¨rstner, E. Gu¨lch, A fast operator for detection and precise location of distinct points, corners and centers of circular features, Proceedings of the ISPRS Workshop on Fast Processing of Photogrammetric Data, Interlaken, Switzerland, 1986, pp. 281–305.
[63] P.A. Freeborough, R.P. Woods, N.C. Fox, Accurate registration of serial 3D MR brain images and its application to visualizing change in neurodegenerative disorders, Journal of Computer Assisted Tomography 20 (1996) 1012–1022.
[64] B.K. Ghaffary, A.A. Sawchuk, A survey of new techniques for image registration and mapping, Proceedings of the SPIE: Applications of Digital Image Processing 432 (1983) 222–239.
[65] A. Goshtasby, Description and discrimination of planar shapes using shape matrices, IEEE Transactions on Pattern Analysis and Machine Intelligence 7 (1985) 738–743.
[66] A. Goshtasby, Template matching in rotated images, IEEE Transactions on Pattern Analysis and Machine Intelligence 7 (1985) 338–344.
[67] A. Goshtasby, Piecewise linear mapping functions for image registration, Pattern Recognition 19 (1986) 459–466.
[68] A. Goshtasby, Piecewise cubic mapping functions for image registration, Pattern Recognition 20 (1987) 525–533.
[69] A. Goshtasby, Image registration by local approximation methods, Image and Vision Computing 6 (1988) 255–261.
[70] A. Goshtasby, Registration of images with geometric distortions, IEEE Transactions on Geoscience and Remote Sensing 26 (1988) 60–64.
[71] A. Goshtasby, G.C. Stockman, Point pattern matching using convex hull edges, IEEE Transactions on Systems, Man and Cybernetics 15 (1985) 631–637.
[72] A. Goshtasby, G.C. Stockman, C.V. Page, A region-based approach to digital image registration with subpixel accuracy, IEEE Transactions on Geoscience and Remote Sensing 24 (1986) 390–399.
[73] V. Govindu, C. Shekhar, Alignment using distributions of local geometric properties, IEEE Transactions on Pattern Analysis and Machine Intelligence 21 (1999) 1031–1043.
[74] V. Govindu, C. Shekhar, R. Chellapa, Using geometric properties for correspondence-less image alignment, Proceedings of the International Conference on Pattern Recognition ICPR’98, Brisbane, Australia, 1998, pp. 37–41.
[75] L. Greengard, V. Rokhlin, A fast algorithm for particle simulations, Journal of Computers and Physics 73 (1987) 325–348.
[76] G.J. Grevera, J.K. Udupa, An objective comparison of 3D image interpolation methods, IEEE Transactions an Medical Imaging 17 (1998) 642–652.
[77] P.M. Griffin, C. Alexopoulos, Point pattern matching using centroid bounding, IEEE Transactions on Systems, Man and Cybernetics 19 (1989) 1274–1276.
[78] W.E.L. Grimson, A computational theory of visual surface interpolation, Philosphical Transactions of the Royal Society of London, B 298 (1982) 395–427.
[79] S. Growe, R. Tonjes, A knowledge based approach to automatic image registration, Proceedings of the IEEE International Conference on Image Processing ICIP’97, Santa Barbara, California, 1997, pp. 228–231.
[80] E. Guest, E. Berry, R.A. Baldock, M. Fidrich, M.A. Smith, Robust point correspondence applied to two- and three-dimensional image registration, IEEE Transaction on Pattern Analysis and Machine Intelligence 23 (2001) 165–179.
[81] E. Gu¨lch, Results of test on image matching of ISPRS WG, ISPRS Journal of Photogrammetry and Remote Sensing 46 (1991) 1–18.
[82] J.V. Hajnal, D.L.G. Hill, D.J. Hawkes, Medical Image Registration, CRC Press, Baton Rouge, Florida, 2001, ISBN 0-8493-0064-9.
[83] H. Hanaizumi, S. Fujimura, An automated method for registration of satellite remote sensing images, Proceedings of the International Geoscience and Remote Sensing Symposium IGARSS’93, Tokyo, Japan, 1993, pp. 1348–1350.
[84] R.L. Harder, R.N. Desmarais, Interpolation using surface splines, Journal of Aircraft 9 (1972) 189–191.
[85] P. Hellier, C. Barillot, Coupling dense and landmark-based approaches for non rigid registration, IRISA research report, PI 1368:30, France, 2000.
[86] D.L.G. Hill, P.G. Batchelor, M. Holden, D.J. Hawkes, Medical image registration, Physics in Medicine and Biology 46 (2001) R1–R45.
[87] M. Holden, D.L.G. Hill, E.R.E. Denton, J.M. Jarosz, T.C.S. Cox, T.
Rohlfing, J. Goodey, D.J. Hawkes, Voxel similarity measures for 3d serial mr brain image registration, IEEE Transactions on Medical Imaging 19 (2000) 94–102.
[88] M. Holm, Towards automatic rectification of satellite images using feature based matching, Proceedings of the International Geoscience and Remote Sensing Symposium IGARSS’91, Espoo, Finland, 1991, pp. 2439–2442.
[89] H.S. Hou, H.C. Andrews, Cubic splines for image interpolation and digital filtering, IEEE Transactions on Acoustic, Speech and Signal Processing 26 (1978) 508–517.
[90] J.W. Hsieh, H.Y.M. Liao, K.C. Fan, M.T. Ko, A fast algorithm for image registration without predetermining correspondence, Proceedings of the International Conference on Pattern Recognition ICPR’96, Vienna, Austria, 1996, pp. 765–769.
[91] J.W. Hsieh, H.Y.M. Liao, K.C. Fan, M.T. Ko, Y.P. Hung, Image registration using a new edge-based approach, Computer Vision and Image Understanding 67 (1997) 112–130.
[92] Y.C. Hsieh, D.M. McKeown, F.P. Perlant, Performance evaluation of scene registration and stereo matching for cartographic feature extraction, IEEE Transactions on Pattern Analysis and Machine Intelligence 14 (1992) 214–237.
[93] M.K. Hu, Visual pattern recognition by moment invariants, IRE Transactions on Information Theory 8 (1962) 179–187.
[94] R.B. Huseby, O.M. Halck, R. Solberg, A model-based approach for geometrical correction of optical satellite images, Proceedings of the International Geoscience Remote Sensing Symposium IGARSS’99, Hamburg, Germany, 1999, pp. 330–332.
[95] D.P. Huttenlocher, G.A. Klanderman, W.J. Rucklidge, Comparing images using the Hausdorff distance, IEEE Transactions on Pattern Analysis and Machine Intellinence 15 (1993) 850–863.
[96] Numerical Recipes in C, The art of scientific computing, http://www.
nr.com.
[97] M. Jenkinson, S. Smith, A global optimisation method for robust affine registration of brain images, Medical Image Analysis 5 (2001) 143–156.
[98] S. Kaneko, I. Murase, S. Igarashi, Robust image registration by increment sign correlation, Pattern Recognition 35 (2002) 2223–2234.
[99] S. Kaneko, Y. Satoh, S. Igarashi, Using selective correlation coefficient for robust image registration, Pattern Recognition 36 (2003) 1165–1173.
[100] R.G. Keys, Cubic convolution interpolation for digital image processing, IEEE Transactions on Acoustics, Speech and Signal Processing 29 (1981) 1153–1160.
[101] L. Kitchen, A. Rosenfeld, Gray-level corner detection, Pattern Recognition Letters 1 (1982) 95–102.
[102] R. Kumar, H.S. Sawhney, J.C. Asmuth, A. Pope, S. Hsu, Registration of video to geo-referenced imagery, Proceedings of the International Conference on Pattern Recognition ICPR’98, Brisbane, Australia, 1998, pp. 1393–1399.
[103] J. Kybic, P. The´venaz, M. Unser, Multiresolution spline warping for EPI registration, Proceedings of the SPIE: Mathematical ImagingWavelet Applications in Signal and Image Processing, Denver, Colorado, 1999, pp. 571–579.
[104] D. Lavine, B. Lambird, L. Kanal, Recognition of spatial point patterns, Pattern Recognition 16 (1983) 289–295.
[105] J. le Moigne, Parallel registratin of multi-sensor remotely sensed imagery using wavelet coefficients, Proceedings of the SPIE: Wavelet Applications, Orlando, Florida, 2242, 1994, pp. 432–443.
[106] J. le Moigne, First evaluation of automatic image registration methods, Proceedings of the International Geoscience and Remote Sensing Symposium IGARSS’98, Seattle, Washington, 1998, pp.
315–317.
[107] T.M. Lehmann, A two stage algorithm for model-based registration of medical images, Proceedings of the Interantional Conference on Pattern Recognition ICPR’98, Brisbane, Australia, 1998, pp. 344– 352.
[108] T.M. Lehmann, C. Go¨nner, K. Spitzer, Addendum: B-spline interpolation in medical image processing, IEEE Transaction on Medical Imaging 20 (2001) 660–665.
[109] T.M. Lehmann, C. G¨ onner, K. Spitzer, Survey: interpolation methods in medical image processing, IEEE Transactions on Medical Imaging 18 (1999) 1049–1075.
[110] H. Lester, S.R. Arridge, Summarising fluid registration by thin-plate spline warps with many landmarks, In Proceedings of Medical Image Understanding and Analysis (MIUA97), Oxford, 1997.
[111] H. Lester, S.R. Arridge, A survey of hierarchical non-linear medical image registration, Pattern Recognition 32 (1999) 129–149.
[112] H. Li, B.S. Manjunath, S.K. Mitra, A contour-based approach to multisensor image registration, IEEE Transactions on Image Processing 4 (1995) 320–334.
[113] S.Z. Li, Matching: Invariant to translations, rotations and scale changes, Pattern Recognition 25 (1992) 583–594.
[114] S.Z. Li, J. Kittler, M. Petrou, Matching and recognition of road networks from aerial images, Proceedings of the Second European Conference on Computer Vision ECCV’92, St Margherita, Italy, 1992, pp. 857–861.
[115] B. Likar, F. Pernus, Automatic extraction of corresponding points for the registration of medical images, Medical Physics 26 (1999) 1678–1686.
[116] B. Likar, F. Pernus, A hierarchical approach to elastic registration based on mutual information, Image and Vision Computing 19 (2001) 33–44.
[117] J.A. Little, D.L.G. Hill, D.J. Hawkes, Deformations incorporating rigid structures, Computer Vision and Image Understanding 66 (1997) 223–232.
[118] J. Liu, B.C. Vemuri, J.L. Marroquin, Local frequency representations for robust multimodal image registration, IEEE Transactions on Medical Imaging 21 (2002) 462–469.
[119] L. Lucchese, G. Doretto, G.M. Cortelazzo, A frequency domain technique for range data registration, IEEE Transactions on Pattern Analysis and Machine Intelligence 24 (2002) 1468–1484.
[120] F. Maes, A. Collignon, D. Vandermeulen, G. Marchal, P. Suetens, Multimodality image registration by maximization of mutual information, IEEE Transactions on Medical Imaging 16 (1997) 187–198.
[121] J.B.A. Maintz, P.A. van den Elsen, M.A. Viergever, Comparison of edge-based and ridge-based registration of CT and MR brain images, Medical Image Analysis 1 (1996) 151–161.
[122] J.B.A. Maintz, P.A. van den Elsen, M.A. Viergever, Evaluation on ridge seeking operators for multimodality medical image matching, IEEE Transactions on Pattern Analysis and Machine Intelligence 18 (1996) 353–365.
[123] J.B.A. Maintz, M.A. Viergever, A survey of medical image registration, Medical Image Analysis 2 (1998) 1–36.
[124] H. Maitre, Y. Wu, Improving dynamic programming to solve image registration, Pattern Recognition 20 (1987) 443–462.
[125] B.S. Manjunath, C. Shekhar, R. Chellapa, A new approach to image feature detection with applications, Pattern Recognition 29 (1996) 627–640.
[126] D. Marr, E. Hildreth, Theory of edge detection, Proceedings of the Royal Society of London, B 207 (1980) 187–217.
[127] J. Matas, S ˇ . Obdrzˇa´lek, O. Chum, Local affine frames for widebaseline stereo, in: R. Kasturi, D. Laurendeau, C. Suen (Eds.), 16th International Conference on Pattern Recognition ICPR 2002, vol. 4, 2002, pp. 363–366.
[128] G. Medioni, R. Nevatia, Matching images using linear features, IEEE Transactions on Pattern Analysis and Machine Intellingence 6 (1984) 675–685.
[129] E.H.W. Meijering, K.J. Zuiderveld, M.A. Viergever, Image reconstruction by convolution with symmetrical piecewise nthorder polynomial kernels, IEEE Transactions on Image Processing 8 (1999) 192–201.
[130] R.S. Mitra, N.N. Murthy, Elastic maximal matching, Pattern Recognition 24 (1991) 747–753.
[131] P. Montesinos, V. Gouet, R. Deriche, D. Pele´, Matching color uncalibrated images using differential invariants, Image and Vision Computing 18 (2000) 659–671.
[132] S. Moss, E.R. Hancock, Multiple line-template matching with EM algorithm, Pattern Recognition Letters 18 (1997) 1283–1292.
[133] F. Murtagh, A feature based OðN2Þ approach to point pattern matching, Proceedings of the Internatinal Confernce on Pattern Recognition ICPR’92, Hague, The Netherlands, 1992, pp. 174– 177.
[134] S.J. Nelson, M.R. Day, P. Buffone, L.L. Wald, T.F. Budinger, R.
Hawkins, W. Dillon, S. Huhn, M. Prados, S. Chang, D.B. Vigneron, Alignment of volume mri and high resolution f-18 flurodeoxyglucose pet images for evaluation of patients with brain tumors, Journal of Computed Assisted Tomography 21 (1997) 183–191.
[135] A. Noble, Finding corners, Image and Vision Computing 6 (1988) 121–128.
[136] H. Ogawa, Labeled point pattern matching by fuzzy relaxation, Pattern Recognition 17 (1984) 569–573.
[137] N.R. Pal, S.K. Pal, A review on image segmentation techniques, Pattern Recognition 26 (1993) 1277–1294.
[138] J.A. Parker, R.V. Kenyon, D.E. Troxel, Comparison of interpolating methods for image resampling, IEEE Transactions on Medical Imaging 2 (1983) 31–39.
[139] E.I. Parsai, K.M. Ayyangar, R.R. Dobelbower, J.A. Siegel, Clinical fusion of three-dimensional images using bremsstrahlung spect and ct, Journal of Nuclear Medicine 38 (1997) 319–324.
[140] W. Peckar, C. Schnorr, K. Rohr, H.S. Stiehl, Two step parameterfree elastic image registration with prescribed point displacements, Journal of Mathematical Imaging and Vision 10 (1999) 143–162.
[141] T. Peli, An algorithm for recognition and localization of rotated and scaled objects, Proceedings of the IEEE 69 (1981) 483–485.
[142] G.P. Penney, J. Weese, J.A. Little, P. Desmedt, D.L.G. Hill, D.J.
Hawkes, A comparison of similarity measures for use in 2D–3D medical image registration, IEEE Transactions on Medical Imaging 17 (1998) 586–595.
[143] J.P.W. Pluim, J.B.A. Maintz, M.A. Viergever, Mutual information matching in multiresolution contexts, Image and Vision Computing 19 (2001) 45–52.
[144] M.J.D. Powell, Tabulation of thin plate splines on a very fine twodimensional grid, Numerical Analysis Report of University of Cambridge, DAMTP/1992/NA2, Cambridge, UK, 1992.
[145] W.K. Pratt, Correlation techniques of image registration, IEEE Transactions on Aerospace and Electronic Systems 10 (1974) 353–358.
[146] W.K. Pratt, Digital Image Processing, 2nd ed., Wiley, New York, 1991.
[147] K.E. Price, Relaxation matching techniques—a comparison, IEEE Transactions on Pattern Analysis and Machine Intellingence 7 (1985) 617–623.
[148] S. Ranade, A. Rosenfeld, Point pattern matching by relaxation, Pattern Recognition 12 (1980) 269–275.
[149] A. Rangarajan, H. Chui, J.S. Duncan, Rigid point feature registration using mutual information, Medical Image Analysis 4 (1999) 1–17.
[150] B.S. Reddy, B.N. Chatterji, An FFT-based technique for translation, rotation and scale-invariant image registration, IEEE Transactions on Image Processing 5 (1996) 1266–1271.
[151] B. Rezaie, M.D. Srinath, Algorithms for fast image registration, IEEE Transactions on Aerospace and Electronic Systems 20 (1984) 716–728.
[152] N. Ritter, R. Owens, J. Cooper, R.H. Eikelboom, P.P. van Saarloos, Registration of stereo and temporal images of the retina, IEEE Transactions on Medical Imaging 18 (1999) 404–418.
[153] A. Roche, G. Malandain, N. Ayache, Unifying maximum likelihood approaches in medical image registration, International Journal of Imaging Systems and Technology 11 (2000) 71–80.
[154] A. Roche, G. Malandain, X. Pennec, N. Ayache, The correlation ratio as a new similarity measure for multimodal image registration, Proceedings of the First International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI’98), Lecture Notes in Computer Science, Cambridge, USA, vol. 1496, 1998, pp. 1115–1124.
[155] K. Rohr, Localization properties of direct corner detectors, Journal of Mathematical Imaging and Vision 4 (1994) 139–150.
[156] K. Rohr, Landmark-Based Image Analysis: Using Geometric and Intensity Models, Computational Imaging and Vision Series, vol. 21, Kluwer Academic Publishers, Dordrecht, 2001.
[157] K. Rohr, H.S. Stiehl, T.M. Buzug, J. Weese, M.H. Kuhn, Landmarkbased elastic registration using approximating thin-plate splines, IEEE Transactions on Medical Imaging 20 (2001) 526–534.
[158] K. Rohr, H.S. Stiehl, R. Sprengel, W. Beil, T.M. Buzug, J. Wees, M.H. Kuhn, Point based elastic registration of medical image data using approximating thin-plate splines, Proceedings of the Visualization in Biomedical Computing VBC’96, Hamburg, Germany, 1996, pp. 297–306.
[159] K. Rohr, H.S. Stiehl, R. Sprengel, W. Beil, T.M. Buzug, J. Weese, M.H. Kuhn, Nonrigid registration of medical images based on anatomical point landmarks and approximating thin-plate splines, Proceedings of the Aacheren Workshop: Bildverarbeiterung fu¨ r die Medizin, Aachen, Germany, 1996, pp. 41–46.
[160] A. Rosenfeld, G.J. Vanderbrug, Coarse–fine template matching, IEEE Transactions on Systems, Man and Cybernetics 7 (1977) 104–107.
[161] M. Roux, Automatic registration of SPOT images and digitized maps, Proceedings of the IEEE International Conference on Image Processing ICIP’96, Lausanne, Switzerland, 1996, pp. 625–628.
[162] D. Rueckert, C. Hayes, C. Studholme, P. Summers, M. Leach, D.J.
Hawkes, Non-rigid registration of breast MR images using mutual information, Proceedings of the Medical Image Computing and Computer-Assisted Intervention MICCAI’98, Cambridge, Massachusetts, 1998, pp. 1144–1152.
[163] J. Sato, R. Cipolla, Image registration using multi-scale texture moments, Image and Vision Computing 13 (1995) 341–353.
[164] H.S. Sawhney, R. Kumar, True multi-image alignment and its applications to mosaicing and lens distortion correction, IEEE Transactions on Pattern Analysis and Machine Intellingece 21 (1999) 235–243.
[165] M. Sester, H. Hild, D. Fritsch, Definition of ground control features for image registration using GIS data, Proceedings of the Symposium on Object Recognition and Scene Classification from Multispectral and Multisensor Pixels, CD-ROM, Columbus, Ohio, 1998, 7 pp.
[166] R.K. Sharma, M. Pavel, Multisensor image registration, Proceedings of the Society for Information Display XXVIII (1997) 951–954.
[167] C. Shekhar, V. Govindu, R. Chellapa, Multisensor image registration by feature consensus, Pattern Recognition 32 (1999) 39–52.
[168] D. Shin, J.K. Pollard, J.P. Muller, Accurate geometric correction of ATSR images, IEEE Transactions on Geoscience and Remote Sensing 35 (1997) 997–1006.
[169] Y. Shinagawa, T.L. Kunii, Unconstrained automatic image matching using multiresolutional critical-point filters, IEEE Transactions on Pattern Analysis and Machine Intelligence 20 (1998) 994–1010.
[170] A. Simper, Correcting general band-to-band misregistrations, Proceedings of the IEEE International Conference on Image Processing ICIP’96, Lausanne, Switzerland, 1996, 2, pp. 597–600.
[171] D. Skea, I. Barrodale, R. Kuwahara, R. Poeckert, A control point matching algorithm, Pattern Recognition 26 (1993) 269–276.
[172] S.M. Smith, SUSAN low level image processing, http://www.fmrib.
ox.ac.uk/~spacesteve/susan.
[173] S.M. Smith, J.M. Brady, SUSAN—a new approach to low level image processing, International Journal of Computer Vision 23 (1997) 45–78.
[174] J.P.P. Starink, E. Baker, Finding point correspondence using simulated annealing, Pattern Recognition 28 (1995) 231–240.
[175] G. Stockman, S. Kopstein, S. Benett, Matching images to models for registration and object detection via clustering, IEEE Transactions on Pattern Analysis and Machine Intelligence 4 (1982) 229–241.
[176] H.S. Stone, J. le Moigne, M. McGuire, The translation sensitivity of wavelet-based registration, IEEE Transactions on Pattern Analysis and Machine Intelligence 21 (1999) 1074–1081.
[177] C. Studholme, D.L.G. Hill, D.J. Hawkes, An overlap invariant entropy measure of 3D medical image alignment, Pattern Recognition 32 (1999) 71–86.
[178] T. Suk, J. Flusser, Vertex-based features for recognition of projectively deformed polygons, Pattern Recognition 29 (1996) 361–367.
[179] T. Suk, J. Flusser, Point-based projective invariants, Pattern Recognition 33 (2000) 251–261.
[180] A. Taza, C.Y. Suen, Description of planar shapes using shape matrices, IEEE Transactions on Systems, Man, and Cybernetics 19 (1989) 1281–1289.
[181] O. Thepaut, K. Kpalma, J. Ronsin, Automatic registration of ERS and SPOT multisensor images in a data fusion context, Forest Ecology and Management 128 (2000) 93–100.
[182] P. The´venaz, T. Blu, M. Unser, Image interpolation and resampling, Handbook of Medical Image Processing, Academic Press, New York, 2003, in press.
[183] P. The´venaz, T. Blu, M. Unser, Interpolation revisited, IEEE Transactions on Medical Imaging 19 (2000) 739–758.
[184] P. The´venaz, U.E. Ruttimann, M. Unser, A pyramidal approach to subpixel registration based on intensity, IEEE Transactions on Image Processing 7 (1998) 27–41.
[185] P. The´venaz, U.E. Ruttimann, M. Unser, Iterative multiscale registration without landmarks, Proceedings of the IEEE International Confernece on Image Processing ICIP’95, Washington DC, 1995, pp. 228–231.
[186] P. The´venaz, M. Unser, An efficient mutual information optimizer for multiresolution image registration, Proceedings of the IEEE International Conference on Image Processing ICIP’98, Chicago, IL, 1998, pp. 833–837.
[187] P. The´venaz, M. Unser, A pyramid approach to sub-pixel image fusion based on mutual information, Proceedings of the IEEE Interantional Conference on Image Processing ICIP’96, Lausanne, Switzerland, 1996, pp. 265–268.
[188] P. The´venaz, M. Unser, Spline pyramids for inter-modal image registration using mutual information, Proceedings of SPIE: Wavelet Applications in Signal and Image Processing, San Diego, CA, 1997, pp. 236–247.
[189] J.-P. Thirion, Image matching as a diffusion process: an analogy with Maxwell’s demons, Medical Image Analysis 2 (1998) 243–260.
[190] J. Ton, A.K. Jain, Registering landsat images by point matching, IEEE Transactions on Geoscience and Remote Sensing 27 (1989) 642–651.
[191] K. Toraichi, S. Yang, R. Mori, Two-dimensional spline interpolation for image reconstruction, Pattern Recognition 21 (1988) 275–284.
[192] M. Trajkovic, M. Hedley, Fast corner detection, Image and Vision Computing 16 (1998) 75–87.
[193] R. Turcajova´, J. Kautsky, A hierarchical multiresolution technique for image registration, Proceedings of SPIE Mathematical Imaging: Wavelet Applications in Signal and Image Processing, Colorado, 1996.
[194] T. Tuytelaars, L.V. Gool, Matching widely separated views based on affinely invariant neighbourhoods, International Journal of Computer Vision (2003) to appear.
[195] P.A. van den Elsen, E.-J.D. Pol, M.A. Viergever, Medical image matching-a review with classification, IEEE Engineering in Medicine and Biology 12 (1993) 26–39.
[196] P. van Wie, M. Stein, A landsat digital image rectification system, IEEE Transactions on Geoscience Electronics 15 (1977) 130–136.
[197] G.J. Vanderbrug, A. Rosenfeld, Two stage template matching, IEEE Transactions on Computers 26 (1977) 384–393.
[198] A.S. Vasileisky, B. Zhukov, M. Berger, Automated image coregistration based on linear feature recognition, Proceedings of the Second Conference Fusion of Earth Data, Sophia Antipolis, France, 1998, pp. 59–66.
[199] B.C. Vemuri, J. Ye, Y. Chen, C.M. Leonard, Image registration via level-set motion: Applications to atlas-based segmentation, Medical Image Analysis 7 (2003) 1–20.
[200] A.D. Ventura, A. Rampini, R. Schettini, Image registration by recognition of corresponding structures, IEEE Transactions on Geoscience and Remote Sensing 28 (1990) 305–314.
[201] P. Viola, W.M. Wells, Alignment by maximization of mutual information, International Journal of Computer Vision 24 (1997) 137–154.
[202] N. Vujovic, D. Brzakovic, Establishing the correspondence between control points in pairs of mammographic images, IEEE Transactions on Image Processing 6 (1997) 1388–1399.
[203] G. Wahba, Spline Models for Observational Data, SIAM, Philadelphia, 1990.
[204] C.Y. Wang, H. Sun, S. Yadas, A. Rosenfeld, Some experiments in relaxation image matching using corner features, Pattern Recognition 16 (1983) 167–182.
[205] W.H. Wang, Y.C. Chen, Image registration by control points pairing using the invariant properties of line segments, Pattern Recognition Letters 18 (1997) 269–281.
[206] J. West, J.M. Fitzpatrik, M.Y. Wang, B.M. Dawant Jr., C.R. Maurer, R.M. Kessler, R.J. Maciunas, Retrospective intermodality registration techniques for images of the head: surface-based versus volume-based, IEEE Transactions on Medical Imaging 18 (1999) 144–150.
[207] J. West, et al., Comparison and evaluation of retrospective intermodality brain image registration techniques, Journal of Computer Assisted Tomography 21 (1997) 554–566.
[208] A.P. Whichello, H. Yan, Document image mosaicing, Proceedings of the International Conference on Pattern Recognition ICPR’98, Brisbane, Australia, 1998, pp. 1081–1084.
[209] R. Wiemker, K. Rohr, L. Binder, R. Sprengel, H.S. Stiehl, Application of elastic registration to imaginery from airborne scanners, International Archives for Photogrammetry and Remote Sensing XXXI-B4 (1996) 949–954.
[210] G. Wolberg, S. Zokai, Robust image registration using log-polar transform, Proceedings of the IEEE International Conference on Image Processing, Canada, September 2000.
[211] G. Wolberg, S. Zokai, Image registration for perspective deformation recovery, SPIE Conference on Automatic Target Recognition X, Orlando, Florida, USA, April 2000, p. 12.
[212] G. Wollny, F. Kruggel, Computational cost of nonrigid registration algorithms based on fluid dynamics, IEEE Transactions on Medical Imaging 21 (2002) 946–952.
[213] R.Y. Wong, E.L. Hall, Scene matching with invariant moments, Computer Graphics and Image Processing 8 (1978) 16–24.
[214] R.Y. Wong, E.L. Hall, Sequential hierarchical scene matching, IEEE Transactions on Computers 27 (1978) 359–366.
[215] R.P. Woods, S.T. Grafton, C.J. Holmes, S.R. Cherry, J.C. Mazziotta, Automated image registration: I. General methods and intrasubject, intramodality validation, Journal of Computer Assisted Tomography 22 (1998) 141–154.
[216] Z. Yang, F.S. Cohen, Image registration and object recognition using affine invariants and convex hulls, IEEE Transactions on Image Processing 8 (1999) 934–946.
[217] Y. You, M. Kaveh, A regularization approach to joint blur identification and image restoration, IEEE Transactions on Image Processing 5 (1996) 416–428.
[218] F. Zana, J.C. Klein, A multimodal registration algorithm of eye fundus images using vessels detection and Hough transform, IEEE Transactions on Medical Imaging 18 (1999) 419–428.
[219] Q. Zheng, R. Chellapa, A computational vision approach to image registration, IEEE Transactions on Image Processing 2 (1993) 311–325.
[220] Z. Zheng, H. Wang, E.K. Teoh, Analysis of gray level corner detection, Pattern Recognition Letters 20 (1999) 149–162.
[221] Y.M. Zhu, Volume image registration by cross-entropy optimization, IEEE Transactions on Medical Imaging 21 (2002) 174–180.
[222] D. Ziou, S. Tabbone, Edge detection techniques—an overview, http://citeseer.nj.nec.com/ziou97edge.html, 1997.
[223] B. Zitova´, J. Flusser, F. Sroubek, Application of image processing for the conservation of the medieval mosaic, Proceedings of the IEEE International Conference on Image Processing ICIP’02, Rochester, MI, 2002, pp. 993–996.
[224] B. Zitova´, J. Kautsky, G. Peters, J. Flusser, Robust detection of significant points in multiframe images, Pattern Recognition Letters 20 (1999) 199–206.
