保姆级教程之SABO-VMD-CNN-SVM的分类诊断，特征可视化

今天出一期基于SABO-VMD-CNN-SVM的分类诊断。

依旧是采用经典的西储大学轴承数据。基本流程如下：

首先是以最小包络熵为适应度函数，采用SABO优化VMD的两个参数。其次对每种状态的数据进行特征向量的求取，并为每组数据打上标签。然后将数据送入CNN进行特征提取， 并进行PCA降维后特征可视化，并与未进行CNN特征提取的数据可视化结果进行比较。最后将CNN提取的特征送入SVM进行分类。

其他数据的故障分类都可以适用该方法！数据替换十分简单，代码注释非常详细！

友情提示：对于刚接触故障诊断的新手来说，这篇文章信息量可能有点大，大家可以收藏反复阅读。即便有些内容本篇文章没讲出来，但其中的一些跳转链接，也完全把故障诊断这个故事讲清楚了。

文件夹目录如下：都是作者精心整理过的。程序运行十分简单，按照步骤，一步步来即可！

考虑到大家可能会用到VMD的相关作图，包络谱，频谱图等，作者在这里也一并附在代码中了。这部分大家需要自行更改数据！具体可以参考这个：VMD分解，matlab代码，包络线，包络谱，中心频率，峭度值，能量熵，样本熵，模糊熵，排列熵，多尺度排列熵，西储大学数据集为例

如截图所示，本期内容一共做了三件事情：

一，对官方下载的西储大学数据进行处理

步骤如下：

①一共加载4种状态的数据，分别是正常状态，内圈故障，外圈故障，滚动体故障。②设置滑动窗口w，每个数据的故障样本点个数s，每个故障类型的样本量m。③将所有的数据滑窗完毕之后，综合到一个data变量中，也就是截图中的data_total_1797.mat

有关西储大学数据的处理之前有文章也讲过，大家可以看这篇文章：西储大学轴承诊断数据处理，matlab免费代码获取

二，对第一步数据处理得到的数据进行特征提取

选取五种适应度函数进行优化，这里大家可以自行决定选哪一个！以此确定VMD的最佳k和α参数。五种适应度函数分别是：最小包络熵，最小样本熵，最小信息熵，最小排列熵，排列熵/互信息熵，代码中可以一键切换。至于应该选择哪种作为自己的适应度函数，大家可以看这篇文章。VMD为什么需要进行参数优化，最小包络熵/样本熵/排列熵/信息熵，适应度函数到底该选哪个

至于特征提取的具体原理，也在这篇文章进行过详细介绍，大家可以跳转阅读。简单来说，就是利用包络熵最小的准则把每个样本的最佳IMF分量提取出来，然后对其9个指标进行计算，分别是：均值，方差，峰值，峭度，有效值，峰值因子，脉冲因子，波形因子，裕度因子。然后用这9个指标构建每个样本的特征向量。

另外本篇文章采用了2023年一个较新且效率较高的智能算法---减法优化器(SABO)，对VMD参数进行了优化，找到了每个故障类型的最佳IMF分量，并利用包络熵最小的准则，提取出了最佳的IMF分量。

三，采用卷积神经网络(CNN)对数据特征进行提取

这里做了对比实验。将经过CNN特征提取的向量和未经过CNN特征提取的向量可视化结果进行对比。具体做法为：采用了PCA降维后进行可视化。结果如下：

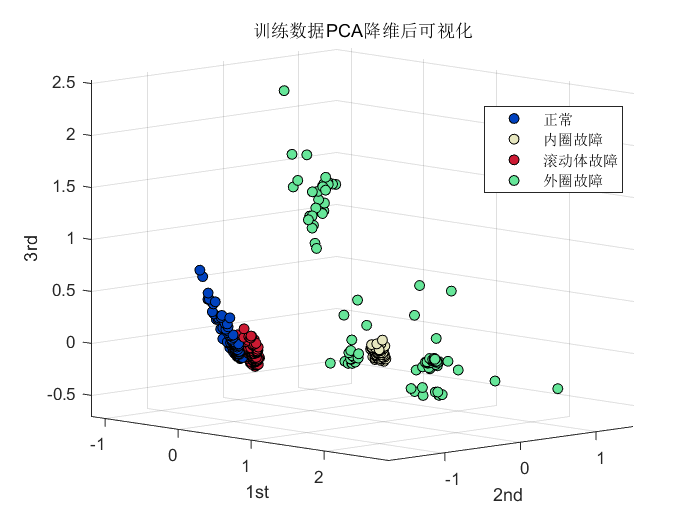
第一张图是未经CNN特征提取，直接采用PCA降维后的特征可视化结果，可以看到，正常状态和滚动体故障有严重重叠！而采用CNN提取后，第二张图可以看到，四种状态不存在重合，各个类别区分明显！证明了CNN特征提取的有效性。

五、采用支持向量机实现故障分类

将CNN提取好的特征数据送入SVM进行训练与测试。本文所选SVM是从官网下载的libsvm-3.3版本，作者已编译好，大家可以直接运行。如果想自行编译的童鞋可以从网站下载：https://www.csie.ntu.edu.tw/~cjlin/libsvm/index.html，编译步骤可以参考https://blog.csdn.net/qq_42457960/article/details/109275227

本文采用了网格搜索机制，并采用5折交叉验证，对SVM的惩罚因子c和gamma参数进行寻优。

结果展示

混淆矩阵图，有的文章会采用这种图：

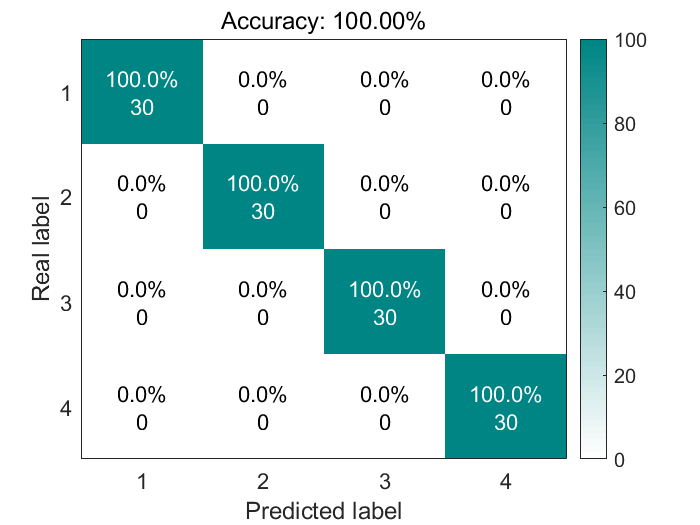
这里不得不说一句，官方给出的libSVM包，准确率就是嘎嘎高！

以上所有图片在代码包里都能复现。

有些同学可能会用到一些频谱图，包络谱图等，这里以105.mat故障信号为例进行展示：

运行文件夹“VMD分解，matlab代码，包络线，包络熵……”下的MAIN.m文件后，会出现如下运行结果：

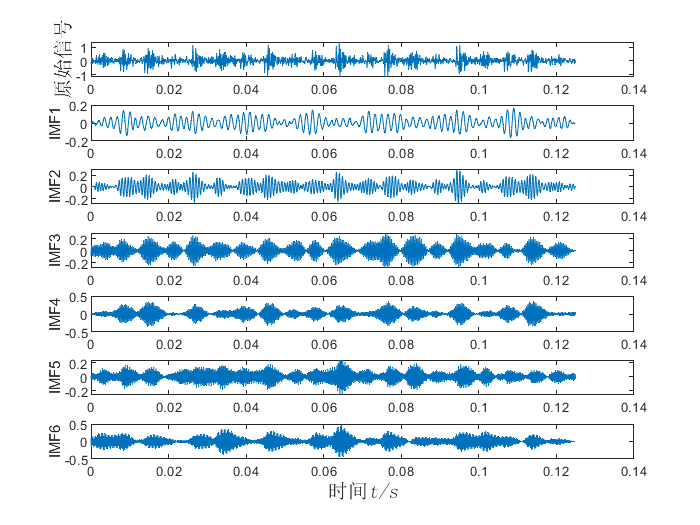
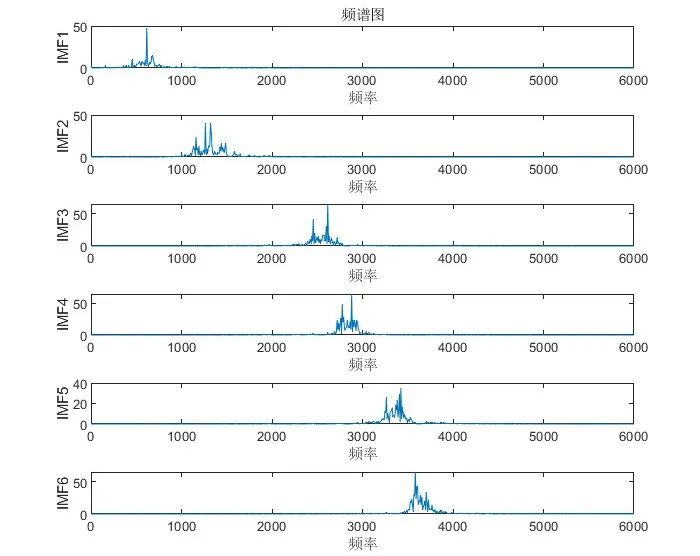
在命令窗口会出现如下计算结果：

IMF1的峭度值为：2.6102
IMF2的峭度值为：3.3346
IMF3的峭度值为：2.9038
IMF4的峭度值为：3.5663
IMF5的峭度值为：2.7648
IMF6的峭度值为：3.2977
IMF分量的能量
    4.9829   10.5892   14.4765   19.8061    8.4764   24.3339
 
 
EMD能量熵=%.4f
    0.1693    0.2632    0.3051    0.3423    0.2335    0.3600
 
 
IMF1的近似熵为：0.023426
IMF2的近似熵为：0.15115
IMF3的近似熵为：0.08722
IMF4的近似熵为：0.04402
IMF5的近似熵为：0.052554
IMF6的近似熵为：0.14538
IMF1的包络熵为：7.2053
IMF2的包络熵为：7.14
IMF3的包络熵为：7.1537
IMF4的包络熵为：7.0853
IMF5的包络熵为：7.2063
IMF6的包络熵为：7.1476
局部最小包络熵为：7.0853
IMF1的模糊熵为：0.12759
IMF2的模糊熵为：0.090684
IMF3的模糊熵为：0.041706
IMF4的模糊熵为：-0.0032906
IMF5的模糊熵为：-0.011035
IMF6的模糊熵为：0.030635
IMF1的排列熵为：0.61446
IMF2的排列熵为：0.76756
IMF3的排列熵为：0.93485
IMF4的排列熵为：0.95524
IMF5的排列熵为：0.98658
IMF6的排列熵为：0.99433
多尺度排列熵为：
0.36792     0.50757     0.56639     0.64017     0.68493     0.66705     0.69098     0.66583     0.61102     0.62604     0.62396     0.61879     0.67588     0.66087     0.67663     0.65568     0.66656     0.65949     0.63769     0.63972     0.63041     0.60632     0.60124     0.58355     0.57844      0.5803     0.57774     0.55767     0.51696     0.55986
0.48773     0.66594     0.69663     0.62542     0.59005     0.72211     0.73193     0.69654      0.6619      0.6861     0.71204     0.67167     0.63684     0.64251     0.64805     0.65568     0.63513     0.65138     0.64346     0.62353     0.62084     0.58707     0.57752     0.59973     0.58993     0.55851     0.57774     0.58401     0.57735      0.5739
0.57786     0.57523     0.67386     0.65101     0.56296     0.71078     0.58023     0.71316     0.67834     0.65725     0.68971     0.64193     0.68882     0.67817     0.65194     0.64461      0.6221     0.64496     0.62037     0.62467     0.60686     0.59167     0.60124     0.59603     0.58993      0.5803     0.58617     0.58401     0.55902     0.56922
0.58138     0.47632     0.65939     0.66591     0.64333     0.65131     0.68434     0.63124     0.61944     0.67578     0.65511     0.67651     0.64736     0.66422     0.61521      0.6437     0.61607     0.63518     0.60773     0.63671     0.60246     0.58959     0.61178     0.56737     0.59376     0.58841     0.55667     0.55162     0.57277     0.57859
0.54329     0.53176       0.618     0.59543     0.66657     0.71203     0.68693     0.69594     0.56685     0.71009     0.64683     0.66333     0.67515     0.67042     0.63474     0.59895     0.66148     0.64328     0.62614      0.6337     0.63041     0.61969     0.59859     0.58864     0.59376     0.56662     0.57774     0.58401     0.57735     0.56922
0.53646     0.58339      0.5363     0.66055     0.50474     0.62548     0.65051     0.63196     0.67276      0.6993     0.67454     0.64403     0.61372     0.67611      0.5754      0.6362     0.64941     0.59124     0.63191     0.60547     0.60168     0.60632     0.61178     0.60343     0.53724     0.57877     0.59039     0.57523     0.54182     0.56922
IMF1的样本熵为：0.6129
IMF2的样本熵为：0.52726
IMF3的样本熵为：0.32156
IMF4的样本熵为：0.21892
IMF5的样本熵为：0.30553
IMF6的样本熵为：0.24375

部分代码

数据处理代码：

clc;
clear;
addpath(genpath(pwd));
%DE是驱动端数据 FE是风扇端数据 BA是加速度数据 选择其中一个就行
load 97.mat  %正常
load 105.mat  %直径0.007英寸，转速为1797时的  内圈故障
load 118.mat   %直径0.007，转速为1797时的  滚动体故障
load 130.mat  %直径0.007，转速为1797时的  外圈故障
% 一共是4个状态，每个状态有120组样本，每个样本的数据量大小为：1×2048
w=1000;                  % w是滑动窗口的大小1000
s=2048;                  % 每个故障表示有2048个故障点
m = 120;            %每种故障有120个样本
D0=[];
for i =1:m
    D0 = [D0,X097_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D0 = D0';
D1=[];
for i =1:m
    D1 = [D1,X105_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D1 = D1';

SABO优化VMD参数并特征提取的代码：

%% 以最小包络熵、最小样本熵、最小信息熵、最小排列熵，排列熵/互信息熵，为目标函数（任选其一），采用SABO算法优化VMD，求取VMD最佳的两个参数
clear
clc
close all
addpath(genpath(pwd))
xz = 1;  %xz, 选择1，以最小包络熵为适应度函数，
% 选择2，以最小样本熵为适应度函数，
% 选择3，以最小信息熵为适应度函数，
% 选择4，以最小排列熵为适应度函数，
% 选择5，以复合指标：排列熵/互信息熵为适应度函数。
if xz == 1  
    fobj=@EnvelopeEntropyCost;          %最小包络熵
elseif xz == 2
    fobj=@SampleEntropyCost;            %最小样本熵
elseif xz == 3  
    fobj=@infoEntropyCost;              %最小信息熵
elseif xz == 4
    fobj=@PermutationEntropyCost;       %最小排列熵
elseif xz == 5
    fobj=@compositeEntropyCost;       %复合指标：排列熵/互信息熵
end
load data_total_1797.mat   %这里选取转速为1797的4种故障，大家也可以选取其他类型的数据
D=2;             % 优化变量数目
lb=[100 3];      % 下限值，分别是a,k
ub=[2500 10];        % 上限值
T=20;       % 最大迭代数目
N=20;        % 种群规模
vmddata = [];%保存提取好的故障特征向量
zuijiacanshu = []; %保存每种故障状态的最佳VMD参数和对应的最佳IMF索引值
curve = [];  %保存每种故障状态对应的优化VMD收敛曲线
for i=1:4   %因为有4种故障状态
    disp(['正在对第',num2str(i),'个故障类型的数据进行VMD优化……请耐心等待！'])
    every_data = data(1+120*(i-1):120*i,:);  %一种状态是120个样本，每次选120个样本进行VMD优化和特征提取
    vmddata =  [vmddata;new_data];  %将每个状态提取得到的特征向量都放在一起
end
    save curve curve  %保存每种故障状态对应的优化VMD收敛曲线
    save zuijiacanshu zuijiacanshu  %保存每种故障状态的最佳VMD参数和对应的最佳IMF索引值
    save vmddata.mat vmddata  %将提取的特征向量保存为mat文件

---

CNN-SVM诊断的代码：

%% 初始化
clear
close all
clc
warning off
% 数据读取
addpath(genpath(pwd));
load vmddata.mat  %加载处理好的特征数据
data = vmddata;
bv = 120;    %每种状态数据有120组
%% 给数据加标签值
hhh = size(data,2);
for i=1:size(data,1)/bv
    data(1+bv*(i-1):bv*i,hhh+1)=i;
end
input=data(:,1:hhh);
output =data(:,end);
 
 
%% 划分训练集和测试集
jg = bv;   %每组120个样本
tn = 90;    %每组数据选前tn个样本进行训练，后bv-tn个进行测试
input_train = []; output_train = [];
input_test = []; output_test = [];
for i = 1:max(data(:,end))
    input_train=[input_train;input(1+jg*(i-1):jg*(i-1)+tn,:)];
    output_train=[output_train;output(1+jg*(i-1):jg*(i-1)+tn,:)];
    input_test=[input_test;input(jg*(i-1)+tn+1:i*jg,:)];
    output_test=[output_test;output(jg*(i-1)+tn+1:i*jg,:)];
end
input_train = input_train'; 
input_test = input_test';
%归一化处理
[inputn_train,inputps]=mapminmax(input_train);
[inputn_test,inputtestps]=mapminmax('apply',input_test,inputps);  inputn_test =inputn_test';
[c,g] = meshgrid(-10:0.5:10,-10:0.5:10);  %调整间距，可以搜索的更加精细
[m,n] = size(c);
cg = zeros(m,n);
eps = 10^(-4);
v = 5;  %采用5折交叉验证
bestacc = 0;

点击下方卡片获取更多代码！

往期更多故障诊断的优秀文章推荐：

保姆级教程之VMD-CNN-BILSTM轴承故障诊断，MATLAB代码

保姆级教程之ICEEMDAN-GWO-LSSVM的轴承诊断，MATLAB代码

保姆级教程之SABO-VMD-SVM的西储大学轴承诊断

保姆级教程之VMD-SABO-KELM优化核极限学习机的西储大学轴承诊断

“三高”论文完美复现！基于PSO-VMD-MCKD方法的风机轴承微弱故障诊断，实现早期微弱故障诊断，MATLAB代码实现

“三高”论文完美复现！基于EEMD奇异值熵的滚动轴承故障诊断方法，MATLAB代码实现

VMD分解，matlab代码，包络线，包络谱，中心频率，峭度值，能量熵，样本熵，模糊熵，排列熵，多尺度排列熵，西储大学数据集为例

更多代码请前往主页获取！