- 1如何实现高效数据处理?探索BI数据绑定与前端数据处理的最佳实践!
- 2windows下安装rabbitmq_windows安装rabbitmq
- 3linux xshell jdk hadoop(环境搭建) 虚拟机 安装(大数据搭建环境)
- 4nodejs、npm、webpack、vue-cli入门及使用_nodejs npm webpack vue
- 5网络网络层之(6)ICMPv4协议
- 6Kafka主从同步及leader&follower的理解_kafka的leader和follower
- 7Spring Cloud Gateway详解_spring cloud getaway作用
- 8vue和react 的简单对比_vue react
- 9git:如何做代码回滚
- 10大数据开发之kafka(完整版)_kafka详解大数据
个人LeetCode刷题记录(带题目链接及解答)持续更新_测试一百万随机数据的时间复杂度和空间复杂度代码并将其可视化
赞
踩
Leetcode 刷题
注:~【完成】代表还有一些方法没看,最后再看
一、一些需要重刷的典型题:
1、快速排序,归并排序,堆排序(递归的思想)
2、链表中的回文链表,其中的快慢指针,多看,多练
3、链表中的奇偶链表
二、注意事项
写代码经常出现的错误总结归纳:
1、for(;;)中的;经常写成,
2、true 的拼写错误
3、while 的离开循环条件忘写,陷入死循环
4、return忘写
5、不能使用关键字命名变量
6、链表的遍历用while,数组的遍历用for
7、C++负数不支持移位运算符
- 1
- 2
- 3
- 4
- 5
- 6
- 7
一些程序的写法:
1、vector排序的写法: Arrays.sort(nums); sort(nums.begin(),nums.end()); 2、int与string的互相转换: int a; string s; s = to_string(a); a = stoi(s); 3、注意(n&(n-1))==0外面的括号不能删 4、return n > 0 && (n & (n - 1)) == 0 && (n & 0xaaaaaaaa) == 0 排除 n<=0 的情况,**易错点**,顺序不能写错,因为是按照写的顺序依次判断条件是否成立的 5、for(int num:nums){ num=1; }//采用这种方式无法改变数组中的值 6、reverse(a.begin(),a.end())//翻转数组或者string 7、temp.resize((int)nums.size(), 0);//重新定义字符串的长度
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
三、算法思想
1、双指针(7题)
【完成】167.两数之和 II - 输入有序数组 简单
第一代代码(自己想到的)
//存在一个问题,当输入数组只有两个元素时就会出错 class Solution { public: vector<int> twoSum(vector<int>& numbers, int target) { int n=(int)numbers.size(); int mid=target/2; int i,j,pivot; vector<int> ret = {0,0}; for(i=0;i<n && numbers[i]<=mid;i++){ if(numbers[i+1]>=mid) pivot=i; } for(i=0;i<=pivot;i++){ int left=numbers[i]; for(j=pivot+1;j<n;j++){ int right=numbers[j]; if(left+right==target){ ret[0]=i+1; ret[1]=j+1; } } } return ret; } }; //改进后 [12344567]8这个实例会出错,这个是错误代码 class Solution { public: vector<int> twoSum(vector<int>& numbers, int target) { int n=(int)numbers.size(); vector<int> ret = {0,0}; if(n==2){ ret[0]=1; ret[1]=2; return ret; } int mid=target/2; int i,j,pivot; for(i=0;i<n;i++){ if(numbers[i]<=mid && numbers[i+1]>=mid){ pivot=i; break; } } for(i=0;i<=pivot;i++){ int left=numbers[i]; for(j=pivot+1;j<n;j++){ int right=numbers[j]; if(left+right==target){ ret[0]=i+1; ret[1]=j+1; } } } return ret; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
第二代代码(二分查找法)
//Leetcode 官方解答 class Solution { public: vector<int> twoSum(vector<int>& numbers, int target) { for (int i = 0; i < numbers.size(); ++i) {//每次固定一个i,然后通过二分查找法去找另一个数 int low = i + 1, high = numbers.size() - 1;//此处有双指针,low,high,用于限定除了numbers[i]的另一个数的搜索范围 while (low <= high) { int mid = (high - low) / 2 + low;//这个本质就是求中点的公式,(high+low)/2 if (numbers[mid] == target - numbers[i]) { return {i + 1, mid + 1}; } else if (numbers[mid] > target - numbers[i]) { high = mid - 1;//缩小一般的搜索范围 } else { low = mid + 1; } } } return {-1, -1}; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
第三代代码(双指针法)
//双指针法 class Solution { public: vector<int> twoSum(vector<int>& numbers, int target) { int left, right; int n=(int)numbers.size(); vector<int> ret={0,0}; for(left=0,right=n-1;left<right;){ if(numbers[left]+numbers[right]<target) left++; else if(numbers[left]+numbers[right]>target) right--; else{ ret[0]=left+1; ret[1]=right+1; break; } } return ret; } }; //Leetcode 官方解答 class Solution { public: vector<int> twoSum(vector<int>& numbers, int target) { int low = 0, high = numbers.size() - 1; while (low < high) { int sum = numbers[low] + numbers[high]; if (sum == target) { return {low + 1, high + 1};//注意这种写法 } else if (sum < target) { ++low; } else { --high; } } return {-1, -1};//注意这种写法,表示程序出错,返回错误 } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
第四代代码(哈希表法)
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
unordered_map<int,int> hashtable;
for(int i=0;i<numbers.size();i++){
auto t=hashtable.find(target-numbers[i]);
if(t!=hashtable.end()){
return {++t->second,++i};
}
hashtable[numbers[i]]=i;//注意哈希表的赋值方式
}
return {};
}
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
还有穷举法(省略)
【完成】633. 平方数之和 中等
第一代代码(双指针法)
//注意使用 long class Solution { public: bool judgeSquareSum(int c) { long r=(int)sqrt(c); long l=0; while(l<=r){ long result=l*l+r*r; if(result==c) return true; else if(result>c) r--; else l++; } return false; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
【完成】345. 反转字符串中的元音字母 简单
第一代代码
class Solution { public: bool decide(char c){ return c == 'a' || c == 'o' || c == 'e' || c == 'i' || c == 'u' || c == 'A' || c == 'O' || c == 'E' || c == 'I' || c == 'U'; } string reverseVowels(string s) { int left,right; left=0; right=s.length()-1; while(left<right){ while(left<right&&!decide(s[left])){left++;}//一开始这里的判断条件中少了left<right&& 因此left后面可能会不满足这个条件,所以出错 while(left<right&&!decide(s[right])){right--;} char temp=s[left]; s[left]=s[right]; s[right]=temp; left++; right--; } return s; } }; //融合了别人的代码 class Solution { public: bool decide(char c){ return c == 'a' || c == 'o' || c == 'e' || c == 'i' || c == 'u' || c == 'A' || c == 'O' || c == 'E' || c == 'I' || c == 'U'; } string reverseVowels(string s) { int left,right; left=0; right=s.length()-1; while(left<right){ if(!decide(s[left])){ left++; continue; } else if(!decide(s[right])){ right--; continue; } // while(!decide(s[left])){left++;continue;} // while(!decide(s[right])){right--;continue;} else{ char temp=s[left]; s[left]=s[right]; s[right]=temp; } left++; right--; } return s; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
注意这种写法中对于 string s 中是否存在某个元素的写法 ss.find(s[i]) == ss.end()
class Solution {private: unordered_set<char> ss{'a','e','i','o','u','A','E','I','O','U'};public: string reverseVowels(string s) { int i = 0; int j = s.size() - 1; while (i < j) { while (i < j && ss.find(s[i]) == ss.end()) { ++i; } while (i < j && ss.find(s[j]) == ss.end()) { --j; } if (i < j) { swap(s[i], s[j]); ++i; --j; } } return s; }};
- 1
680. 验证回文字符串 Ⅱ 中等
88. 合并两个有序数组 简单
141. 环形链表 简单
524. 通过删除字母匹配到字典里最长单词 中等
2、排序(4题)
【完成】快速选择
用于求解 Kth Element 问题,也就是第 K 个元素的问题。
可以使用快速排序的 partition() 进行实现。需要先打乱数组,否则最坏情况下时间复杂度为 O(N2)。
【完成】堆
用于求解 TopK Elements 问题,也就是 K 个最小元素的问题。使用最小堆来实现 TopK 问题,最小堆使用大顶堆来实现,大顶堆的堆顶元素为当前堆的最大元素。实现过程:不断地往大顶堆中插入新元素,当堆中元素的数量大于 k 时,移除堆顶元素,也就是当前堆中最大的元素,剩下的元素都为当前添加过的元素中最小的 K 个元素。插入和移除堆顶元素的时间复杂度都为 log2N。
堆也可以用于求解 Kth Element 问题,得到了大小为 K 的最小堆之后,因为使用了大顶堆来实现,因此堆顶元素就是第 K 大的元素。
快速选择也可以求解 TopK Elements 问题,因为找到 Kth Element 之后,再遍历一次数组,所有小于等于 Kth Element 的元素都是 TopK Elements。
可以看到,快速选择和堆排序都可以求解 Kth Element 和 TopK Elements 问题。
【完成】1. Kth Element
桶排序
【遇到问题!】1. 出现频率最多的 k 个元素
2. 按照字符出现次数对字符串排序
【完成】荷兰国旗问题
荷兰国旗包含三种颜色:红、白、蓝。
有三种颜色的球,算法的目标是将这三种球按颜色顺序正确地排列。它其实是三向切分快速排序的一种变种,在三向切分快速排序中,每次切分都将数组分成三个区间:小于切分元素、等于切分元素、大于切分元素,而该算法是将数组分成三个区间:等于红色、等于白色、等于蓝色。
1. 按颜色进行排序
75. 颜色分类 简单
单指针法
class Solution {public: void sortColors(vector<int>& nums) { int n = nums.size(); int ptr = 0; for (int i = 0; i < n; ++i) { if (nums[i] == 0) { swap(nums[i], nums[ptr]); ++ptr; } } for (int i = ptr; i < n; ++i) { if (nums[i] == 1) { swap(nums[i], nums[ptr]); ++ptr; } } }};作者:LeetCode-Solution链接:https://leetcode-cn.com/problems/sort-colors/solution/yan-se-fen-lei-by-leetcode-solution/来源:力扣(LeetCode)著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
- 1
【patition法】 (注意while和if的顺序不能颠倒)
class Solution {public: void sortColors(vector<int>& nums) { int n=nums.size(); int p0=0,p2=n-1; for(int i=0;i <= p2;i++){ while(nums[i]==2&&i <= p2){//而数组末端的情况我 们是不知道的,所以就需要用while,防止换过来的也是2 swap(nums[i],nums[p2]); p2--; } if (nums[i] == 0) {//因为i是从左边开始遍历的,所以遍历过的地方一定没有0,不存在交换nums[p0]和nums[i]之后nums[i]还是等于0的情况 swap(nums[i], nums[p0]); ++p0; } } }};
- 1
3、贪心思想(11题)
保证每次操作都是局部最优的,并且最后得到的结果是全局最优的。
【完成】1. 分配饼干
455. 分发饼干 简单
排序+贪心
class Solution {public://双指针法 int findContentChildren(vector<int>& g, vector<int>& s) { int ng=g.size(); int ns=s.size(); sort(g.begin(),g.end());//排序 sort(s.begin(),s.end()); int i=0,j=0,c=0; while(i<ng&&j<ns){ if(s[j]>=g[i]){ i++; j++; c++; } else j++; } return c; }};
- 1
2. 不重叠的区间个数
435. 无重叠区间 中等
【完成】3. 投飞镖刺破气球
452. 用最少数量的箭引爆气球 中等


蓝色荧光笔的字可以这么去理解:如果将该箭移到该箭可以射爆的气球中最左的右边界后不能射爆其他的气球的话,那这支箭在移动前也不能射爆那些气球。
知识点回顾:
lambda表达式
语法形式:[函数对象参数] (操作符重载函数参数) mutable 或 exception 声明 -> 返回值类型 {函数体}
class Solution {public: int findMinArrowShots(vector<vector<int>>& points) {// vector<vector<int>>& points 代表每个 vector<int> 容器中都有两个元素,每个两个元素的 vector 容器又被存储到外层 vector 中 if (points.empty()) { return 0; } sort(points.begin(), points.end(), [](const vector<int>& u, const vector<int>& v) ->bool{ return u[1] < v[1];//lambda表达式 }); int pos = points[0][1]; int ans = 1; for (const vector<int>& balloon: points) { if (balloon[0] > pos) { pos = balloon[1]; ++ans; } } return ans; }};
- 1
4. 根据身高和序号重组队列
406. 根据身高重建队列 中等
5. 买卖股票最大的收益
121. 买卖股票的最佳时机 简单
6. 买卖股票的最大收益 II
122. 买卖股票的最佳时机 II 简单
7. 种植花朵
605. 种花问题 简单
8. 判断是否为子序列
392. 判断子序列 简单
9. 修改一个数成为非递减数组
665. 非递减数列 简单
10. 子数组最大的和
53. 最大子序和 简单
11. 分隔字符串使同种字符出现在一起
763. 划分字母区间 简单
4、二分查找(6题)
正常实现
Input : [1,2,3,4,5]key : 3return the index : 2public int binarySearch(int[] nums, int key) { int l = 0, h = nums.length - 1; while (l <= h) { int m = l + (h - l) / 2; if (nums[m] == key) { return m; } else if (nums[m] > key) { h = m - 1; } else { l = m + 1; } } return -1;}
- 1
时间复杂度
二分查找也称为折半查找,每次都能将查找区间减半,这种折半特性的算法时间复杂度为 O(logN)。
m 计算
有两种计算中值 m 的方式:
- m = (l + h) / 2
- m = l + (h - l) / 2
l + h 可能出现加法溢出,也就是说加法的结果大于整型能够表示的范围。但是 l 和 h 都为正数,因此 h - l 不会出现加法溢出问题。所以,最好使用第二种计算法方法。
未成功查找的返回值
循环退出时如果仍然没有查找到 key,那么表示查找失败。可以有两种返回值:
- -1:以一个错误码表示没有查找到 key
- l:将 key 插入到 nums 中的正确位置
变种
二分查找可以有很多变种,实现变种要注意边界值的判断。例如在一个有重复元素的数组中查找 key 的最左位置的实现如下:
public int binarySearch(int[] nums, int key) { int l = 0, h = nums.length; while (l < h) { int m = l + (h - l) / 2; if (nums[m] >= key) { h = m; } else { l = m + 1; } } return l;}
- 1
该实现和正常实现有以下不同:
- h 的赋值表达式为 h = m
- 循环条件为 l < h
- 最后返回 l 而不是 -1
在 nums[m] >= key 的情况下,可以推导出最左 key 位于 [l, m] 区间中,这是一个闭区间。h 的赋值表达式为 h = m,因为 m 位置也可能是解。
在 h 的赋值表达式为 h = m 的情况下,如果循环条件为 l <= h,那么会出现循环无法退出的情况,因此循环条件只能是 l < h。以下演示了循环条件为 l <= h 时循环无法退出的情况:
nums = {0, 1, 2}, key = 1l m h0 1 2 nums[m] >= key0 0 1 nums[m] < key1 1 1 nums[m] >= key1 1 1 nums[m] >= key...
- 1
当循环体退出时,不表示没有查找到 key,因此最后返回的结果不应该为 -1。为了验证有没有查找到,需要在调用端判断一下返回位置上的值和 key 是否相等。
【完成】1. 求开方
求开方的思想就是不断的变更搜索范围,通过不断变更 L 和 R 这两个左右边界进行。
注意事项:这题千万要注意边界条件
69. x 的平方根 简单
【二分查找法】
向上取整公式:
L + ( R − L + 1 ) / 2 ( 其 中 的 R − L + 1 就 是 数 组 的 元 素 的 数 量 ) L+(R-L+1)/2 (其中的R-L+1就是数组的元素的数量) L+(R−L+1)/2(其中的R−L+1就是数组的元素的数量)
向下取整公式:
L + ( R − L ) / 2 L+(R-L)/2 L+(R−L)/2
//力扣官解class Solution {public: int mySqrt(int x) { int l = 0, r = x, ans = -1; while (l <= r) { int mid = l + (r - l) / 2; if ((long long)mid * mid <= x) { ans = mid; l = mid + 1; } else { r = mid - 1; } } return ans; }};
- 1
//简化版的二分查找法(自己写的)class Solution {public: int mySqrt(int x) { int l=0; int right = x / 2; if(x==0) return 0; if(x==1) return 1; while(l<r){ int mid=l+(r-l+1)/2; if(mid>x/mid){ r=mid-1; } else{ l=mid; } } return l; }};
- 1
//简化版的二分查找法(别人写的java版)public class Solution { public int mySqrt(int x) { // 特殊值判断 if (x == 0) { return 0; } if (x == 1) { return 1; } int left = 1; int right = x / 2; // 在区间 [left..right] 查找目标元素 while (left < right) { int mid = left + (right - left + 1) / 2; // 注意:这里为了避免乘法溢出,改用除法 if (mid > x / mid) { // 下一轮搜索区间是 [left..mid - 1] right = mid - 1; } else { // 下一轮搜索区间是 [mid..right] left = mid; } } return left; }}
- 1
【牛顿迭代法】
// fabs() 求绝对值//官解牛顿迭代class Solution {public: int mySqrt(int x) { if (x == 0) { return 0; } double C = x, x0 = x; //x0是选定的迭代初始值,C就是x(注意是double) while (true) { //一直执行到 break 为止 double xi = 0.5 * (x0 + C / x0); //新的迭代解 if (fabs(x0 - xi) < 1e-7) { //计算误差 break; } x0 = xi; //更新迭代解 } return int(x0); }};
- 1
//精简版牛顿迭代(这个不是很好理解)class Solution {public: int mySqrt(int x) { if (x == 0) return 0; double t=x; while (t*t-x>=1) t=0.5*(t+x/t);//这个判断条件为什么是 1, 没看懂 return int(t); }};
- 1
2. 大于给定元素的最小元素
744. 寻找比目标字母大的最小字母 简单
3. 有序数组的 Single Element
540. 有序数组中的单一元素 中等
4. 第一个错误的版本
278. 第一个错误的版本 简单
5. 旋转数组的最小数字
153. 寻找旋转排序数组中的最小值 中等
6. 查找区间
34. 在排序数组中查找元素的第一个和最后一个位置 中等
5、分治(2题)
【完成】1. 给表达式加括号
241. 为运算表达式设计优先级 中等
// substr的用法
- 用途:一种构造string的方法
- 形式:s.substr(pos, n)
- 解释:返回一个string,包含s中从pos开始的n个字符的拷贝(pos的默认值是0,n的默认值是s.size() - pos,即不加参数会默认拷贝整个s)
- 补充:若pos的值超过了string的大小,则substr函数会抛出一个out_of_range异常;若pos+n的值超过了string的大小,则substr会调整n的值,只拷贝到string的末尾
// push_back()函数的用法
函数将一个新的元素加到vector的最后面,位置为当前最后一个元素的下一个元素
官解(加了自己的注释)
class Solution {public: vector<int> diffWaysToCompute(string expression) { // 存储中间值 vector<int> count; for(int i = 0; i < expression.size(); i ++) {//这个for相当于遍历了所有的情况 char c = expression[i]; // 找到运算符 if(c == '+' || c == '-' || c == '*') { // 运算符左边的运算结果 vector<int> left = diffWaysToCompute(expression.substr(0, i));//从0开始的i个元素,刚好是0 ~ i-1 // 运算符右边的运算结果 vector<int> right = diffWaysToCompute(expression.substr(i + 1));//从n+1到string末尾 // 左右两边继续运算 for(int& l : left) { for(int& r : right) { switch(c) { case '+': count.push_back(l + r);//看起来 count 一直有数据 put_back 进去,其实都作为返回值 return 进入 l 或者 r 中了,所以外层的 count 中是没有值的 break; case '-': count.push_back(l - r); break; case '*': count.push_back(l * r); break; } } } } } // count为空说明当前无运算符,只是单独的数字,直接放入count中 if(count.size() == 0) { count.push_back(stoi(expression));//stoi()是C++的字符处理函数,把数字字符串转换成int输出 } return count; }};
- 1
别人的解法(用 if 代替switch,看起来简洁)
class Solution {public: vector<int> diffWaysToCompute(string input) { vector<int> vec1, vec2, res; int n = input.size(); int flag = 0; for(int i=0; i<n; i++){ if(input[i] == '+' || input[i] == '-' || input[i] == '*'){ flag = 1; // flag=1说明string是表达式,flag=0说明string是一个数字 vec1 = diffWaysToCompute(string(input, 0, i)); // 从第0个开始,存i个字符 vec2 = diffWaysToCompute(string(input, i+1, n-i-1)); for(int v1:vec1){ for(int v2:vec2){ if(input[i] == '+') res.push_back(v1+v2); if(input[i] == '-') res.push_back(v1-v2); if(input[i] == '*') res.push_back(v1*v2); } } } } if(flag==0) return {std::stoi(input)}; return res; }};
- 1
#include <vector>#include <iostream>#include <string>#include <cctype>class Solution {public: std::vector<int> diffWaysToCompute(std::string input) { int number = 0; if (tryIfNumber(input, &number)) { return {number}; } std::vector<int> result; for (auto i = 0; i < input.size(); ++i) { auto c = input[i]; if (isOperator(c)) { auto leftResult = diffWaysToCompute(input.substr(0, i)); auto rightResult = diffWaysToCompute(input.substr(i+1)); for (const auto &left : leftResult) { for (const auto &right : rightResult) { if (c == '+') { result.emplace_back(left + right); } else if (c == '-') { result.emplace_back(left - right); } else if (c == '*') { result.emplace_back(left * right); } } } } } return result; }private: bool tryIfNumber(const std::string &str, int *number) const { *number = 0; for (const auto &c : str) { if (std::isdigit(c)) { *number = *number * 10 + (c - '0'); } else { *number = 0; return false; } } return true; } bool isOperator(const char &c) const { return c == '+' || c == '-' || c == '*'; }};int main() { Solution sln; std::vector<std::string> inputs{"2-1-1", "2*3-4*5"}; auto print_v = [](const std::vector<int> &computes) { std::cout << "["; for (const auto &c : computes) { std::cout << c << ", "; } std::cout << "]" << std::endl; }; for (auto &input : inputs) { print_v(sln.diffWaysToCompute(input)); }}
- 1
2. 不同的二叉搜索树
95. 不同的二叉搜索树 II 中等
6、搜索(3+5+15=23题)
深度优先搜索和广度优先搜索广泛运用于树和图中,但是它们的应用远远不止如此。
BFS
广度优先搜索一层一层地进行遍历,每层遍历都是以上一层遍历的结果作为起点,遍历一个距离能访问到的所有节点。需要注意的是,遍历过的节点不能再次被遍历。
第一层:
- 0 -> {6,2,1,5}
第二层:
- 6 -> {4}
- 2 -> {}
- 1 -> {}
- 5 -> {3}
第三层:
- 4 -> {}
- 3 -> {}
每一层遍历的节点都与根节点距离相同。设 di 表示第 i 个节点与根节点的距离,推导出一个结论:对于先遍历的节点 i 与后遍历的节点 j,有 di <= dj。利用这个结论,可以求解最短路径等 最优解 问题:第一次遍历到目的节点,其所经过的路径为最短路径。应该注意的是,使用 BFS 只能求解无权图的最短路径,无权图是指从一个节点到另一个节点的代价都记为 1。
在程序实现 BFS 时需要考虑以下问题:
- 队列:用来存储每一轮遍历得到的节点;
- 标记:对于遍历过的节点,应该将它标记,防止重复遍历。
1. 计算在网格中从原点到特定点的最短路径长度
2. 组成整数的最小平方数数量
3. 最短单词路径
DFS
广度优先搜索一层一层遍历,每一层得到的所有新节点,要用队列存储起来以备下一层遍历的时候再遍历。
而深度优先搜索在得到一个新节点时立即对新节点进行遍历:从节点 0 出发开始遍历,得到到新节点 6 时,立马对新节点 6 进行遍历,得到新节点 4;如此反复以这种方式遍历新节点,直到没有新节点了,此时返回。返回到根节点 0 的情况是,继续对根节点 0 进行遍历,得到新节点 2,然后继续以上步骤。
从一个节点出发,使用 DFS 对一个图进行遍历时,能够遍历到的节点都是从初始节点可达的,DFS 常用来求解这种 可达性 问题。
在程序实现 DFS 时需要考虑以下问题:
- 栈:用栈来保存当前节点信息,当遍历新节点返回时能够继续遍历当前节点。可以使用递归栈。
- 标记:和 BFS 一样同样需要对已经遍历过的节点进行标记。
1. 查找最大的连通面积
695. 岛屿的最大面积 中等
2. 矩阵中的连通分量数目
200. 岛屿数量 中等
3. 好友关系的连通分量数目
4. 填充封闭区域
5. 能到达的太平洋和大西洋的区域
Backtracking
Backtracking(回溯)属于 DFS。
- 普通 DFS 主要用在 可达性问题 ,这种问题只需要执行到特点的位置然后返回即可。
- 而 Backtracking 主要用于求解 排列组合 问题,例如有 { ‘a’,‘b’,‘c’ } 三个字符,求解所有由这三个字符排列得到的字符串,这种问题在执行到特定的位置返回之后还会继续执行求解过程。
因为 Backtracking 不是立即返回,而要继续求解,因此在程序实现时,需要注意对元素的标记问题:
- 在访问一个新元素进入新的递归调用时,需要将新元素标记为已经访问,这样才能在继续递归调用时不用重复访问该元素;
- 但是在递归返回时,需要将元素标记为未访问,因为只需要保证在一个递归链中不同时访问一个元素,可以访问已经访问过但是不在当前递归链中的元素。
1. 数字键盘组合
2. IP 地址划分
3. 在矩阵中寻找字符串
79. 单词搜索
4. 输出二叉树中所有从根到叶子的路径
5. 排列
46. 全排列
6. 含有相同元素求排列
7. 组合
77. 组合
8. 组合求和
39. 组合总和
9. 含有相同元素的组合求和
10. 1-9 数字的组合求和
11. 子集
78. 子集
12. 含有相同元素求子集
13. 分割字符串使得每个部分都是回文数
14. 数独
37. 解数独
15. N 皇后
51. N 皇后
7、动态规划(5+2+2+3+3+1+7+4+3=30题)
递归和动态规划都是将原问题拆成多个子问题然后求解,他们之间最本质的区别是,动态规划保存了子问题的解,避免重复计算。
斐波那契数列
1. 爬楼梯
70. 爬楼梯 简单
动态规划(滚动数组)
class Solution {public: int climbStairs(int n) { int p=0; int q=1; int r=p+q; for(int i=2;i<=n;i++){ p=q; q=r; r=p+q; } return r; }};
- 1
带记忆的递归
- 1
斐波那契数列通项公式法
class Solution {public: int climbStairs(int n) { double sqrt5 = sqrt(5); double fibn = pow((1 + sqrt5) / 2, n + 1) - pow((1 - sqrt5) / 2, n + 1); return (int)round(fibn / sqrt5); }};
- 1
2. 强盗抢劫
198. 打家劫舍 中等
3. 强盗在环形街区抢劫
213. 打家劫舍 II 中等
4. 信件错排
5. 母牛生产
[程序员代码面试指南-P181](https://github.com/CyC2018/CS-Notes/blob/master/notes/Leetcode 题解 - 动态规划.md#)
矩阵路径
1. 矩阵的最小路径和
64. 最小路径和 中等
2. 矩阵的总路径数
62. 不同路径 中等
数组区间
1. 数组区间和
303. 区域和检索 - 数组不可变 简单
2. 数组中等差递增子区间的个数
413. 等差数列划分 中等
分割整数
1. 分割整数的最大乘积
343. 整数拆分 中等
2. 按平方数来分割整数
279. 完全平方数 中等
3. 分割整数构成字母字符串
91. 解码方法 中等
最长递增子序列
已知一个序列 {S1, S2,…,Sn},取出若干数组成新的序列 {Si1, Si2,…, Sim},其中 i1、i2 … im 保持递增,即新序列中各个数仍然保持原数列中的先后顺序,称新序列为原序列的一个 子序列 。
如果在子序列中,当下标 ix > iy 时,Six > Siy,称子序列为原序列的一个 递增子序列 。
定义一个数组 dp 存储最长递增子序列的长度,dp[n] 表示以 Sn 结尾的序列的最长递增子序列长度。对于一个递增子序列 {Si1, Si2,…,Sim},如果 im < n 并且 Sim < Sn,此时 {Si1, Si2,…, Sim, Sn} 为一个递增子序列,递增子序列的长度增加 1。满足上述条件的递增子序列中,长度最长的那个递增子序列就是要找的,在长度最长的递增子序列上加上 Sn 就构成了以 Sn 为结尾的最长递增子序列。因此 dp[n] = max{ dp[i]+1 | Si < Sn && i < n} 。
因为在求 dp[n] 时可能无法找到一个满足条件的递增子序列,此时 {Sn} 就构成了递增子序列,需要对前面的求解方程做修改,令 dp[n] 最小为 1,即:
对于一个长度为 N 的序列,最长递增子序列并不一定会以 SN 为结尾,因此 dp[N] 不是序列的最长递增子序列的长度,需要遍历 dp 数组找出最大值才是所要的结果,max{ dp[i] | 1 <= i <= N} 即为所求。
1. 最长递增子序列
300. 最长递增子序列 中等
2. 一组整数对能够构成的最长链
646. 最长数对链 中等
3. 最长摆动子序列
376. 摆动序列 中等
最长公共子序列
对于两个子序列 S1 和 S2,找出它们最长的公共子序列。
定义一个二维数组 dp 用来存储最长公共子序列的长度,其中 dp[i][j] 表示 S1 的前 i 个字符与 S2 的前 j 个字符最长公共子序列的长度。考虑 S1i 与 S2j 值是否相等,分为两种情况:
- 当 S1i==S2j 时,那么就能在 S1 的前 i-1 个字符与 S2 的前 j-1 个字符最长公共子序列的基础上再加上 S1i 这个值,最长公共子序列长度加 1,即 dp[i][j] = dp[i-1][j-1] + 1。
- 当 S1i != S2j 时,此时最长公共子序列为 S1 的前 i-1 个字符和 S2 的前 j 个字符最长公共子序列,或者 S1 的前 i 个字符和 S2 的前 j-1 个字符最长公共子序列,取它们的最大者,即 dp[i][j] = max{ dp[i-1][j], dp[i][j-1] }。
综上,最长公共子序列的状态转移方程为:
对于长度为 N 的序列 S1 和长度为 M 的序列 S2,dp[N][M] 就是序列 S1 和序列 S2 的最长公共子序列长度。
与最长递增子序列相比,最长公共子序列有以下不同点:
- 针对的是两个序列,求它们的最长公共子序列。
- 在最长递增子序列中,dp[i] 表示以 Si 为结尾的最长递增子序列长度,子序列必须包含 Si ;在最长公共子序列中,dp[i][j] 表示 S1 中前 i 个字符与 S2 中前 j 个字符的最长公共子序列长度,不一定包含 S1i 和 S2j。
- 在求最终解时,最长公共子序列中 dp[N][M] 就是最终解,而最长递增子序列中 dp[N] 不是最终解,因为以 SN 为结尾的最长递增子序列不一定是整个序列最长递增子序列,需要遍历一遍 dp 数组找到最大者。
1. 最长公共子序列
1143. 最长公共子序列 中等
0-1 背包
有一个容量为 N 的背包,要用这个背包装下物品的价值最大,这些物品有两个属性:体积 w 和价值 v。
定义一个二维数组 dp 存储最大价值,其中 dp[i][j] 表示前 i 件物品体积不超过 j 的情况下能达到的最大价值。设第 i 件物品体积为 w,价值为 v,根据第 i 件物品是否添加到背包中,可以分两种情况讨论:
- 第 i 件物品没添加到背包,总体积不超过 j 的前 i 件物品的最大价值就是总体积不超过 j 的前 i-1 件物品的最大价值,dp[i][j] = dp[i-1][j]。
- 第 i 件物品添加到背包中,dp[i][j] = dp[i-1][j-w] + v。
第 i 件物品可添加也可以不添加,取决于哪种情况下最大价值更大。因此,0-1 背包的状态转移方程为:
// W 为背包总体积// N 为物品数量// weights 数组存储 N 个物品的重量// values 数组存储 N 个物品的价值public int knapsack(int W, int N, int[] weights, int[] values) { int[][] dp = new int[N + 1][W + 1]; for (int i = 1; i <= N; i++) { int w = weights[i - 1], v = values[i - 1]; for (int j = 1; j <= W; j++) { if (j >= w) { dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - w] + v); } else { dp[i][j] = dp[i - 1][j]; } } } return dp[N][W];}
- 1
空间优化
在程序实现时可以对 0-1 背包做优化。观察状态转移方程可以知道,前 i 件物品的状态仅与前 i-1 件物品的状态有关,因此可以将 dp 定义为一维数组,其中 dp[j] 既可以表示 dp[i-1][j] 也可以表示 dp[i][j]。此时,
因为 dp[j-w] 表示 dp[i-1][j-w],因此不能先求 dp[i][j-w],防止将 dp[i-1][j-w] 覆盖。也就是说要先计算 dp[i][j] 再计算 dp[i][j-w],在程序实现时需要按倒序来循环求解。
public int knapsack(int W, int N, int[] weights, int[] values) { int[] dp = new int[W + 1]; for (int i = 1; i <= N; i++) { int w = weights[i - 1], v = values[i - 1]; for (int j = W; j >= 1; j--) { if (j >= w) { dp[j] = Math.max(dp[j], dp[j - w] + v); } } } return dp[W];}
- 1
无法使用贪心算法的解释
0-1 背包问题无法使用贪心算法来求解,也就是说不能按照先添加性价比最高的物品来达到最优,这是因为这种方式可能造成背包空间的浪费,从而无法达到最优。考虑下面的物品和一个容量为 5 的背包,如果先添加物品 0 再添加物品 1,那么只能存放的价值为 16,浪费了大小为 2 的空间。最优的方式是存放物品 1 和物品 2,价值为 22.
| id | w | v | v/w |
|---|---|---|---|
| 0 | 1 | 6 | 6 |
| 1 | 2 | 10 | 5 |
| 2 | 3 | 12 | 4 |
变种
- 完全背包:物品数量为无限个
- 多重背包:物品数量有限制
- 多维费用背包:物品不仅有重量,还有体积,同时考虑这两种限制
- 其它:物品之间相互约束或者依赖
1. 划分数组为和相等的两部分
416. 分割等和子集 中等
2. 改变一组数的正负号使得它们的和为一给定数
494. 目标和 中等
3. 01 字符构成最多的字符串
474. 一和零 中等
4. 找零钱的最少硬币数
322. 零钱兑换 中等
5. 找零钱的硬币数组合
518. 零钱兑换 II 中等
6. 字符串按单词列表分割
139. 单词拆分 中等
7. 组合总和
377. 组合总和 Ⅳ 中等
股票交易
1. 需要冷却期的股票交易
309. 最佳买卖股票时机含冷冻期 中等
2. 需要交易费用的股票交易
714. 买卖股票的最佳时机含手续费 中等
3. 只能进行两次的股票交易
123. 买卖股票的最佳时机 III 困难
4. 只能进行 k 次的股票交易
188. 买卖股票的最佳时机 IV 困难
字符串编辑
1. 删除两个字符串的字符使它们相等
583. 两个字符串的删除操作 中等
2. 编辑距离
72. 编辑距离 困难
3. 复制粘贴字符
650. 只有两个键的键盘 中等
8、数学(3+3+1+2+1+1+4=15题)
【无】素数分解
每一个数都可以分解成素数的乘积,例如 84 = 22 * 31 * 50 * 71 * 110 * 130 * 170 * …
【无】整除
令 x = 2m0 * 3m1 * 5m2 * 7m3 * 11m4 * …
令 y = 2n0 * 3n1 * 5n2 * 7n3 * 11n4 * …
如果 x 整除 y(y mod x == 0),则对于所有 i,mi <= ni。
最大公约数最小公倍数
x 和 y 的最大公约数为:gcd(x,y) = 2min(m0,n0) * 3min(m1,n1) * 5min(m2,n2) * …
x 和 y 的最小公倍数为:lcm(x,y) = 2max(m0,n0) * 3max(m1,n1) * 5max(m2,n2) * …
【完成】1. 生成素数序列
204. 计数质数 简单
暴力法:
class Solution {public: int countPrimes(int n) { if(n<2) return 0; int count=0; int j=0; for(int i=2;i<n;i++){ count++;//这步是精髓 for(j=2;j<=sqrt(i);j++){ if(i%j==0){ count--;//这步是精髓 break; } } } return count; }};
- 1
埃及筛
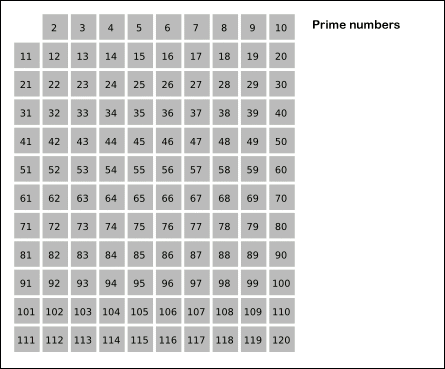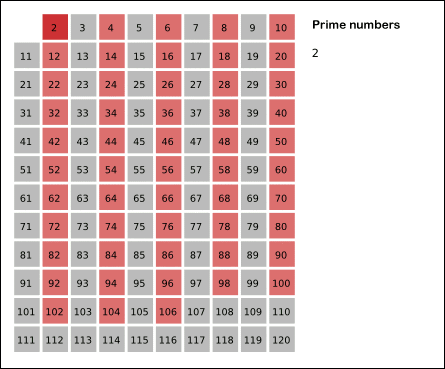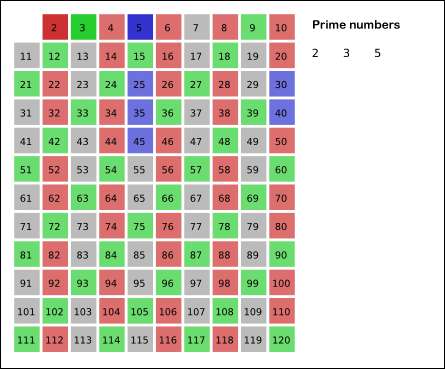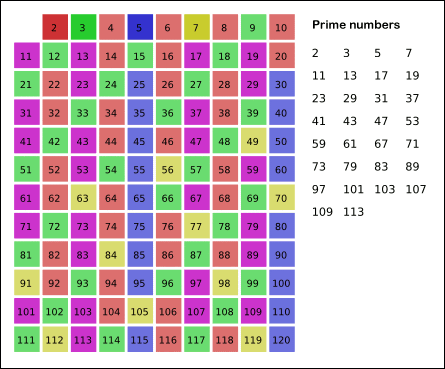
注意:
这种没有改进的埃及筛做了很多无用功
每次都从头开始标记会导致很多已经被标记过的元素重新被标记一遍,比如 3个 i,在前面一定在标记质数 3 的时候,作为 3 的倍数被标记过 i 个 3
//没有改进的埃及筛(会超时)class Solution {public: int countPrimes(int n) { vector<int> isPrime(n,1);//可以适当设置大一点,因为最后检查是否质数的时候会跳过n int ans=0; for(int i=2;i<n;i++){ if(isPrime[i]){ ans++; //if ((long long)i * i < n) { for (int j = 2; j < n; j ++) {//每一次都会从头开始标记,但其实前面的是已经标记过的 if(j%i==0){ isPrime[j] = 0; } } // } } } return ans; }};
- 1
改进后的埃及筛
class Solution {public: int countPrimes(int n) { vector<int> isPrime(n,1);//可以适当设置大一点,因为最后检查是否质数的时候会跳过n int ans=0; for(int i=2;i<n;i++){ if(isPrime[i]){ ans++; if ((long long)i * i < n) {//因为我们所需要标记的范围就是 i*i ,如果 i*i >= n就不需要标记了,说明已经全部标记完了 for (int j = i * i; j < n; j += i) { isPrime[j] = 0; } } } } return ans; }};
- 1
线性筛(不在面试范畴)
【无】2. 最大公约数
【无】3. 使用位操作和减法求解最大公约数
[编程之美:2.7](https://github.com/CyC2018/CS-Notes/blob/master/notes/Leetcode 题解 - 数学.md#)
进制转换
【完成】1. 7 进制
504. 七进制数 简单
取模运算
思路:
- 记录负号,负数取正
- 逐位提取,先模后除
- 0要特判,否则WA
- 负号补上,答案翻转
class Solution {public: string convertToBase7(int num) { if(num==0) return "0";//边缘情况 string ans; ans.reserve(9); string sign= num<0 ? "-":""; if(num<0) num=abs(num); while(num){//进制转化 ans+= '0' + (num % 7);//注意这个单引号 num /= 7; } ans+=sign;//加上符号 reverse(ans.begin(),ans.end()); return ans; }};
- 1
递归
只能用于10以内的进制运算
否则没法用数字表示,就不能使用这种方法
#include<sstream>class Solution {public: int convert(int num){ if(num < 7 && num > -7) return num; //如果就一位数 return convert(num / 7)*10 + num % 7; } string convertToBase7(int num) { int b = convert(num); //进入递归函数,返回进制转换后的 int 数 string c; //将 int 数转换为 string 返回 c.reserve(9); c=to_string(b); return c; }};
- 1
【完成】2. 16 进制
405. 数字转换为十六进制数 简单
移位解法
class Solution {public: string toHex(int num) { if (num == 0){//特殊情况处理 return "0"; } // 0-15映射成字符 string num2char = "0123456789abcdef";//这样就可以用 int 下标运算符去读取正确的表达了 // 转为为非符号数 unsigned int n = num;//因为C++负数不支持移位运算符 string res = ""; //res为空 while (n > 0){ //这种方式就是二进制转16进制的典型方法,取四位算它的值 res = num2char[n&15] + res; //n&15用于去除除了最后四位二进制数前面的数,15=000...0001111 n >>= 4;//删除最后的四位 } return res; }};
- 1
~【完成】3. 26 进制(这题直接背)
168. Excel表列名称 简单
思路
以数字 486 为例示范 10 进制与其他进制的转换过程:
通过**【除留余数法】**将数字 486 由 10 进制转换为 10 进制

10 的 3 次幂大于 486 循环结束
可拆解出 10 进制数的个位、十位、百位…,再反向罗列得到 486
同理,通过【除留余数法】将数字 486 由 10 进制转换为 2 进制

2 的 9 次幂大于 486 循环结束
可拆解出 2 进制数 逻辑上的 个位、十位、百位…,再反向罗列得到 111100110
两种不同思路的代码
class Solution {public: string convertToTitle(int columnNumber) { string res=""; while (columnNumber > 0) { int remainer = columnNumber % 26; if(remainer == 0){ remainer = 26; columnNumber -= 1; } res.push_back('A' + remainer - 1); columnNumber /= 26; } reverse(res.begin(),res.end()); return res; }};
- 1
//class Solution {public: string convertToTitle(int columnNumber) { string s=""; while(columnNumber>0){ columnNumber-=1; s+='A'+columnNumber%26; columnNumber/=26; } reverse(s.begin(),s.end()); return s; }};
- 1
阶乘
【完成】1. 统计阶乘尾部有多少个 0
172. 阶乘后的零 简单
【寻找5元素】
class Solution {public: int trailingZeroes(int n) { int count=0; for(int i=1;i<=n;i++){ int N=i;//小心这里,会改变i的值 while(N%5==0) { count++; N/=5; } } return count; }};
- 1
【寻找元素5】更简洁的
class Solution {public: int trailingZeroes(int n) { int count = 0; while (n > 0) { count += n / 5; n = n / 5; } return count; }};
- 1
字符串加法减法
【完成】1. 二进制加法
67. 二进制求和 简单
思路:
1、补 0 的思想很重要
class Solution {public: string addBinary(string a, string b) { reverse(a.begin(),a.end()); reverse(b.begin(),b.end()); string sum=""; int carry=0; int min=a.length()<b.length()? a.length():b.length(); int max=a.length()>b.length()? a.length():b.length(); for(int j=min;j<max;j++){//补齐缺少的0 if(a.length()<b.length()){//a短 a+='0'; } else{ b+='0'; } } for(int i=0;i<a.length()&&i<b.length();i++){//二进制运算 sum.push_back(a[i]-48+b[i]+carry); carry=0;//这是上一个进位 if(sum[i]=='2'||sum[i]=='3') { carry=1; sum[i]-=2; } } if(carry==1) sum.push_back('1');//处理最后的进位 reverse(sum.begin(),sum.end()); return sum; }};
- 1
【完成】2. 字符串加法
415. 字符串相加 简单
在上面的基础上改动一点点即可
class Solution {public: string addStrings(string a, string b) { reverse(a.begin(),a.end()); reverse(b.begin(),b.end()); string sum=""; int carry=0; int min=a.length()<b.length()? a.length():b.length(); int max=a.length()>b.length()? a.length():b.length(); for(int j=min;j<max;j++){//补齐缺少的0 if(a.length()<b.length()){//a短 a+='0'; } else{ b+='0'; } } for(int i=0;i<a.length()&&i<b.length();i++){//二进制运算 sum.push_back(a[i]-'0'+b[i]+carry); carry=0;//这是上一个进位 if(sum[i]>'9') { carry=1; sum[i]-=10; } } if(carry==1) sum.push_back('1');//处理最后的进位 reverse(sum.begin(),sum.end()); return sum; }};
- 1
相遇问题
1. 改变数组元素使所有的数组元素都相等
多数投票问题
【完成】1. 数组中出现次数多于 n / 2 的元素
169. 多数元素 简单
排序法
class Solution { public: int majorityElement(vector<int>& nums){ sort(nums.begin(),nums.end()); return nums[nums.size()/2]; }};
- 1
哈希表法
会超时
其它
【完成】1. 平方数
367. 有效的完全平方数 简单
暴力法(会超时)
class Solution {public://暴力法 bool isPerfectSquare(int num) { if(num==0||num==1) return true; for(int i=1;i<=num/2;i++){ if(i==num/i && num%i==0) return true; } return false; }};
- 1
二分查找法
class Solution {public://二分查找法 bool isPerfectSquare(int num) { if(num==0||num==1||num==4) return true;//特殊情况判定 int low=1; int high=num/2; int mid=(low+high)/2; while(low<high){ mid=(low+high)/2; if(low==mid) return false;//此时low==high-1,接着会陷入死循环,这时候的开方答案应该是介于low和high之间的那个小数 if(mid==num/mid && num%mid==0) return true; else if((long long)mid*mid>num){ high=mid; } else low=mid; } return false; }};
- 1
==数学法:==首项为1 公差为2的等差数列之和刚好为完全平方数,因此可以根据这个原理来解题
class Solution {public://二分查找法 bool isPerfectSquare(int num) { int tmp = 1; while(num > 0) { num -= tmp; tmp += 2; } return num == 0; }};
- 1
遇到求根题可以直接想到牛顿迭代法
牛顿迭代法
第一种官解:
class Solution {public: bool isPerfectSquare(int num) { if(num<2) return true; long x0=num/2; while (x0 * x0 > num) { x0 = (x0 + num / x0) / 2; } return (x0 * x0 == num); } };
- 1
第二种:double版牛顿迭代法
class Solution {public: bool isPerfectSquare(int num) { if(num<2) return true; double x0=num/2; while(true){ double x1=0.5*(x0+num/x0); if(fabs(x1-x0)<1e-7) break; x0=x1; } return (long long)x0 * (long long)x0==num; } };
- 1
【完成】2. 3 的 n 次方
326. 3的幂 简单
暴力法
class Solution {public://暴力解法:遍历 bool isPowerOfThree(int n) { if(n==0) return false; while(n%3==0){ n/=3; } if(n==1) return true; return false; }};
- 1
【完成】3. 乘积数组
238. 除自身以外数组的乘积 中等
暴力解法:会超时
class Solution {public: vector<int> productExceptSelf(vector<int>& nums) { vector<int> output(nums.size(),0); for(int i=0;i<nums.size();i++){ int left=0; int right=i+1; int product=1; for(;left<i;left++){ product*=nums[left]; } for(;right<nums.size();right++){ product*=nums[right]; } output[i]=product; } return output; }};
- 1
左右乘积列表

class Solution {public: vector<int> productExceptSelf(vector<int>& nums) { vector<int> L(nums.size(),1);//在初始化是就将L[0]的前缀之积设置为1,后面循环时即可跳过L[0],R[0]同理 for(int i=1;i<nums.size();i++){ L[i]=L[i-1]*nums[i-1];//L[i-1]也就是nums[i-1]的前缀之积 } vector<int> R(nums.size(),1); for(int j=nums.size()-2;j>=0;j--){ R[j]=R[j+1]*nums[j+1]; } for(int i=0;i<nums.size();i++){ nums[i]=L[i]*R[i]; } return nums; }};
- 1
【完成】4. 找出数组中的乘积最大的三个数
628. 三个数的最大乘积 简单
排序法:
class Solution {public://基于快速排序的算法 int Partition(vector<int>& nums,int low,int high){ int pivot=nums[low]; while(low<high){ while(low<high&&nums[high]>=pivot) high--; nums[low]=nums[high]; while(low<high&&nums[low]<pivot) low++; nums[high]=nums[low]; } nums[low]=pivot; return low; } void QuickSort(vector<int>& nums,int low,int high){ if(low<high){ int pivot=Partition(nums,low,high); QuickSort(nums, low, pivot); QuickSort(nums, pivot+1, high); } } int maximumProduct(vector<int>& nums) { int product=1; QuickSort(nums,0,nums.size()-1); //sort(nums.begin(),nums.end()); int max1=nums[nums.size()-1] * nums[nums.size()-2] * nums[nums.size()-3]; int max2=nums[0] * nums[1] * nums[nums.size()-1]; return max1>max2?max1:max2; }};
- 1
方法二:线性扫描
在方法一中,我们实际上只要求出数组中最大的三个数以及最小的两个数,因此我们可以不用排序,用线性扫描直接得出这五个数。
四、数据结构相关
其实链表定义的时候,就是定义一个节点,链表就是很多节点连接起来,所以一个节点也叫链表
1、链表(10题)
链表刷题总结:
1、反转链表的基本方式:
设置 prev 和 curr 两个指针
prev=nullptr;//因为是反转链表,那么原头结点前的元素便是尾结点 nullptrnext=curr->next;//记录 curr->next,因为下一步会断掉原有的 curr->next 这个链接curr->next=prev;//断掉原有的链接,反转指向前一个数//下面两步将这 prev 和 curr 两个指针右移prev=curr;curr=next;
- 1
【完成】1. 找出两个链表的交点
160. 相交链表 简单
==【较聪明的双指针解法】==第一种解法:【双指针法】把两个链表连起来,也就是一个相同长度的链表了
*注意其中对 ListNode A = headA 的理解
class Solution {public: ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) { ListNode *A = headA, *B = headB;/*指向指针的指针,这里对比的是指针headA和指针HeadB是否相等(这个描述是错误的) ListNode *A = headA的正确理解:ListNode *A指的是定义一个指向 ListNode 类型的指针,A的值就等于headA中的值,也就是等于 headA 指向的节点的地址 之所以一开始理解不了是因为搞混了 int *a = b; 和 int *a = &b的区别, 第一种写法的意思就是指 a 是一个指向int类型的指针,a 等于 b 中存储的地址的值,b 本身也是一个指针。 第二种写法的意思是 a 指向 b 所以此处的 A 在后续改变值之前和 headA 完全等同,之所以要重新定义一个 A 是为了保存 headA 中的地址,不然后面需要用时就没有了 */ while (A != B) { A = (A != nullptr ? A->next : headB);//判断是否到达链表的尾部,如果到达尾部之后就继续遍历另一个链表,加了括号就好理解了 B = B != nullptr ? B->next : headA; } return A; }};
- 1
==【较笨的双指针解法】==第二种解法(以后可以写,此处未写):
思路:
1、首先分别遍历两个链表,得到每个链表的长度a,b
2、相差的长度让指向长链的指针先走b-a步
3、然后指向两个链表的两个指针同时运动,当两个指针指向的地址相同时就是两个链表相遇的地方
【哈希表法】
//哈希表法class Solution {public: ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) { //存入哈希表 ListNode *ptrA=headA, *ptrB=headB; unordered_map<ListNode*,int> T; while(ptrA!=NULL){ T[ptrA]=ptrA->val; ptrA = ptrA->next; } //搜索哈希表中是否有与ptrA相同的地址 while(ptrB!=NULL){ if(T.count(ptrB)){ return ptrB; } ptrB=ptrB->next; } return {}; }};
- 1
【完成】2. 链表反转
206. 反转链表 简单
【双指针法】
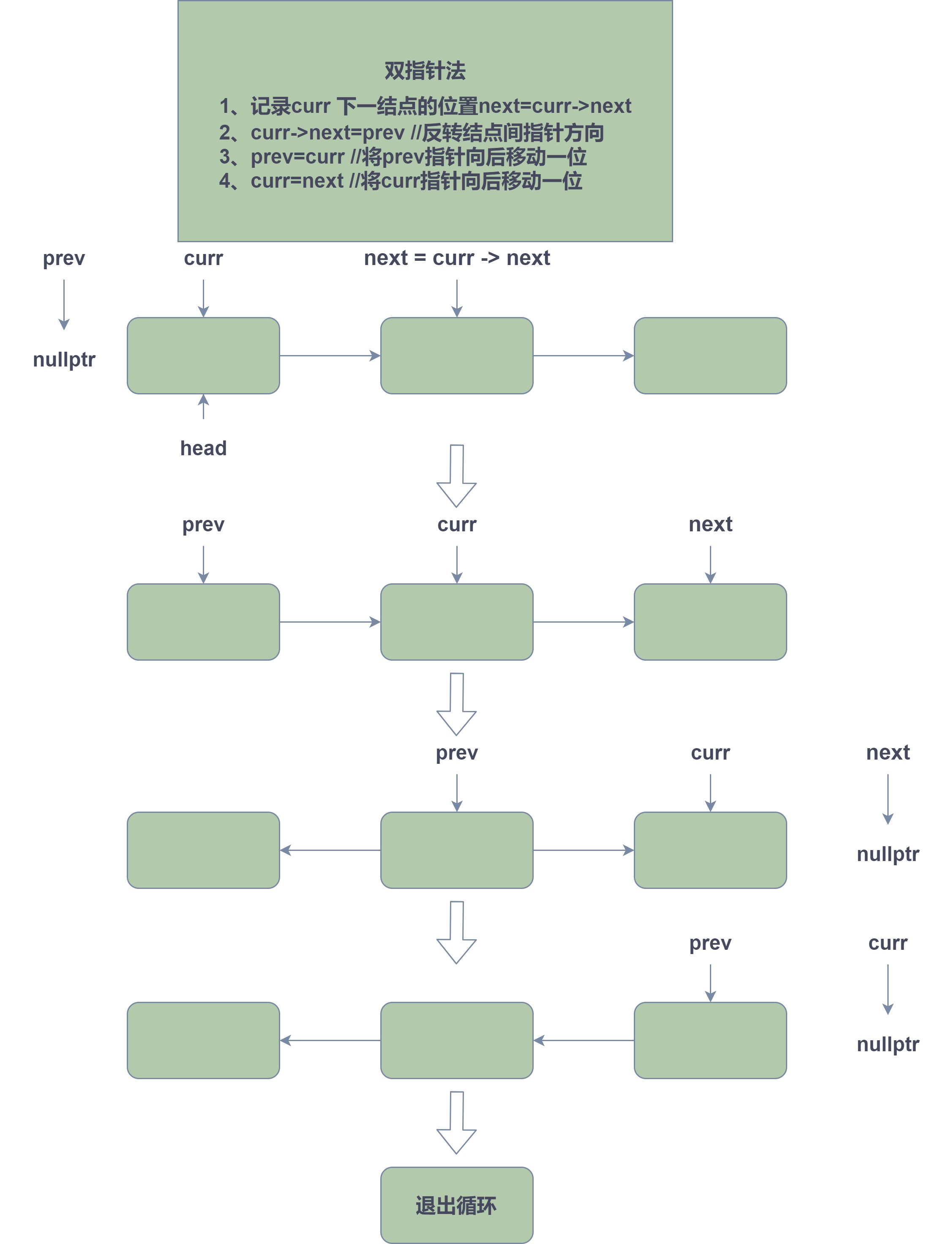
class Solution {public: ListNode* reverseList(ListNode* head) { ListNode* curr=head; ListNode* prev=nullptr; while(curr){ ListNode* next=curr->next; curr->next=prev;//这步断了后面的链接,往前面连接 prev=curr; curr=next; } return prev; }};
- 1
【递归法】还没看懂
class Solution {public: ListNode* reverseList(ListNode* head) { if (!head || !head->next) { return head; } ListNode* newHead = reverseList(head->next); head->next->next = head; head->next = nullptr; return newHead; }};
- 1
~【完成】3. 归并两个有序的链表
21. 合并两个有序链表 简单
【迭代法】
/** * Definition for singly-linked list. * struct ListNode { * int val; * ListNode *next; * ListNode() : val(0), next(nullptr) {} * ListNode(int x) : val(x), next(nullptr) {}//构造函数 * ListNode(int x, ListNode *next) : val(x), next(next) {} * }; */ //一开始想的解决方案都是在原来的链表中去插入,比较繁琐,简单的做法应该是:创建一个新链表,用一个指针控制这个链表的增长,另外另个待合并的链表只需要将需要的节点连接到新链表中,他们原来的顺序及指向不重要class Solution {public: ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) { ListNode* ans = new ListNode(-1);//记住这种创建链表的方法 ListNode* prev = ans;//将prev指向第一个节点 while(l1!=nullptr&&l2!=nullptr){//将两个链表合并 if(l1->val<l2->val){ prev->next=l1; l1=l1->next; } else{ prev->next=l2; l2=l2->next; } prev=prev->next; } //这里注意看一下为什么最后只剩下一个没有连接上去的节点 prev->next = l1 == nullptr ? l2 : l1; return ans->next; }};
- 1
【递归法】
还没看
【完成】4. 从有序链表中删除重复节点
哈希表法
/** * Definition for singly-linked list. * struct ListNode { * int val; * ListNode *next; * ListNode() : val(0), next(nullptr) {} * ListNode(int x) : val(x), next(nullptr) {} * ListNode(int x, ListNode *next) : val(x), next(next) {} * }; */ //哈希表法class Solution {public: ListNode* deleteDuplicates(ListNode* head) { if(head==nullptr) return head; unordered_set<int> table;//哈希表 table.insert(head->val);//将第一个元素存入哈希表 ListNode* temp=head->next;//temp指向 head->next ListNode* prev=head;//prev指向temp的前一个 while(temp!=nullptr){//将元素存入哈希表 if(table.count(temp->val)){//如果该元素存在 prev->next=temp->next;//跳过temp的当前节点 } else prev=prev->next; table.insert(temp->val); temp=temp->next; } return head; }};
- 1
还有一种**一次遍历法**,因为重复项是相邻的,因此可以使用这种方法,比较蠢
~【完成】5. 删除链表的倒数第 n 个节点
【哈希表法】
//哈希表法,记录下第n个数的地址,key值为n,val为地址class Solution {public: ListNode* removeNthFromEnd(ListNode* head, int n) { unordered_map<int,ListNode*> table;//注意此处的 ListNode* ListNode* temp=head; int i=0; while(temp!=nullptr){ table[i++]=temp;//存储第i个数字的地址, i-1 就是最终的节点个数 temp=temp->next; }//这个循环过后,其实i被多加了一次,所以这个链表的下标最大其实只有i-1,也就是有i个结点 if(i==n) return head->next;//防止倒数n+1这个结点不存在的情况 temp=table[i-n+-1]; //找到倒数第n+1个结点 temp->next=temp->next->next; return head; }};
- 1
快慢指针法
栈
双指针法

~【完成】6. 交换链表中的相邻结点
24. 两两交换链表中的节点 中等
三指针法
class Solution {public: ListNode* swapPairs(ListNode* head) { ListNode* dummy=new ListNode(0);//创建头结点 dummy->next=head; ListNode* temp=dummy; ListNode* l=head; if(head==nullptr) return head; ListNode* r=head->next; while(l->next!=nullptr){ temp->next=r; l->next=r->next; r->next=l; temp=l; if(l->next==nullptr) break; r=l->next->next; l=l->next; } return dummy->next; }};
- 1
递归
【完成】7. 链表求和
445. 两数相加 II 中等
官解栈
//官解class Solution {public: ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) { stack<int> s1, s2;//定义两个栈 while (l1) { s1.push(l1 -> val);//将l1压入栈中 l1 = l1 -> next; } while (l2) { s2.push(l2 -> val);//将l2压入栈中 l2 = l2 -> next; } int carry = 0; //设置进位 ListNode* ans = nullptr;//设置答案链表 while (!s1.empty() or !s2.empty() or carry != 0) { int a = s1.empty() ? 0 : s1.top();//判断是否为空,并记录下栈顶的元素 int b = s2.empty() ? 0 : s2.top(); if (!s1.empty()) s1.pop(); //将栈顶元素弹出 if (!s2.empty()) s2.pop(); int cur = a + b + carry; //计算当前位的值 carry = cur / 10; //进位 cur %= 10; //余数就是cur auto curnode = new ListNode(cur); //创建新结点 curnode -> next = ans; //从尾部开始创建链表,注意这种写法 ans = curnode; } return ans; }};
- 1
自己写的栈
思路:
1、将两个待加链表入栈
2、提取栈顶待加元素并将他们出栈
3、计算当前位的进位及余数
4、创建新的 ans 链表并返回,注意这里的创建链表思路
ListNode* ans=nullptr; //从末尾开始创建链表,因为新链表中还没有元素,因此将头结点先指向 nullptr ListNode* newNode=new ListNode(a); //创建 val=a 的新结点//下面两步是精华newNode->next=ans;ans=newNode;
- 1
//自己写的class Solution {public: ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) { stack<int> s1,s2; while(l1!=nullptr){ s1.push(l1->val); l1=l1->next; } while(l2!=nullptr){ s2.push(l2->val); l2=l2->next; } int curr=0; int carry=0; ListNode* ans=nullptr; while(!s1.empty()|!s2.empty()|carry!=0){ int a=s1.empty()?0:s1.top(); int b=s2.empty()?0:s2.top(); if(!s1.empty()) s1.pop(); if(!s2.empty()) s2.pop(); curr=a+b+carry; carry=curr/10; //curr=(a+b+carry)%10;//注意这里的carry被改变了,所以会错 curr=curr%10; ListNode* currnode=new ListNode(curr); currnode->next=ans; ans=currnode; } return ans; }};
- 1
【完成】8. 回文链表(这题精妙,多练)
234. 回文链表 简单
栈
class Solution { //栈public: bool isPalindrome(ListNode* head) { ListNode* temp=head; stack<int> s; while(temp!=nullptr){//入栈 s.push(temp->val); temp=temp->next; } temp=head; while(temp!=nullptr){ int a=s.empty()?0:s.top();//a=栈顶元素 if(!s.empty()) s.pop();//出栈 if(temp->val!=a) return false; temp=temp->next; } return true; }};
- 1
数组法
复制到数组中然后,通过双指针去确认是否为回文串
递归法(还没看)
快慢指针(代码分为三大部分:1、特殊情况判断2、找出中点并反转链表。3、判断回文子串)
整个流程可以分为以下五个步骤:
- 找到前半部分链表的尾节点。
- 反转后半部分链表。
- 判断是否回文。
- 恢复链表。
- 返回结果。
执行步骤一,我们可以计算链表节点的数量,然后遍历链表找到前半部分的尾节点。
我们也可以使用快慢指针在一次遍历中找到:慢指针一次走一步,快指针一次走两步,快慢指针同时出发。当快指针移动到链表的末尾时,慢指针恰好到链表的中间。通过慢指针将链表分为两部分。
若链表有奇数个节点,则中间的节点应该看作是前半部分。
步骤二可以使用「206. 反转链表」问题中的解决方法来反转链表的后半部分。
步骤三比较两个部分的值,当后半部分到达末尾则比较完成,可以忽略计数情况中的中间节点。
步骤四与步骤二使用的函数相同,再反转一次恢复链表本身。


public boolean isPalindrome(ListNode head) { if(head == null || head.next == null) {//特殊情况 return true; } ListNode slow = head, fast = head; ListNode pre = head, prepre = null; while(fast != null && fast.next != null) {//寻找中点的同时反转一半的链表,fast.next != null用于保证该链表是偶数个数的链表 pre = slow; slow = slow.next; fast = fast.next.next; //反转链表 pre.next = prepre; prepre = pre; } if(fast != null) {//元素个数为奇数的情况 slow = slow.next; } while(pre != null && slow != null) {//判断回文子串 if(pre.val != slow.val) { return false; } pre = pre.next; slow = slow.next; } return true; }
- 1
~【完成】9. 分隔链表
725. 分隔链表 中等
方法一 计算长度
简要说说,就是先遍历一次链表计算出链表长度 nn ,然后根据 n // kn//k 就能计算出分割后每段的长度,其中前 n % kn%k 段长度比其他段长 1 。
class Solution {public: vector<ListNode*> splitListToParts(ListNode* root, int k) { int count=0;//计算有多少个结点 vector<ListNode*> table(k,nullptr); ListNode* temp=root; while(temp!=nullptr){ count++; temp=temp->next; } int carry=count%k;//carry为余数, int curr=count/k;//一共有 carry 个长度为 curr+1 的链表,剩余的链表长度都为 curr ListNode* temp1; temp=root; count=0; int count1=0; int i=1; table[0]=root; while(temp!=nullptr){ count++; temp1=temp->next; while(count1<=carry && count==curr+1&&temp->next!=nullptr){//carry个curr+1 table[i++]=temp->next; temp->next=nullptr; count1++; count=0; } while(count1<k && count==curr&&temp->next!=nullptr){//k-carry个curr table[i++]=temp->next; temp->next=nullptr; count1++; count=0; } temp=temp1; } return table; }};
- 1
双指针法
【完成】10. 链表元素按奇偶聚集
328. 奇偶链表 中等
官解
class Solution {public: ListNode* oddEvenList(ListNode* head) { if (head == nullptr) { return head; } ListNode* oddhead=head->next; ListNode* odd=oddhead; ListNode* evenhead=head; ListNode* even=head; while(odd&&odd->next){ even->next=even->next->next; even=even->next; odd->next=odd->next->next; odd=odd->next; } even->next=oddhead; return head; }};
- 1
2、树(14+2+3+10+2=31题)
递归
一棵树要么是空树,要么有两个指针,每个指针指向一棵树。树是一种递归结构,很多树的问题可以使用递归来处理。
1. 树的高度
104. 二叉树的最大深度 简单
2. 平衡树
110. 平衡二叉树 简单
3. 两节点的最长路径
543. 二叉树的直径 简单
4. 翻转树
226. 翻转二叉树 简单
5. 归并两棵树
617. 合并二叉树 简单
6. 判断路径和是否等于一个数
112. 路径55总和 简单
7. 统计路径和等于一个数的路径数量
437. 路径总和 III 中等
8. 子树
572. 另一个树的子树 简单
9. 树的对称
101. 对称5二叉树 简单
10. 最小路径
111. 二叉树的最小深度 简单
11. 统计左叶子节点的和
404. 左叶子之和 简单
12. 相同节点值的最大路径长度
687. 最长同值路径 中等
13. 间隔遍历
337. 打家劫舍 III 中等
14. 找出二叉树中第二小的节点
671. 二叉树中第二小的节点 简单
层次遍历
使用 BFS 进行层次遍历。不需要使用两个队列来分别存储当前层的节点和下一层的节点,因为在开始遍历一层的节点时,当前队列中的节点数就是当前层的节点数,只要控制遍历这么多节点数,就能保证这次遍历的都是当前层的节点。
1. 一棵树每层节点的平均数
637. 二叉树的层平均值 简单
2. 得到左下角的节点
513. 找树左下角的值 中等
前中后序遍历
1 / \ 2 3 / \ \4 5 6
- 1
- 层次遍历顺序:[1 2 3 4 5 6]
- 前序遍历顺序:[1 2 4 5 3 6]
- 中序遍历顺序:[4 2 5 1 3 6]
- 后序遍历顺序:[4 5 2 6 3 1]
层次遍历使用 BFS 实现,利用的就是 BFS 一层一层遍历的特性;而前序、中序、后序遍历利用了 DFS 实现。
前序、中序、后序遍只是在对节点访问的顺序有一点不同,其它都相同。
① 前序
void dfs(TreeNode root) { visit(root); dfs(root.left); dfs(root.right);}
- 1
② 中序
void dfs(TreeNode root) { dfs(root.left); visit(root); dfs(root.right);}
- 1
③ 后序
void dfs(TreeNode root) { dfs(root.left); dfs(root.right); visit(root);}
- 1
1. 非递归实现二叉树的前序遍历
144. 二叉树的前序遍历 中等
2. 非递归实现二叉树的后序遍历
145. 二叉树的后序遍历 简单
3. 非递归实现二叉树的中序遍历
94. 二叉树的中序遍历 简单
BST 二叉查找树
二叉查找树(BST):根节点大于等于左子树所有节点,小于等于右子树所有节点。
二叉查找树中序遍历有序。
1. 修剪二叉查找树
669. 修剪二叉搜索树 中等
2. 寻找二叉查找树的第 k 个元素
230. 二叉搜索树中第K小的元素 中等
3. 把二叉查找树每个节点的值都加上比它大的节点的值
538. 把二叉搜索树转换为累加树 中等
4. 二叉查找树的最近公共祖先
235. 二叉搜索树的最近公共祖先 简单
5. 二叉树的最近公共祖先
236. 二叉树的最近公共祖先 中等
6. 从有序数组中构造二叉查找树
108. 将有序数组转换为二叉搜索树 简单
7. 根据有序链表构造平衡的二叉查找树
109. 有序链表转换二叉搜索树 中等
8. 在二叉查找树中寻找两个节点,使它们的和为一个给定值
9. 在二叉查找树中查找两个节点之差的最小绝对值
530. 二叉搜索树的最小绝对差 简单
10. 寻找二叉查找树中出现次数最多的值
501. 二叉搜索树中的众数 简单
Trie
Trie,又称前缀树或字典树,用于判断字符串是否存在或者是否具有某种字符串前缀。
1. 实现一个 Trie
208. 实现 Trie (前缀树) 中等
2. 实现一个 Trie,用来求前缀和
677. 键值映射 中等
3、栈和队列(6题)
1. 用栈实现队列
232. 用栈实现队列 简单
2. 用队列实现栈
225. 用队列实现栈 简单
3. 最小值栈
155. 最小栈 简单
4. 用栈实现括号匹配
20. 有效的括号 简单
5. 数组中元素与下一个比它大的元素之间的距离
739. 每日温度 中等
6. 循环数组中比当前元素大的下一个元素
503. 下一个更大元素 II 中等
4、哈希表(4题)
哈希表使用 O(N) 空间复杂度存储数据,并且以 O(1) 时间复杂度求解问题。
- Java 中的 HashSet 用于存储一个集合,可以查找元素是否在集合中。如果元素有穷,并且范围不大,那么可以用一个布尔数组来存储一个元素是否存在。例如对于只有小写字符的元素,就可以用一个长度为 26 的布尔数组来存储一个字符集合,使得空间复杂度降低为 O(1)。
Java 中的 HashMap 主要用于映射关系,从而把两个元素联系起来。HashMap 也可以用来对元素进行计数统计,此时键为元素,值为计数。和 HashSet 类似,如果元素有穷并且范围不大,可以用整型数组来进行统计。在对一个内容进行压缩或者其它转换时,利用 HashMap 可以把原始内容和转换后的内容联系起来。例如在一个简化 url 的系统中 [Leetcdoe : 535. Encode and Decode TinyURL (Medium)
Leetcode,利用 HashMap 就可以存储精简后的 url 到原始 url 的映射,使得不仅可以显示简化的 url,也可以根据简化的 url 得到原始 url 从而定位到正确的资源�) / 力扣,利用 HashMap 就可以存储精简后的 url 到原始 url 的映射,使得不仅可以显示简化的 url,也可以根据简化的 url 得到原始 url 从而定位到正确的资源�)
【完成】1. 数组中两个数的和为给定值
1. 两数之和 简单
class Solution {public: vector<int> twoSum(vector<int>& nums, int target) { unordered_map<int, int> hashtable;//无序哈希表 for (int i = 0; i < nums.size(); ++i) { auto it = hashtable.find(target - nums[i]); if (it != hashtable.end()) { return {it->second, i}; } //之所以放在最后是为了只要在找到这两个数时就停止往哈希表里写入数据,节省时间和空间 hashtable[nums[i]] = i;//该哈希表的 key 为数组元素的值,val 为数组元素的下标 } return {}; }};unorder_map<int,int> hashtable;for(int i = 0;i<nums.size();i++){ auto it = hashtable.find(target-nums[i]); if(it!=hashtable.end()){ return {it->second,i}; hashtable[nums[i]]=i; }}
- 1
【完成】2. 判断数组是否含有重复元素
217. 存在重复元素 简单
第一种解法:(采用类似于计数排序的方法进行统计)
class Solution {public://计数 bool containsDuplicate(vector<int>& nums) { int min=INT_MAX; int max=INT_MIN; int k; for(int i=0;i<nums.size();i++){ if(min>nums[i]) min=nums[i]; if(max<nums[i]) max=nums[i]; } k=max-min+1; vector<int> T(k,0); for(int i=0;i<nums.size();i++){ ++T[nums[i]-min]; if(T[nums[i]-min]>1) {return true;} } return false; }};
- 1
第二种解法(哈希表法)
class Solution {public: bool containsDuplicate(vector<int>& nums) { unordered_map<int,int> hashtable;//注意hashtable不需要提前定义他的长度 for(int i=0;i<nums.size();i++){ auto it=hashtable.find(nums[i]); if(it!=hashtable.end()){ return true; } hashtable[nums[i]]=i;//注意哈希表的 key 值一般都是数组的值,因为一般查询的时候都是查询数组的某个数值,而不是数组的下标 } return false; }};
- 1
3. 最长和谐序列
594. 最长和谐子序列 简单
【完成 有一个问题没想通】4. 最长连续序列
128. 最长连续序列 困难
第一代(时间过长)
class Solution {public: int longestConsecutive(vector<int>& nums) { if(nums.size()==0){ return 0; } int max=0; unordered_set<int> Hashtable; for(int i=0;i<nums.size();i++){//创建哈希表 Hashtable.insert(nums[i]); } for(int i=0;i<nums.size();i++){ int count=0; while(Hashtable.find(nums[i]++) != Hashtable.end()){ count++; } if(max<count) max=count; } return max; }};
- 1
第二代哈希表法:(加入了条件判断,时间缩短)
class Solution {public: int longestConsecutive(vector<int>& nums) { if(nums.size()==0){ return 0; } int max=0; unordered_set<int> Hashtable; for(int i=0;i<nums.size();i++){//创建哈希表 Hashtable.insert(nums[i]); } for(int i=0;i<nums.size();i++){ int count=0; if(Hashtable.find(nums[i]-1) != Hashtable.end()) continue;//加入了判断,缩短时间 while(Hashtable.find(nums[i]++) != Hashtable.end()){ count++; } if(max<count) max=count; } return max; }};
- 1
第三种,别人写的,并查集,还没搞懂(别人的评论:第一种方法不是并查集吧,只是用递归重写了for循环。)
class Solution {public: unordered_map<int,int> a,b; int find(int num){ return a.count(num) ? a[num] = find(a[num]) : num;//判断哈希表中是否存在 x 这个数,存在的话啊 a[x] 就等于 a[x] 的下标,不存在的话 a[x] = x } int longestConsecutive(vector<int>& nums) { for(auto num:nums)//遍历 nums 数组 a[num]=num+1; int count=0; for(auto low:nums){//遍历哈希表 int high = find(low+1); //是否存在后驱元素 count=max(count,high-low); } return count; }};
- 1
第四种:学习了力扣官解第二个for使用哈希表遍历,快了几十倍不止
class Solution {public: int longestConsecutive(vector<int>& nums) { unordered_set<int> Hashtable; for(auto num:nums){//创建哈希表 Hashtable.insert(num); } int longest=0; for(auto num:Hashtable){ int c=0; if(Hashtable.count(num-1)) continue;//加入了判断,缩短时间 while(Hashtable.count(num)){ num+=1; c+=1; } if(longest<c) longest=c; } return longest; }};
- 1
5、字符串(9题)
【无】1. 字符串循环移位包含
[编程之美 3.1](https://github.com/CyC2018/CS-Notes/blob/master/notes/Leetcode 题解 - 字符串.md#)
【无】2. 字符串循环移位
[编程之美 2.17](https://github.com/CyC2018/CS-Notes/blob/master/notes/Leetcode 题解 - 字符串.md#)
【无】3. 字符串中单词的翻转
[程序员代码面试指南](https://github.com/CyC2018/CS-Notes/blob/master/notes/Leetcode 题解 - 字符串.md#)
【完成】4. 两个字符串包含的字符是否完全相同
242. 有效的字母异位词 简单
用冒泡排序会超时:
class Solution { //快速排序public: void mySort(string &s){ for(int i=0;i<s.size();i++){ for(int j=0;j<s.size()-i-1;j++){ if(s[j]>s[j+1]){ char temp; temp=s[j+1]; s[j+1]=s[j]; s[j]=temp; } } } } bool isAnagram(string s, string t) { sort(s.begin(), s.end()); sort(t.begin(), t.end()); if(s.size()!=t.size()) return false; int ptr1=0,ptr2=0; while(ptr1<s.size() && ptr1<s.size()){ if(s[ptr1]!=t[ptr2]){ return false; } ptr1++; ptr2++; } return true; }};
- 1
排序官解
class Solution {public: bool isAnagram(string s, string t) { if (s.length() != t.length()) { return false; } sort(s.begin(), s.end()); sort(t.begin(), t.end()); return s == t; }};
- 1
哈希表法:(哈希表采用的数据结构不一定是 set 或者 map)
//官解class Solution {public: bool isAnagram(string s, string t) { if (s.length() != t.length()) { return false; } vector<int> table(26, 0); for (auto& ch: s) { table[ch - 'a']++; } for (auto& ch: t) { table[ch - 'a']--; if (table[ch - 'a'] < 0) { return false; } } return true; }};
- 1
【哈希表法】
class Solution {public: bool isAnagram(string s, string t) { vector<int> table(26,0); if(s.size()!=t.size()){ return false; } for(char sl:s){ table[sl-'a']++; } for(char tl:t){ table[tl-'a']--; if(table[tl-'a']<0) return false; } return true; }};
- 1
【完成】5. 计算一组字符集合可以组成的回文字符串的最大长度
409. 最长回文串 简单
class Solution {public://哈希表法 int longestPalindrome(string s) { unordered_map<char,int> table; int ans=0; for(int i=0;i<s.length();i++){ table[s[i]]++; } for(auto p:table){ int num=p.second; ans+=num/2*2;//这个操作是为了防止num的是数量是大于1的奇数,如3,可以取2,多余的1个可以后面判断是否要加上 if (num % 2 == 1 and ans % 2 == 0)//这个if只会执行一次,因为只要加上一次单独的奇数个就会导致ans永远是奇数,因为上面加上的 num/2*2永远是偶数 ++ans; } return ans; }};
- 1
【完成】6. 字符串同构
205. 同构字符串 简单

class Solution {public: bool isIsomorphic(string s, string t) { unordered_map<char,char> table; string ans=""; ans.resize(s.length(),0);//没有这一步,不能成功构造 for(int i=0;i<s.length();i++){ table[s[i]]=t[i]; } for(int i=0;i<s.length();i++){ ans[i]=table[s[i]]; } if(ans==t){ for(int i=0;i<s.length();i++){ table[t[i]]=s[i]; } for(int i=0;i<s.length();i++){ ans[i]=table[t[i]]; } return ans==s?true:false; } return false; }};
- 1
~【完成】7. 回文子字符串个数
647. 回文子串 中等
中心拓展法
class Solution {public: int countSubstrings(string s) { int num = 0; int n = s.size(); for(int i=0;i<n;i++)//遍历回文中心点 { for(int j=0;j<=1;j++)//j=0,中心是一个点,j=1,中心是两个点 { int l = i; int r = i+j; while(l>=0 && r<n && s[l--]==s[r++])num++; } } return num; }};
- 1
动态规划(未看)
【完成】8. 判断一个整数是否是回文数
9. 回文数 简单
普通解法(转字符串)
class Solution {public: bool isPalindrome(int x) { if(x<0) return false; string temp=to_string(x); string ans=to_string(x); reverse(temp.begin(),temp.end()); return temp==ans?true:false; }};
- 1
进阶解法—数学解法
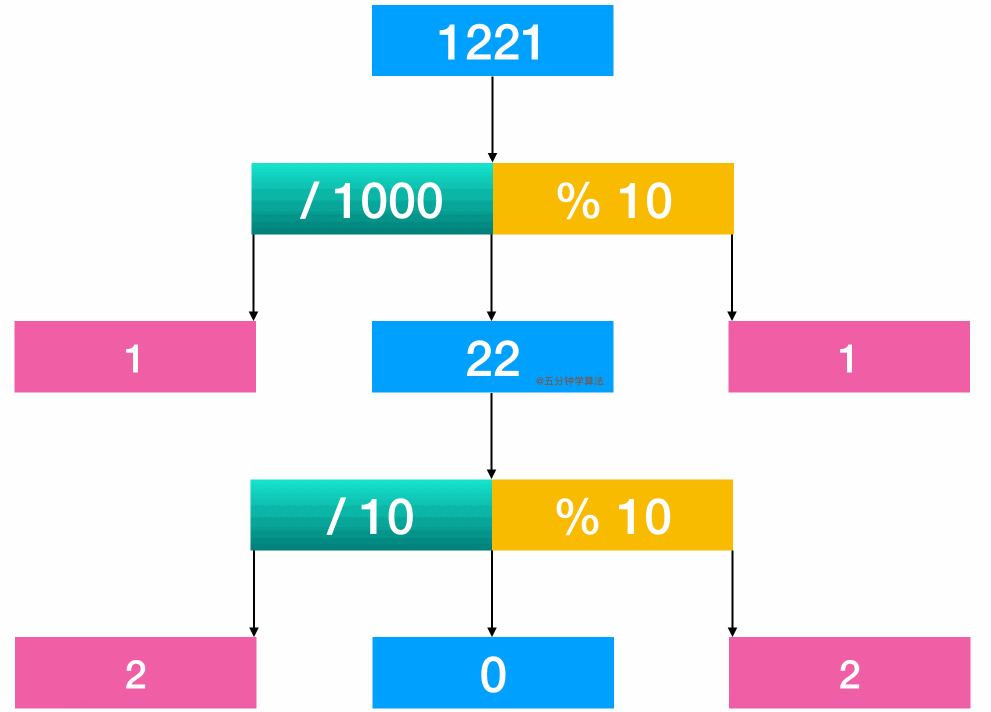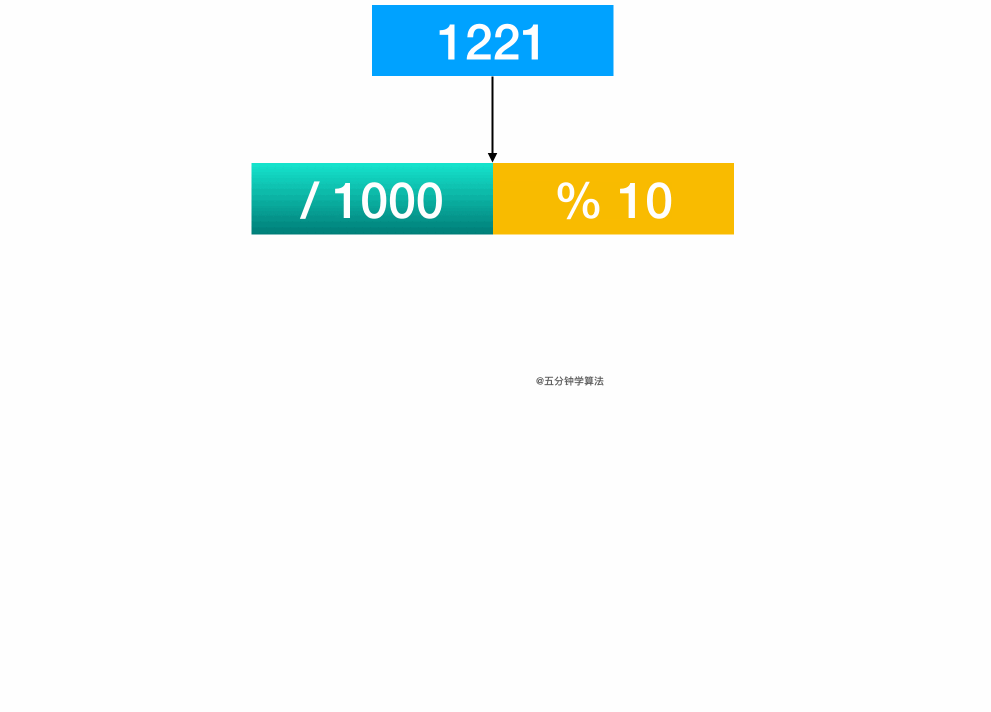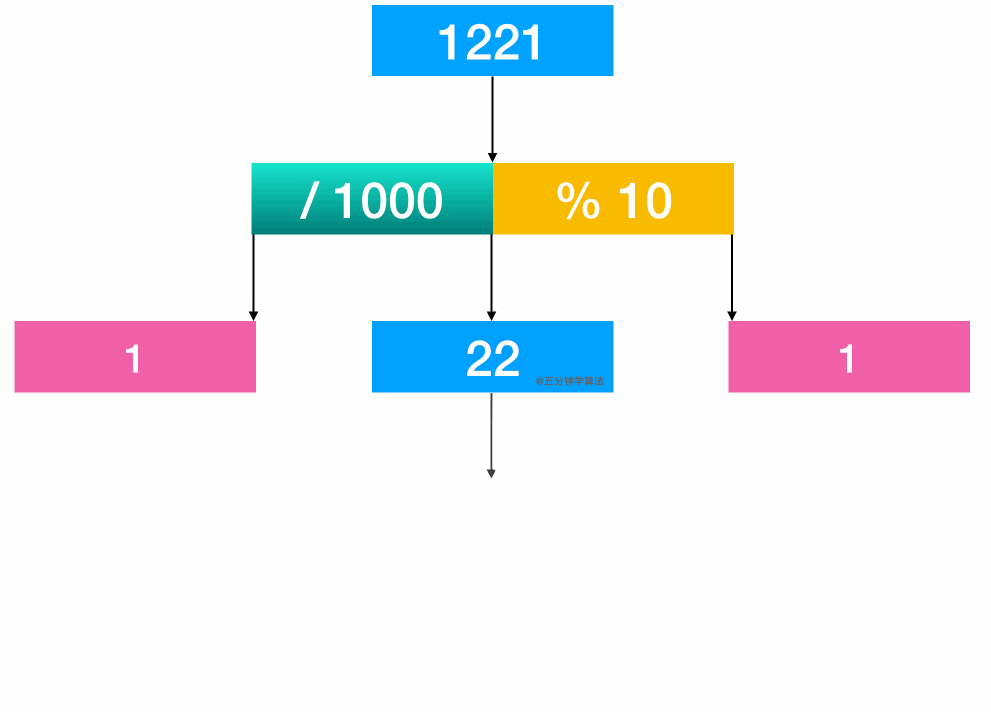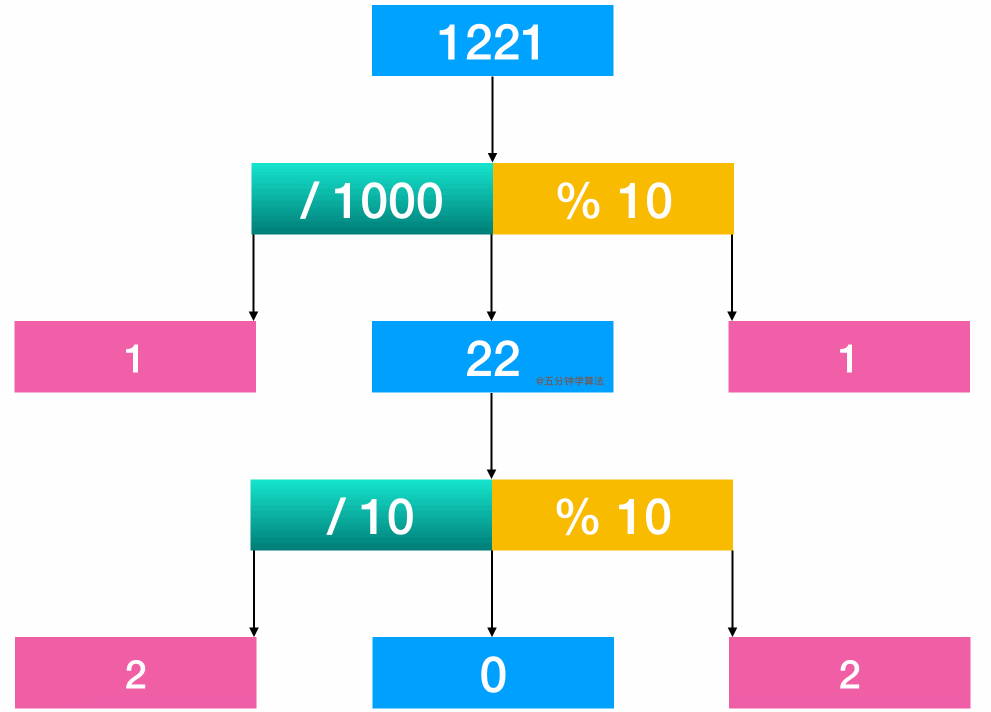
class Solution {public: bool isPalindrome(int x) { if(x<0) return false; int div=1; while(x/div>=10) div*=10;//注意不要少了等号 while(x>0){ int l=x / div; int r=x % 10; if(l!=r) return false; x=(x % div) / 10; div=div / 100; } return true; }};
- 1
解法三:进阶解法—巧妙解法
9. 统计二进制字符串中连续 1 和连续 0 数量相同的子字符串个数
696. 计数二进制子串 简单
6、数组与矩阵(12题)
【完成】1. 把数组中的 0 移到末尾
283. 移动零 简单.
【自己写的】
class Solution {public: void moveZeroes(vector<int>& nums) { int count=0; for(int i=0;i<nums.size();i++){ if(nums[i]!=0){ nums[count++]=nums[i]; } } for(;count<nums.size();count++){ if(nums[count]!=0) nums[count]=0; } }};
- 1
2. 改变矩阵维度
566. 重塑矩阵 简单
3. 找出数组中最长的连续 1
485. 最大连续 1 的个数 简单
4. 有序矩阵查找
240. 搜索二维矩阵 II 中等
5. 有序矩阵的 Kth Element
378. 有序矩阵中第 K 小的元素 中等
6. 一个数组元素在 [1, n] 之间,其中一个数被替换为另一个数,找出重复的数和丢失的数
645. 错误的集合 简单
7. 找出数组中重复的数,数组值在 [1, n] 之间
287. 寻找重复数 中等
8. 数组相邻差值的个数
667. 优美的排列 II 中等
9. 数组的度
697. 数组的度 简单
10. 对角元素相等的矩阵
766. 托普利茨矩阵 简单
11. 嵌套数组
565. 数组嵌套 中等
12. 分隔数组
769. 最多能完成排序的块 中等
7、图(1+2+1=4题)
8、位运算(13题)
0. 原理
基本原理
基本原理
0s 表示一串 0,1s 表示一串 1。
x ^ 0s = x x & 0s = 0 x | 0s = xx ^ 1s = ~x x & 1s = x x | 1s = 1sx ^ x = 0 x & x = x x | x = x
- 1
利用 x ^ 1s = ~x 的特点,可以将一个数的位级表示翻转;利用 x ^ x = 0 的特点,可以将三个数中重复的两个数去除,只留下另一个数。
1^1^2 = 2
- 1
利用 x & 0s = 0 和 x & 1s = x 的特点,可以实现掩码操作。一个数 num 与 mask:00111100 进行位与操作,只保留 n········um 中与 mask 的 1 部分相对应的位。
01011011 &00111100--------00011000
- 1
利用 x | 0s = x 和 x | 1s = 1s 的特点,可以实现设值操作。一个数 num 与 mask:00111100 进行位或操作,将 num 中与 mask 的 1 部分相对应的位都设置为 1。
01011011 |00111100--------01111111
- 1
位与运算技巧
n&(n-1) 去除 n 的位级表示中最低的那一位 1。例如对于二进制表示 01011011,减去 1 得到 01011010,这两个数相与得到 01011010。
01011011 &01011010--------01011010
- 1
n&(-n) 得到 n 的位级表示中最低的那一位 1。-n 得到 n 的反码加 1,也就是 -n=~n+1。例如对于二进制表示 10110100,-n 得到 01001100,相与得到 00000100。
10110100 &01001100--------00000100
- 1
n-(n&(-n)) 则可以去除 n 的位级表示中最低的那一位 1,和 n&(n-1) 效果一样。
移位运算
>> n 为算术右移,相当于除以 2n,例如 -7 >> 2 = -2。
11111111111111111111111111111001 >> 2--------11111111111111111111111111111110
- 1
>>> n 为无符号右移,左边会补上 0。例如 -7 >>> 2 = 1073741822。
11111111111111111111111111111001 >>> 2--------00111111111111111111111111111111
- 1
<< n 为算术左移,相当于乘以 2n。-7 << 2 = -28。
11111111111111111111111111111001 << 2--------11111111111111111111111111100100
- 1
(x >> i) & 1 得到 xx 的第 i 个二进制位
mask 计算
要获取 111111111,将 0 取反即可,~0。
要得到只有第 i 位为 1 的 mask,将 1 向左移动 i-1 位即可,1<<(i-1) 。例如 1<<4 得到只有第 5 位为 1 的 mask :00010000。
要得到 1 到 i 位为 1的 mask,(1<<i)-1 即可,例如将 (1<<4)-1 = 00010000-1 = 00001111。
要得到 1 到 i 位为 0 的 mask,只需将 1 到 i 位为 1 的 mask 取反,即 ~((1<<i)-1)。
总结
1、错位异或
2、各位二进制位累加进行余数计算,%3
3、分治
4、一些数学思想:
偶数 n 的二进制位1等于 n/2 偶数的 1 的个数,奇数 1 的个数等于前一个偶数的 1 的个数
4的幂次方 n % 3 == 1
2的幂次方只有一个1
加法等于 ^ + & 运算
【完成】1. 统计两个数的二进制表示有多少位不同
461. 汉明距离 简单
class Solution {public: int hammingDistance(int x, int y) { int temp = x^y;//temo中的1就是xy中不同的元素的位置 int count=0; while(temp>0){ count++; temp&=(temp-1); } return count; }};
- 1
【完成】2. 数组中唯一一个不重复的元素
136. 只出现一次的数字 简单
class Solution {public: int singleNumber(vector<int>& nums) { int ans=nums[0]; for(int i=1;i<nums.size();i++){ ans^=nums[i]; } return ans; }};
- 1
【完成】3. 找出数组中缺失的那个数
268. 丢失的数字 简单
四种方法:
**哈希表法:**存入数字,然后遍历0~n,一一去set中查找是否存在
**数学法:**将0~n累加起来,一边加一边减
**排序法:**排序后一一对比
**位运算法:**将0~n以及数组中出现的所有数字进行异或,最后的值就是缺的值,因为其他数都出现了两次,0和所有非0数异或都为该非0数
【完成】4. 数组中不重复的两个元素
260. 只出现一次的数字 III 中等
排序法
class Solution {public://排序法 vector<int> singleNumber(vector<int>& nums) { sort(nums.begin(),nums.end()); int n=nums.size(); int a=0; vector<int> ans(2,0); if(nums[n-2]!=nums[n-1]) ans[a++]=nums[n-1]; for(int i=0;i<nums.size()-1;){ if(nums[i]!=nums[i+1]){ ans[a++]=nums[i]; i++; } else i+=2; } return ans; }};
- 1
位运算法
分组异或:两个不同的数必定被分到不一样的组,因为


class Solution {public: vector<int> singleNumber(vector<int>& nums) { long div=0;//用于分组的变量,取0是因为0异或所有数都为它本身 for(int num:nums){ div^=num; } div&=(-div);//取div最低位的1 int a=0,b=0; for(int num:nums){ if(div&num){//num的最后一位为1 a^=num; } else b^=num; } return {a,b}; }};
- 1
哈希表法
class Solution {public://哈希表法 int singleNumber(vector<int>& nums) { unordered_map<int,int> freq; for(int num:nums){ ++freq[num];//存入哈希表 } for (auto [num,count] :freq){//注意这种特殊的遍历方式 if(count==1){ return num; } } return 0; }};
- 1
位运算法
这个算法的思想就是,出现了三次,那么将每个数的每个对应的二进制位的相加,如果%3有余数,那么就是表示只出现了一次的那个数的那个二进制位那个位置是1,因此这种算法对于出现了 4 5 6 7…10 11次去找那个只出现了一次的数的题目都适用
class Solution {public: int singleNumber(vector<int>& nums) { int ans=0; for(int i=0;i<32;i++){ int total=0; for(int num:nums){ total += (num>>i)&1; } if(total % 3){ ans|=(1<<i); } } return ans; }};
- 1
【完成】5. 翻转一个数的比特位
190. 颠倒二进制位 简单
分治法(较难想到)
class Solution {private: const uint32_t M1 = 0x55555555; // 01010101010101010101010101010101 const uint32_t M2 = 0x33333333; // 00110011001100110011001100110011 const uint32_t M4 = 0x0f0f0f0f; // 00001111000011110000111100001111 const uint32_t M8 = 0x00ff00ff; // 00000000111111110000000011111111public: uint32_t reverseBits(uint32_t n) { n = n >> 1 & M1 | (n & M1) << 1; n = n >> 2 & M2 | (n & M2) << 2; n = n >> 4 & M4 | (n & M4) << 4; n = n >> 8 & M8 | (n & M8) << 8; return n >> 16 | n << 16; }};
- 1
位运算法
class Solution {public: uint32_t reverseBits(uint32_t n) { int ans=0; int temp=0; for(int i=0;i<32;i++){ temp=(n>>i)&1; //得到从右往左第 i 位的 0 或者 1 ans|=temp<<(32-i-1); //将这个 1 移动到ans的从左往右第 i 位 } return ans; }};
- 1
【无】6. 不用额外变量交换两个整数
[程序员代码面试指南 :P317](https://github.com/CyC2018/CS-Notes/blob/master/notes/Leetcode 题解 - 位运算.md#)
【完成】7. 判断一个数是不是 2 的 n 次方
231. 2的幂 简单
位运算法
//自己写的class Solution {public: bool isPowerOfTwo(int n) { if(n<0) return false; //如果是负数一定不会是2的幂次方 int total=0; for(int i=0;i<32;i++){ //统计 n 的二进制数中有几个1 if(n>>i&1) total++; } if(total==1) return true; //如果是2的幂次方,那么二进制数一定只有一个 1 else return false; }};
- 1
//官解1class Solution {public: bool isPowerOfTwo(int n) { return n > 0 && (n & (n - 1)) == 0; }};//官解2class Solution {public: bool isPowerOfTwo(int n) { return n > 0 && (n & -n) == n; }};
- 1
数学法
class Solution {private: static constexpr int BIG = 1 << 30;public: bool isPowerOfTwo(int n) { return n > 0 && BIG % n == 0; }};
- 1
【完成】8. 判断一个数是不是 4 的 n 次方
342. 4的幂 简单
傻瓜式求解:迭代除4(别人写的)
class Solution { public boolean isPowerOfFour(int n) { if (n < 1) return false; while (n % 4 == 0) { n /= 4; } return n == 1; }}
- 1
取模法
思路:
1、排除 n<=0 的情况,易错点,顺序不能写错,因为是按照写的顺序依次判断条件是否成立的
2、保证该数是2的幂次方,通过保证2进制数只有一个 1, n&(n-1)== 0 (去除了最后一位 1 后就没有 1 了说明这个二进制数只有一个)
3、如果是4的幂次方,对3取模的结果一定是1,(如果 n 是 2 的幂却不是 4的幂,那么它可以表示成 4x×2 的形式,此时它除以 3 的余数一定为 2)。
这段理解非常重要:比如(3+1) (3+1)=9+3+3+1,该数 mod3 一定等于1,即余数为1,那么(3+1) (3+1)* 2的余数也就是前面余数的两倍,也就是2 **
class Solution {public: bool isPowerOfFour(int n) { //注意(n&(n-1))==0外面的括号不能删 return n > 0 && (n & (n - 1)) == 0 && n % 3 == 1;//关键就是这个 n&(n-1) ,可以排除奇数,因为7%3=1 }};
- 1
位运算法
思路:
1、排除 n<=0 的情况,易错点,顺序不能写错,因为是按照写的顺序依次判断条件是否成立的
2、保证该数是2的幂次方,通过保证2进制数只有一个 1, n&(n-1)== 0 (去除了最后一位 1 后就没有 1 了说明这个二进制数只有一个)
3、并且这个1出现在偶数位上 0xaaaaaaaa & n==0
class Solution {public: bool isPowerOfFour(int n) { return n > 0 && (n & (n - 1)) == 0 && (n & 0xaaaaaaaa) == 0; //n&(n-1)是为了排除奇数的可能,因为 101 & 010 == 0 }};
- 1
【完成】9. 判断一个数的位级表示是否不会出现连续的 0 和 1
693. 交替位二进制数 简单
转字符串法
错位异或法
class Solution {public: bool hasAlternatingBits(int n) { unsigned int t = (n ^ (n>>1)); return (t & (t+1)) == 0;//t&(t-1)用于消除最低位级的1 }};
- 1
10. 求一个数的补码
476. 数字的补数 简单
【完成(还需要再看)】11. 实现整数的加法
371. 两整数之和 中等
无符号数概念
位运算法
class Solution {public: int getSum(int a, int b) { if (b == 0) return a; return getSum(a^b, (unsigned int)(a&b)<<1);//注意()括号中的强制类型转换 }};
- 1
12. 字符串数组最大乘积
318. 最大单词长度乘积 中等
【完成】13. 统计从 0 ~ n 每个数的二进制表示中 1 的个数
338. 比特位计数 简单
位运算法(遍历,暴力解法)
class Solution {public: vector<int> countBits(int n) { vector<int> ans(n+1,0); for(int i=0;i<=n;i++){ int total=0; for(int j=0;j<32;j++){ if(i>>j&1){ total++; } } ans[i]=total; } return ans; }};
- 1
位运算法:(这种方法有点傻瓜式,相当于预先找完规律再做题)
class Solution {public: vector<int> countBits(int n) { vector<int> ans(n+1,0); ans[0]=0; for(int i=1;i<=n;i++){ if(1&i){ //判断是否为偶数 ans[i]=ans[i-1]+1; //奇数的1的数量比它前面的偶数的1的数量多1 } else{ ans[i]=ans[i/2];//偶数的1的数量一定和它二分之一的1 的个数是一样的 } } return ans; }};
- 1
十大排序算法
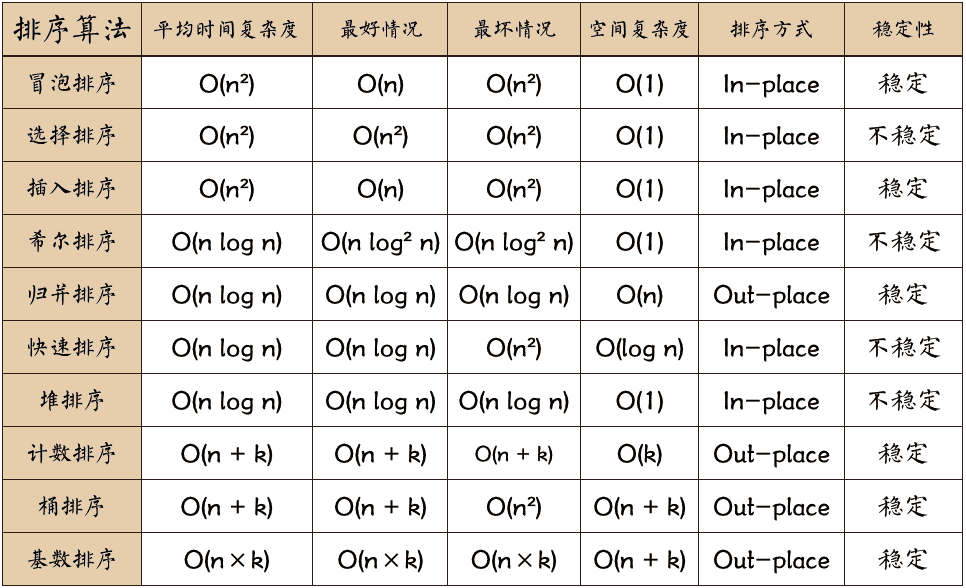
注:
- 【2 for】冒泡、选择、插入都是2个for,一个用于控制将排序范围不断缩小,不去影响已经排好序的序列
- 【3 for, temp】希尔排序是3个for,和插入排序相比多了一个控制d的大小的for
- 【2 for 、2 while、3 ptr】归并排序是2个for,一个控制所需排序数组中的元素全部拷贝到辅助数组中,另一个for对数组进行归并操作,还有两个while,将两个待归并子序列中多余长度的部分之间复制到原数组中
- 【2 while、2 ptr】快速排序,写起来其实比归并排序简单
- 注意:归并算法和快速排序算法中都运用了递归的思想,所以在书写时的那个排序的主函数中内容都应该放入一个 if(low<high){} 的条件判断函数体中,不然会发生栈溢出的情况
- 【3 for】堆排序,主函数中两个for:一个 for 是用于建立大根堆, 一个for用于实现排序过程,保证已经排序完的序列范围不再参与排序,并且重新将未排序序列变成大根堆,HeapAdject 中的for 用于调整根节点和孩子节点的位置,并且控制下坠,也就是往下验证更换位置后是否还是大根堆
一、基于比较的排序
1、冒泡排序(两两交换)
(一个一个对比,每次移动一个未排序序列中的最大值到最后)
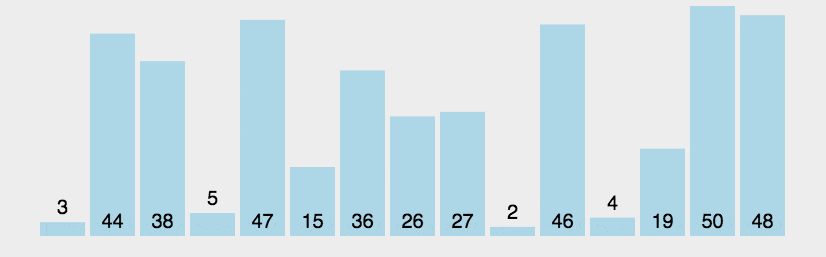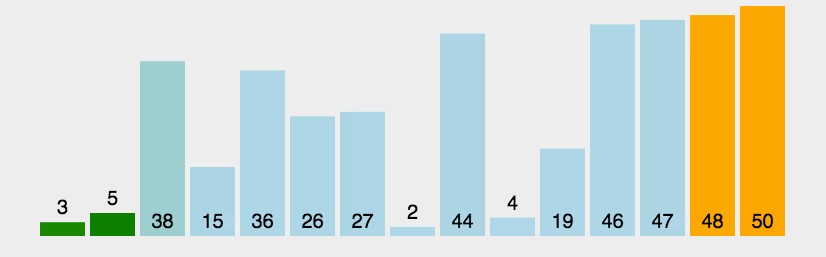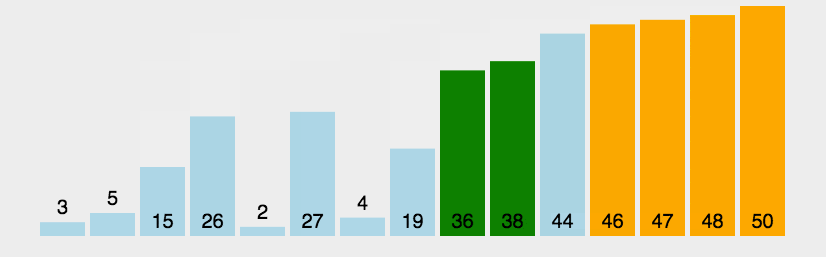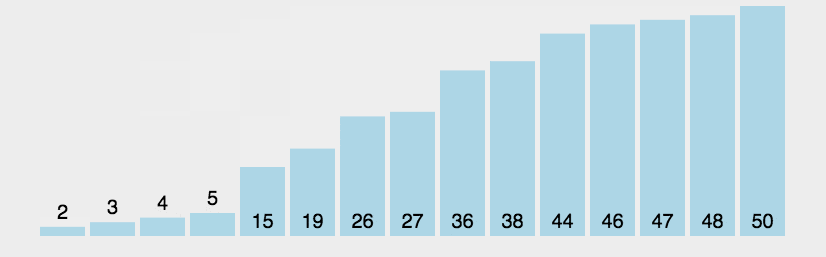
auto n=nums.size();int i,j;for(i=0;i<n;i++){ //用于固定最后的已经冒泡冒上来的数字,通过i的增加逐渐减少j循环中对比交换的过程次数 for(j=0;j<n-i-1;j++){ if(nums[j]<nums[j+1]) swap(nums[j],nums[j+1]); } }
- 1
2、选择排序(选最小去对调)
每一趟在待排序元素中选取关键字最小(或最大)的元素加入有序子序列
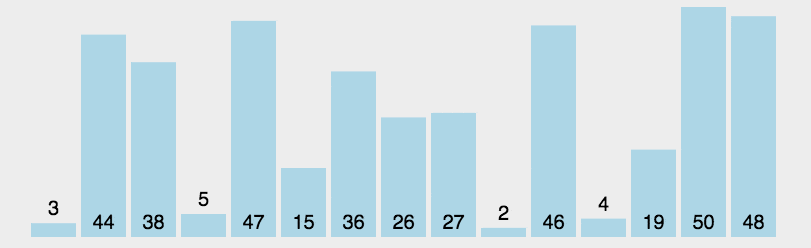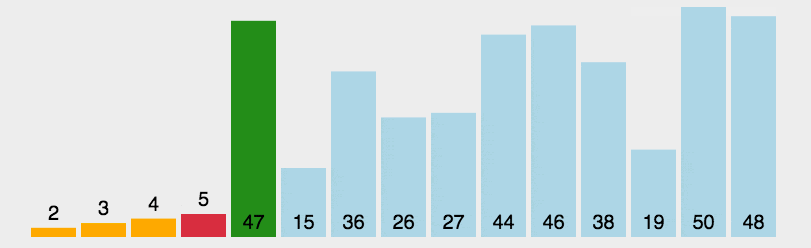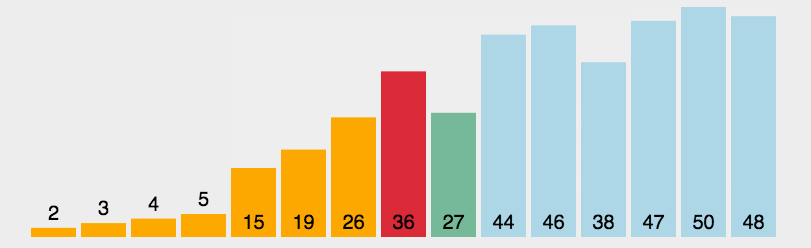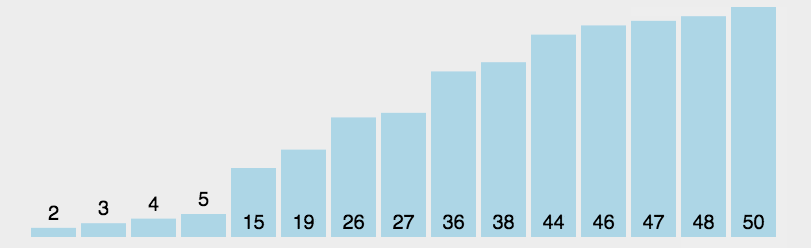
auto n = nums.size();int i,j,relmax;for(i=0;i<n-1;i++){ relmax=n-i-1;//这个是易错点 for(j=0;j<n-i-1&&nums[relmax]<nums[j];j++){ relmax=j; } swap(nums[n-i-1],nums[relmax]);}return nums;
- 1
3、插入排序(插纸牌)
序列分两段,已排序和未排序,每次将未排序序列中的第一个值记录下来,然后把已排序序列中的比这个值大的数都往后移一位,再把该值插入到前面空出来的位置中
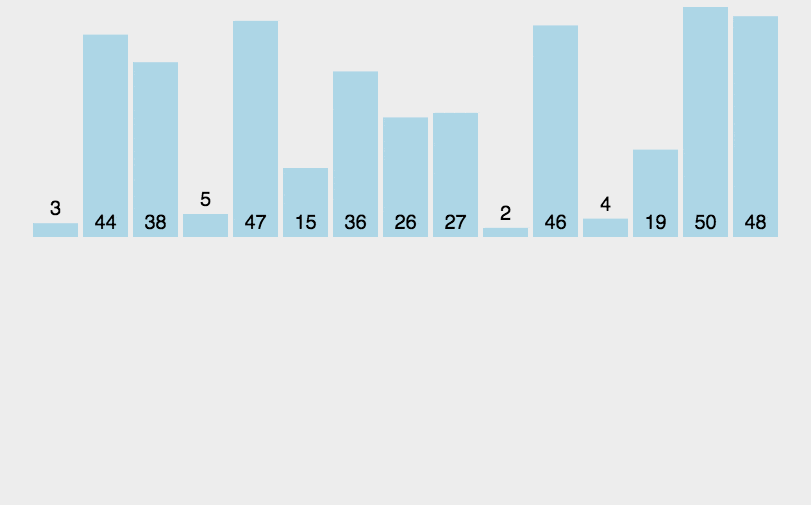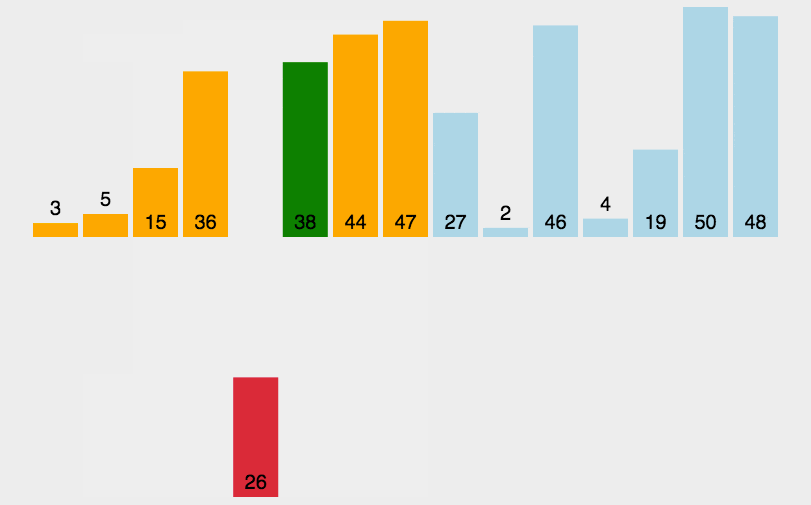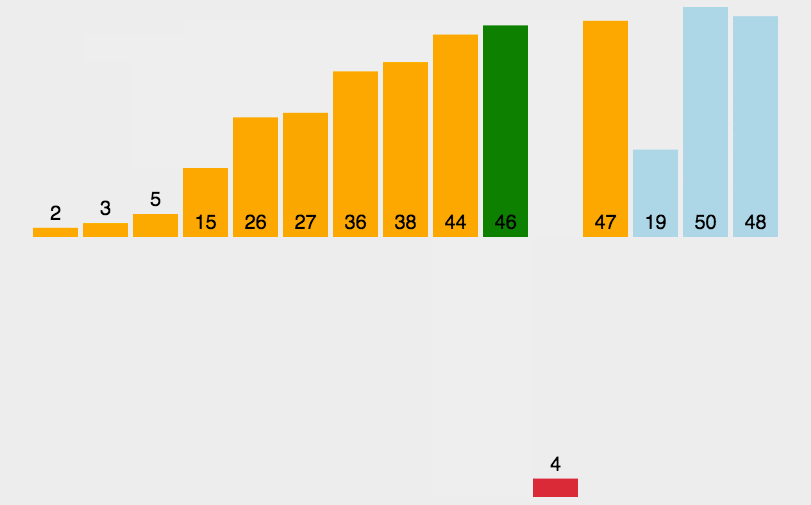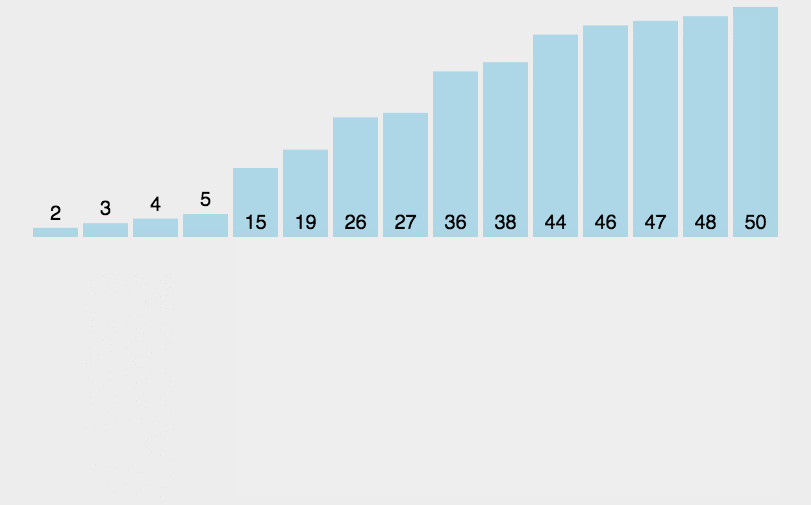
插入排序的思路:
1、先用一个循环控制前面已经排好序的序列的范围
auto n=nums.size();int i,j,temp;for(i=1;i<n;i++){// 1 }
- 1
2、将该序列后的一个值保存在value中
auto n=nums.size();int i,j,temp;for(i=1;i<n;i++){// 1 temp=nums[i];// 2}
- 1
3、再用一个for循环去把已经排序完成的序列中比 temp 大的数依次往后移一位
auto n=nums.size();int i,j,temp;for(i=1;i<n;i++){// 1 temp=nums[i];// 2 for(j = i-1,j >= 0 && temp < nums[j];j--){// 3 nums[j+1]=nums[j]; }}
- 1
4、最后将所需要插入的 temp 中的值插入到 j+1 处
auto n=nums.size(); int i,j,temp;for(i=1;i<n;i++){// 1 temp=nums[i];// 2 for(j = i-1;j >= 0 && temp < nums[j];j--){// 3 其中将判断条件 temp < nums[j]和j >= 0写在一起就等价于下面注释所写 nums[j+1]=nums[j]; } nums[j+1]=temp;// 4}return nums;//等价于下面的代码,如果不满足 nums[j]>temp 会直接执行外部循环,而不是一直等到j不在 >=0 的时候结束循环 if(temp < nums[j]){ for(j = i-1,j >= 0;j--){ nums[j+1]=nums[j]; }}//之所以采用这种写法是因为插入排序时前面已经排序完成的序列是有序的,一旦一个数 nums[j]<temo ,则更前面的数也一定是小于temp的
- 1
//错误写法auto n=nums.size();int i,j,temp;for(i=1;i<n;i++){ temp=nums[i]; for(j=i-1;j>=0;j--){ if(temp<nums[j])//不能将条件判断放里面 nums[j+1]=nums[j]; } nums[j+1]=temp;}return nums;
- 1
4、希尔排序(部分有序—>全局有序)
其实说到底就是在原来插入排序的基础上加入了一个控制序列分段的d参数
//本来想写另一种更加好理解的希尔算法程序,但是太过复杂,没必要auto n=nums.size();int i,j,temp,d;for(d=n/2;d>=1;d=d/2){ for(i=0;i<n;i+=d){//该循环用于分割多个子序列,d为多少,就有多少个子序列,特殊情况:当d等于1时,有n个子序列 }}
- 1
以下程序较为简洁,但是理解需要绕一下(有三个for)
auto n=nums.size();int i,j,temp,d;for(d=n/2;d>=1;d=d/2){//第一个for用于间距d的增减 for(i=d;i<n;i++){//第二个for用于控制多个子序列之间的切换轮流进行排序 temp=nums[i]; for(j=i-d;j >=0 && temp < nums[j];j-=d){//第三个for用于保证每个子序列中某个需要插入的数能依次与前面的数进行比较大小 nums[d+j]=nums[j]; } nums[d+j]=temp; }}return nums;
- 1
5、归并排序(先分再合)
采用递归的方式将一个序列逐步变成两两比较的状态
注意:
1、另外创建的数组 B 不能放到需要递归的函数中
2、遍历效率
for(k=low;k<=high;k++){ B[k]=A[k];}//上面的这个遍历会比下面的遍历方式快,下面的遍历会超时for(int a:A){ B[k++]=a;}
- 1
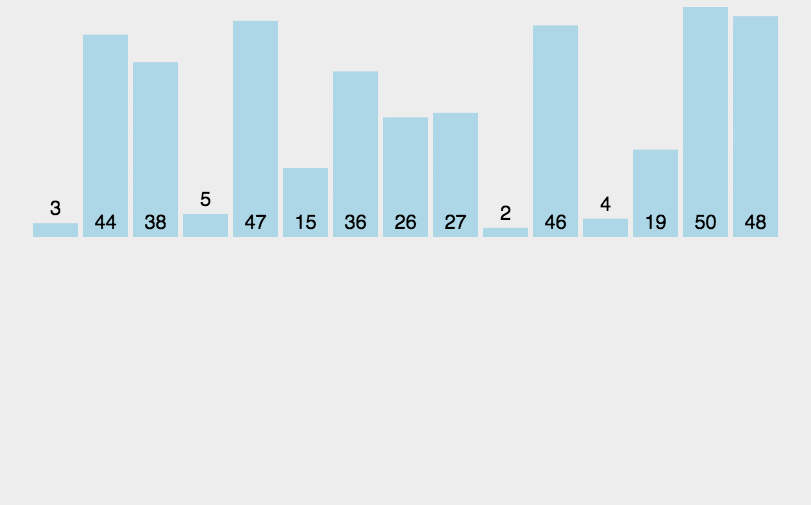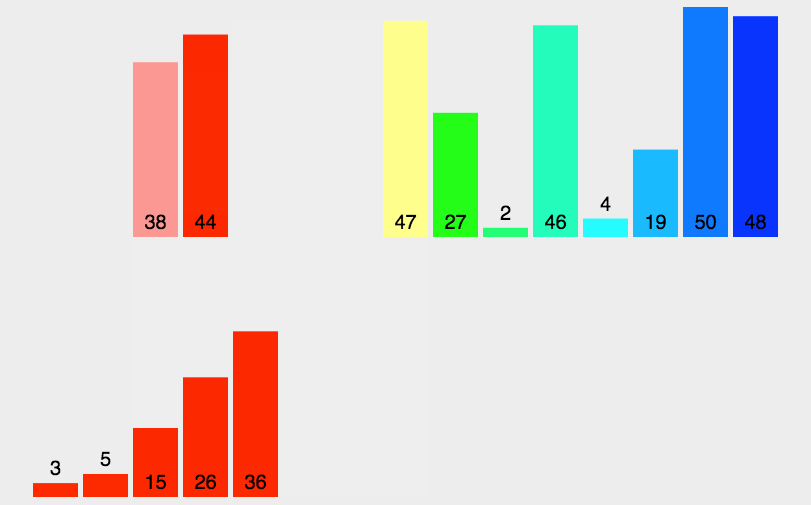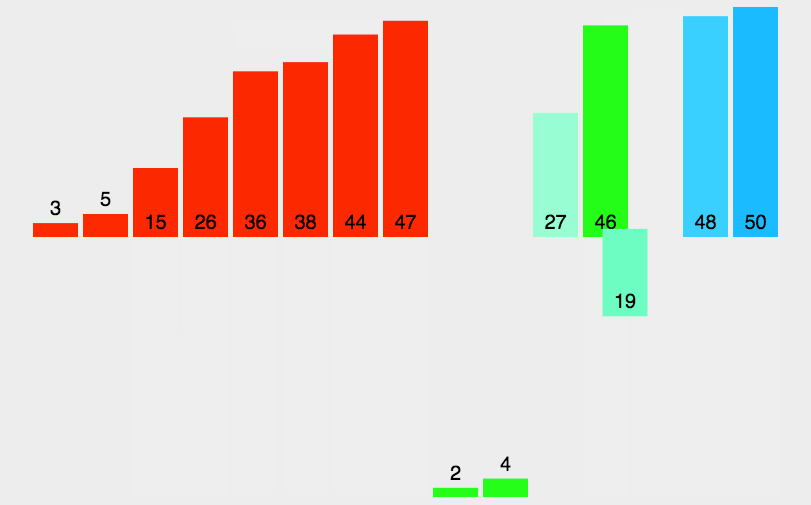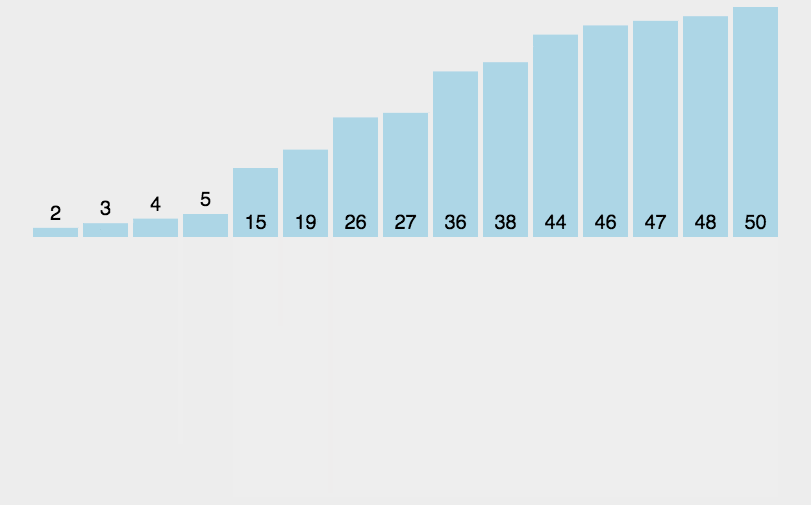
auto n=nums.size();int *B=(int *)malloc(n*sizeof(int));//这步注意指针//该函数是用来给后面的递归函数调用的void merge(int A[],int low ,int mid,int high){ int i,j,k,B[]; for(k=low;k<=high;k++){//第一步,先将原数组low和high之内的元素全部复制到新数组B中 B[k]=A[k]; } for(i=low,j=mid+1,k=i;i<=mid&&j<=high;k++){//注意此处的k=i保证原数组序列和新归并的序列起点在大的整体数组中的位置一样 if(B[i]<=B[j]) A[k]=B[i++]; else A[k]=B[j++]; } //将数组中剩余的元素复制到A数组中 while(i<=mid){A[k++]=B[i++];} while(j<=high){A[k++]=B[j++];}}//mergeSOrtvoid mergeSort(int A[],int low,int high){ if(low<high){ int mid=(low+high)/2; mergeSort(A,low,mid);//左边的序列排序//注意A后面不要加[] mergeSort(A,mid+1,high); merge(A,low,mid,high); }}
- 1
力扣解题版:
class Solution {private: vector<int> temp;public: void mergeSort(vector<int>& nums,int low ,int high){//该处的vector<int>& nums注意 if(low<high){//这个位置是易错点 int mid=(low+high)/2; mergeSort(nums,low,mid); mergeSort(nums,mid+1,high); int i,j,k; for(k=low;k<=high;k++){ temp[k]=nums[k]; } for(i=low,j=mid+1,k=i;i<=mid&&j<=high;k++){ if(temp[i]<=temp[j]) nums[k]=temp[i++]; else nums[k]=temp[j++]; } while(i<=mid){nums[k++]=temp[i++];} while(j<=high){nums[k++]=temp[j++];} }} vector<int> sortArray(vector<int>& nums) { temp.resize((int)nums.size(), 0);//设置temp的长度,第二个参数的初始值 mergeSort(nums,0,(int)nums.size() - 1); return nums; }};
- 1
6、快速排序(选枢纽,分前后序列)
双指针,low和high
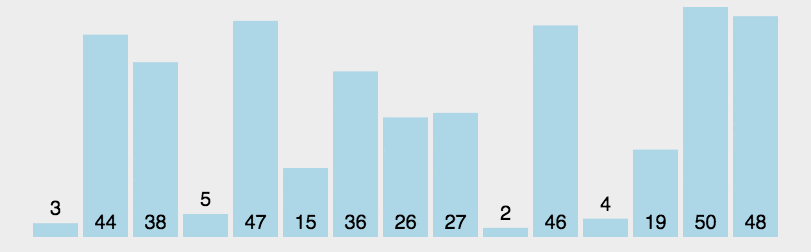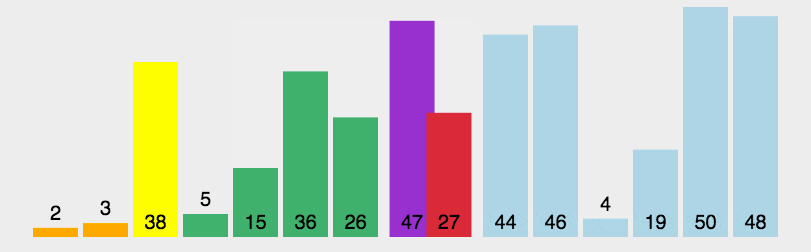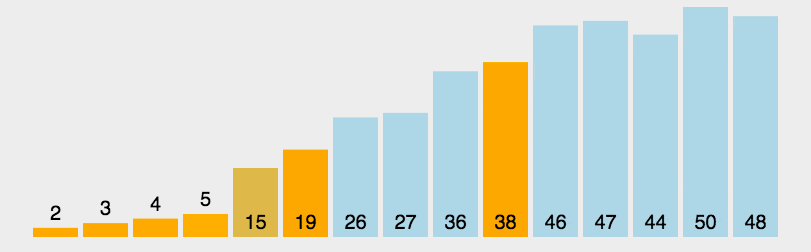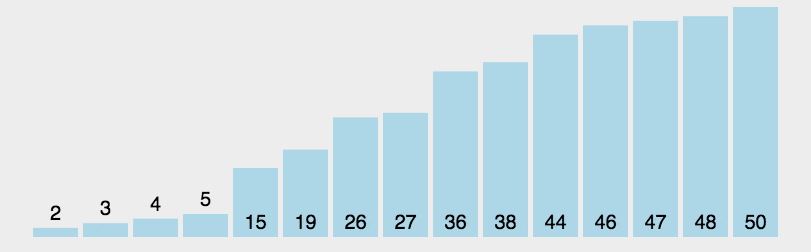
int partition(int nums[],int low,int high){ //int pivot=low;//这种写法是错的,后面low所指向的元素很快会被取代 int pivot=nums[low]; while(low<high){ //这步的作用是,当high所指元素比枢纽元素大时,high就--(当时一开始错的就是这一步) while(low<high&&nums[high]>=pivot) high--; nums[low]=nums[high]; while(low<high&&nums[low]<pivot) low++; nums[high]=nums[low]; } } nums[low]=pivot; return low;}void QuickSort(int A[],int low,int high){ if(low<high){ int pivot=partition(A,low,high);//和归并排序的区别在于,快排是先划分再递归,但是划分的过程中就已经包含了排序,而归并算法是直接使用 mid=(low+high)/2 的方式进行划分,所以并不需要调用,此处的 partition 等同于前面归并算法中的 mid=(low+high)/2 和merge(A,low,mid,high);的混合体 QuickSort(A,low,pivot); QuickSort(A,pivot+1,high); }}
- 1
【重写时发生了两个错误导致栈溢出】力扣题解(正常快排)
class Solution {public://int partition(vector<int>& nums,int low,int high){ //int pivot=low;//这种写法是错的,后面low所指向的元素很快会被取代 int pivot=nums[low]; while(low<high){ while(low<high&&nums[high]>=pivot) high--;//此处的low<high漏写,用于防止high还没到外循环的判断条件时就已经不满足low<high,从而产生错误‘ nums[low]=nums[high]; while(low<high&&nums[low]<pivot) low++; nums[high]=nums[low]; } nums[low]=pivot; return low;}//void QuickSort(vector<int>& nums,int low,int high){ if(low<high){//此处的low<high漏写//第二次出错,这里的if错写成了while //当 low=high 时就退出循环 int pivot=partition(nums,low,high); QuickSort(nums,low,pivot);//注意区分这里的low和分治第一题中的0,分治中的0是因为用了substr,导致每个字字符串的low都等于0 QuickSort(nums,pivot+1,high); }}// vector<int> sortArray(vector<int>& nums) { QuickSort(nums,0,(int)nums.size()-1); return nums; }};
- 1
随机选取枢纽的快排
class Solution { int partition(vector<int>& nums, int l, int r) { int pivot = nums[r]; int i = l - 1; for (int j = l; j <= r - 1; ++j) { if (nums[j] <= pivot) { i = i + 1; swap(nums[i], nums[j]); } } swap(nums[i + 1], nums[r]); return i + 1; } int randomized_partition(vector<int>& nums, int l, int r) { int i = rand() % (r - l + 1) + l; // 随机选一个作为我们的主元 swap(nums[r], nums[i]); return partition(nums, l, r); } void randomized_quicksort(vector<int>& nums, int l, int r) { if (l < r) { int pos = randomized_partition(nums, l, r); randomized_quicksort(nums, l, pos - 1); randomized_quicksort(nums, pos + 1, r); } } public: vector<int> sortArray(vector<int>& nums) { srand((unsigned)time(NULL)); randomized_quicksort(nums, 0, (int)nums.size() - 1); return nums; }};
- 1
快速排序的非递归实现
void QuickSortNotR(int* array,int left,int right){ assert(array); stack<int> s; s.push(left); s.push(right);//后入的right,所以要先拿right while(!s.empty)//栈不为空 { int right = s.top(); s.pop(); int left = s.top(); s.pop(); int index = PartSort(array,left,right); if((index - 1) > left)//左子序列 { s.push(left); s.push(index - 1); } if((index + 1) < right)//右子序列 { s.push(index + 1); s.push(right); } }}————————————————版权声明:本文为CSDN博主「清枫若待佳人醉」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。原文链接:https://blog.csdn.net/qq_36528114/article/details/78667034
- 1
7、堆排序(属于选择排序的一种)


相关知识:
大根堆:完全二叉树中,根≥左、右
小根堆:完全二叉树中,根≤左、右
排序步骤(这个程序存在一些错误,正确版参考最后)
1、【2 for 】建立大根堆
一个 for 用来控制往上检查每一个非终端节点
另一个 for 用来保证更换后根节点和孩子节点之后不会导致下面的节点再次违反这个关系,所以用于控制往下检查每个非终端节点

void BuildMaxHeap(vector<int>& nums,int n){//建立大根堆 int k; for(k=n/2;k>=0;k--){//往上依次检查 HeadAdject(nums,k,n); }}void HeadAdject(vector<int>& nums,int k,int n){//k特指我们需要检查的根节点 int i; int temp=nums[k]; for(i=2*k;i<n;i*=2){ if(nums[i+1]>nums[i] && i+1<n) //易错点,保证i+1也有小于n i++; if(temp>=nums[i])//为了保证排序是稳定的,因此要加上等号 break; else{ nums[k]=nums[i]; k=i;//一旦更换了位置后,就要再一一向下验证大根堆的正确性 //nums[i]=temp; 一开始这个写错位置了,如果要写在这个位置,那么上面第二个 if(nums[k]>=nums[i]) 应改为if(nums[k]>=nums[i]) } } nums[k]=temp;//一开始写错了,写成nums[i]=temp;}
- 1
void HeapSort(vector<int>& nums,int n){ BuildMaxHeap(nums,n);//1 for(int i=n-1;i>=0;i--){//2 and 3 swap(nums[0],nums[i]); HeadAdject(nums,0,i-1);//错误:此处一开始写的是n,没注意到在swap之后,移动到最后的元素就不能让再动了 }}
- 1
2、将序列的第一个和最后一个元素交换,也就是将堆顶结点的值交换到堆底,因为堆顶元素一定是所有元素中最大的,所以我们就把堆顶元素以后最后面以后就不要去动他了,用一个for去限定这个范围,之后将换到堆顶的去的未排序序列末尾元素进行不停的下坠
3、重复2过程进行排序
最终力扣通过的代码版本
共有两个错误点:
1、由于数组序号是从0开始的,所以父节点和子节点的计算公式出错(正确的应为 )
d
a
d
=
(
s
o
n
−
1
)
/
2
dad = (son-1)/2
dad=(son−1)/2
s o n = d a d ∗ 2 + 1 son = dad*2+1 son=dad∗2+1
2、由于 上面程序中的 HeadSort 和 BuildMaxHeap 两个函数调用 HeadAdject和这个函数是对于 end 这个参数的定义不同导致

正确的排序版本
class Solution {public: void HeadAdject(vector<int>& nums,int k,int end){ int dad = k; int son = dad * 2 + 1;//这个for第一次调用是正常的调整根节点和孩子节点的位置,第二、三......次调用就是为了验证第一次调用是是否使得下面不满足大根堆的要求 for(;son<=end;) { if (son + 1 <= end && nums[son] < nums[son + 1]) //比较左右孩子 son++; if (nums[dad] > nums[son]) break;//也可以是return else { swap(nums[dad], nums[son]);//发生了swap,则需要对于更换后的孩子节点进行大根堆验证 dad = son; son = dad * 2 + 1; } }} //写程序先写主函数,这个函数是思路 void HeapSort(vector<int>& nums,int n){ for(int k=n/2-1/2;k>=0;k--){//建立大根堆,从最后一个根节点往上依次进行 HeapAdject HeadAdject(nums,k,n-1); } for(int i=n-1;i>=1;i--){ swap(nums[0],nums[i]); //移动完最大的节点后,重新建立大根堆 HeadAdject(nums,0,i-1);//i-1为易错点,因为swap之后,最后一个元素就不能再动了 }} vector<int> sortArray(vector<int>& nums) { int n=(int)nums.size(); HeapSort(nums,n); return nums; }};
- 1
第二次写堆排序(有一些小错误)注释中已经标明
class Solution {public: void HeapAdject(vector<int>& nums,int dad,int end){ for(int son=2*dad+1;dad<=end && son<=end;){//dad<=end冗余 if(nums[son]<nums[son+1] && son+1<=end){ swap(nums[son],nums[son+1]);//错误,不是swap,而是son++ } if(nums[dad]<nums[son]&&son<=end){ swap(nums[dad],nums[son]); } else break; dad=son; son=2*dad+1; }}void HeapSort(vector<int>& nums,int end){ for(int dad=end/2;dad>=0;dad--){ HeapAdject(nums,dad,end); } for(int i=end;i>=1;i--){// swap(nums[0],nums[i]); HeapAdject(nums,0,i-1);// }} vector<int> sortArray(vector<int>& nums) { int n=(int)nums.size(); HeapSort(nums,n-1); return nums; }};
- 1
第二次写的可以运行的版本
class Solution {public: void HeapAdject(vector<int>& nums,int k,int end){ int dad = k; int son = dad * 2 + 1; for(;son<=end;){ //if(nums[son] < nums[son+1] && son+1 <= end) if(son+1 <= end && nums[son] < nums[son+1]) son++; if(nums[dad] > nums[son]) break; else{ swap(nums[dad],nums[son]); dad=son; son=2*dad+1; } }}void HeapSort(vector<int>& nums,int n){ int end=n-1; for(int dad=end/2;dad>=0;dad--){ HeapAdject(nums,dad,end); } for(int i=end;i>=1;i--){// swap(nums[0],nums[i]); HeapAdject(nums,0,i-1);// }} vector<int> sortArray(vector<int>& nums) { int n=(int)nums.size(); HeapSort(nums,n); return nums; }};
- 1
8、桶排序
步骤
1、分类计数
2、依次输出,注意输出数字的次数
- 1
9、计数排序
自己写的(缺少对负数序列的处理能力,因为下标没有负数)
class Solution {private:void SelectionSort(vector<int>& nums){ int max=nums[0];//桶的最大下标为max int n=(int)nums.size(); for(int j=1;j<n;j++){//计算该序列中的最大值确定桶的大小 if(nums[j]>max){ max=nums[j]; } } vector<int> T(max+1,0);//创建大小为max长度的桶 for(int i=0;i<n;i++){//将序列存入桶中 T[nums[i]]++; }int k=0; for(int a=0;a<=max;a++){ while(T[a]>0){ nums[k++]=a; T[a]--; } }}public: vector<int> sortArray(vector<int>& nums) { SelectionSort(nums); return nums; }};
- 1
自己写的正确的版本
class Solution {public: vector<int> sortArray(vector<int>& nums) { int n=(int)nums.size(); int max=INT_MIN; int min=INT_MAX; for(int i=0;i<n;i++){ if(nums[i]>max) max=nums[i]; if(nums[i]<min) min=nums[i]; } int distance=max-min; vector<int> T(distance+1,0);//创建容器 for(int i=0;i<n;i++){//放入容器 T[nums[i]-min]++; } int a=0; for(int i=0;i<distance+1;i++){ while(T[i]>0){ nums[a++]=i+min; T[i]--; } } return nums; }};
- 1
别人写的
class Solution{public: vector<int> sortArray(vector<int>& nums) { int n=nums.size(); if(n<=1)return nums; //比如 要在一个数组中找出最大值,那么可以先定义一个最小值max=INT_MIN int min=INT_MAX,max=INT_MIN; for(int i=0;i<n;++i)//获取该数组中的最大最小值 { if(nums[i]>max)max=nums[i]; if(nums[i]<min)min=nums[i]; } int k=max-min+1;//计数数组长度,其实就是最大最小值之间的距离//这个k和min是用来节约数组长度的,节省了min这么长的空间,还有就是可以处理负数,节约长度是次要的作用 vector<int> count(k,0);//创建一个长度为k的初始值为0的容器 for(int i=0;i<n;++i)//将序列中的元素依据距离最小值的距离依次放入容器 { count[nums[i]-min]+=1; } int loc=0; for(int i=0;i<k;++i)//将容器中记录的nums的值依次按顺序输出给nums { while(count[i]>0) { nums[loc++]=i+min;//重新加上min恢复到原来的元素大小 count[i]-=1; } } return nums; }};
- 1
二、用空间换时间
1、计数排序
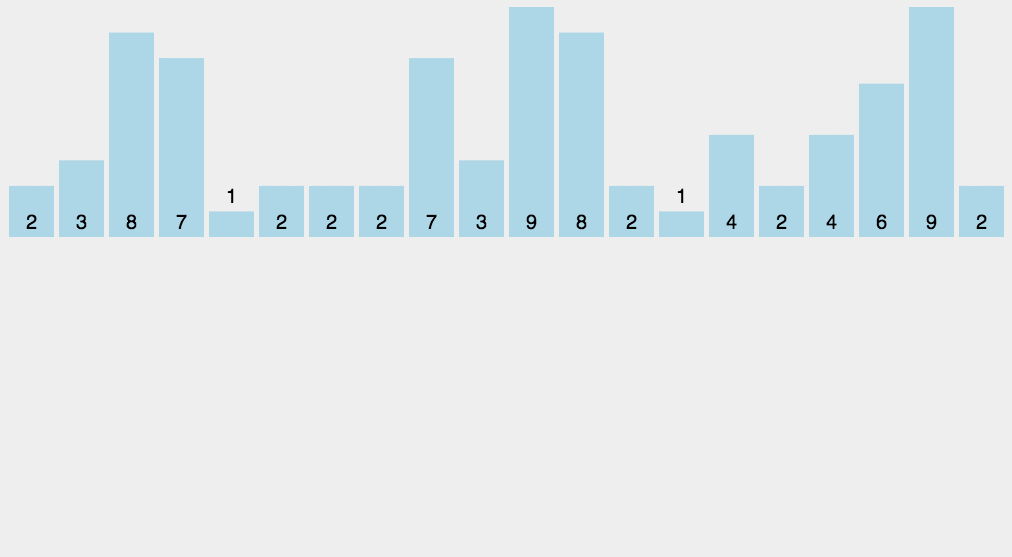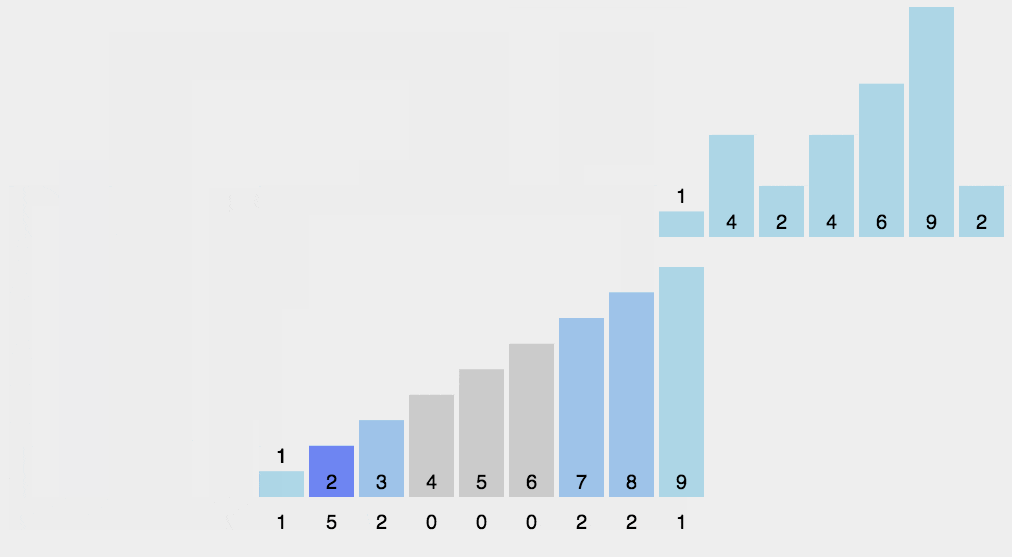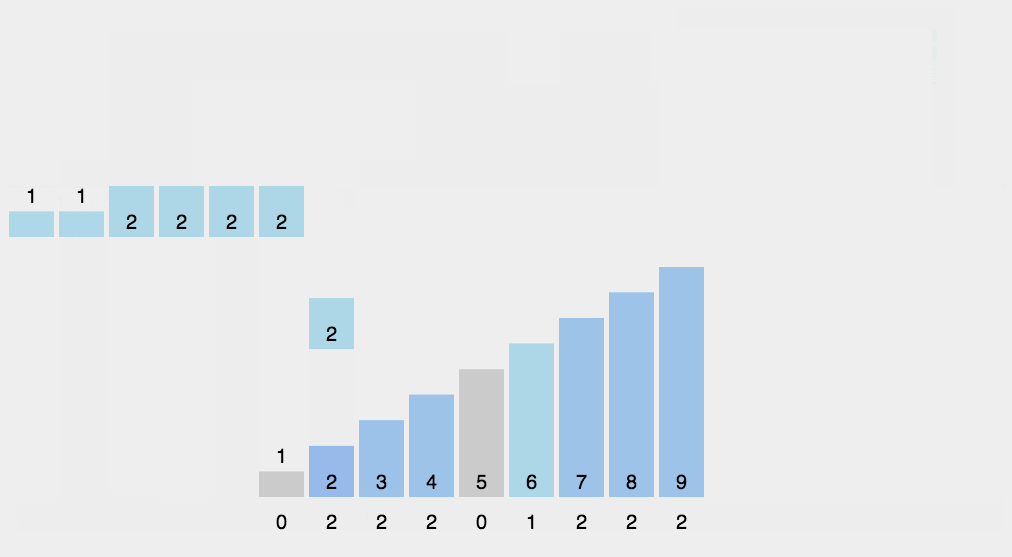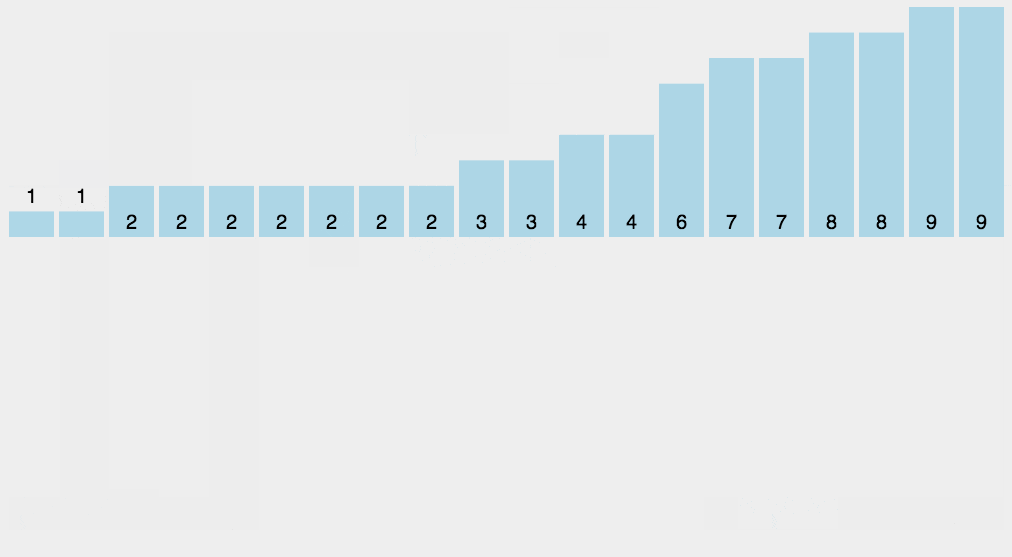
按照类型去刷题
两种类型
- 数据结构
- 算法
从easy开始做










