- 1基于SVD矩阵分解的用户商品推荐(python实现)_基于svd的推荐算法python代码
- 2搭建本地大模型,最简单的方法!效果直逼GPT_ollama下载
- 3树莓派学习(二)笔记本连接_树莓派网线连接上笔记本有什么反应
- 4StableDiffusion对图片进行高清、优化、放大_stablediffusion分辨率怎么调
- 5Android中的消息异步处理机制及实现方案
- 6使用libxml2对xml进行SAX读取_libxml2 sax
- 7Linux安装Python并部署Flask程序_linux flask python
- 8【MySQL】数据类型——MySQL的数据类型分类、数值类型、小数类型、字符串类型_mysql数值型
- 9基于web租车汽车租赁系统设计与实现_汽车租赁系统web
- 10【博学谷学习记录】超强总结,用心分享| hadoop上传和下载文件过程_如何上传文件到hadoop
堆的概念,堆的创建和时间复杂度证明,堆排序,TopK问题。_堆的建立时间复杂度
赞
踩
前言:
博主收集的资料,连载中。
转载请标明出处:New Young
本文介绍 堆—-一种特殊的完全二叉树.
堆
堆的概念
如果完全二叉树中,所有的
父亲结点的值都比其左右孩子结点的值大或者小,这种完全二叉树称为堆,
- 其中将父亲结点大于孩子结点的称为大堆.
- 父亲结点小于孩子结点的称为小堆.
堆的特点
- 堆是一种
特殊的完全二叉树- 根结点的值是最值.
- 堆中某个节点的值总是不大于或不小于其父节点的值 ,即大的值或者小的值总是沉到更下层.
堆的存储
堆是一种
完全二叉树,为了避免不必要的空间浪费,一般用==顺序存储(数组)==的形式来存储数据.typedef int HPDataType; typedef struct Heap { HPDataType* _a; int _size; int _capacity; }Heap;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
堆的功能实现
- 堆的很多功能(堆的创建,堆排序,TopK问题等)都需要向上或者向下调整算法,因此先介绍这2个,再介绍其它功能。
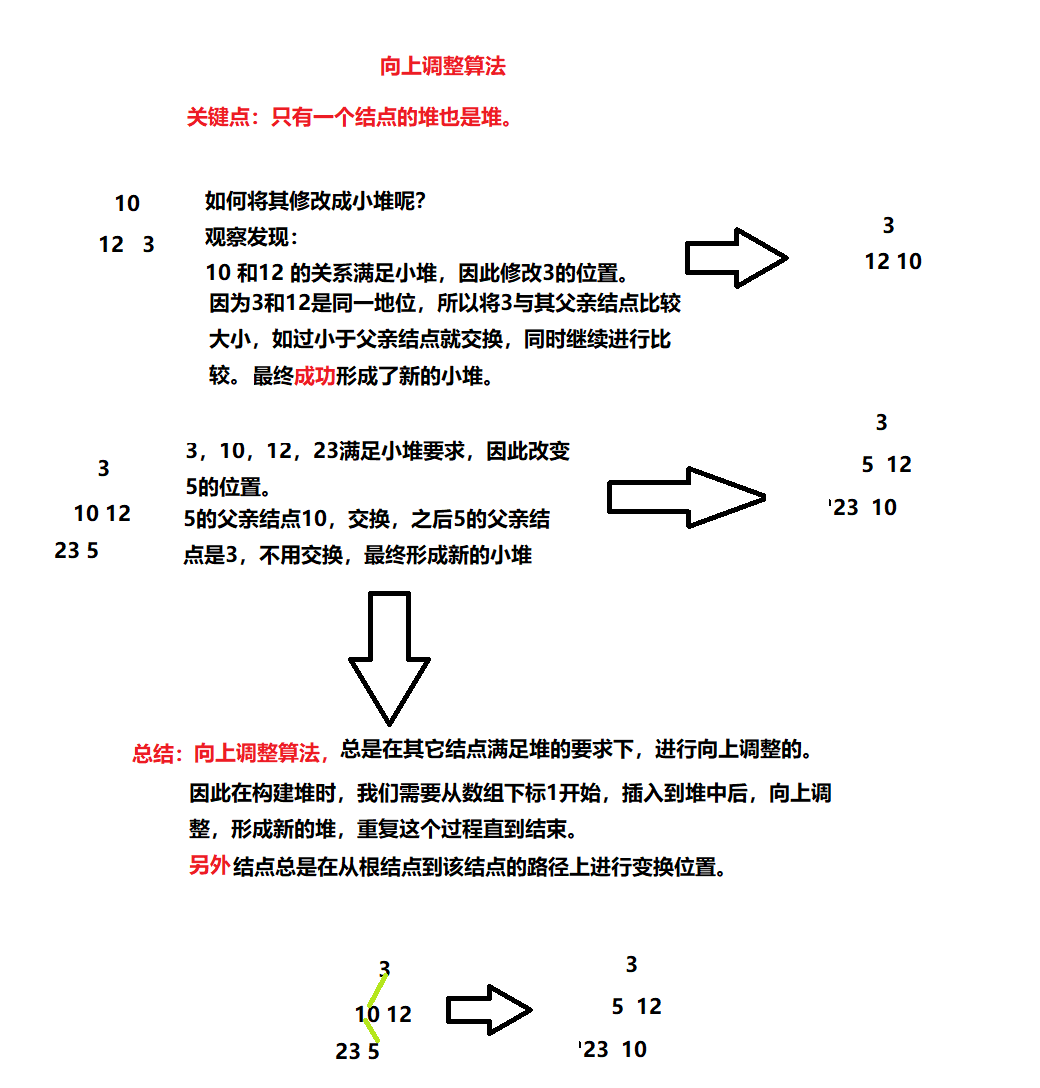
向上调整算法
//向上调整。 void Adjustup(HPDataType* a, int child) { assert(a); int parent = (child - 1) / 2;//无论左右孩子,都可以. while (child>0) { if (a[child] < a[parent]) { Swap(&a[child], &a[parent]); child = parent; parent = (child - 1) / 2; } else { break; } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
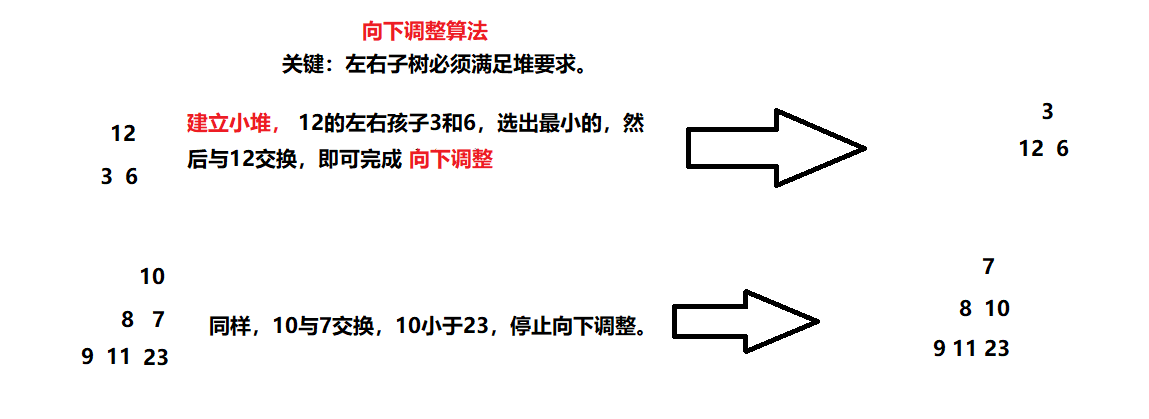
向下调整算法
- 从根结点向下调整前,
左右子树必须满足堆要求—-堆中某个节点的值总是不大于或不小于其父节点的值。
//向下调整 void Adjustdown(HPDataType* a, int n, int parent) { assert(a); int child = 2 * parent + 1; while (child < n)//完全二叉树的特点,当无左子树时,代表达到领界或者越界。 { if ( child+1<n && (a[child+1] < a[child])) { child ++; } if (a[child] < a[parent]) { Swap(&a[child], &a[parent]); parent = child; child = 2 * parent + 1; } else { break; } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
向上与向下调整的比较
| 算法 | 特点 | 使用的范围 | 联系 |
|---|---|---|---|
| 向上调整 | 从堆的尾开始的调整,结点总是在从根结点到该结点的路径上移动 | 堆的插入(Push),堆的创建(Create), | 二者没然的联系,主要看我们的使用角度 |
| 向下调整 | 从堆的头开始的调整,调整前,根结点的左右子树必须满足堆的要求。 | 堆的删除(Pop),堆的创建(Create),TopK问题,堆排序 | |
堆的插入
堆的插入从
尾部进行插入。// 堆的插入 void HeapPush(Heap* hp, HPDataType x) { assert(hp); HeapIsExpandCapacity(hp); hp->_a[hp->_size++] = x; //因为插入元素前,仍是一个堆,只需要要向上调整,就可以让插入的元素走到正确的位置 Adjustup(hp->_a,hp->_size-1); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
堆的删除
堆的删除方式很特殊:
先将根结点与尾结点进行交换,之后从根结点进行向下调整,直到尾结点前
/ 堆的删除,堆的删除删的是跟结点 void HeapPop(Heap* hp) { assert(hp); Swap(&hp->_a[0], &hp->_a[hp->_size - 1]); --hp->_size; Adjustdown(hp->_a, hp->_size, 0); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
堆的扩容
//是否扩容 void HeapIsExpandCapacity(Heap* hp) { if (hp->_size == hp->_capacity) { hp->_capacity = hp->_capacity == 0 ? 4 : 2 * (hp->_capacity); HPDataType* tmp = (HPDataType*)realloc(hp->_a, sizeof(HPDataType)*hp->_capacity); if (tmp == NULL) { printf("Expand Is Failure\n"); exit(-1); } hp->_a = tmp; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
堆的创建
堆的创建有2种主要形式:
- 通过向上调整的算法,–直接在给定数组上进行建队,
- 通过向下调整的算法,通过给定数组的数据,动态规划,重新建立堆。
非原数组,动态建立
效果图
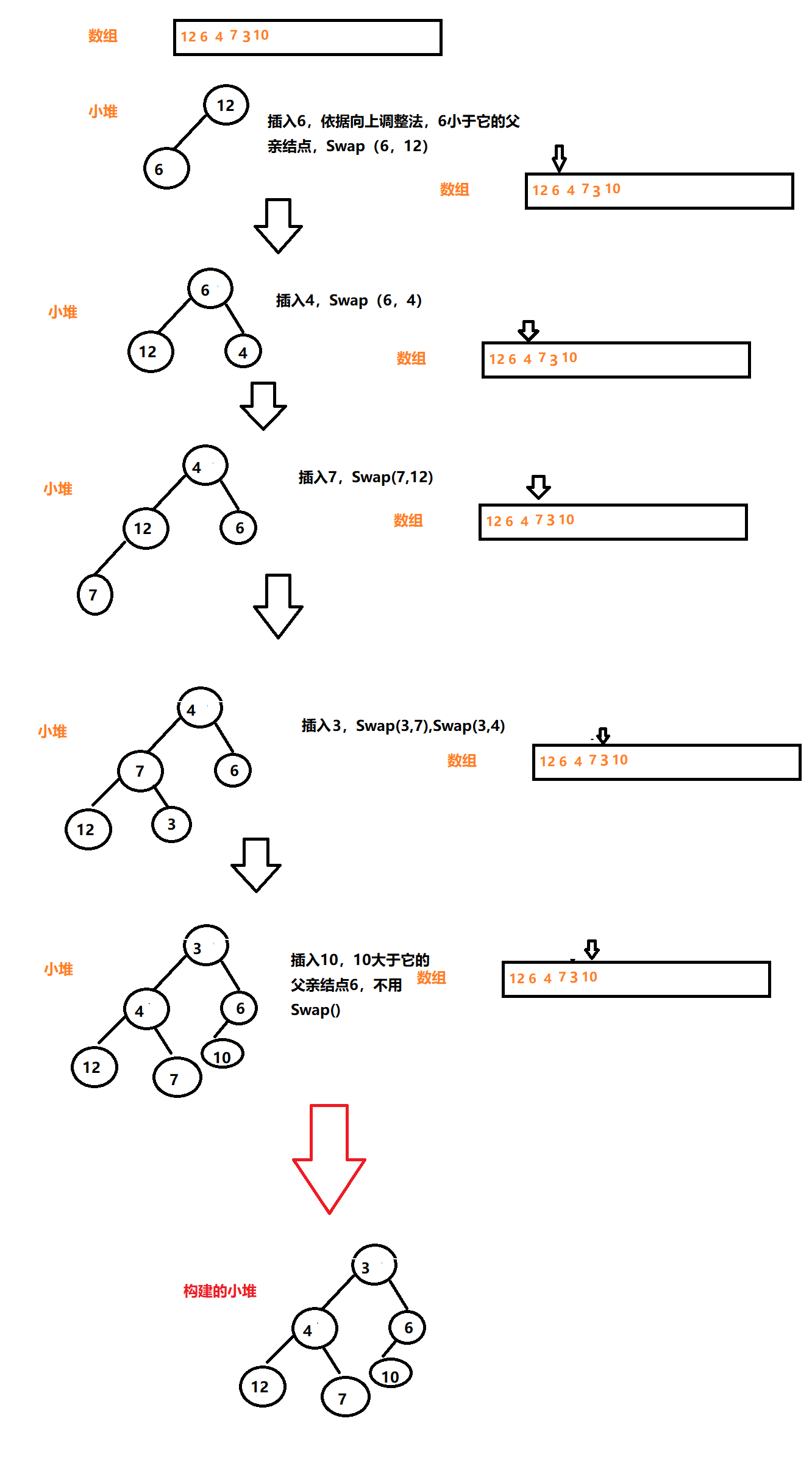
代码
void HeapCreate(Heap* hp, HPDataType* a, int n)
{
assert(hp);
//方式一:不直接在数组上操作,重新构建一个堆
for (int i = 0; i < n; ++i)
{
HeapPush(hp, a[i]);
}
printf("向上调整结果\n");
HeapPrint(hp->_a, hp->_size);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
原数组
向上调整法:
- 只有一个结点的堆也堆,因此我们从下标1开始插入堆,然后向上调整,重复这个过程直到建堆完成。
代码
void HeapCreate(Heap* hp, HPDataType* a, int n)
{
assert(hp);
思路:只有一个结点也是堆,通过插入,向上调整,建堆。
for (int i = 1; i < n; ++i)
{
Adjustup(a, i);
}
HeapPrint(a, n);
}向下调整法
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
向下循环法
因为堆是一种递归结构,这表明如果我们再向下调整整个堆前,可以先调整它的左右子树,通过这种递归,最终我们需要从非叶结点的父亲结点回推
效果展示
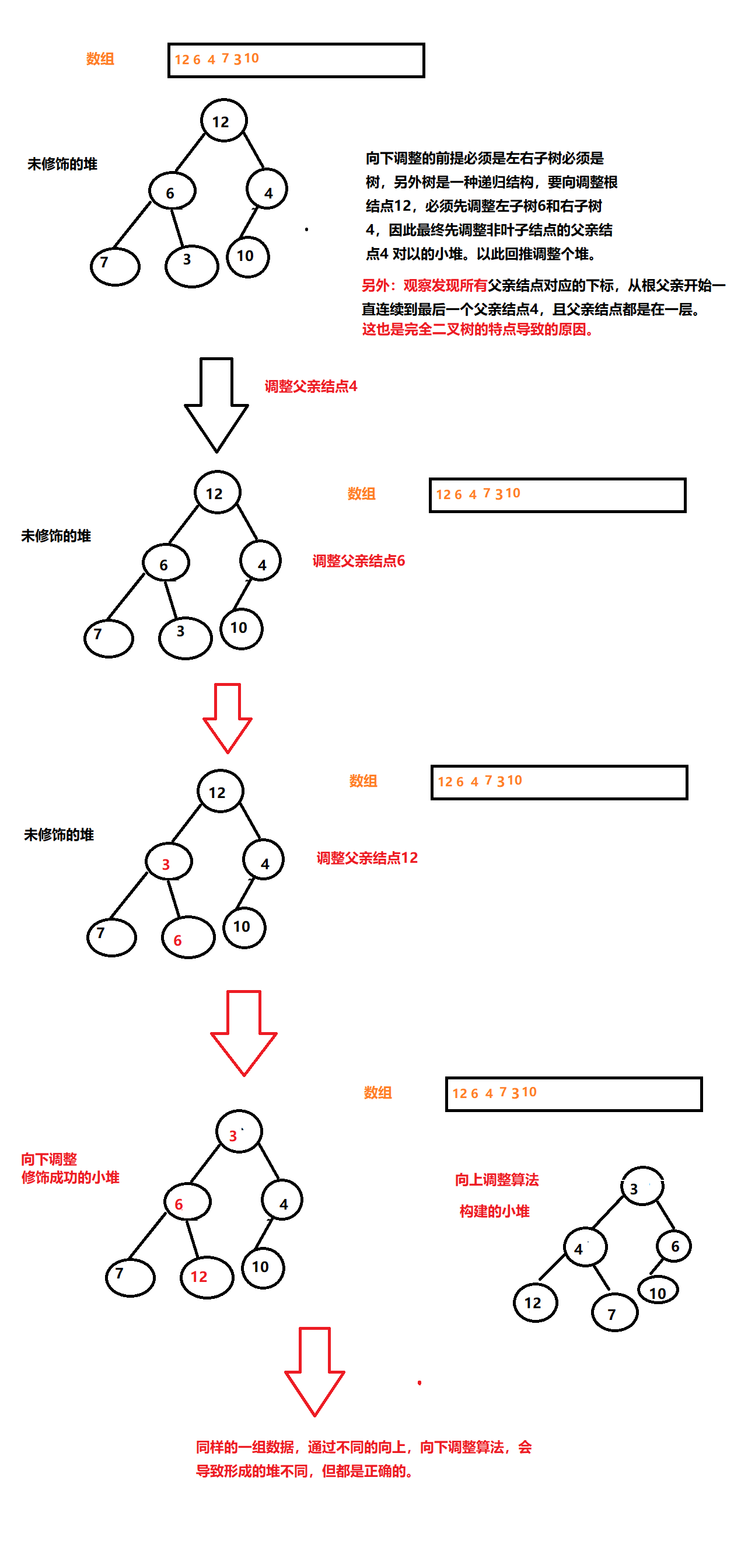

代码
//思路:只有一个结点也是堆,通过插入,向下调整,建堆。
void HeapCreate(Heap* hp, HPDataType* a, int n)
{
assert(hp);
for (int parent = (n - 1 - 1) / 2; parent >= 0; --parent)
{
Adjustdown(a, n, parent);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
递归法
代码
void RecDown(HPDataType* a, int n, int parent) { assert(a); int child = 2 * parent + 1; if (child >= n ) { Adjustdown(a, n, parent-1); return; } else { RecDown(a, n, parent + 1); Adjustdown(a, n, parent); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
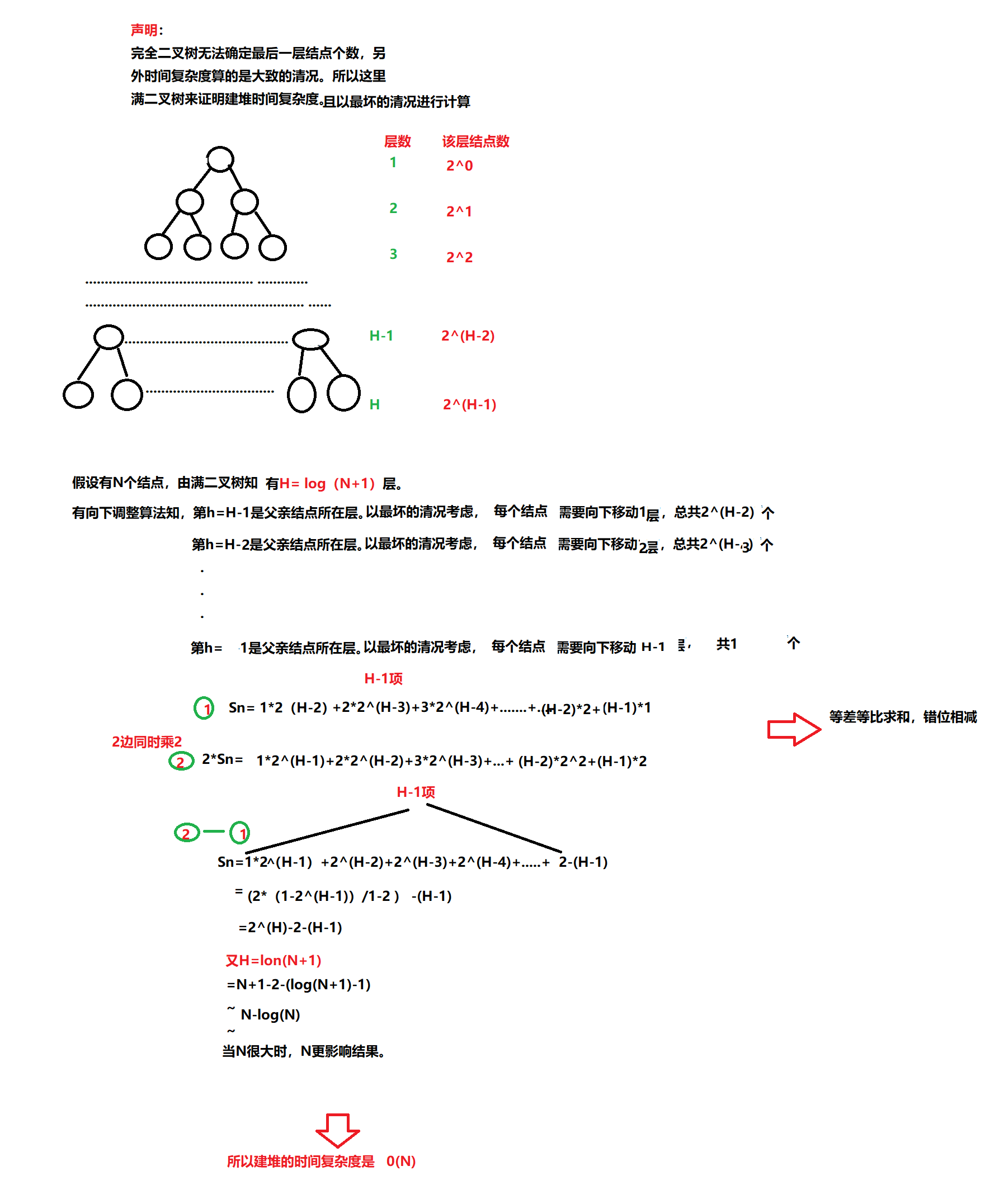
建堆的创建时间复杂度证明
堆排序
思路
我们再删除堆操作中,先将头尾交换,之后对头向下调整。再结合堆的根结点是
最值.如果我们每次都将堆的根结点与尾交换,然后将尾前面就行向下调整,这样就可以完成排序。如果想
降序,因为最大值在最后,所以要求第一个根结点是最大值,这就要求我们建大堆,让根结点成为最大值。反之,升序,建小堆。
效果
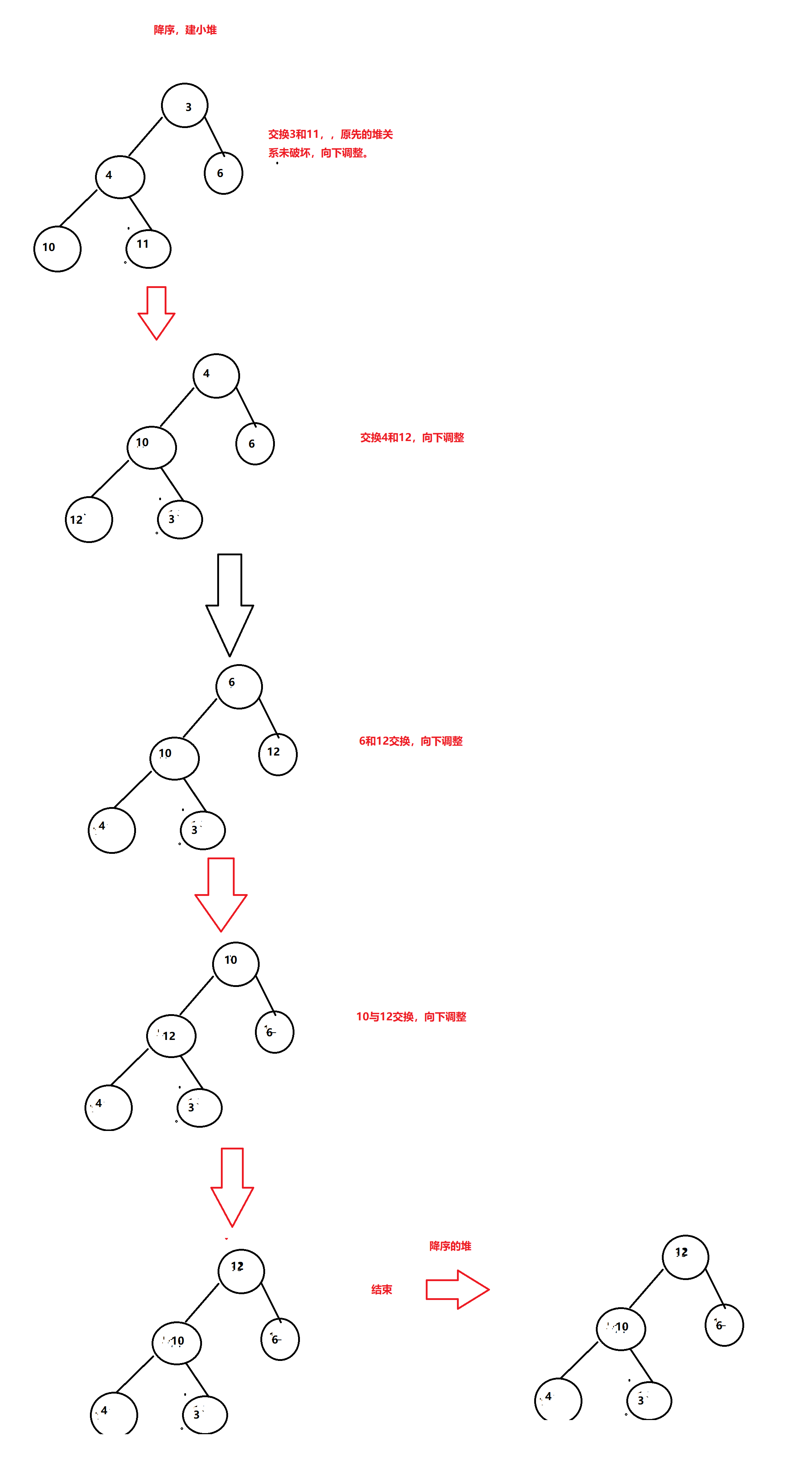

代码
// 降序,建小堆,跟结点必然是最小结点, //所以首尾交换后,跟的左右子树仍是关系未破坏的堆, //所以可以通过向下调整的方式,再次选出最小的结点, //重复改过程。 void HeapSort(HPDataType* a, int n) { assert(a); //建堆 // // // //方式一:向上调整算法 //for (int i = 1; i < n; ++i) //{ // Adjustup(a, i); //} //HeapPrint(a, n); //方式二,非递归向下调整算法。 //方式二:在数组上操作 //思路:只有一个结点也是堆,通过插入,向下调整,建堆。 //for (int parent = (n - 1 - 1) / 2; parent >= 0; --parent) //{ // Adjustdown(a, n, parent); //} //printf("向下调整结果\n"); //HeapPrint(a, n); 方式三,递归向下调整算法建堆 // //递归法建堆 printf("递归向下调整结果\n"); RecDown(a, n, 0); for (int i = 0; i < n-1; ++i) { Swap(&a[0], &a[n -1- i ]); Adjustdown(a, n-1-i, 0); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
TopK问题
思路:
问题:如果有10亿个数,找出其中最大的前10。
首先10亿个数,只能将他们先存到文件中,之后取和适数量放到内存中。
这里为了方便,假设文件存放了N(我实际假设环境是100个数)个数,一次取t个数存入内存,需要K次。
如果我们用排序的思想—-这里用选择法,时间复杂度为:0(K*N^2)
发现很大,效率不高。
我们观察
堆,发现,堆的根结点是最值,根以下的结`点`都大于或者小于根结点,如果我们将除了==建堆以外==的数据与==根结点==比较,如果大于根结点,就替换根结点,同时进行向下调整,这样的话大数就沉到下面了,而最小的,次小等等都会因为根结点而被替换调。如果要找最大的前K个,那么必须建小堆,如果建大堆,如果根结点恰好是最大的一个,这就会Creash。但是建小堆就不用担心,根结点是最小的,不会Creash。
文件存储数据代码
效果
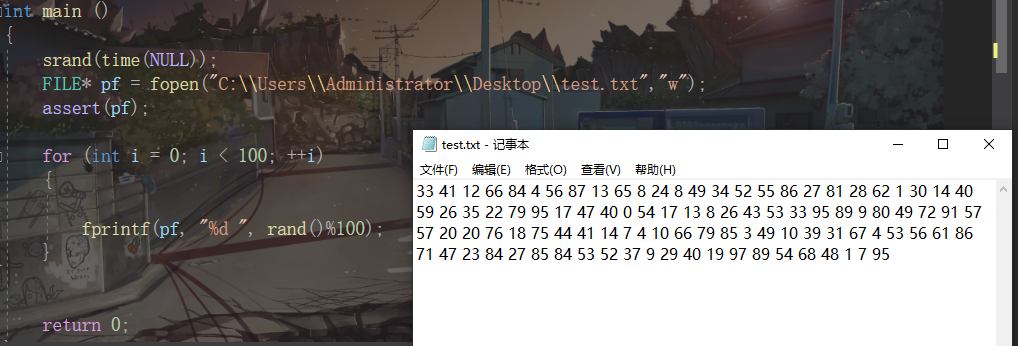
int main ()
{
srand(time(NULL));
FILE* pf = fopen("C:\\Users\\Administrator\\Desktop\\test.txt","w");
assert(pf);
for (int i = 0; i < 100; ++i)
{
fprintf(pf, "%d ", rand()%100);
}
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
TopK代码
效果
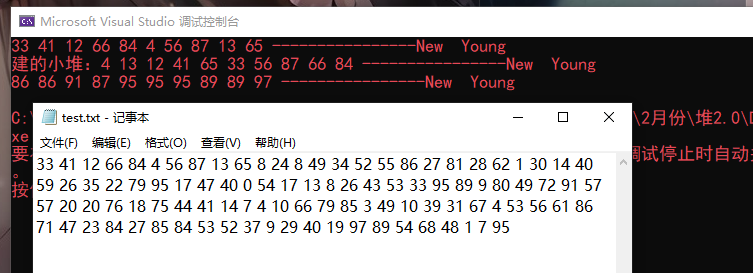
代码
//找最大的 k个,则建立小堆,因为大堆可能会导致最大的丢失。 //先去文件中的前N个放到数组中,建成小堆,之后继续将数据重新放到数组中,然后依次比较堆根结点。直到EOF。 void TopK( int n, int k) { FILE* pf = fopen("C:\\Users\\Administrator\\Desktop\\test.txt", "r"); assert(pf); Heap hp; HeapInit(&hp); int* a = (int*)calloc(k ,sizeof(int)); assert(a); //建小堆 for (int i = 0; i < k; ++i) { if (feof(pf)) { break; } else { fscanf(pf, "%d ", &a[i]); } } HeapPrint(a, k); //这里不能在原数组上建堆。动态建堆 HeapCreate(&hp, a, k); printf("建的小堆:"); HeapPrint(hp._a, hp._size); while (!feof(pf)) { int i = 0; for ( i = 0; i < k; ++i) { if (feof(pf)) { break; } else { fscanf(pf, "%d ", &a[i]); } } for (int j = 0; j < i; ++j) { if (a[j] > HeapTop(&hp)) { hp._a[0] = a[j]; Adjustdown(hp._a, k, 0); } } } HeapPrint(hp._a, hp._size); HeapDestory(&hp); free(a); a = NULL; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69