算法分析与设计——算法分析基础_多个因素影响时间 用什么算法

一、实验目的

1.了解影响程序运行时间的主要因素；
2.掌握渐近时间复杂度的表示方法；
3.掌握递归关系的时间复杂度计算。

二、实验原理

• 影响程序运行时间的主要因素
  （1）程序所依赖的算法；
  （2）问题规模和输入数据；
  （3）计算机系统性能。
• 渐近时间复杂度的表示
  （1）大 O 记号
  设函数 f(n)和 g(n)是定义在非负整数集合上的正函数，如果存在两个正常数 c 和 n0，使得当 n≥n0 时，有 f(n)≤cg(n)，则记做 f(n) = O(g(n))，称为大 O 记号（big Oh notation）。
  （2）Ω记号
  设有函数 f(n)和 g(n)是定义在非负整数集合上的正函数，如果存在两个正常数 c 和 n0，使得当 n≥n0 时，有 f(n)≥c g(n)，则记做 f(n) =Ω(g(n))，称为Ω记号（omega notation）。
  （3）Θ记号
  设有函数 f(n)和 g(n)是定义在非负整数集合上的正函数，如果存在正常数 c1，c2 和 n0，使得当 n≥n0 时，有 c1 g(n)≤f(n)≤c2 g(n)，则记做 f(n) =Θ(g(n))，称为Θ记号（Theta notation）。
• 递归关系的时间复杂度计算方法
  （1）基本迭代法；
  （2）换元法；
  （3）递归树；
  （4）主定理法。

三、实验内容

1. 设a,b,c是3个塔座。开始时，在塔座a上有一叠共n个圆盘，这些圆盘自下而上，由大到小地叠在一起。各圆盘从小到大编号为1,2,…,n,现要求将塔座a上的这一叠圆盘移到塔座c上，并仍按同样顺序叠置。
   提示:

原理：

• hanoi 函数的第 1 个参数是柱子上需要移动的圆盘的个数，后三个参数分别为三根柱子的标识。首先当 n 为 1 时，需要移动的圆盘只有一个，直接把 A 上的圆盘移动到 C 上就可以了，同时代码结束，因为已经没有需要移动的圆盘了。
• 接下来是汉诺塔实现的关键，即把 A 上所有的圆盘移动到 C 上，需要先把 A 最上面的 n-1 个圆盘移动到 B 上，于是有了“hanoi(n-1,A,C,B);”这样一行递归调用，接下来只需要把 A 上最后剩下的最大的圆盘移动到 C 上。
• 现在 B 上有 n-1 个圆盘，C 上有一个最大的圆盘，接下来把 B 上这 n-1 个圆盘也移动到 C 上。此时把 B 想象成之前的 A，有一堆待移动的圆盘；把 A 想象成之前的 B，是空的柱子，这时我们只需要把调用方式变为“hanoi(n-1,B,A,C);”，就可以完成移动，这就是递归调用的思想所在了。

程序：

#include <iostream>
using namespace std;

void hanoi(int n,int p1,int p2,int p3)
//p1，p2，p3表示利用2号将1号的n个珠子移动到3号
{
	if(1==n)
		cout<<"盘子从"<<p1<<"移到"<<p3<<endl;
    //递归函数退出点，当珠子数量为1时，直接移动，结束
	else
	{
		hanoi(n-1,p1,p3,p2);
		//第一步p1，p3，p2表示利用3号将1号的n-1个珠子移动到2号
		cout<<"盘子从"<<p1<<"移到"<<p3<<endl;
		//第二步将剩余的一个珠子从1移到3
		hanoi(n-1,p2,p1,p3);
		//第三步p2，p1，p3表示利用1号将2号的n-1个珠子移动到3号
	}
}

int main()
{
    cout<<"姓名：张俊   学号：201802524  ：\n";
    int a,p1=1,p2=2,p3=3;
    //定义移动的珠子数a，以及三个杆子
    cout<<"请输入在一号杆上的珠子数：";
    cin>>a;
    //用a接受输入的珠子数
    hanoi(a,p1,p2,p3);
    //调用递归函数，实现a个珠子通过p2从p1移动到p3

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

测试：

时间复杂度：

设盘子个数为n时，需要T（n)步，把A柱子n-1个盘子移到B柱子，需要T（n-1)步，A柱子最后一个盘子移到C柱子一步，B柱子上n-1个盘子移到C柱子上T（n-1)步。
得递推公式T（n）=2T（n-1)+1
所以汉诺塔问题的时间复杂度为O(2^n);

2. 分别利用递归代码和非递归代码计算斐波那契数列；比较效率，分析效率差异可能的产生原因。
   
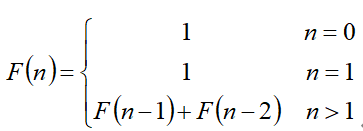
   使用递归实现
   原理：
   给定一个数N时，需要先计算N-1 和N-2的情况，但是在计算N-1时同样要用计算N-2的情况，每个递归调用都触发另外两个递归调用，而这两个调用的任何一个又将调用另外连个递归调用
   程序：

#include <iostream>
using namespace std;

long Fib(int n)
{
    if (n == 0)
        return 0;
    //递归调用出口
    if (n == 1)
        return 1;
    //递归调用出口
    if (n > 1)
        return Fib(n-1) + Fib(n-2);
    //数为前两个数总和
    return 0;
}

int main()
{
    cout<<"姓名：张俊   学号：201802524：\n";
    int month;
    //定义总数month
    cout<<"请输入总数：";
    cin>>month;
    //输入值赋给参数month
    cout<<"经过"<<month<<"次生成后，总总数为："<<Fib(month)+Fib(month-1);
    //调用两次递归函数，参数分别是month和month-1
    //计算总数

    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

测试：
以12为测试：

复杂度：
这样的递归算法虽然只有简单的几行，但是效率却很低。
时间复杂度 ----- O(2^N)
由于使用递归时，其执行步骤是：要得到后一个数之前必须先计算出之前的两个数，即在每个递归调用时都会触发另外两个递归调用，例如：要得到F(10)之前得先得到F(9)、F(8)，那么得到F(9)之前得先得到F(8)、F(7)…如此递归下去

使用非递归实现：
原理：
要想非递归实现斐波拉契函数，只要保存f(n-2)、f(n-1)就可以，将其存入list中。当n=2时，只需要把list中的两个数相加一次即可，同时将相加的数存入list[1],将原来的list[1]存入list[0]中。
程序：

#include <iostream>
using namespace std;

int fibFor(int n);  //声名生成斐波拉契数列的函数
int main() {
	cout << "姓名：张俊   学号：201802524\n";
	int n;
	cout << "n=";
	cin >> n;    //输入总数
	cout << "结果：" << fibFor(n) << endl;  //打印函数调用运行结果

	return 0;
}
int fibFor(int n) {   //定义函数主体
	int a = 1;
	int b = 1;   //初始两个值1，1
	int result;   //最终结果
	if (n <= 1) return 1;   //如果n小于1，直接退出
	else
	{
		for (int i = 1; i < n; i++)
		{
			result = a + b;
			a = b;
			b = result;
		}
		return result;
	}  //否则将前两个数相加赋值给第三个数  并输出
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

测试：

复杂度：
时间复杂度为O(N)，空间复杂度为O(1)
借助两个变量a 和 b ，每次将 a 和 b 相加后赋给 result ，再将 b 赋给 a ，result 赋给 b，如此循环。

比较递归和非递归：
由于使用递归时，其执行步骤是：要得到后一个数之前必须先计算出之前的两个数，即在每个递归调用时都会触发另外两个递归调用，例如：要得到F(10)之前得先得到F(9)、F(8)，那么得到F(9)之前得先得到F(8)、F(7)…如此递归下去

从上图我们可以看出，这样的计算是以 2 的次方在增长的。除此之外，我们也可以看到，F(8)和F(7)的值都被多次计算，如果递归的深度越深，那么F(8)和F(7)的值会被计算更多次，但是这样计算的结果都是一样的，除了其中之一外，其余的都是浪费，可想而知，这样的开销是非常恐怖的！

说明：
代码中一定位置或注释中一定要加入能标记自己身份的信息，如学号、姓名等。
粘贴在Word中的代码最好保留原始着色，一定要清楚，有缩进，有注释。