机器人中欧拉角，偏航角、俯仰角、横滚角的自锁现象与四元数的来源于推导_欧拉角自锁

想要讲欧拉角，我们需要先讲物体的姿态与自由度。

什么是物体的位姿

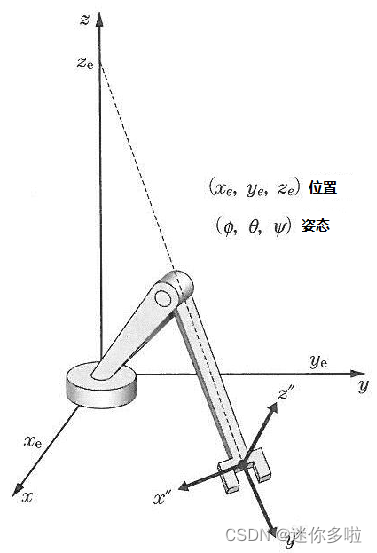
为了描述物体(此处指的是我们的末端执行器)在空间中的位置，我们可以用一个3*1的位置矩阵去描述。
$$P^{\prime \prime }=[P_X^{\prime \prime },P_Y^{\prime \prime },P_Z^{\prime \prime }{]}^T$$
其中P’‘就是末端执行器的自身坐标系（x’‘y’‘z’'）原点在固定坐标系(xyz)下的坐标。

为了描述物体在空间中的姿态，我们可以使用3*3的姿态矩阵去描述。
R ′ ′ = [ n x ′ ′ o x ′ ′ a x ′ ′ n y ′ ′ o y ′ ′ a y ′ ′ n z ′ ′ o z ′ ′ a z ′ ′ ] R''= \left[

$$\begin{matrix} n_x'' &o_x''&a_x'' \\ n_y'' &o_y''&a_y'' \\ n_z''&o_z''&a_z'' \\ \end{matrix}$$ \right] R′′= ​nx′′​ny′′​nz′′​​ox′′​oy′′​oz′′​​ax′′​ay′′​az′′​​ ​
其中三个列向量分别代表了末端执行器自身坐标系的x’‘,y’‘,z’'轴上的单位向量在固定坐标系下的坐标
或者说该矩阵的每个值是自身坐标系坐标轴上的单位向量在固定坐标系下x,y,z的投影。

当然我们也可以使用四元数，一个4*1的矩阵去描述物体的姿态。也可以使用欧拉角来描述物体的姿态。如果你不懂四元数和欧拉角没关系，接下来我会介绍他们。

什么是自由度

自由度在很多领域中都有应用。这里只介绍一下与本文相关的一个概念：自由度是根据机械原理，机构具有确定运动时所必须给定的独立运动参数的数目。
一般来讲在机器人学科中关节的数目就是自由度。
我们都知道一个刚体在空间中的自由度是6，注意此处是刚体（因为会变形的物体可能有更多的自由度）。其中刚体能够沿3个轴做直线运动，有3个自由度；
能够绕3个轴旋转，有3个自由度。共6个自由度。
看起来很显然对吧。
平动的三个自由度是很容易理解的，但是转动的三个自由度就不是那么显然了。
我们从数学概念的自由度入手来理解这件事：
假设我们有三个变量:$x,y,z$
但是有一个限制条件：$x+y+z=18$
此时我们的自由度为：$3(变量)-1（限制）=2（自由取值的变量）$

从姿态矩阵推导旋转自由度为3

我们前文提到：
姿态矩阵是我们描述物体姿态的一个矩阵，其中有9个变量。
R ′ ′ = [ n x ′ ′ o x ′ ′ a x ′ ′ n y ′ ′ o y ′ ′ a y ′ ′ n z ′ ′ o z ′ ′ a z ′ ′ ] R''= \left[

$$\begin{matrix} n_x'' &o_x''&a_x'' \\ n_y'' &o_y''&a_y'' \\ n_z''&o_z''&a_z'' \\ \end{matrix}$$ \right] R′′= ​nx′′​ny′′​nz′′​​ox′′​oy′′​oz′′​​ax′′​ay′′​az′′​​ ​
那我们的限制条件有哪些呢:
每个行向量为单位矩阵（3个限制条件）：
$n_x^{\prime \prime 2}+n_y^{\prime \prime 2}+n_z^{\prime \prime 2}=1$
$o_x^{\prime \prime 2}+o_y^{\prime \prime 2}+o_z^{\prime \prime 2}=1$
$a_x^{\prime \prime 2}+a_y^{\prime \prime 2}+a_z^{\prime \prime 2}=1$
每个行向量之间两两垂直（3个限制条件）：
$(n_x^{\prime \prime }，n_y^{\prime \prime }，n_z^{\prime \prime })\cdot (o_x^{\prime \prime }，o_y^{\prime \prime }，o_z^{\prime \prime })=0$
$(n_x^{\prime \prime }，n_y^{\prime \prime }，n_z^{\prime \prime })\cdot (a_x^{\prime \prime }，a_y^{\prime \prime }，a_z^{\prime \prime })=0$
$(o_x^{\prime \prime }，o_y^{\prime \prime }，o_z^{\prime \prime })\cdot (a_x^{\prime \prime }，a_y^{\prime \prime }，a_z^{\prime \prime })=0$
因此此时的自由度为：$9(变量)-6（限制）=3（自由取值的变量）$

从四元数推导旋转自由度为3

需要推导四元数的可以看我的另一篇文章：

https://blog.csdn.net/weixin_49813139/article/details/126733797

四元数我们一般写成这样
$p=[cos(\theta /2),sin(\theta /2)\mathbf{u}]$
其中$\mathbf{u}$为旋转轴是一个单位向量，$\theta$为绕轴旋转的角度。
将四元数写成完整形式为 $p=[cos(\theta /2),sin(\theta /2){\mathbf{u}}_x,sin(\theta /2){\mathbf{u}}_y,sin(\theta /2){\mathbf{u}}_z]$
该公式中很容易推导的是四元数各分量的平方和为1。
因此我们有变量4个，限制条件1个。
此时的自由度为：$4(变量)-1（限制）=3（自由取值的变量）$

从上文可以看到，我们要描述一个刚体的姿态，我们最小的独立变量个数就是3，因此我们说刚体的转动自由度为3。

什么是欧拉角

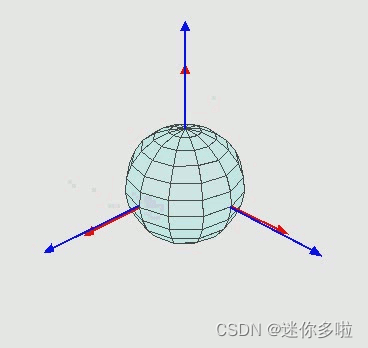
上图是一个很常见的介绍欧拉角的图，摘自维基百科，我们根据右手系的定义(假设竖直向上的为Z轴)可以知道，该图是先绕Z轴（运动坐标系）转，然后绕X轴（运动坐标系）转，最后又绕Z轴（运动坐标系）转形成的最终的坐标系（运动坐标系）。

右手系

右手系可以用手的多种形状去展示，这里用百度百科的图如下：

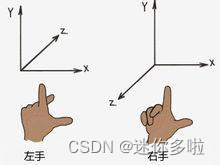
我的老师教我的是右手大拇指是Z轴，然后右手从张开到握起来分别经过了X,Y轴。

按照旋转的轴的顺序，欧拉角一共有12种：
六种：Proper Euler angles (z−x−z, x−y−x, y−z−y, z−y−z, x−z−x, y−x−y）
六种：Tait-Bryan angles (x−y−z, y−z−x, z−x−y, x−z−y, z−y−x, y−x−z）
也就是说我们可以先绕Z轴转，再绕X轴转，再绕Z轴转，也可以先绕X轴转，再绕Y轴转，再绕Z轴转.
下图是按照运动坐标系X-Y-Z分别旋转60°、30°、10°的动图。

按照固定的轴的顺序，欧拉角也有12种。
比如下图是按照固定坐标系X-Y-Z分别旋转60°、30°、10°的动图。

因此欧拉角严格来说有12+12=24种。

欧拉角的多种形式造成了我们在不同学科中使用欧拉角时一定要知道对方学科的欧拉角是用的哪种顺序进行旋转的。
比如：经典力学中使用zxz，量子力学使用的是zyz，航空航天使用zyx/zxy

https://www.zhihu.com/tardis/landing/m/360/art/98320567

本文不讲解欧拉角的证明和矩阵相关内容，这部分很多文章都有。

欧拉角与偏航角、俯仰角、横滚角的关系

偏航角、俯仰角、横滚角是欧拉角24种中的一种。使用欧拉角表示姿态,令ψ,θ和Φ代表ZYX欧拉角,分别称为偏航角、俯仰角和横滚角。也就是说我们先绕Z轴转ψ称为偏航角，再绕Y轴转θ称为俯仰角，再绕X轴转Φ称为横滚角。
这里说的X,Y,Z为运动坐标系的坐标轴。
图中X轴朝前，Z轴朝上，Y轴根据右手系确定朝右。

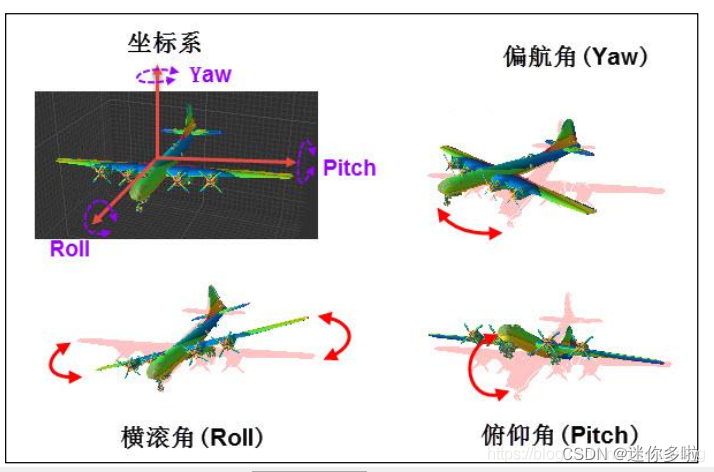
下图是一个动图，可以看到从上到下，进度条分别表示的是绕ZYX轴旋转的角度。我们从上到下进行调整可以发现，我们先后调整的是飞机的偏航角、俯仰角、横滚角。（注意顺序 ，调整的顺序是Z、Y、X。也就是说，你调整好Z、Y、X的角度后再去返回去调整Z，他的含义依旧是先Z后Y后X，与你改变数值的顺序无关（此处也是造成欧拉角死锁的原因））