数据分享|R语言用lme4多层次（混合效应）广义线性模型（GLM），逻辑回归分析教育留级调查数据...

全文链接:http://tecdat.cn/?p=22813

本教程为读者提供了使用频率学派的广义线性模型（GLM）的基本介绍。具体来说，本教程重点介绍逻辑回归在二元结果和计数/比例结果情况下的使用，以及模型评估的方法（点击文末“阅读原文”获取完整代码数据）。

本教程使用教育数据例子进行模型的应用。此外，本教程还简要演示了用R对GLM模型进行的多层次扩展。最后，还讨论了GLM框架中的更多分布和链接函数。

相关视频

本教程包含以下结构。
1. 准备工作。
2. 介绍GLM。
3. 加载教育数据。
4. 数据准备。
5. 二元（伯努利）Logistic回归。
6. 二项式 Logistic 回归。
7. 多层次Logistic回归。
8. 其他族和链接函数。

本教程介绍了：
- 假设检验和统计推断的基本知识。
- 回归的基本知识。
- R语言编码的基本知识。
- 进行绘图和数据处理的基本知识。

广义线性模型（GLM）简介

对于y是连续值得情况，我们可以用这种方式处理，但当y是离散值我们用普通线性模型就不合适了，这时我们引用另外一种模型 --- Generalised Linear Models 广义线性模型。

为了获取GLM模型，我们列出3个条件：

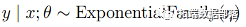1. ，也就是y|x为指数族分布，指数族分布形式：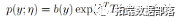

2. 如果我们判断y的假设为 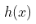，则。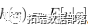

3. 自然参数和输入x呈线性关系：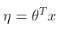

这3个条件的来由我们不讨论，我们只知道做这样的假设是基于“设计”的选择，而非必然。

我们以泊松回归为例, y服从泊松分布 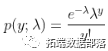，化为指数族形式，我们可以得到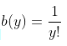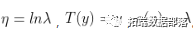。所以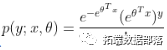

之后即为最大似然法的过程。

教育数据

本教程中使用的数据是教育数据。

该数据来源于全国性的小学教育调查。数据中的每一行都是指一个学生。结果变量留级是一个二分变量，表示一个学生在小学教育期间是否留过级。学校变量表示一个学生所在的学校。个人层面的预测因素包括。  性别（0=女性，1=男性）和学前教育（受过学前教育，0=没有，1=有）。学校层面是学校平均SES（社会经济地位）得分。

本教程利用教育数据试图回答的主要研究问题是。

忽略数据的结构，性别和学前教育对学生是否留级的影响是什么？
忽略数据的结构，学校平均SES对学生留级比例的影响是什么？
考虑到数据的结构，性别、学前教育和学校平均SES对学生是否留级有什么影响？
这三个问题分别用以下这些模型来回答：二元逻辑回归；二项逻辑回归；多层次二元逻辑回归。

数据准备

加载必要的软件包

# 如果你还没有安装这些包，请使用install.packages("package_name")命令。
library(lme4) # 用于多层次模型
library(tidyverse) # 用于数据处理和绘图

导入数据

head(Edu)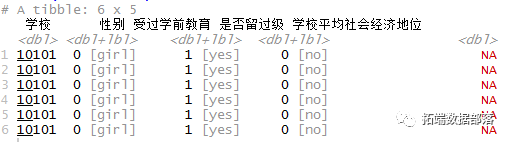

数据处理

mutate(学校 = factor(学校),
         性别 = if_else(性别 == 0, "girl", "boy"),
         性别 = factor(性别, levels = c("girl", "boy")),
         受过学前教育 = if_else(受过学前教育 == 0, "no", "yes"),
         受过学前教育 = factor(受过学前教育, levels = c("no", "yes")))

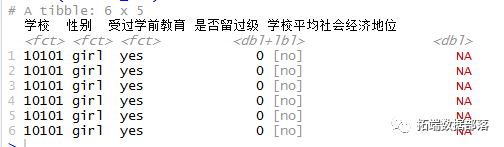
检查缺失的数据

summarise_each((~sum(is.na(.))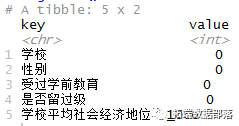

数据中，经济地位变量有1066个观测值缺失。对缺失数据的处理本身就是一个复杂的话题。为了方便起见，我们在本教程中简单地将数据缺失的案例删除。

二元逻辑回归

探索数据：按性别和学前教育分类的留级数量 

group_by(性别) %>%
  summarise(是否留过级 = sum(是否留过级))