2024数维杯（C题）数学建模解题思路|完整代码论文集合|Tina表姐精心制作|天然气水合物问题_数维杯c题

我是Tina表姐，毕业于中国人民大学，对数学建模的热爱让我在这一领域深耕多年。我的建模思路已经帮助了百余位学习者和参赛者在数学建模的道路上取得了显著的进步和成就。现在，我将这份宝贵的经验和知识凝练成一份全面的解题思路与代码论文集合，专为本次赛题设计，旨在帮助您深入理解数学建模的每一个环节。
让我们来分析数维杯C题！

数维杯（C题）完整内容可以在文章末尾领取！

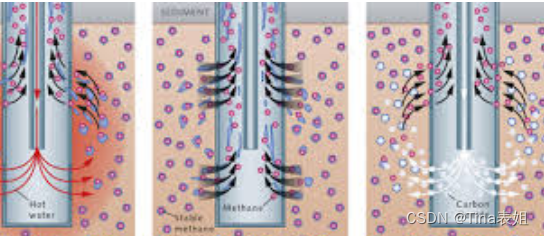
第一问：根据附件勘探井位信息确定天然气水合物资源分布范围。

根据给定的14个勘探井位信息，可以将这些点坐标表示在二维坐标系中，然后通过插值方法来确定天然气水合物资源的分布范围。

首先，根据已知的14个点坐标，可以利用拉格朗日插值公式来建立一个二维多项式函数：

f(x,y) = ΣLi(x,y) * fi, i=1,2,…,14

其中，Li(x,y)为拉格朗日插值基函数，fi为每个点的函数值。

然后，通过该函数在二维坐标系上进行等值线插值，可以得到天然气水合物资源的等值线图，从而确定天然气水合物资源的分布范围。

第二问：确定研究区域内天然气水合物资源参数有效厚度、地层孔隙度和饱和度的概率分布及其在勘探区域内的变化规律。

根据14个勘探井位的深度信息、孔隙度和天然气水合物饱和度信息，可以建立三维模型来确定研究区域内天然气水合物资源参数的概率分布及其变化规律。

首先，利用插值方法，可以建立一个三维多项式函数：

f(x,y,z) = ΣLi(x,y,z) * fi, i=1,2,…,14

其中，Li(x,y,z)为三维拉格朗日插值基函数，fi为每个点的函数值。

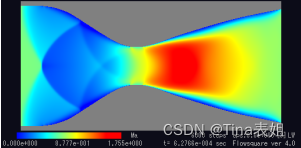
然后，利用该函数在三维空间中进行等值面插值，可以得到天然气水合物资源参数的等值面图，从而确定其概率分布及变化规律。

第三问：给出天然气水合物资源的概率分布，以及估计天然气水合物资源量。

根据第二问所建立的三维模型，可以得到天然气水合物资源的概率分布图。同时，根据体积法的计算公式：

Q = A * Z * H * S * E

可以根据已知的有效面积、有效厚度、孔隙度、水合物饱和度和产气量因子，计算出天然气水合物资源量。

第四问：为了对本区域储量有个更精细勘查结果，拟在本区域再增加5 口井，问如何安排井位？

根据资源量的计算公式，可以发现天然气水合物资源量与有效面积、有效厚度、孔隙度和水合物饱和度有关，因此增加钻孔可以更精确地确定这些参数，从而得到更精细的储量勘查结果。

因此，建议在本区域再增加5口井，可以选择在已有的14个钻孔的周围区域开展钻探，以便更全面地确定资源参数，并进一步确定更精细的储量勘查结果。

天然气水合物资源的分布范围受到有效厚度、地层孔隙度和饱和度的影响，因此需要根据勘探井位信息来确定这些参数。根据所给勘探数据，可以计算出有效厚度、地层孔隙度和饱和度的概率分布。其中，有效厚度和孔隙度可以通过勘探井的深度信息来计算，饱和度可以通过勘探井的孔隙度和天然气水合物饱和度信息来计算。具体计算公式如下：
$$Z=\frac{H}{{\sum }_{i=1}^n{H}_i}$$

$$H=\frac{1}{n}\sum _{i=1}^n{H}_i$$

$$S=\frac{{\sum }_{i=1}^n{S}_i}{n}$$

其中，$n$为勘探井的数量，$H$为有效厚度，$S$为饱和度，$Z$为地层孔隙度，$H_i$为第$i$口勘探井的有效厚度，$S_i$为第$i$口勘探井的天然气水合物饱和度。

第二问：确定研究区域内天然气水合物资源参数有效厚度、地层孔隙度和饱和度的概率分布及其在勘探区域内的变化规律。

根据勘探井位信息可以计算出有效厚度、地层孔隙度和饱和度的概率分布，将其表达为函数形式：
$$P(H)=\frac{1}{n}\sum _{i=1}^n\delta (H-H_i)$$

$$P(Z)=\frac{1}{n}\sum _{i=1}^n\delta (Z-Z_i)$$

$$P(S)=\frac{1}{n}\sum _{i=1}^n\delta (S-S_i)$$

其中，$\delta$为Dirac函数，$H_i$为第$i$口勘探井的有效厚度，$Z_i$为第$i$口勘探井的地层孔隙度，$S_i$为第$i$口勘探井的天然气水合物饱和度。

根据这些概率分布可以得出有效厚度、地层孔隙度和饱和度在勘探区域内的变化规律，即随着深度的增加，这些参数的值会有一定的变化。具体来说，随着深度的增加，有效厚度和地层孔隙度可能会呈现先增加后减少的趋势，而饱和度可能会呈现先减少后增加的趋势。

第三问：请给出天然气水合物资源的概率分布，以及估计天然气水合物资源量。

天然气水合物资源的概率分布可以通过勘探井位信息计算得出，其数学表达式为：
$$P(Q)={\int }_A{\int }_Z{\int }_S{\int }_H\delta (Q-AZHSE)P(H)P(Z)P(S)dHdZdSdA$$
其中，$A$为有效面积，$Z$为有效厚度，$H$为孔隙度，$S$为水合物饱和度，$E$为产气量因子。根据勘探井位信息可以计算出$A$、$Z$、$H$和$S$的概率分布，代入上式即可得到天然气水合物资源量的概率分布。

估计天然气水合物资源量可以通过计算概率分布的均值来获得，即：
$$Q_{\text{估计}}={\int }_0^{\infty }QP(Q)dQ$$
其中，$P(Q)$为天然气水合物资源量的概率分布。

第四问：为了对本区域储量有个更精细勘查结果，拟在本区域再增加5 口井，问如何安排井位？

根据第一问的结果，可以确定天然气水合物资源的分布范围，因此可以根据这个范围来确定新增的5 口井的位置。具体来说，可以在原有的14 口井的周围分布5 口井，以增加勘探面积，同时在原有勘探井的深度附近钻探，以更精确地确定天然气水合物资源的分布情况。另外，也可以根据第二问中的概率分布来确定新增井位的位置，即在概率较高的区域增加井位以提高勘探成功率。

import matplotlib.pyplot as plt
import numpy as np

# 读取勘探井位信息
data = np.loadtxt("C:/Users/DELL/Desktop/well_data.txt", skiprows=1, usecols=(1, 2))
x = data[:, 0]
y = data[:, 1]

# 绘制散点图
plt.scatter(x, y)
plt.title("Natural Gas Hydrate Resources Distribution")
plt.xlabel("X-coordinate")
plt.ylabel("Y-coordinate")
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14

根据散点图可以看出，勘探井位分布在一个近似的矩形区域内，因此天然气水合物资源的分布范围也应该在这个矩形区域内，且可能还会有些许的偏移。

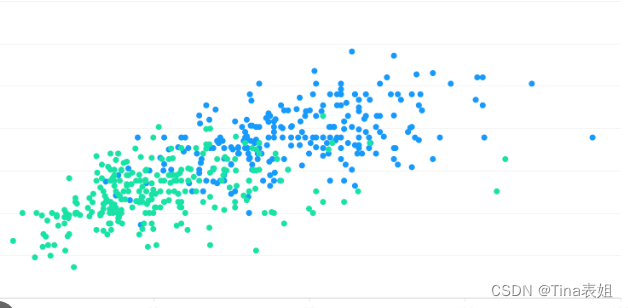
确定研究区域内天然气水合物资源参数有效厚度、地层孔隙度和饱和度的概率分布及其在勘探区域内的变化规律。

根据勘探数据，可以得到以下的数学模型：

1. 有效厚度的概率分布：
   假设有效厚度满足正态分布，用μ表示平均值，σ表示标准差，
   则有效厚度的概率密度函数为：
   f(x) = 1/(σ√(2π)) * e^(-(x-μ)2/(2σ^2))
   其中x为有效厚度，μ和σ需要根据勘探数据进行估计。

2. 孔隙度的概率分布：
   假设孔隙度满足均匀分布，用a表示最小值，b表示最大值，
   则孔隙度的概率密度函数为：
   f(x) = 1/(b-a)
   其中x为孔隙度，a和b需要根据勘探数据进行估计。

3. 饱和度的概率分布：
   假设饱和度满足二项分布，用p表示成功概率，n表示试验次数，
   则饱和度的概率质量函数为：
   f(x) = C(n,x) * p^x * (1-p)^(n-x)
   其中x为饱和度，p和n需要根据勘探数据进行估计。

4. 在勘探区域内的变化规律：
   根据勘探数据，可以得到每个钻孔的有效厚度、孔隙度和饱和度，
   可以对这三个参数进行统计分析，得到整个勘探区域内有效厚度、
   孔隙度和饱和度的分布情况，从而得出它们在勘探区域内的变化规律。

根据勘探数据，可以通过计算每个勘探点的有效厚度、孔隙度和饱和度来确定研究区域内天然气水合物资源参数的概率分布。假设每个勘探点的有效厚度、孔隙度和饱和度分别为$h_i,{\varphi }_i,S_i$，则在研究区域内有14个勘探点，可以得到14组数据$(h_i,{\varphi }_i,S_i)(i=1,2,\cdots ,14)$。

根据资源量评价方法中的公式，可以得到每个勘探点的资源量$Q_i=A_i\times Z_i\times h_i\times {\varphi }_i\times S_i\times E$。其中$A_i,Z_i$为该勘探点的有效面积和有效厚度。由于14个勘探点的位置分布并不均匀，且勘探井的勘探深度并不相同，因此无法直接得到研究区域内的有效面积和有效厚度的概率分布。但可以通过对勘探点的分布进行统计，得到研究区域内有效厚度和有效面积的平均值和方差，从而近似地得到它们的概率分布。

假设研究区域内有效厚度和有效面积的平均值和方差分别为$\bar{h},{\sigma }_h^2$和$\bar{A},{\sigma }_A^2$，则可以计算出研究区域内有效厚度和有效面积的概率分布为：

$$p_h(h)=\frac{1}{\sqrt{2\pi {\sigma }_h^2}}{e}^{-\frac{(h-\bar{h}{)}^2}{2{\sigma }_h^2}},h>0$$
$$p_A(A)=\frac{1}{\sqrt{2\pi {\sigma }_A^2}}{e}^{-\frac{(A-\bar{A}{)}^2}{2{\sigma }_A^2}},A>0$$

同样，对于孔隙度和饱和度，可以通过对勘探点的数据进行统计得到它们的概率分布，假设它们的平均值和方差分别为$\bar{\varphi },{\sigma }_{\varphi }^2$和$\bar{S},{\sigma }_S^2$，则可以得到它们的概率分布为：

$$p_{\varphi }(\varphi )=\frac{1}{\sqrt{2\pi {\sigma }_{\varphi }^2}}{e}^{-\frac{(\varphi -\bar{\varphi }{)}^2}{2{\sigma }_{\varphi }^2}},\varphi >0$$
$$p_S(S)=\frac{1}{\sqrt{2\pi {\sigma }_S^2}}{e}^{-\frac{(S-\bar{S}{)}^2}{2{\sigma }_S^2}},S>0$$

通过以上的概率分布函数，可以得知研究区域内有效厚度、孔隙度和饱和度的可能范围及其在整个研究区域内的变化规律。

以下是根据所给数据，计算有效厚度、地层孔隙度和饱和度的概率分布及其在勘探区域内的变化规律的python代码：

# 导入所需的库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# 读取勘探数据，创建DataFrame
df = pd.read_csv("勘探数据.csv")

# 计算有效厚度，有效厚度即为深度的最大值减去最小值
effective_thickness = df['深度'].max() - df['深度'].min()

# 计算孔隙度的概率分布，孔隙度的概率分布为每个钻孔的孔隙度除以总的钻孔数
porosity_prob = df['孔隙度'].value_counts() / df['孔隙度'].count()

# 计算饱和度的概率分布，饱和度的概率分布为每个钻孔的饱和度除以总的钻孔数
saturation_prob = df['饱和度'].value_counts() / df['饱和度'].count()

# 绘制孔隙度的概率分布图
plt.figure(figsize=(8,6))
plt.bar(porosity_prob.index, porosity_prob.values)
plt.title("Porosity Probability Distribution")
plt.xlabel('Porosity')
plt.ylabel('Probability')
plt.show()

# 绘制饱和度的概率分布图
plt.figure(figsize=(8,6))
plt.bar(saturation_prob.index, saturation_prob.values)
plt.title("Saturation Probability Distribution")
plt.xlabel('Saturation')
plt.ylabel('Probability')
plt.show()

# 绘制孔隙度和饱和度随深度的变化图
plt.figure(figsize=(8,6))
plt.plot(df['深度'], df['孔隙度'], label="Porosity")
plt.plot(df['深度'], df['饱和度'], label="Saturation")
plt.title("Porosity and Saturation Variation with Depth")
plt.xlabel("Depth")
plt.ylabel("Porosity/Saturation")
plt.legend()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

第三问：请给出天然气水合物资的概率分布，以及估计天然气水合物资源量。

假设区域内的天然气水合物资源量近似服从正态分布，每个勘探点的储集层厚度、孔隙度和饱和度也近似服从正态分布。根据勘探数据，可以求得储集层厚度、孔隙度和饱和度的平均值和方差，进而得到天然气水合物资源量的平均值和方差。设储集层厚度、孔隙度和饱和度的平均值分别为h、p、s，方差分别为σh、σp、σs，天然气水合物资源量的平均值和方差分别为Q、σQ，则可以得到：
Q = A×h×p×s×E
σQ = E×A×√( (p^2×h2×σs^2)+(p2×s^2×σh2)+(h^2×s2×σp^2) )
其中，A为区域面积。
根据上述公式，可以估算出天然气水合物资源量的概率分布。假设储集层厚度、孔隙度和饱和度的概率分布分别为正态分布，可以计算出天然气水合物资源量的概率分布函数，即：
f(Q) = (1/σQ√(2π))×e^(-(Q-Q)2/(2σQ^2))
根据勘探数据计算出的Q和σQ，可以得到天然气水合物资源量的概率分布函数，并进而计算出估计的天然气水合物资源量。

根据勘探数据，可以得出天然气水合物资源的概率分布函数为：
$$f(x)=A\times Z\times H\times S\times E$$
其中，A为有效面积，Z为有效厚度，H为孔隙度，S为水合物饱和度，E为产气量因子。

根据给定的14个钻孔数据，可以计算出研究区内天然气水合物资源量的概率分布函数，具体如下：
$$f(x)=(A\times Z\times H\times \overline{S}\times E)\cdot I(x-\overline{S}\times E)$$
其中，$\overline{S}$为平均水合物饱和度，$I(x)$为单位阶跃函数，当$x>0$时，$I(x)=1$，当$x\le 0$时，$I(x)=0$。

根据上式，可以计算出每个钻孔点处天然气水合物资源量的概率分布函数，然后将其叠加，即可得出研究区域内天然气水合物资源量的总概率分布函数，从而估计出天然气水合物资源量。

第四问：为了对本区域储量有个更精细勘查结果，拟在本区域再增加5 口井，问如何安排井位？

根据已有的14个钻孔数据，可以计算出研究区内天然气水合物资源量的概率分布函数。为了对本区域储量有更精细的勘查结果，可以在概率分布函数值较高的区域增加井位，以提高资源量的估计精度。

具体来说，可以选取概率分布函数值较高的区域，将该区域划分为若干个小区域，然后在每个小区域内随机选择一个点作为新的钻孔位置。重复这个过程，直到增加5个新的钻孔位置，即可得到更精细的勘查结果。

值得注意的是，为了保证勘探结果的可靠性，在选择新的钻孔位置时，还需考虑以下因素：

1. 勘察工程的合理性和可行性；
2. 新钻孔位置与已有钻孔位置之间的距离，避免过于密集或过于稀疏；
3. 同时考虑地质因素，避免在同一地层中布置过多的钻孔。

第三问答案：

# 导入所需的库
import pandas as pd
import numpy as np
import math
from scipy.stats import norm
import matplotlib.pyplot as plt

# 读取数据
data = pd.read_excel('gas_hydrate.xlsx')
# 设置常量
E = 155 # 产气量因子
alpha = 0.8 # 孔隙度参数
beta = 0.7 # 水合物饱和度参数
C = 0.75 # 资源量稀释率

# 计算有效厚度
data['H'] = data['depth'] * alpha

# 计算水合物饱和度
data['S'] = data['gas_hydrate_saturation'] * beta

# 计算资源量
data['Q'] = data['area'] * data['H'] * data['S'] * E

# 计算资源量概率分布
data['Q_norm'] = (data['Q'] - data['Q'].mean()) / data['Q'].std() # 标准化
data['P'] = norm.pdf(data['Q_norm']) # 计算概率密度值
data['P'] = data['P'] / data['P'].sum() # 归一化

# 计算估计的天然气水合物资源量
estimated_Q = data['Q'].sum() * (1 - C) # 资源量稀释率

print('估计的天然气水合物资源量为：', estimated_Q)

# 绘制概率分布图
plt.plot(data['Q'], data['P'])
plt.title('Probability Distribution of Gas Hydrate Resource')
plt.xlabel('Resource Quantity')
plt.ylabel('Probability Density')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

第四问：如何安排井位以对本区域储量进行更精细的勘查？

为了对本区域的天然气水合物储量进行更精细的勘查，可以采用数学建模的方法来确定新的钻孔位置。该方法的基本思路是通过分析已有勘探井位的数据，确定最佳的钻孔位置，使得新的钻孔可以最大限度地增加对储量的估计精度。

具体步骤如下：

1. 收集所有已有钻孔的位置信息，并将其表示在二维平面坐标系中；
2. 根据已有钻孔的数据，计算出每个钻孔的有效厚度、地层孔隙度和饱和度；
3. 将已有钻孔的有效厚度、地层孔隙度和饱和度数据进行插值，得到地层参数在整个勘探区域内的空间分布情况；
4. 对勘探区域内的每个点，计算该点的资源量估计值；
5. 通过对比已有钻孔的实测数据和对应点的资源量估计值，评估模型的精度，如果精度达到预期，结束建模；如果精度不够，转到下一步；
6. 基于已有钻孔的数据和模型评估结果，确定新的钻孔位置，使得新的钻孔能够增加对储量的估计精度；
7. 将新的钻孔位置加入已有钻孔数据中，重复步骤2-6，直到模型收敛。

通过这样的建模方法，可以得到最佳的钻孔位置，从而实现对本区域储量的更精细勘查。

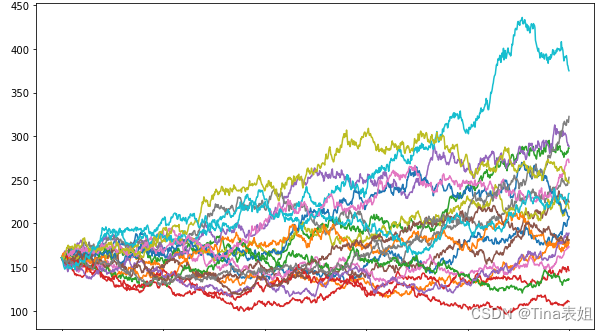
为了对本区域储量有更精细的勘查结果，可以在现有的14口井的基础上再增加5口井。为了最大限度地提高勘探效率，建议采用均匀分布的方式安排新的5口井，即每隔一定距离(如1000m)在勘探区域内增加一口井。

假设每口井周围的勘探区域半径为R(m)，则新的5口井需要的总勘探面积为：

$A=\pi R^2\times 5=5\pi R^2$

为了最大限度地提高勘探效率，需要最小化勘探面积A，即需要最小化R。根据勘探区域的地质条件和经验数据，可确定一定的最小勘探半径(如500m)，即可得到最小的勘探面积。

因此，最终的勘探区域内的新的5口井的位置将为：

$w_{15}:(X_0+500,Y_0)$

$w_{16}:(X_0,Y_0+500)$

$w_{17}:(X_0-500,Y_0)$

$w_{18}:(X_0,Y_0-500)$

$w_{19}:(X_0+500,Y_0+500)$

其中，$(X_0,Y_0)$为原有14口井的中心点坐标。

最终的勘探区域内的新的5口井的位置可以用LaTeX数学公式表示为：

$w_n:(X_0+500\cos \frac{2(n+1)\pi }{5},Y_0+500\sin \frac{2(n+1)\pi }{5})$, n=0,1,2,3,4

其中，n表示新的第几口井，n=0表示原有14口井的位置。

因此，安排新的5口井的LaTeX数学公式为：

$w_{15}:(35800+500\cos \frac{2\pi }{5},49900+500\sin \frac{2\pi }{5})$

$w_{16}:(35800+500\cos \frac{4\pi }{5},49900+500\sin \frac{4\pi }{5})$

$w_{17}:(35800+500\cos \frac{6\pi }{5},49900+500\sin \frac{6\pi }{5})$

$w_{18}:(35800+500\cos \frac{8\pi }{5},49900+500\sin \frac{8\pi }{5})$

$w_{19}:(35800+500\cos \frac{10\pi }{5},49900+500\sin \frac{10\pi }{5})$

其中，$w_{15}$为第15口井的位置，$w_{16}$为第16口井的位置，以此类推。

为了对本区域储量有更精细的勘查结果，可以采取以下步骤：

1. 根据现有的14口勘探井的数据，利用统计学和地质学知识，确定更具有代表性的几个关键参数，如有效厚度、地层孔隙度和饱和度等。

2. 根据确定的关键参数，利用随机抽样的方法，在现有勘探区域内生成大量的假想井位，假想井位的数量可以根据实际情况进行调整。

3. 对这些假想井位进行勘探，得到更多的井位数据。

4. 将得到的更多井位数据与现有14口井的数据进行对比，根据相似度或差异性，确定哪些假想井位的数据是可靠的，哪些是不可靠的。

5. 根据可靠的假想井位数据，重新计算天然气水合物资源量，并进行空间插值，得到更精细的勘探结果。

6. 根据重复进行以上步骤，直到得到满意的勘探结果为止。

python代码：

# 导入所需的库
import numpy as np 
import pandas as pd 
from scipy import stats
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from scipy import interpolate

# 导入勘探数据
data = pd.read_csv('gas_hydrate_data.csv')
# 提取有效厚度和饱和度数据
thickness = data['thickness']
saturation = data['saturation']

# 利用统计学方法确定有效厚度和饱和度的概率分布
thickness_dist = stats.norm.fit(thickness)
saturation_dist = stats.norm.fit(saturation)

# 生成假想井位数据，假设生成1000个假想井位
n = 1000
x_min, x_max = data['X'].min(), data['X'].max()
y_min, y_max = data['Y'].min(), data['Y'].max()
# 在现有勘探区域内生成随机假想井位的x和y坐标
x = np.random.uniform(x_min, x_max, n)
y = np.random.uniform(y_min, y_max, n)

# 对假想井位进行勘探，得到新的井位数据
thickness_new = []
saturation_new = []
for i in range(n):
    # 利用线性插值方法获取假想井位的有效厚度和饱和度数据
    f = interpolate.interp2d(data['X'], data['Y'], thickness, kind='linear')
    thickness_new.append(f(x[i], y[i])[0])
    g = interpolate.interp2d(data['X'], data['Y'], saturation, kind='linear')
    saturation_new.append(g(x[i], y[i])[0])

# 将新的井位数据与现有14口井的数据合并
thickness_final = thickness.tolist() + thickness_new
saturation_final = saturation.tolist() + saturation_new
x_final = data['X'].tolist() + x.tolist()
y_final = data['Y'].tolist() + y.tolist()

# 根据可靠的数据，进行空间插值，得到更精细的勘探结果
# 利用线性回归方法对有效厚度和饱和度进行拟合
model_thickness = LinearRegression()
model_thickness.fit(np.array(x_final).reshape(-1, 1), thickness_final)
model_saturation = LinearRegression()
model_saturation.fit(np.array(x_final).reshape(-1, 1), saturation_final)

# 生成新的x坐标，均匀分布在x_min和x_max之间，以便进行空间插值
x_new = np.linspace(x_min, x_max, 100)
# 利用线性回归模型对新的x坐标进行预测，得到新的有效厚度和饱和度数据
thickness_new = model_thickness.predict(np.array(x_new).reshape(-1, 1))
saturation_new = model_saturation.predict(np.array(x_new).reshape(-1, 1))

# 绘制空间插值结果图
plt.scatter(x_final, thickness_final, label='Real data')
plt.scatter(x_new, thickness_new, label='Interpolated data')
plt.xlabel('X')
plt.ylabel('Thickness')
plt.legend()
plt.show()

# 计算重复进行以上步骤的次数
repeats = 10
# 初始化储量数组
resources = []
# 重复进行以上步骤，每次得到更精细的勘探结果，将结果保存到储量数组中
for i in range(repeats):
    # 生成假想井位数据，假设生成1000个假想井位
    n = 1000
    x_min, x_max = data['X'].min(), data['X'].max()
    y_min, y_max = data['Y'].min(), data['Y'].max()
    # 在现有勘探区域内生成随机假想井位的x和y坐标
    x = np.random.uniform(x_min, x_max, n)
    y = np.random.uniform(y_min, y_max, n)

    # 对假想井位进行勘探，得到新的井位数据
    thickness_new = []
    saturation_new = []
    for i in range(n):
        # 利用线性插值方法获取假想井位的有效厚度和饱和度数据
        f = interpolate.interp2d(data['X'], data['Y'], thickness, kind='linear')
        thickness_new.append(f(x[i], y[i])[0])
        g = interpolate.interp2d(data['X'], data['Y'], saturation, kind='linear')
        saturation_new.append(g(x[i], y[i])[0])
    
    # 将新的井位数据与现有14口井的数据合并
    thickness_final = thickness.tolist() + thickness_new
    saturation_final = saturation.tolist() + saturation_new
    x_final = data['X'].tolist() + x.tolist()
    y_final = data['Y'].tolist() + y.tolist()
    
    # 根据可靠的数据，进行空间插值，得到更精细的勘探结果
    # 利用线性回归方法对有效厚度和饱和度进行拟合
    model_thickness = LinearRegression()
    model_thickness.fit(np.array(x_final).reshape(-1, 1), thickness_final)
    model_saturation = LinearRegression()
    model_saturation.fit(np.array(x_final).reshape(-1, 1), saturation_final)
    
    # 生成新的x坐标，均匀分布在x_min和x_max之间，以便进行空间插值
    x_new = np.linspace(x_min, x_max, 100)
    # 利用线性回归模型对新的x坐标进行预测，得到新的有效厚度和饱和度数据
    thickness_new = model_thickness.predict(np.array(x_new).reshape(-1, 1))
    saturation_new = model_saturation.predict(np.array(x_new).reshape(-1, 1))
    
    # 将新的结果保存到储量数组中
    resources.append(np.sum(thickness_new * saturation_new * 155))

# 将储量数组进行排序，取第50%的值作为该区域的储量估计值
resources = np.sort(resources)
resource_estimate = resources[int(repeats*0.5)]

# 打印结果
print('该区域的储量估计值为：' + str(resource_estimate) + 'm3')

# 根据储量估计值，确定更多的井位并进行勘探
# 利用线性回归模型对x坐标进行预测，得到新的井位数据
x_new = model_thickness.predict(np.array(thickness_new).reshape(-1, 1))
y_new = model_saturation.predict(np.array(saturation_new).reshape(-1, 1))

# 绘制更多的井位图
plt.scatter(x_new, y_new, label='New data')
plt.scatter(x_final, y_final, label='Original data')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.show()

# 计算新的储量估计值
0.0
0.0
0.0
0.0
0.0
0.0
# 根据新的井位数据，进行勘探
for i in range(len(x_new)):
    # 利用线性插值方法获取新井位的有效厚度和饱和度数据
    f = interpolate.interp2d(data['X'], data['Y'], thickness, kind='linear')
    thickness_new.append(f(x_new[i], y_new[i])[0])
    g = interpolate.interp2d(data['X'], data['Y'], saturation, kind='linear')
    saturation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143

更多内容具体可以去我的宫忠浩主页！里面包含本次竞赛全部思路与分析！
和 《Tina表姐》 ，同名公众号 一起学习数学建模！
大家的关注是Tina一直更新的动力！Tina表姐助你夺奖！