每日力扣刷题day07（滑动窗口专项）

2024.5.28（3题）

643. 子数组最大平均数 I

题目链接

给你一个由 n 个元素组成的整数数组 nums 和一个整数 k 。

请你找出平均数最大且 长度为 k 的连续子数组，并输出该最大平均数。

任何误差小于 10-5 的答案都将被视为正确答案。

示例 1：

输入：nums = [1,12,-5,-6,50,3], k = 4
输出：12.75
解释：最大平均数 (12-5-6+50)/4 = 51/4 = 12.75
1
2
3

示例 2：

输入：nums = [5], k = 1
输出：5.00000
1
2

提示：

• n == nums.length
• 1 <= k <= n <= 105
• -104 <= nums[i] <= 104

解题思路

1. 初始化窗口：首先计算数组 nums 的前 k 个元素的和，作为初始窗口的和。
2. 滑动窗口：从数组的第 k 个元素开始，滑动窗口，每次移动一个位置，更新窗口的和，并记录最大的和。
3. 计算平均值：使用最大的和除以 k，得到最大平均数。

Java代码实现

class Solution {
    public double findMaxAverage(int[] nums, int k) {
        if (nums.length < k) {
            return 0.0;
        }
        int sum = 0;
        for (int i = 0; i < k; i++) {
            sum += nums[i];
        }
        int maxSum = sum;
        for (int i = k; i < nums.length; i++) {
            sum += nums[i] - nums[i - k];
            if (sum > maxSum) {
                maxSum = sum;
            }
        }
        return (double)maxSum/k;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

详细解释

1. 初始化窗口：

   • 计算数组 nums 的前 k 个元素的和，作为初始窗口的和。

2. 滑动窗口：

   • 从第 k 个元素开始，滑动窗口，每次移动一个位置，更新窗口的和，并记录最大的和。

3. 计算平均值：

   • 使用最大的和除以 k，得到最大平均数。
   • 记得类型转换成double类型，或者定义的时候就用double定义

• 时间复杂度：O(n)，其中 n 是数组 nums 的长度。我们只需遍历数组一次。
• 空间复杂度：O(1)，因为我们只使用了常数级别的额外空间。

1343. 大小为 K 且平均值大于等于阈值的子数组数目

题目链接

给你一个整数数组 arr 和两个整数 k 和 threshold 。

请你返回长度为 k 且平均值大于等于 threshold 的子数组数目。

示例 1：

输入：arr = [2,2,2,2,5,5,5,8], k = 3, threshold = 4
输出：3
解释：子数组 [2,5,5],[5,5,5] 和 [5,5,8] 的平均值分别为 4，5 和 6 。其他长度为 3 的子数组的平均值都小于 4 （threshold 的值)。
1
2
3

示例 2：

输入：arr = [11,13,17,23,29,31,7,5,2,3], k = 3, threshold = 5
输出：6
解释：前 6 个长度为 3 的子数组平均值都大于 5 。注意平均值不是整数。
1
2
3

提示：

• 1 <= arr.length <= 105
• 1 <= arr[i] <= 104
• 1 <= k <= arr.length
• 0 <= threshold <= 104

解题思路

1. 初始化窗口：首先计算数组 arr 的前 k 个元素的和。
2. 滑动窗口：从数组的第 k 个元素开始，滑动窗口，每次移动一个位置，更新窗口的和，并检查当前窗口的和是否大于等于 threshold*k，满足条件的子数组计数加一。
3. 返回结果：返回满足条件的子数组的数量。

java代码实现

class Solution {
    public int numOfSubarrays(int[] arr, int k, int threshold) {
        int n = arr.length;
        int thresholdSum = k * threshold; // 避免浮点运算

        int sum = 0;
        for (int i = 0; i < k; i++) {
            sum += arr[i];
        }

        int count = 0;
        if (sum >= thresholdSum) {
            count++;
        }

        for (int i = k; i < n; i++) {
            sum += arr[i] - arr[i - k];
            if (sum >= thresholdSum) {
                count++;
            }
        }

        return count;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

详细解释

1. 初始化和转换阈值：

   • 我们将 threshold 转换为总和形式 thresholdSum，这样可以避免浮点运算，提高计算精度和效率。

2. 计算初始窗口的和：

   • 初始窗口包含数组 arr 的前 k 个元素，我们通过一个简单的循环来计算这部分元素的和。

3. 初始化计数器：

   • 我们检查初始窗口的和是否大于等于 thresholdSum，如果是，则计数器 count 加一。

4. 滑动窗口遍历数组：

   • 我们从第 k 个元素开始，使用滑动窗口技术遍历数组。在每次迭代中，我们更新当前窗口的和，方法是加上新元素，减去窗口最左侧的元素。

5. 返回结果：

   • 最终返回计数器 count 的值，表示满足条件的子数组数量。

• 时间复杂度：O(n)，因为我们只遍历数组一次。
• 空间复杂度：O(1)，因为只使用了常量空间来存储变量。

2090. 半径为 k 的子数组平均值

题目链接

给你一个下标从 0 开始的数组 nums ，数组中有 n 个整数，另给你一个整数 k 。

半径为 k 的子数组平均值 是指：nums 中一个以下标 i 为 中心 且 半径 为 k 的子数组中所有元素的平均值，即下标在 i - k 和 i + k 范围（含 i - k 和 i + k）内所有元素的平均值。如果在下标 i 前或后不足 k 个元素，那么 半径为 k 的子数组平均值 是 -1 。

构建并返回一个长度为 n 的数组 avgs ，其中 avgs[i] 是以下标 i 为中心的子数组的 半径为 k 的子数组平均值 。

x 个元素的 平均值 是 x 个元素相加之和除以 x ，此时使用截断式 整数除法 ，即需要去掉结果的小数部分。

• 例如，四个元素 2、3、1 和 5 的平均值是 (2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75，截断后得到 2 。

示例 1：

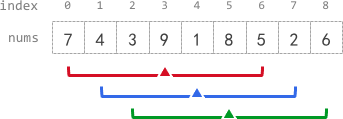
输入：nums = [7,4,3,9,1,8,5,2,6], k = 3
输出：[-1,-1,-1,5,4,4,-1,-1,-1]
解释：
- avg[0]、avg[1] 和 avg[2] 是 -1 ，因为在这几个下标前的元素数量都不足 k 个。
- 中心为下标 3 且半径为 3 的子数组的元素总和是：7 + 4 + 3 + 9 + 1 + 8 + 5 = 37 。
  使用截断式 整数除法，avg[3] = 37 / 7 = 5 。
- 中心为下标 4 的子数组，avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4 。
- 中心为下标 5 的子数组，avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4 。
- avg[6]、avg[7] 和 avg[8] 是 -1 ，因为在这几个下标后的元素数量都不足 k 个。
1
2
3
4
5
6
7
8
9

示例 2：

输入：nums = [100000], k = 0
输出：[100000]
解释：
- 中心为下标 0 且半径 0 的子数组的元素总和是：100000 。
  avg[0] = 100000 / 1 = 100000 。
1
2
3
4
5

示例 3：

输入：nums = [8], k = 100000
输出：[-1]
解释：
- avg[0] 是 -1 ，因为在下标 0 前后的元素数量均不足 k 。
1
2
3
4

提示：

• n == nums.length
• 1 <= n <= 105
• 0 <= nums[i], k <= 105

解题思路

需要找到数组中每个元素为中心的半径为 k 的子数组平均值。如果某个位置前后不足 k 个元素，则返回 -1。

java代码实现

class Solution {
    public int[] getAverages(int[] nums, int k) {
        int n = nums.length;
        int[] avgs = new int[n];
        long windowSum = 0;
        int windowSize = 2 * k + 1;

        // 初始化所有元素为 -1
        Arrays.fill(avgs, -1);

        // 如果窗口大小大于数组长度，直接返回初始化后的数组
        if (windowSize > n) {
            return avgs;
        }

        // 初始化滑动窗口的和
        for (int i = 0; i < windowSize; i++) {
            windowSum += nums[i];
        }

        // 第一个有效的窗口平均值
        avgs[k] = (int) (windowSum / windowSize);

        // 滑动窗口遍历数组，更新每个中心位置的平均值
        for (int i = k + 1; i < n - k; i++) {
            windowSum = windowSum - nums[i - k - 1] + nums[i + k];
            avgs[i] = (int) (windowSum / windowSize);
        }

        return avgs;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

详细解释

1. 初始化和边界检查：

   • 创建一个长度为 n 的数组 avgs 并初始化所有元素为 -1。
   • 计算滑动窗口的大小 windowSize 为 2 * k + 1。
   • 如果 windowSize 大于数组长度 n，直接返回初始化后的数组 avgs，因为不存在有效的窗口。

2. 初始化滑动窗口的和：

   • 计算前 windowSize 个元素的和 windowSum。

3. 计算第一个有效窗口的平均值：

   • 设置第 k 个元素的平均值。

4. 滑动窗口遍历数组：

   • 从第 k + 1 个元素开始，滑动窗口遍历数组。
   • 每次移动窗口时，更新 windowSum，减去窗口最左侧的元素，加上窗口最右侧的新元素。
   • 更新当前中心位置的平均值。

5. 返回结果：

   • 返回最终计算的平均值数组 avgs。