AES_ECB算法原理及C语言实现_aes算法实现c语言

1、AES_ECB算法基本原理

AES_ECB 算法是AES算法几种模式中最简单一种。AES支持不同长度的密钥长度：128bit(16字节)，192bit(24字节)，256bit(32字节)。本文以128bit为例进行说明。
算法流程如下：

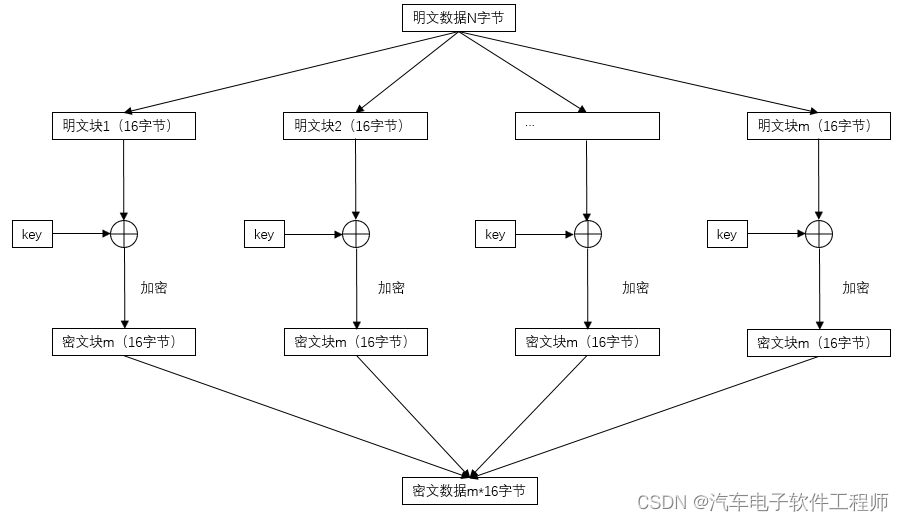
第一步将输入数据进行分组，每组16字节，注意，如果最后一个块不满16字节，则需要进行填充，填充方法如下：
如果最后一个块只有x个字节，则在最后一个块后面填充16-x个16-x，比如最后一个块只有7个字节：
[byte1, byte2, byte3, byte4, byte5, byte6, byte7]
那么就在在已经存在的七个字节后面填充9个0x09凑足16字节:
[byte1, byte2, byte3, byte4, byte5, byte6, byte7, 0x09, 0x09, 0x09, 0x09, 0x09, 0x09, 0x09, 0x09, 0x09]
第二步使用密钥对每一个分组好的明文块加密，就得到加密后的密文块，然后将得到的密文块按照顺序拼接起来，就得到加密后的密文块；整个AES加密算法最核心的就是此步骤中的加密的算法，第二节详细介绍；

2、加密算法介绍

加密算法详细过程见下图：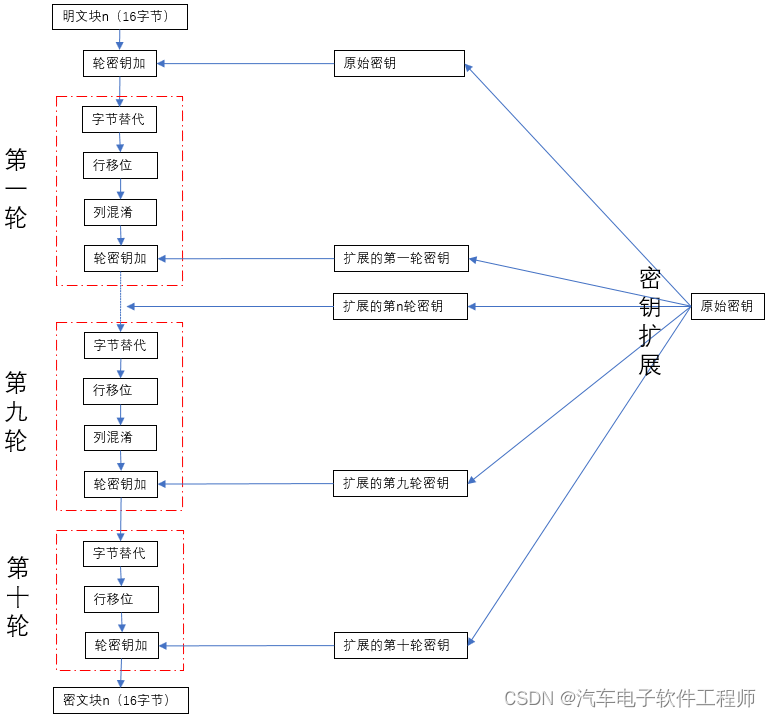
整个加密算法中最重要的是以下四个步骤：
1.轮密钥加（个人认为不应该叫加，应该叫异或才对）；
2.字节替代（也叫S盒替换），说白了就是用一个特定矩阵中的数据替换现有矩阵中的数据，详细后文介绍；
3.行移位，可以简单理解为把一个行数组循环左移N个字节，比如将数组[byte1, byte2, byte3, byte4]左移一个字节后变成[byte4，byte1, byte2, byte3]
4.列混淆，就是用指定矩阵与前一步的输出进行行列式乘法（特定矩阵左乘前一步的输出），后文会详细介绍；
对每一个块要进行10轮计算，每一轮都要进行上面四个步骤，然后每一轮的输出就是下一轮的输入，每一轮中每个步骤的输出，都是下一个步骤的输入，最后一轮的输出就是加密后的密文；需要注意的是第一轮之前需要额外进行一次轮密钥加，最后一轮中不进行列混淆；

上图中进行第一轮循环之前额外进行了一次轮密钥加，使用的是原始密钥；然后后面的十轮循环中的轮密钥加使用的是扩展密钥，每一轮的密钥都不同，扩展密钥是使用特定算法，用原始密钥扩展出来的，所以叫扩展密钥，扩展密钥的算法下文会首先介绍；

2.1 扩展密钥算法

需要说明的是本文是使用16字节密钥，因此可以将密钥看成是4x4矩阵，为什么要这么看呢，因为扩展密钥的算法以及前面讲的每一轮的加密计算都可以看作是对4x4矩阵的操作，方便后面大家理解；
比如原始密钥是[A0, A1, A2, A3, A4, A5, A6, A7, A8, A9, A10, A11, A12, A13, A14, A15]，那么将密钥重新排列为4x4矩阵，注意要按顺序竖着排：

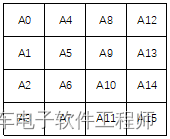
密钥的扩展就是基于原始密钥4x4矩阵再扩展出10个4x4这样的矩阵，然后在前面讲的每一轮加密的过程中轮密钥加的时候需要按顺序使用扩展出来的密钥；比如扩展出来的第一轮密钥如下：

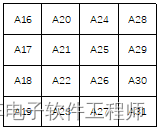
那么第一轮加密中的轮密钥加操作就要使用这一组密钥；
那么最后一轮加密中的轮密钥加操作就要使用最后一组扩展密钥：

密钥扩展算法如下图：

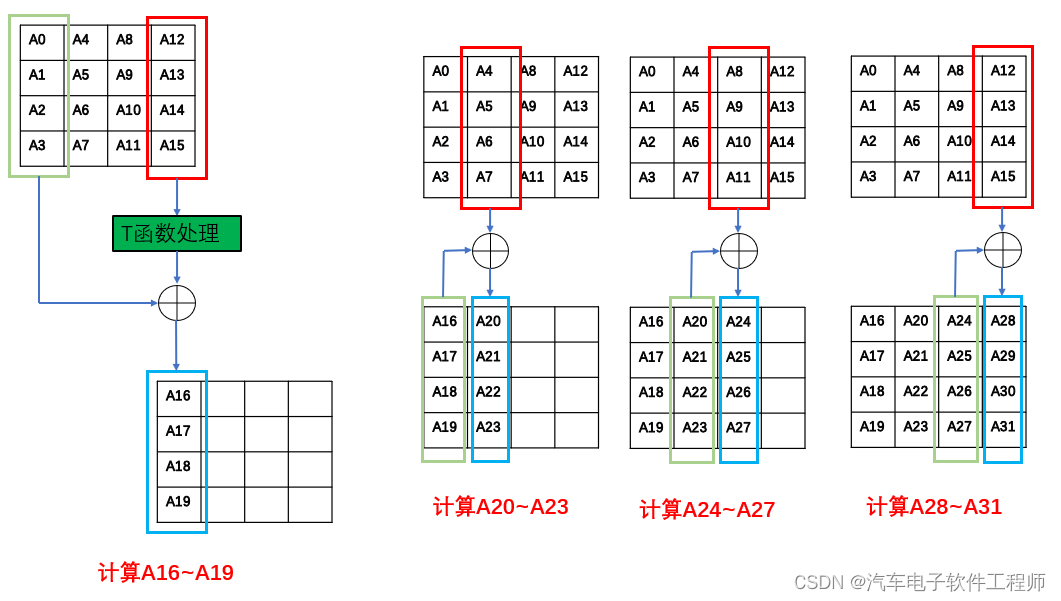
前面讲过了每一轮的密钥都可以看成是4x4的矩阵，原始密钥是已知的，可以看成是第0轮的密钥，第一轮的密钥只跟第0轮密钥相关，也就是用0轮密钥推导出第1轮密钥，后面的以此类推，用第1轮密钥推导出第2轮的密钥，用第2轮密钥推导出第3轮的密钥。
在上图中以第一轮的密钥推到为例，其他轮密钥推导方法是一模一样的；
第一轮密钥的计算中，除了第0列（A16~A19）外，其他三列的方法都一样，比如第1列的值就等于第0列的值与第0轮密钥的第1列相异或，可以理解成如下：
A20 = A4^A16
A21 = A5^A17
A22 = A6^A18
A23 = A7^A19
为了书写方便，记为（A20, A21, A22, A23）= (A4, A5, A6, A7)^(A16, A17, A18, A19)

第2列的值就等于第1列的值与第0轮密钥的第1列的值相异或：
（A24, A25, A26, A27）= (A8, A9, A10, A11)^(A20, A21, A22, A23)

第3列的值就等于第2列的值与第0轮密钥的第2列的值相异或：
（A28, A29, A30, A31）= (A12, A13, A14, A15)^(A24, A25, A26, A27)

第0列只是多了一步T函数的处理，将(A12, A13, A14, A15)经过T函数处理后的结果与(A0, A1, A2, A3)相异或：
(A16, A17, A18, A19)= (A0, A1, A2, A3)^ T{ (A12, A13, A14, A15)}

T函数处理分为3个步骤：
1.字节循环左移
相当于就是把[A12, A13, A14, A15]看成是一个一维数组，然后循环左移一个字节为[A13, A14, A15, A12];
2.字节替代
跟第一节中每一轮加密过程中的字节替代是一模一样的操作，就是把字节循环左移得到的结果通过查表，然后替换成另外的值，结果也也可以看作是一个1x4的数组；
3.与轮常量异或；
首先要说的是轮常量可以看作是一个10*4的二维数组，轮常量异或就是将字节替代后得到的1x4的数组，每个元素都与轮常量中的对应行中的四个元素进行异或，得到的也是一个1x4的数组；轮常量的值是定值：
Rcon[10][4] =
[
[ 0x01, 0x00, 0x00, 0x00 ],
[ 0x02, 0x00, 0x00, 0x00 ],
[ 0x04, 0x00, 0x00, 0x00 ],
[ 0x08, 0x00, 0x00, 0x00 ],
[ 0x10, 0x00, 0x00, 0x00 ],
[ 0x20, 0x00, 0x00, 0x00 ],
[ 0x40, 0x00, 0x00, 0x00 ],
[ 0x80, 0x00, 0x00, 0x00 ],
[ 0x1B, 0x00, 0x00, 0x00 ],
[ 0x36, 0x00, 0x00, 0x00 ],
]
然后在用原始密钥推导第一轮密钥的时候，使用[ 0x01, 0x00, 0x00, 0x00 ];
在用第一轮密钥推导第二轮密钥的时候，使用[ 0x02, 0x00, 0x00, 0x00 ]；
以此类推；
至此密钥扩展的算法就结束了；

2.2 轮密钥加

轮密钥加非常好理解，可以把输入看成是4x4的矩阵，然后与使用的密钥（也是4x4的矩阵）对应位置上的元素进行异或就可以了

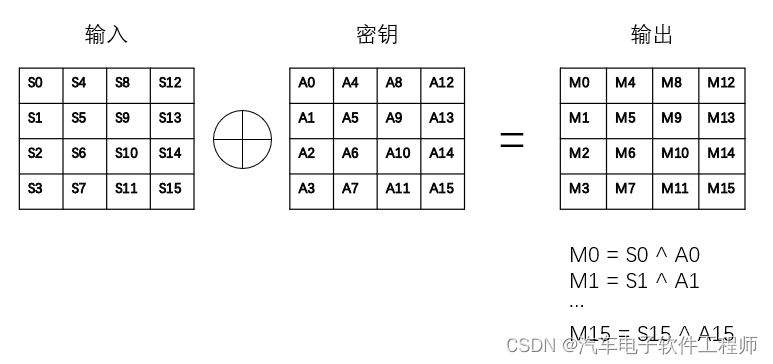
2.3字节替代

字节替代也非常简单，就是取出4x4的二维数组中每个元素的高四位和第四位，然后高四位作行，第四位作列，在S盒中（可以理解成16*16的二维数组）查找，用查找出来的值替换原来的元素；
S盒是AES算法已经定义好的一个表，如下：

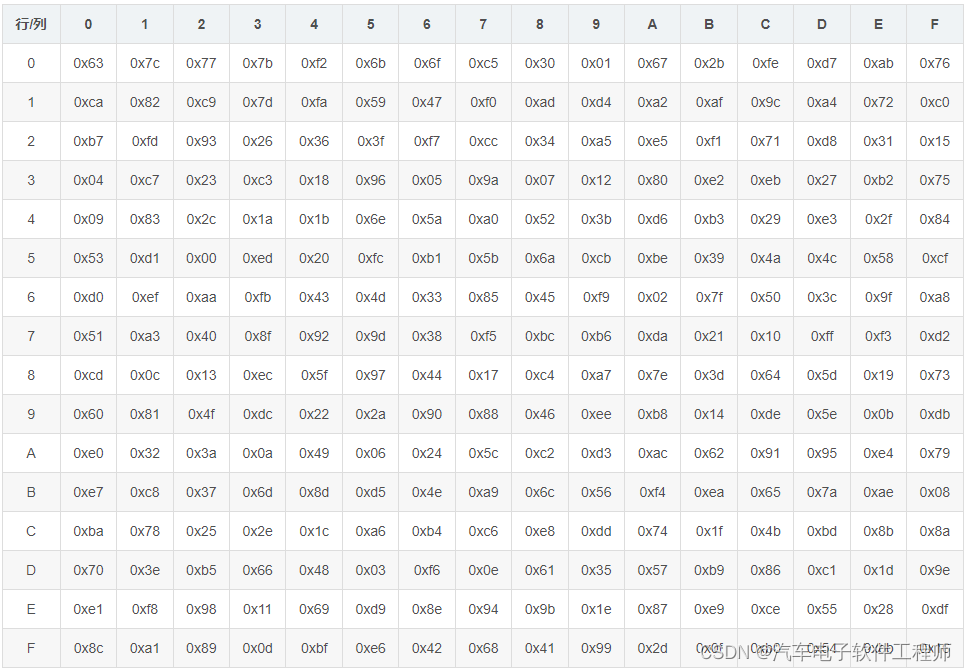
比如一个4x4的数组,数组名是array, array[0][0] = 0x44, 那么S盒中第四行第四列的数据为0x1b，那么通过S盒变换后，array[0][0] = 0x1b;

2.4行移位

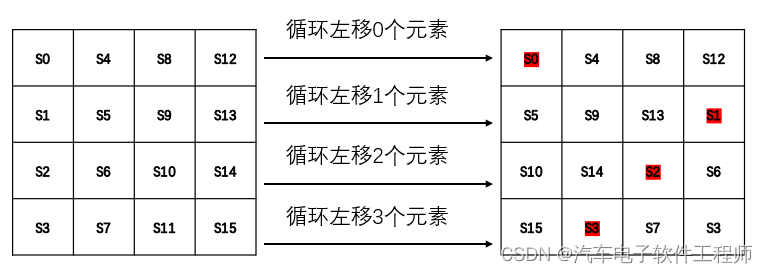
就是把4x4矩阵中的数据按照如下放下进行移位操作：
4x4矩阵第0行数据保持原样；
4x4矩阵第1行数据循环左移1个元素，即第0个元素变为第3个元素，第1个元素变为第0个元素，第2个元素变为第1个元素，第3个元素变为第2个元素；
4x4矩阵第2行数据循环左移2个元素，即第0个元素变为第2个元素，第1个元素变为第3个元素，第2个元素变为第0个元素，第3个元素变为第1个元素；
4x4矩阵第3行数据循环左移3个元素，即第0个元素变为第1个元素，第1个元素变为第2个元素，第2个元素变为第3个元素，第3个元素变为第0个元素；
示意图如下：

2.5列混淆

能这篇文章的人应该都学过线性代数，这里我们要提一下线性代数中的矩阵乘法，比如一个4x4的矩阵跟列外一个4x4的矩阵相乘，得到的也是一个4x4的矩阵：

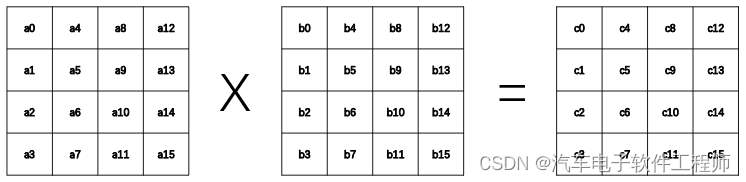
用Cij表示结果矩阵中的数据，则
Cij = Ai0B0j + Ai1B1j + Ai2B2j + Ai3B3j
列混淆的操作与行与矩阵的乘法非常相似，只不过有几点不一样：
1.左乘的矩阵是规定好了的，即上述矩阵乘法中的a0~a15的值是固定的；

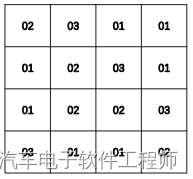
2.计算Cij的过程中的加法换成了异或，乘法操作换成了GF(2^8)上的二元运算（稍后再详细介绍GF(2 ^ 8)），我们把GF(2 ^ 8)上的乘法记为GF(a,b), 因此Cij的计算则变为：
Cij = GF(Ai0, B0j) ^ GF(Ai1, B1j) ^ GF(Ai2, B2j) ^ GF(Ai3, B3j)

下面来详细介绍GF(2^8)上的乘法运算：
有如下一个单字节数据：
B = b7b6b5b4b3b2b1b0, 其中b7是B的最高位，b0是B的最低位；
上文中已经讲过了，左乘的矩阵是固定的，其中只有01，02，03三个值，
因此我们只讨论GF(01, B), GF(02, B), GF(03, B)
GF(01, B)很简单就等于B： GF(01, B) = B;
GF(02, B)就需要分开讨论：
当b7=0时，GF(02, B) = B<<1, 即把B左移一位，最低位补0；
当b7=1时，GF(02, B) = (B<<1)^0x1B, 即先把B左移一位，最低位补0后，再与0x1B异或；
那么GF(03, B) = GF((02^01), B) = GF(02, B) ^ GF(01, B)

举个例子，比如列混淆输入矩阵为：

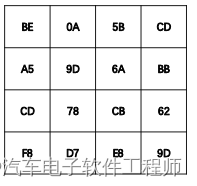
那么

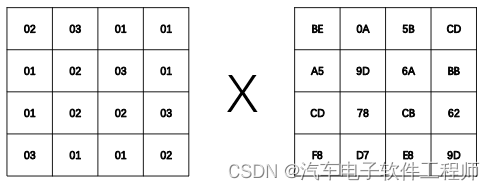
输出矩阵矩阵记为C, 用i,j表示矩阵的行和列，那么C的第一行数据计算过程如下：
C00 = GF(02, BE) ^ GF(01,A5) ^ GF(01, CD) ^ GF(03, F8)
C01 = GF(02, 0A) ^ GF(01,9D) ^ GF(01, 78) ^ GF(03, D7)
C02 = GF(02, 5B) ^ GF(01,6A) ^ GF(01, CB) ^ GF(03, E8)
C03 = GF(02, CD) ^ GF(01,BB) ^ GF(01, 62) ^ GF(03, 9D)

至此AES_ECB算法中的主要类容都已经介绍完了，下面以key长度为128bit为例，用C语言实现各个部分；

3、C语言实现AES_128 ECB

3.1 C语言实现扩展密钥

先直接上代码

static void key_Externed(uint8_t input_Key[][4])
{
   
    uint8_t i = 0;
    uint8_t k,j;
    uint8_t tmp[4];
    for(i=1;i<11;i++)
    {
   
        for(j=0;j<4;j++)
        {
   
            if(j==0)
            {
   
            	//T函数处理第一步，字节左移
                tmp[0] = input_Key[4*(i-1)+1][3];
                tmp[1] = input_Key[4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17