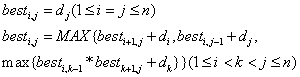贪心详解_什么是贪心策略

一、 贪心策略的定义

　　【定义1】 贪心策略是指从问题的初始状态出发，通过若干次的贪心选择而得出最优值(或较优解)的一种解题方法。

　　其实，从"贪心策略"一词我们便可以看出，贪心策略总是做出在当前看来是最优的选择，也就是说贪心策略并不是从整体上加以考虑，它所做出的选择只是在某种意义上的局部最优解，而许多问题自身的特性决定了该题运用贪心策略可以得到最优解或较优解。 

二、贪心算法的特点

　　通过上文的介绍，可能有人会问：贪心算法有什么样的特点呢？我认为，适用于贪心算法解决的问题应具有以下2个特点：

　　1、贪心选择性质：

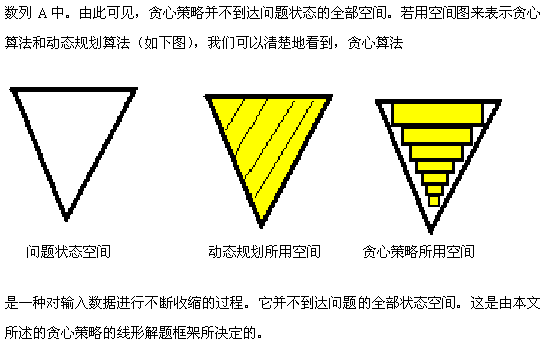
　　所谓贪心选择性质是指应用同一规则f，将原问题变为一个相似的、但规模更小的子问题、而后的每一步都是当前看似最佳的选择。这种选择依赖于已做出的选择，但不依赖于未做出的选择。从全局来看，运用贪心策略解决的问题在程序的运行过程中无回溯过程。关于贪心选择性质，读者可在后文给出的贪心策略状态空间图中得到深刻地体会。

　　2、局部最优解： 

　　我们通过特点2向大家介绍了贪心策略的数学描述。由于运用贪心策略解题在每一次都取得了最优解，但能够保证局部最优解得不一定是贪心算法。如大家所熟悉得动态规划算法就可以满足局部最优解，在广度优先搜索（BFS）中的解题过程亦可以满足局部最优解。

　　在遇到具体问题时，往往分不清哪些题该用贪心策略求解，哪些题该用动态规划法求解。在此，我们对两种解题策略进行比较。

         

     

     

三、 贪心策略的理论基础--矩阵胚 

正如前文所说的那样，贪心策略是最接近人类认知思维的一种解题策略。但是，越是显而易见的方法往往越难以证明。下面我们就来介绍贪心策略的理论--矩阵胚。
　　"矩阵胚"理论是一种能够确定贪心策略何时能够产生最优解的理论，虽然这套理论还很不完善，但在求解最优化问题时发挥着越来越重要的作用。

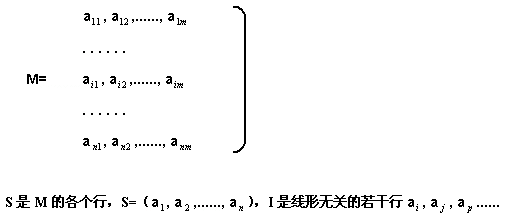
　　【定义[B]3】 矩阵胚是一个序对M=[S，I] ，其中S是一个有序非空集合，I是S的一个非空子集，成为S的一个独立子集。[/B]

　　如果M是一个N×M的矩阵的话，即:

若M是无向图G的矩阵胚的话，则S为图的边集，I是所有构成森林的一组边的子集。
　　如果对S的每一个元素X（X∈S）赋予一个正的权值W（X），则称矩阵胚M=（S，I）为一个加权矩阵胚。

　　适宜于用贪心策略来求解的许多问题都可以归结为在加权矩阵胚中找一个具有最大权值的独立子集的问题，即给定一个加权矩阵胚，M=（S，I），若能找出一个独立且具有最大可能权值的子集A，且A不被M中比它更大的独立子集所包含，那么A为最优子集，也是一个最大的独立子集。
　矩阵胚理论对于我们判断贪心策略是否适用于某一复杂问题是十分有效的。

四、  几种典型的贪心算法

   贪心策略在图论中有着极其重要的应用。诸如Kruskal、 Prim、 Dijkstra等体现“贪心”思想的图形算法更是广泛地应用于树与图的处理。下面就分别来介绍Kruskal算法、Prim算法和Dijkstra算法。

.

Ⅰ、库鲁斯卡尔（Kruskal）算法[B][/B]

【定义4】 设图G=（V，E）是一简单连通图，｜V｜ =n,｜E｜=m,每条边ei都给以权W ，W 假定是边e 的长度（其他的也可以），i=1，2，3，...，m。求图G的总长度最短的树，这就是最短树问题。

    kruskal算法的基本思想是：首先将赋权图G的边按权的升序排列，不失一般性为：e ,e ,......,e 。其中W ≤W ，然后在不构成回路的条件下择优取进权最小的边。

    其流程如下：

    （1） 对属于E的边进行排序得e ≤e ≤...... ≤e 。

    （2） 初始化操作  w←0，T←ф ，k←0，t←0；

    （3） 若t=n-1，则转（6），否则转（4）

    （4） 若T∪｛e ｝构成一回路，则作 

                 【k←k+1，转（4）】

    （5） T←T∪{ e }，w←w+ w ，t←t+1，k←k+1，转（3）

    （6） 输出T，w，停止。

     下面我们对这个算法的合理性进行证明。

设在最短树中，有边〈v ，v 〉，连接两顶点v ，v ，边〈v ，v 〉的权为wp，若〈v ，v 〉加入到树中不能保证树的总长度最短，那么一定有另一条边〈v ，v 〉或另两条边〈v ，v 〉、〈v ，v 〉，且w<vi，vj><wp或w<vi，vk>+w〈vk，vj〉<wp，因为〈v ，v 〉、〈v ，v 〉不在最短树中，可知当〈v ，v 〉、〈v ，v 〉加入到树中时已构成回路，此时程序终止。因为〈v ，v 〉∈ T，〈v ，v 〉∈T且w〈vI，vk〉+w〈vk，vj〉<w p，与程序流程矛盾。

下面给出C语言描述的kruskal算法:

#define MAXE <最多的边数>

typedef struct {

 int u;// 边的起始顶点 

 int v;// 边的终止顶点 

 int w;// 边的权值 

} Edge;

void kruskal(Edge E[],int n,int e)//边的权值从小到大排列  

{

    int i,j,m1,m2,sn1,sn2,k;

    int vset[MAXV];

    for(i=0;i<n;i++)

     vset[i]=i;

    k=1;j=0;

    while(k<n)

    {

        m1=E[j].u;

        m2=E[j].v;

        sn1=vset[m1];

        sn2=vset[m2];

        if(sn1!=sn2)//两顶点属于不同的集合,是最小生成树的一条边

         {

             输出这条边;

             k++;

             for(i=0;i<n;i++)

              if(vset[i]==sn2)

               vset[i]=sn1; 

         } 

        j++;     

    }     

} 

kruskal算法对边的稀疏图比较合适,时间复杂度为o(elog2e),e是边数,与顶点无关. 

Ⅱ、普林（Prim）算法：[B][/B]

   Kruskal算法采取在不构成回路的条件下，优先选择长度最短的边作为最短树的边，而Prim则是采取了另一种贪心策略。

    已知图G=（V，E），V={v ，v ，v ，...， v }，D=（d ） 是图G的矩阵，若〈v ，v 〉∈E，则令dij=∞，并假定dij=∞

    Prim算法的基本思想是：从某一顶点（设为v ）开始，令S←｛v ｝，求V/S中点与S中点v 距离最短的点，即从矩阵D的第一行元素中找到最小的元素，设为d ，则令S←S∪ { v }，继续求V/S中点与S的距离最短的点，设为v ,则令S←S∪{ v }，继续以上的步骤，直到n个顶点用n-1条边连接起来为止。

流程如下：

(1)     初始化操作：Ｔ←ф，ｑ（1）←-1，ｉ从２到ｎ作

【ｐ（ｉ）←1，ｑ（ｉ）←ｄｉ１】，ｋ←1

(2) 若ｋ≥n,则作【输出T,结束】

否则作【min←∞，ｊ从２到ｎ作

【若０<q(i)<min则作

【min←q(i) h←j】

　　　　　　　　　　】

　　　　　　　　】

(3) Ｔ←Ｔ∪{ｈ，p(h)},q(h)←-1

(4) ｊ从２到ｎ作

　　　　 【若d <q(j)则作【q(j)←d ,p(j)←h】】

(5) ｋ←ｋ＋１，转(2)

算法中数组p（i）是用以记录和v 点最接近的属于S的点，q（i）则是记录了v 点和S中点的最短距离，q（i）=-1用以表示v 点已进入集合S。算法中第四步：v 点进入S后，对不属于S中的点vj的p（j）和q（j）进行适当调整，使之分别记录了所有属于S且和S距离最短的点和最短的距离，点v , v ，…，v 分别用1，2，…,n表示。

下面给出C语言描述的prim算法:

 void prim(int cost[][MAXV],int n,int v)//v是起始顶点

{

    int lowcost[MAXV],min;

    int closest[MAXV],i,j,k;

 /*closest[i]表示U中的一个顶点,该顶点和V-U中的一个顶点构成的边(i,closese[i])具有最小的权 */

 //lowcost[i]表示边(i,closet[i])的权值 

  for(i=0;i<n;i++)

     {

         lowcost[i]=cost[v][i];

         closest[i]=v;

     } 

  for(i=1;i<n;i++)

  {

   min=INF;

   for(j=0;j<n;j++)//在(V-U)中找出离U最近的顶点K.

   if(lowcost[j]!=0&&lowcost[j]<min)

    {

      min=lowcost[j];

      k=j;   

    } 

   输出边: closet[k]-->k;

   lowcost[k]=0;//标记k已经加入U;

   for(j=0;j<n;j++)//修改数组lowcost和closest 

    if(cost[k][j]!=0&&cost[k][j]<lowcost[j])

     {

         lowcost[j]=cost[k][j];

         closest[j]=k;

     }           

  }          

}     

Prim算法的时间复杂度为O(n^2),与边无关,适用于边稠密的图[B][/B]

 

Ⅲ、戴克斯德拉（Dijkstra）算法：[B][/B]

给定一个（无向）图G，及G中的两点s、t，确定一条从s到t的最短路径。

a[i][j]记边（i,j）的权，数组dist[u]记从源v到顶点u所对应的最短特殊路径长度

       算法描述如下：

S1:初始化，S, T,对每个yS，{dist[y]=a[v][y],prev[y]=nil}

S2:若S=V，则输出dist,prev,结束

S3：uV/S中有最小dist值的点，SS{u}

S4：对u的每个相邻顶点x，调整dist[x]：即

若dist[x]>dist[u]+a[u][x],则{dist[x]=dist[u]+a[u][x]，prev[x]=u},转S2

 对于具有n个顶点和e条边的带权有向图，如果用带权邻接矩阵表示这个图，那么Dijkstra算法的主循环体需要O(n)时间。这个循环需要执行n-1次，所以完成循环需要O(n2)时间。算法的其余部分所需要时间不超过O(n2)。

五、贪心策略在P类问题求解中的应用   

在现实世界中，我们可以将问题分为两大类。其中一类被称为P类问题，它存在有效算法，可求得最优解；另一类问题被称为NPC类问题，这类问题到目前为止人们尚未找到求得最优解的有效算法，这就需要每一位程序设计人员根据自己对题目的理解设计出求较优解的方法。下面我们着重分析贪心策略在求解P类问题中的应用。

 

在现实生活中，P类问题是十分有限的，而NPC类问题则是普遍的、广泛的。

[例1]删数问题[B][/B]

试题描述  键盘输入一个高精度的正整数N(不超过240位)，去掉其中任意S个数字后剩下的数字按左右次序组成一个新的正整数。对给定的N和S，寻找一种删数规则使得剩下得数字组成的新数最小。

试题背景  此题出自NOI94[B][/B]

试题分析  这是一道运用贪心策略求解的典型问题。此题所需处理的数据从表面上看是一个整数。其实，大家通过对此题得深入分析便知：本题所给出的高精度正整数在具体做题时将它看作由若干个数字所组成的一串数，这是求解本题的一个重要突破。这样便建立起了贪心策略的数学描述。

每次删除一个数字,选择一个使剩下的数最小的数字作为删除对象,之所以选择这样”贪心”的操作,是因为删S个数字的全局最优解包含了删一个数字的子问题的最优解.

当S=1时,在N中删除哪一个数字能达到最小的目的?从左到右每相邻的两个数字比较:若出现左边大于右边,则删除左边的大数字.若不出现降序排列,即所有数字全部升序,则删除最右边的大数字.

当S>1,按上述操作一个一个删除,删除一个达到最小后,再从头即从串首开始,删除第2个,依次分解为S次完成.

若删除不到S个后已无左边大于右边的减序,则停止删除操作,打印剩下串的左边L-S个数字即可(相当于删除了若干个最右边的大数字,这里L为原数字N的位数).

附源程序:

#include<iostream>

#include<string>

using namespace std;

int main()

 {

   string n;

   int s,i,x,l,m;

   while(cin>>n>>s)

   {

        i=-1,m=0,x=0;

        l=n.length();  

        while(x<s&&m==0)

         {

             i++;

             if(n[i]>n[i+1])//出现递减,删除递减的首数字 

              {

                  n=n.erase(i,1);

                  x++;// x统计删除数字的个数 

                  i=-1;//从头开始查递减区间 

              } 

 

             if(i==l-x-2&&x<s)

             m=1;//已经无递减区间,m=1脱离循环 

         } 

     cout<<n.substr(0,l-s+x);//只打印剩下的左边l-(s-x)个数字 

 

   }    

 }    

[例2]数列极差问题[B][/B]

试题描述   在黑板上写了N个正整数作成的一个数列，进行如下操作：每一次擦去其中的两个数a和b，然后在数列中加入一个数a×b+1，如此下去直至黑板上剩下一个数，在所有按这种操作方式最后得到的数中，最大的max，最小的为min，则该数列的极差定义为M=max-min。

编程任务：对于给定的数列，编程计算出极差M。

试题分析  当看到此题时，我们会发现求max与求min是两个相似的过程。若我们把求解max与min的过程分开，着重探讨求max的问题。

　　下面我们以求max为例来讨论此题用贪心策略求解的合理性。

讨论：假设经（Ｎ－3）次变换后得到３个数：a,b,max＇

（max＇≥ａ≥ｂ），其中max＇是（Ｎ－２）个数经（Ｎ－３）次ｆ变换后所得的最大值，此时有两种求值方式，设其所求值分别为Ｚ ，Ｚ ，则有：Ｚ ＝（ａ×ｂ＋１）×max＇＋１，Ｚ ＝（ａ×max＇＋１）×ｂ+１　所以　Ｚ －Ｚ ＝max＇－ｂ≥０若经（Ｎ－２）次变换后所得的３个数为：ｍ，ａ，ｂ（ｍ≥ａ≥ｂ）且ｍ不为（Ｎ－２）次变换后的最大值，即ｍ＜max＇则此时所求得的最大值为：Ｚ ＝（ａ×ｂ+１）×ｍ+１　此时Ｚ －Ｚ ＝（１+ａｂ）（max＇－ｍ）＞０　所以此时不为最优解。

　　所以若使第ｋ（１≤ｋ≤Ｎ－１）次变换后所得值最大，必使（ｋ－１）次变换后所得值最大（符合贪心策略的特点2），在进行第ｋ次变换时，只需取在进行（ｋ－１）次变换后所得数列中的两最小数ｐ，ｑ施加ｆ操作：ｐ←ｐ×ｑ+1，ｑ←∞即可（符合贪心策略特点1），因此此题可用贪心策略求解。讨论完毕。

　　在求ｍｉｎ时，我们只需在每次变换的数列中找到两个最大数ｐ，ｑ施加作用ｆ：ｐ←ｐ×ｑ+１，ｑ←-∞即可．原理同上

[例３］最优乘车问题[B][/B]

试题描述　Ｈ城是一个旅游胜地，每年都有成千上万的人前来观光．为方便游客，巴士公司在各个旅游景点及宾馆、饭店等地都设置了巴士站，并开通了一些单向巴士线路。每条单向巴士线路从某个巴士站出发，依次途径若干个巴士站，最终到达终点巴士站。

　　阿昌最近到Ｈ城旅游，住在ＣＵＰ饭店。他很想去Ｓ公园游玩。听人说，从ＣＵＰ饭店到Ｓ公园可能有也可能没有直通巴士。如果没有，就要换乘不同线路的单向巴士，还有可能无法乘巴士到达。

　　现在用整数１，２，...，ｎ给Ｈ城的所有巴士站编号，约定ＣＵＰ饭店的巴士站编号为１，Ｓ公园巴士站的编号为Ｎ。

写一个程序，帮助阿昌寻找一个最优乘车方案，使他在从ＣＵＰ饭店到Ｓ公园的过程中换车的次数最少。

试题背景  出自ＮＯＩ９７

试题分析  此题看上去很像一道搜索问题。在搜索问题中，我们所求的使经过车站数最少的方案，而本题所求解的使换车次数最少的方案。这两种情况的解是否完全相同呢？我们来看一个实例：

 

如图5所示：共有５个车站（分别为ａ、ｂ、ｃ、ｄ、ｅ），　共有３条巴士线（线路Ａ：ａ→ｄ；线路Ｂ：ａ→ｂ→ｃ→ｅ；线路Ｃ：ｄ→ｅ）。此时要使换车次数最少，应乘坐线路Ｂ的巴士，路线为：ａ→ｂ→ｃ→ｅ，换车次数为０；要使途经车站数最少，乘坐线路应为ａ→ｄ→ｅ，换车次数为１。所以说使换车次数最少的路线和使途经车站数最少的方案不一定相同。这使不能用搜索发求解此问题的原因之一。

原因之二，来自对数学模型的分析。我们根据题中所给数据来建立一个图后会发现该图中存在大量的环，因而不适合用搜索法求解。

其实，此题完全可以套用上文所提到的Dijkstra算法来求解。

输入数据：输入文件INPUT.TXT。文件的第1行是一个数字M（1≤M≤100）表示开通了M条单向巴士线路，第2行是一个数字N（1<N≤500），表示共有N个车站。从第3行到第M+2行依次给出了第一条到第M条巴士线路的信息。其中第i+2行给出的是第i条巴士线路的信息，从左至右依次按行行驶顺序给出了该线路上的所有站点，相邻两个站号之间用一个空格隔开。 

　　输出数据：输出文件是OUTPUT.TXT。文件只有一行，为最少换车次数（在0，1，…，M-1中取值），0表示不需换车即可达到。如果无法乘车达到S公园，则输出"NO"。

源程序:

#include<iostream>

#include<cstdio>

#include<cstring>

using namespace std;

int m,n;         //m为开通的单向巴士线路数,n为车站总数

int result[502];   //到某车站的最少换车数

int num[502][52]; //从某车站可达的所有车站序列

int sum[502];    //从某车站可达的车站总数

bool check[502];  //某车站是否已扩展完

const int INF=600;

int main()

{   

 

     int i,j,c,a,b,d,min;

     int data[52];

     char ch;

     while(cin>>m>>n)

      {

 

      memset(sum,0,sizeof(sum));

      memset(num,0,sizeof(num));

          for(i=0;i<m;i++)

           {

               j=0;

               memset(data,0,sizeof(data));

               while(1)

                {

                    j++;

                    cin>>data[j];

                    ch=getchar();

                    if(ch!=' ')

                    break;

                }  

               for(c=1;c<=j-1;c++)

                for(d=c+1;d<=j;d++)

                {

                    sum[data[c]]++;

                    num[data[c]][sum[data[c]]]=data[d];

                }      

           }    

    memset(result,-1,sizeof(result));

    memset(check,0,sizeof(check));

    result[1]=0;

    for(c=1;c<=sum[1];c++)

     result[num[1][c]]=0;

    b=num[1][1];

    do

    {

        check[b]=1;//某车站已扩展完

        for(c=1;c<=sum[b];c++)

         if(result[num[b][c]]==-1)

          result[num[b][c]]=result[b]+1;

        min=501; result[min]=INF;

    /*贪心选择目前经过最小换乘数就可以到达的某车站 */    

        for(c=1;c<=n;c++)

         if(result[c]!=-1&&result[c]<result[min]&&check[c]==0)

          min=c; 

        b=min;   

    }while((result[n]==-1)&&(min!=501));//min=501表示目前所有车站已扩展完    

    if(result[n]==-1)//站点n无法到达 

     cout<<"NO"<<endl;

    else

     cout<<result[n]<<endl; 

 

    }

    return 0;

}    

［例４］最佳浏览路线问题[B][/B]

[试题描述]　某旅游区的街道成网格状（见图），其中东西向的街道都是旅游街，南北向的街道都是林荫道。由于游客众多，旅游街被规定为单行道。游客在旅游街上只能从西向东走，在林荫道上既可以由南向北走，也可以从北向南走。

　　阿隆想到这个旅游区游玩。他的好友阿福给了他一些建议，用分值表示所有旅游街相邻两个路口之间的道路值得浏览得程度，分值从-１００到１００的整数，所有林荫道不打分。所有分值不可能全是负值。

　　例如下图是被打过分的某旅游区的街道图：

阿隆可以从任一路口开始浏览，在任一路口结束浏览。请你写一个程序，帮助阿隆寻找一条最佳的浏览路线，使得这条路线的所有分值总和最大。

试题背景　　这道题同样出自ＮＯＩ９７，＇９７国际大学生程序设计竞赛的第二题（吉尔的又一个骑车问题）与本题是属于本质相同的题目。

试题分析  由于林荫道不打分，也就是说，无论游客在林荫道中怎么走，都不会影响得分。因题可知，若游客需经过某一列的旅游街，则他一定要经过这一列的Ｍ条旅游街中分值最大的一条，才会使他所经路线的总分值最大。这是一种贪心策略。贪心策略的目的是降维，使题目所给出的一个矩阵便为一个数列。下一步便是如何对这个数列进行处理。在这一步，很多人用动态规划法求解，这种算法的时间复杂度为Ｏ（ｎ ），当林荫道较多时，效率明显下降。其实在这一步我们同样可以采用贪心法求解。这时的时间复杂度为Ｏ（ｎ）。

输入数据：输入文件是INPUT.TXT。文件的第一行是两个整数M和N，之间用一个空格符隔开，M表示有多少条旅游街（1≤M≤100），N表示有多少条林荫道（1≤N≤20000）。接下里的M行依次给出了由北向南每条旅游街的分值信息。每行有N-1个整数，依次表示了自西向东旅游街每一小段的分值。同一行相邻两个数之间用一个空格隔开。 

　　输出文件：输出文件是 OUTPUT.TXT。文件只有一行，是一个整数，表示你的程序找到的最佳浏览路线的总分值。

源程序:

#include<iostream>

#include<cstring>

using namespace std;

int m,n;//m为旅游街数，n为林荫道数

int data[20000];//data是由相邻两条林荫道所分隔的旅游街的最大分值

int MaxSum(int n, int *a)//求最大子段和函数 

{

    int sum=0;

    int b=0;

    for(int i=1;i<=n;i++)

     {

         b+=a[i];

         if(b>sum) sum=b;

         if(b<0) b=0;

     }  

    return sum;   

}    

int main()

{

    int i,j,c;

    while(cin>>m>>n)

     {

         /*读取每一段旅游街的分值，并选择读取每一段旅游街的分值，

         并选择到目前位置所在列的最大分值记入数组data*/

         for(i=1;i<=n-1;i++)

          cin>>data[i];

         for(i=2;i<=m;i++)

          for(j=1;j<=n-1;j++)

           {

               cin>>c;

               if(c>data[j])

               data[j]=c;

           }     

     }  

    cout<<MaxSum(n-1,data)<<endl;   

    return 0;

}