热门标签
热门文章
- 1XAF应用开发教程(一) 创建项目
- 2TCP协议三次握手及四次挥手_第三次握手syn的值
- 3JSP和Servlet_jsp和servlet的区别jsp可读性强
- 4使用Bmob后端云实现的微信支付(后端处理),如何防止重复通知/多次回调_bmob 微信支付
- 5资深架构师亲授:Java开发中的那些坑,你避开了吗?
- 6AI赋能—EasyCVR视频融合平台为春节人员流动保驾护航_视频融合对摄像头的要求
- 7elementPlus自定义主题色_element plus 主题色
- 8怿星科技测试实验室(EPT LABS)服务介绍
- 9【实用工具介绍】0 PCAN-Explorer 5 安装及使用_用哪个软件分析pcan-explorer5保存的文件
- 10机器学习---普通线性回归模型
当前位置: article > 正文
【点云】生成有凹凸的平面
作者:不正经 | 2024-02-18 16:25:36
赞
踩
【点云】生成有凹凸的平面
前言
尝试用一些数据生成有凹凸面的点云。
我们姑且把z轴当成有凹凸的缺陷,x轴和y轴共同组成一个平面。
高斯函数
原理
高斯函数wiki中,我们得知

其中,σ为标准差,用来控制“钟形”的宽度。
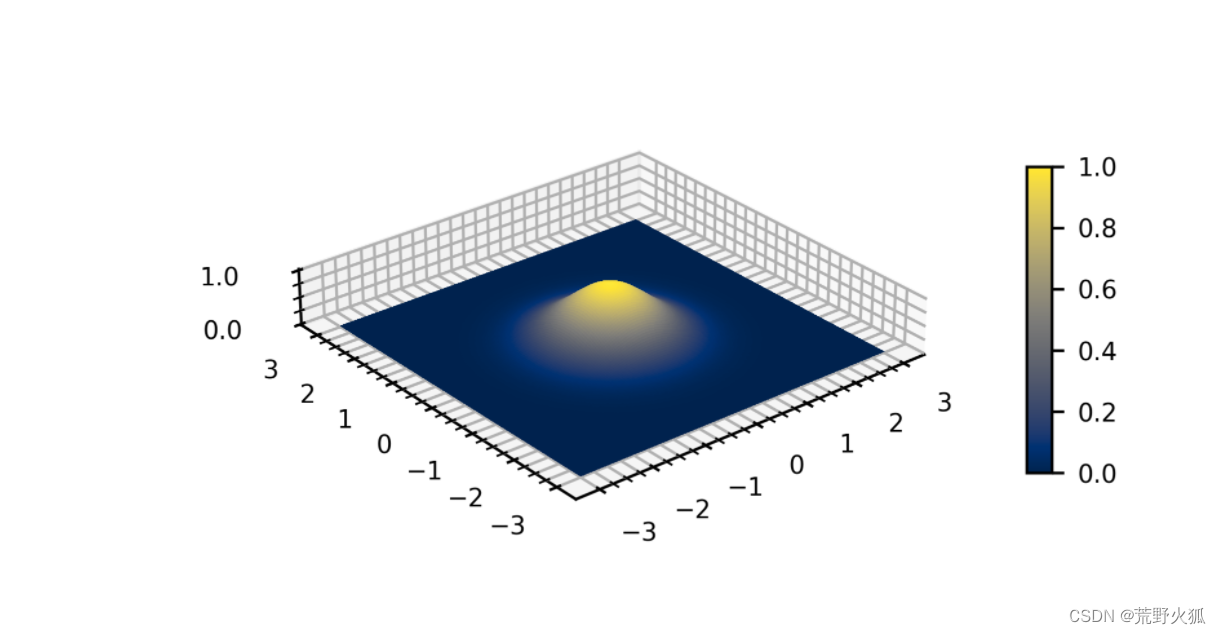
根据wiki中下面的举例sigma_X = 1;sigma_Y = 2;可以看出,σx=σy时,高斯的水平集是个圆,σx不等于σy时,高斯的水平集是个椭圆。(可以这样想:在平面上的公式,圆和椭圆的区别)
继续往下看:
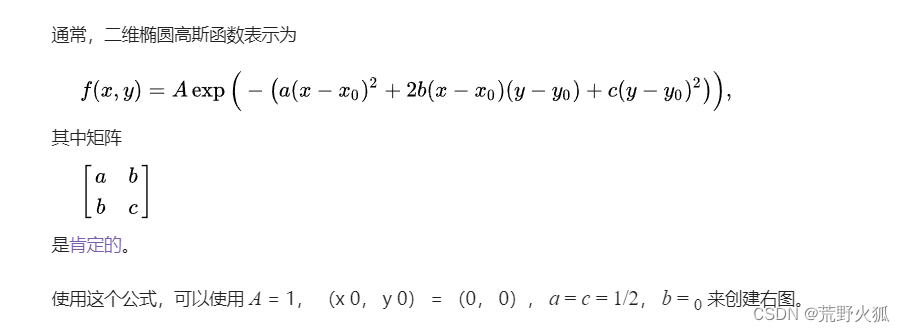

代码
再根据wiki中下面的 Octave 代码,仿写出python代码:
# 导入 numpy 和 open3d 库 import numpy as np import open3d as o3d # 定义高斯函数的参数 A = 1 x0 = 0 y0 = 0 sigma_X = 1 sigma_Y = 2 # 生成 X 和 Y 的坐标网格 X, Y = np.meshgrid(np.arange(-5, 5.1, 0.1), np.arange(-5, 5.1, 0.1))#-5到5,步长为0.1 # 创建 open3d 点云对象 pcd = o3d.geometry.PointCloud() # 循环旋转角度 for theta in np.arange(0, np.pi, np.pi / 100): # 0 到 π,步长为 π / 100 #可以改变这个值 # 计算高斯函数的系数 a = np.cos(theta) ** 2 / (2 * sigma_X ** 2) + np.sin(theta) ** 2 / (2 * sigma_Y ** 2) b = np.sin(2 * theta) / (4 * sigma_X ** 2) - np.sin(2 * theta) / (4 * sigma_Y ** 2) c = np.sin(theta) ** 2 / (2 * sigma_X ** 2) + np.cos(theta) ** 2 / (2 * sigma_Y ** 2) # 计算 Z 的坐标 Z = A * np.exp(-(a * (X - x0) ** 2 + 2 * b * (X - x0) * (Y - y0) + c * (Y - y0) ** 2)) # 将 X, Y, Z 合并为点云矩阵,形状为 (n, 3) points = np.stack((X, Y, Z), axis=-1) points = points.reshape(-1, 3) # 更新点云的坐标 pcd.points = o3d.utility.Vector3dVector(points) # 添加坐标 coord = o3d.geometry.TriangleMesh.create_coordinate_frame(size=1, origin=[0, 0, 0])#x红色,y绿色,z蓝色 # 可视化点云 o3d.visualization.draw_geometries([pcd, coord])
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
得到
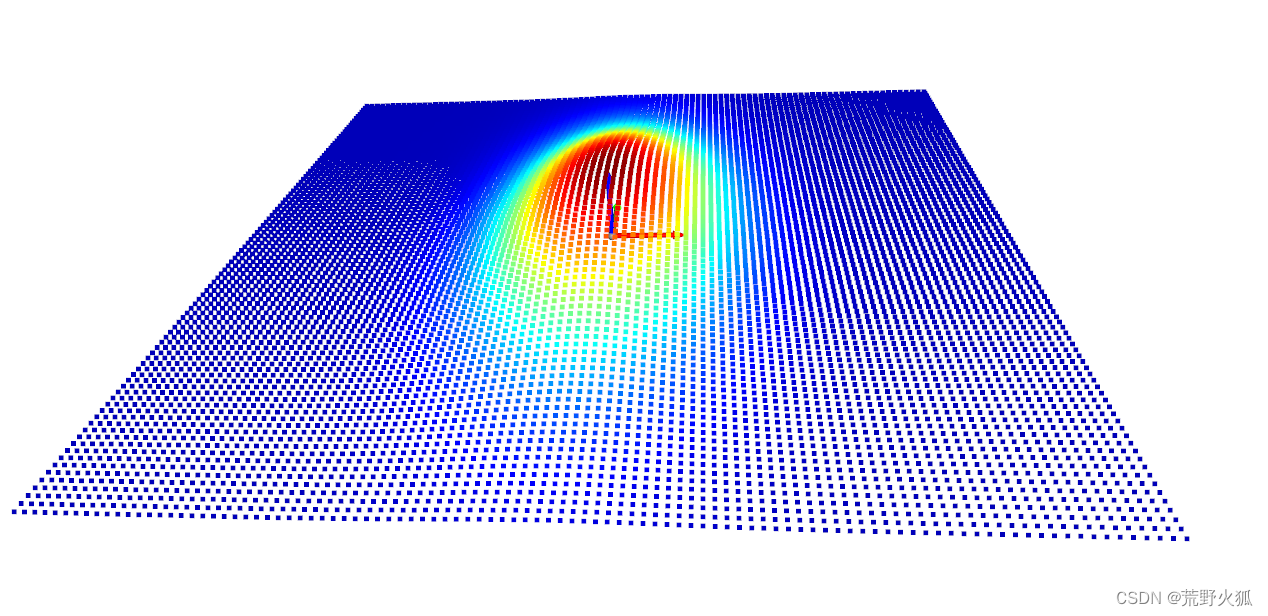
若我们改为sigma_X = 1,sigma_Y = 1,则
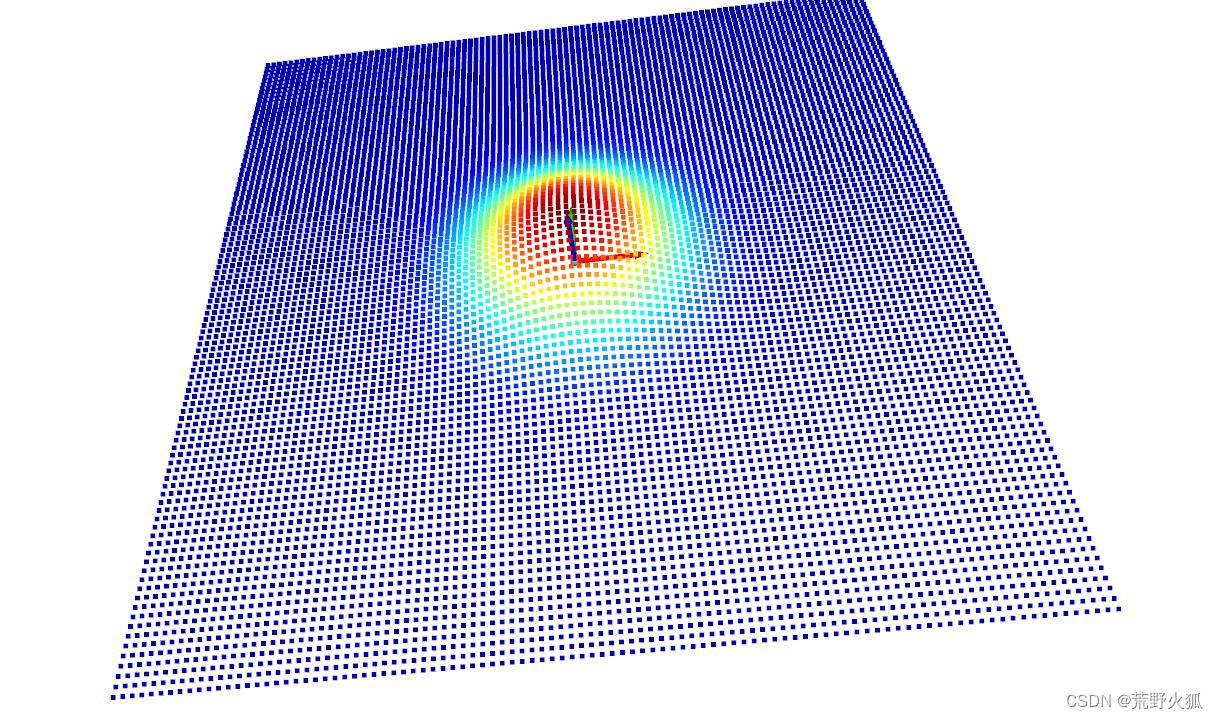
发现中间确实为圆,与上述猜想一致。
若我们需要凹陷的缺陷,则改为A=-1即可。

保存
# 保存点云
o3d.io.write_point_cloud("flaw.pcd",pcd )
- 1
- 2
点云大小如下:
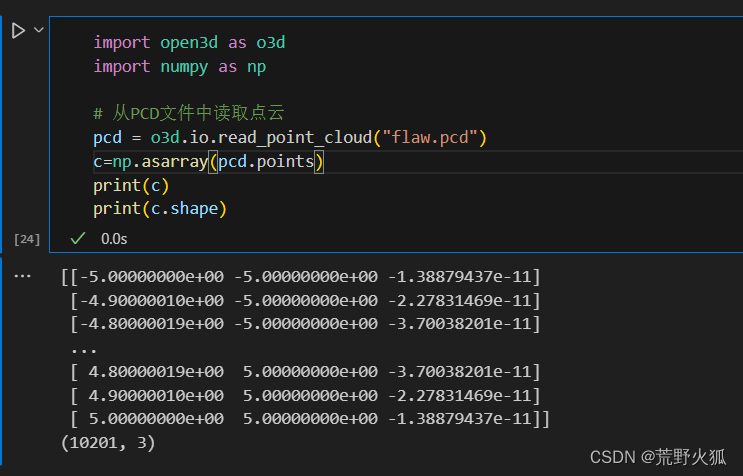
测试
【最详解】如何进行点云的凹凸缺陷检测(opene3D)
拿出之前写的凹凸检测代码开始测试,首先测试上述这种无噪音的。
记得一定要根据点云的大小改radius = 0.5 #邻域半径,否则一点效果也没有
测试1 :领域曲率代码
参数如下:
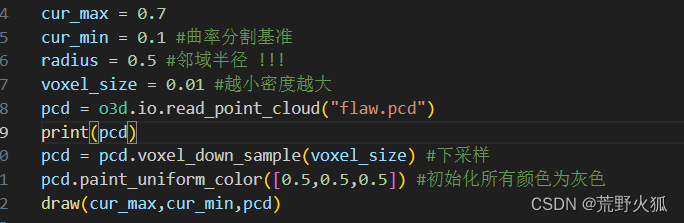
结果如下:

意外的还算不错。
测试2:高斯曲率代码
也是改了radius =0.5。

果然结果还是这个更好。
加上噪点
在之前代码的基础上更改如下,并改成椭圆形缺陷。
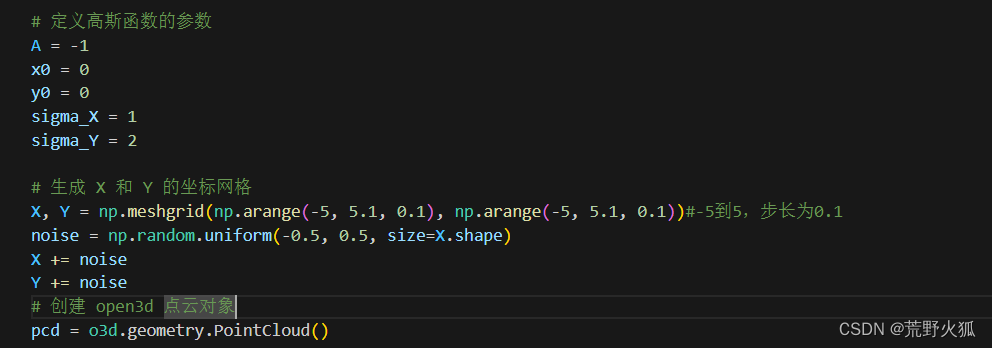
结果:
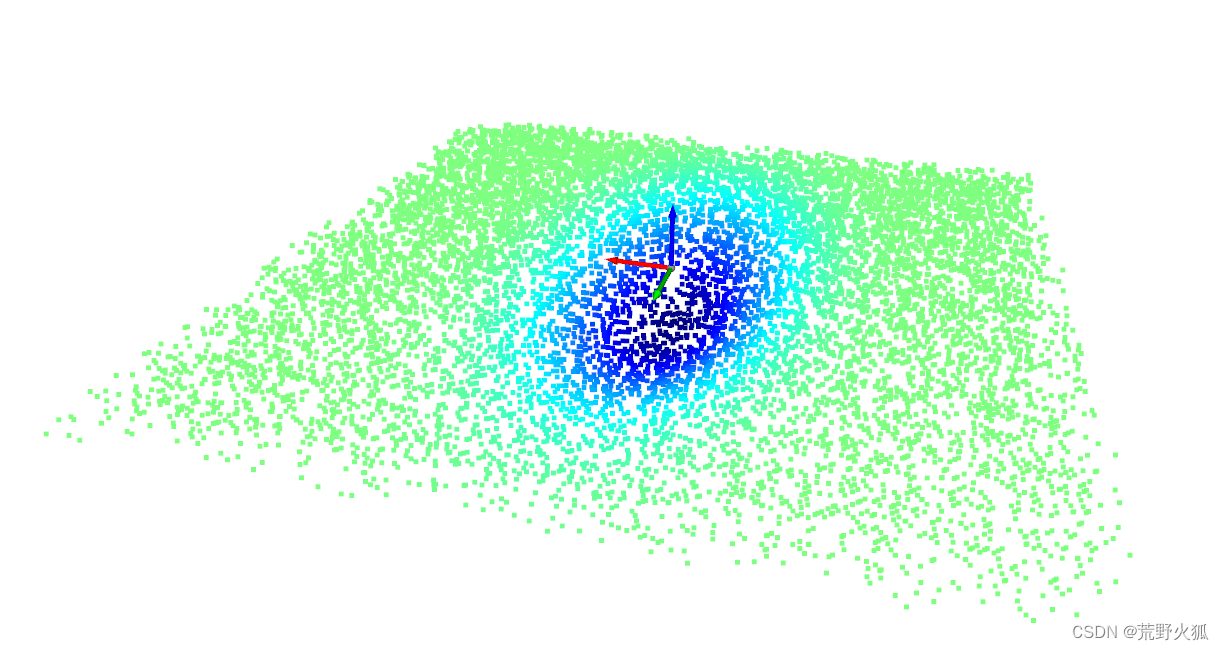
测试1
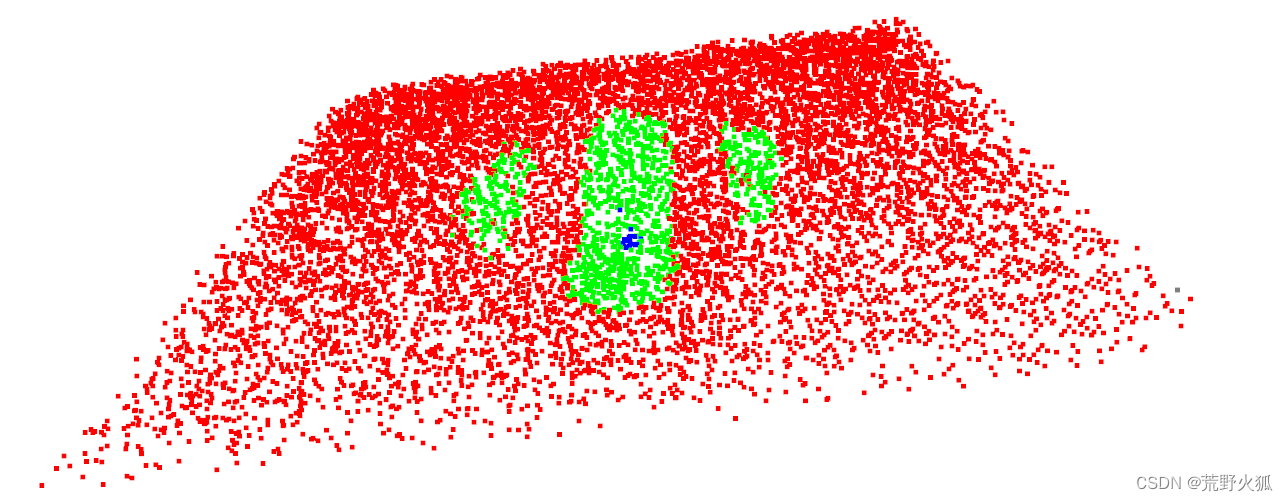
测试2

发现在针对椭圆形的凹凸缺陷都不够灵敏了。
改进
一开始以为在使用邻近搜索中,用的方法不太好,用的是在球内的点搜索,或许换个方法就可以了。–2024.2.17
后发现修改为如下,依旧不太好。
k, idx, _ = kdtree.search_knn_vector_3d(cloud.points[i], num_knn)
- 1
后发现在打印出数据中,数据太小,而定义为平面的数据宽泛太大,于是在测试2中改为如下
limit_max = 1e-3 for i in range(len(curvatures)): if -limit_max<curvatures[i][0] < limit_max and -limit_max<curvatures[i][1] <limit_max: #平坦 np.asarray(pcd.colors)[i] = [0, 0, 0]#黑 elif -limit_max<curvatures[i][0] < limit_max and curvatures[i][1] >limit_max: #凸 np.asarray(pcd.colors)[i] = [1, 0, 0]#红 elif -limit_max<curvatures[i][0] < limit_max and -limit_max<curvatures[i][1] <limit_max: #凹 np.asarray(pcd.colors)[i] = [0, 1, 0]#绿 elif curvatures[i][0] < -limit_max and curvatures[i][1] >limit_max: #鞍形脊 大部分凸,少部分凹 np.asarray(pcd.colors)[i] = [0, 0, 1]#蓝 elif curvatures[i][0] < -limit_max and curvatures[i][1] <-limit_max: #鞍形谷 大部分凹,少部分凸 np.asarray(pcd.colors)[i] = [0, 1, 1]#青 elif curvatures[i][0] > limit_max and curvatures[i][1] >limit_max: #峰 np.asarray(pcd.colors)[i] = [1, 0, 1]#紫 elif curvatures[i][0] > limit_max and curvatures[i][1] <-limit_max: #阱 np.asarray(pcd.colors)[i] = [1, 1, 0]#黄
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
结果便好很多了。
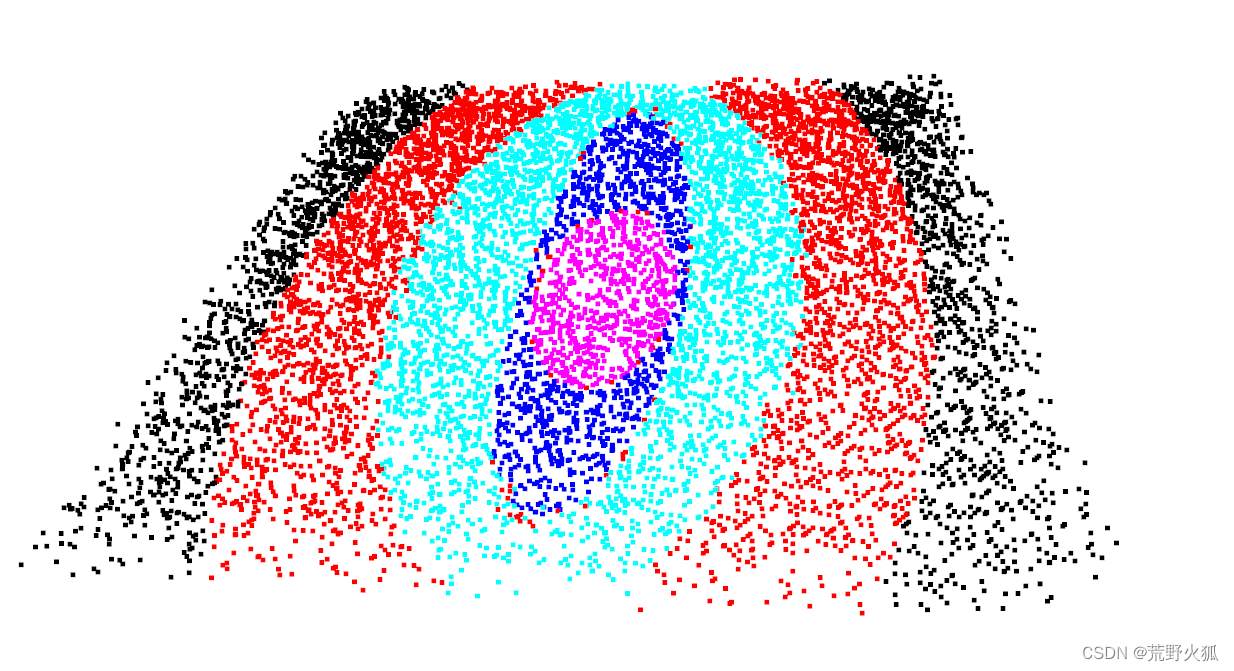
声明:本文内容由网友自发贡献,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:【wpsshop博客】
推荐阅读
相关标签



