【LeetCode】动态规划 刷题训练(四)

面试题 17.16. 按摩师(打家劫舍|)

点击查看：按摩师

---

一个有名的按摩师会收到源源不断的预约请求，每个预约都可以选择接或不接。在每次预约服务之间要有休息时间，因此她不能接受相邻的预约。给定一个预约请求序列，替按摩师找到最优的预约集合（总预约时间最长），返回总的分钟数。

示例 1：
输入： [1,2,3,1]
输出： 4
解释： 选择 1 号预约和 3 号预约，总时长 = 1 + 3 = 4。
示例 2：
输入： [2,7,9,3,1]
输出： 12
解释： 选择 1 号预约、 3 号预约和 5 号预约，总时长 = 2 + 9 + 1 = 12。

---

题目解析

从第一个数1开始，相邻的数不能够放在一起，所以再次 选择 3
即 1+3 =4
从第二个数2开始，相邻的数不能够放在一起，所以再次 选择 1
即 2+1 =3
所以 4 作为最长预约时长

状态转移方程

在上述分析过程中发现，是从左往右的

dp[i] ：表示 选到i位置的时候，此时的最长预约时长

---

对于i位置有两种情况：

1. 选择i 位置的值，选择用f 表示
f[i]：表示 选择i位置的时候，i位置的值(nums[i]) 必选，此时的最长预约时长

2. 不选 i位置的值，不选用g表示
g[i]：表示 选择i位置的时候，i位置的值(nums[i]) 不选， 此时的最长预约时长

---

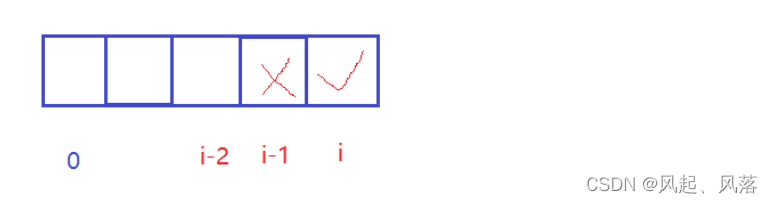
f[i]表示 i位置必定选择，则i-1位置必定不能被选
因为要的是最长预约时长，所以寻找[0，i-1] 区间内的最长预约时长 ，而i-1位置不能够被取到 即g[i-1]
再加上i位置的值 为 [0,i]区间的最长预约时长

状态转移方程 为：
f[i] = g[i-1]+nums[i]

---

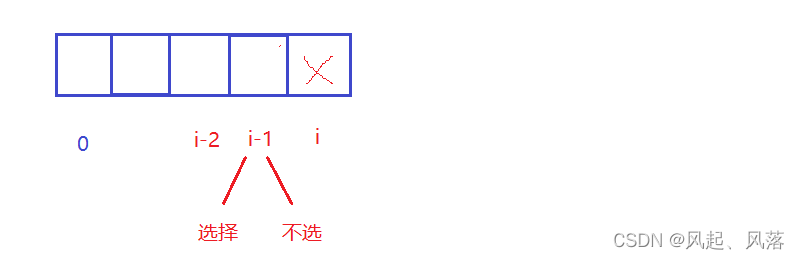
g[i] 表示 i位置必定不选，则i-1位置分为两种情况
第一种情况，i-1位置被选择
因为要的是最长预约时长，所以寻找[0，i-1] 区间内的最长预约时长 ，而i-1位置能够被取到 即f[i-1]
第一种情况下的最长预约时长为 ： g[i]=f[i-1]

第二种情况，i-1位置不选
因为要的是最长预约时长，所以寻找[0，i-1] 区间内的最长预约时长 ，而i-1位置不能够被取到 即g[i-1]
第二种情况下的最长预约时长为 ： g[i]=g[i-1]

状态转移方程为：
g[i] =max(f[i-1],g[i-1]);

---

完整代码

class Solution {
public:
    int massage(vector<int>& nums) {
       int n=nums.size();

       //处理边界条件
       if(n==0)
       {
           return 0;
       }
       vector<int>f(n,0);
       vector<int>g(n,0);
       int i=0;

       //为了防止越界问题 g[0]和f[0]都需要提前赋值
       g[0]=0;
       f[0]=nums[0];
       for(i=1;i<n;i++)
       {
          f[i]=g[i-1]+nums[i];
          g[i]=max(f[i-1],g[i-1]);
       }
       //返回 取到最后一个位置和 不取最后一个位置 两者的最大值
       return max(f[n-1],g[n-1]);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

i从1开始，所以要初始化f[0]和g[0]
f[0]包含nums[0]位置的值，所以为nums第一个元素
g[0]不包含nums[0]位置的值，所以为0

返回值为 到最后一个位置选 和到最后一个位置不选，两者中的最大值

213. 打家劫舍 II

点击查看：打家劫舍 II

---

你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组，计算你 在不触动警报装置的情况下 ，今晚能够偷窃到的最高金

示例 1：
输入：nums = [2,3,2]
输出：3
解释：你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。
示例 2：
输入：nums = [1,2,3,1]
输出：4
解释：你可以先偷窃 1 号房屋（金额 = 1），然后偷窃 3 号房屋（金额 = 3）。
偷窃到的最高金额 = 1 + 3 = 4 。

题目解析

相当于 打家劫舍| 不同点在于 首尾是相连的

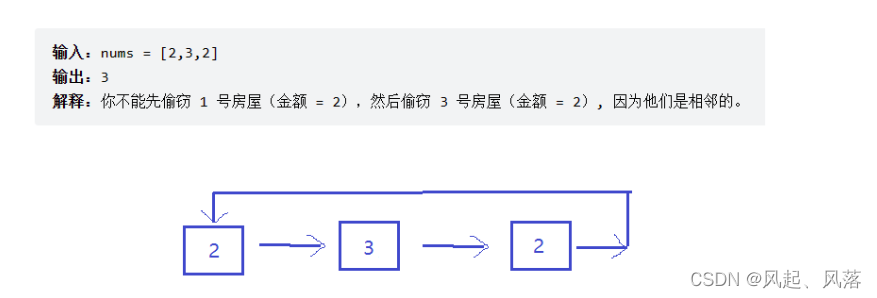
若取第一个节点中的值 2 ，则不能取第三个节点中的值 2 ，因为收尾相连 ，所以此时 能够偷取的金额为2

若 取 第二个节点中的值 3 ，则能够偷取的金额为3
所以 最大偷取金额 为 3

通过分类讨论，将环形问题，转换为两个线性的打家劫舍|

---

情况一：

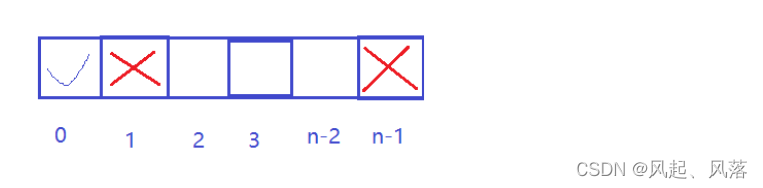
若偷取下标为0 的位置，因为首尾相连，所以下标为1的 位置 和 下标为n-1的位置就不能偷取到了
而在[2,n-2]区间内 随便偷取（用动态转移方程)

---

情况二：

若 不偷取 下标为0的位置，此时[1,n-1]区间内可以随便偷取（用动态转移方程)

取 两种情况下的最大值 即为 最大金额

状态转移方程

该动态转移方程 是用于上述分析的情况1中[2,n-2]区间内 随便偷取 和情况2中[1,n-1]区间内可以随便偷取的 情况

---

f[i]：表示偷取到i位置时，偷nums[i]，此时的最大金额
g[i]：表示偷取到i位置时，不偷nums[i]，此时的最大金额

---

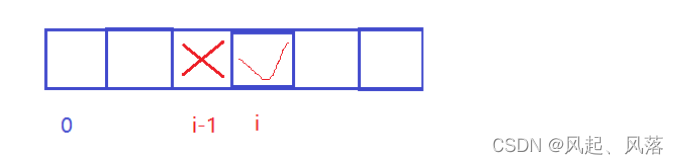
若i位置被偷取到 nums[i]的值，则想要求[0,i]的最大金额，就要先求[0,i-1]的最大金额
而由于相邻位置不能偷取，所以i-1位置不能偷取，即g[i-1]
再加上nums[i]的值 为为 [0,i]区间的最大金额

状态转移方程 为：
f[i]=g[i-1]+nums[i]

---

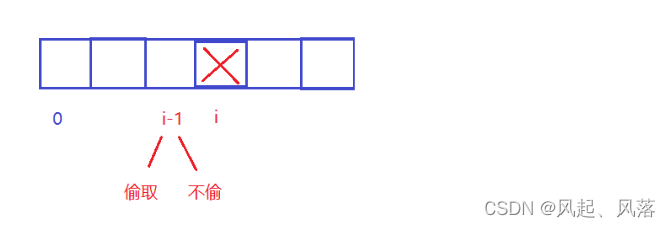
若i位置没有被偷取到 nums[i]的值，则i-1位置分为两种情况：

情况一：
若i-1位置的值被偷取，
因为要的是最大金额，所以寻找[0，i-1] 区间内的最长金额 ，而i-1位置能够被取到 即f[i-1]
第一种情况下的最大金额为 ： g[i]=f[i-1]

情况二：
若i-1位置的值没有被偷取，
因为要的是最大金额，所以寻找[0，i-1] 区间内的最大金额 ，而i-1位置不能够被取到 即g[i-1]
第二种情况下的最长最大金额为 ： g[i]=g[i-1]

状态转移方程 为：
g[i]=max(f[i-1],g[i-1]);

完整代码

class Solution {
public:
    int rob1(vector<int> &nums,int left,int right)
    {
        //区间不存在
        if(left>right)
        {
            return 0;
        }
        int n=nums.size();
        vector<int>f(n,0);
        vector<int>g(n,0);
        int i=0;
        //为了防止越界问题，所以下标left处要提前赋值
        f[left]=nums[left];
        g[left]=0;
        for(i=left;i<=right;i++)
        {
            f[i]=g[i-1]+nums[i];
            g[i]=max(f[i-1],g[i-1]);
        }
        //求 取到最后一个位置 和 没有取到最后一个位置 两者的最大值
        return max(f[right],g[right]);
    }
    int rob(vector<int>& nums) {
        int n=nums.size();
        //第一个位置取到值 和 第一个位置没有取到值 的两种情况
       return max(nums[0]+rob1(nums,2,n-2),rob1(nums,1,n-1));
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

n的取值为1到100，若n为1时，n-2为-1,就会导致下标left(1) 小于下标right(2) ，区间不存在

调用rob1，就在区间[left,right]内随便偷取，就相当于打家劫舍|的代码在调用

740. 删除并获得点数

点击查看：删除并获得点数

---

给你一个整数数组 nums ，你可以对它进行一些操作。
每次操作中，选择任意一个 nums[i] ，删除它并获得 nums[i] 的点数。之后，你必须删除 所有 等于 nums[i] - 1 和 nums[i] + 1 的元素。
开始你拥有 0 个点数。返回你能通过这些操作获得的最大点数。

示例 1：
输入：nums = [3,4,2]
输出：6
解释：
删除 4 获得 4 个点数，因此 3 也被删除。
之后，删除 2 获得 2 个点数。总共获得 6 个点数。
示例 2：
输入：nums = [2,2,3,3,3,4]
输出：9
解释：
删除 3 获得 3 个点数，接着要删除两个 2 和 4 。
之后，再次删除 3 获得 3 个点数，再次删除 3 获得 3 个点数。
总共获得 9 个点数。

题目解析

删除一个3，并获取3个点数，同时所有的2和4也被删除，依次删除3，并获取对应的点数
共获取 9个点数

预处理

若储存的数都是连续的，则相当于打家劫舍问题(不能选择两个相邻的数)
如：若选取 1 ，则不能选取2

---

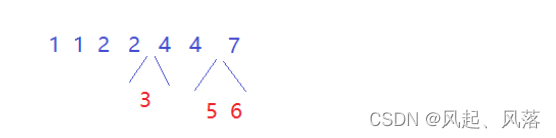
但是像这种不连续的数 ，缺少数字3和5 6，就没办法使用 类似打家劫舍问题的解决方法

---

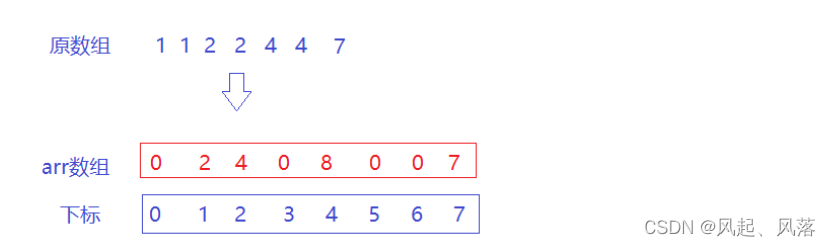
借助下标表示 对应的数，如：下标为1，表示为1的数
arr[i] ：表示 i 这个数，出现的总和
此时的下标就是连续的，就可以借助 打家劫舍问题的解决方法
如：若选取下标为1的数，则就不能选取下标为2的数，只能选择下标为3的数或者 下标为4的数

将原数组中数统计到 arr数组中，在arr数组中进行 打家劫舍

状态转移方程

以下就是 打家劫舍问题的状态转移方程(就是把原数组变为了arr数组，其他都是一样的)

---

对于i位置有两种情况：
1. 选择i 位置的值，选择用f 表示
f[i]：表示 选择i位置的时候，i位置的值(arr[i]) 必选，此时的最大点数

2. 不选 i位置的值，不选用g表示
g[i]：表示 选择i位置的时候，i位置的值(arr[i]) 不选， 此时的最大点数

---

f[i]表示 i位置必定选择，则i-1位置必定不能被选
因为要的是最大点数，所以寻找[0，i-1] 区间内的最大点数 ，而i-1位置不能够被取到 即g[i-1]
再加上i位置的值 为 [0,i]区间的最大点数

状态转移方程 为：
f[i] = g[i-1]+arr[i]

---

g[i] 表示 i位置必定不选，则i-1位置分为两种情况
第一种情况，i-1位置被选择
因为要的是最大点数，所以寻找[0，i-1] 区间内的最大点数 ，而i-1位置能够被取到 即f[i-1]
第一种情况下的最大点数为 ： g[i]=f[i-1]

第二种情况，i-1位置不选
因为要的是最大点数，所以寻找[0，i-1] 区间内的最大点数 ，而i-1位置不能够被取到 即g[i-1]
第二种情况下的最大点数为 ： g[i]=g[i-1]

状态转移方程为：
g[i] =max(f[i-1],g[i-1]);

完整代码

class Solution {
public:
    int deleteAndEarn(vector<int>& nums) {
         int i=0;
         int maxsize=0;
         //因为arr数组下标最大值为原数组的最大值 所以寻找原数组的最大值
         for(i=0;i<nums.size();i++)
         {
            if(nums[i]>maxsize)
            {
                maxsize=nums[i];
            }
         }
         //通过原数组的最大值创建arr数组大小
         vector<int>arr(maxsize+1,0);
         for(i=0;i<nums.size();i++)
         {
             //arr[i]代表 i这个数的总和
             arr[nums[i]]+=nums[i];
         }
         //下面进行 打家劫舍问题
        int n=arr.size();
        //[i]f代表取arr[i]这个位置的时候，能够得到的最大点数
        //g[i]代表不能取arr[i]这个位置的时候，能够得到的最大点数
         vector<int>g(n,0);
         vector<int>f(n,0);
         //为了避免越界 将g[0] f[0]进行初始化
         g[0]=0;
         f[0]=arr[0];
         for(i=1;i<n;i++)
         {
             //状态转移方程
             f[i]=g[i-1]+arr[i];
             g[i]=max(g[i-1],f[i-1]);
         }
         //返回 取到最后一个位置 和 不取最后一个位置 两者中的最大值
         return max(f[n-1],g[n-1]);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39