devbox
不正经
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

力扣OJ（6x）LCS、面试题_力扣面试题

作者：不正经 | 2024-04-26 04:10:02

赞

踩

力扣面试题

目录

LCS 01. 下载插件

LCS 02. 完成一半题目

LCS 03. 主题空间

面试题 01.01. 判定字符是否唯一

面试题 01.02. 判定是否互为字符重排

面试题 01.03. URL化

面试题 01.04. 回文排列

面试题 01.05. 一次编辑

面试题 01.06. 字符串压缩

面试题 01.07. 旋转矩阵

面试题 01.08. 零矩阵

面试题 01.09. 字符串轮转

面试题 02.01. 移除重复节点

面试题 02.02. 返回倒数第 k 个节点

面试题 02.03. 删除中间节点

面试题 02.04. 分割链表

面试题 02.05. 链表求和

面试题 02.06. 回文链表

面试题 02.07. 链表相交

面试题 02.08. 环路检测

面试题 03.02. 栈的最小值

面试题 04.01. 节点间通路

面试题 04.02. 最小高度树

面试题 04.03. 特定深度节点链表

面试题 04.04. 检查平衡性

面试题 04.05. 合法二叉搜索树

面试题 04.06. 后继者

面试题 04.08. 首个共同祖先

面试题 05.03. 翻转数位

面试题 05.04. 下一个数

面试题 05.06. 整数转换

面试题 05.08. 绘制直线

面试题 08.01. 三步问题

面试题 08.04. 幂集

面试题 08.06. 汉诺塔问题

面试题 08.11. 硬币

面试题 08.12. 八皇后

面试题 08.14. 布尔运算

面试题 10.01. 合并排序的数组

面试题 10.03. 搜索旋转数组

面试题 16.03. 交点

面试题 16.04. 井字游戏

面试题 16.05. 阶乘尾数

面试题 16.06. 最小差

面试题 16.07. 最大数值

面试题 16.16. 部分排序

面试题 16.17. 连续数列

面试题 16.19. 水域大小

面试题 16.20. T9键盘

面试题 16.21. 交换和

面试题 16.22. 兰顿蚂蚁

面试题 16.25. LRU 缓存

面试题 17.01. 不用加号的加法

面试题 17.04. 消失的数字

面试题 17.05. 字母与数字

面试题 17.06. 2出现的次数

面试题 17.07. 婴儿名字

面试题 17.09. 第 k 个数

面试题 17.12. BiNode

面试题 17.14. 最小K个数

面试题 17.17. 多次搜索

面试题 17.19. 消失的两个数字

面试题 17.20. 连续中值

面试题 17.21. 直方图的水量

面试题 17.26. 稀疏相似度

LCS 01. 下载插件

小扣打算给自己的 VS code 安装使用插件，初始状态下带宽每分钟可以完成 1 个插件的下载。假定每分钟选择以下两种策略之一:

  • 使用当前带宽下载插件
  • 将带宽加倍（下载插件数量随之加倍）

请返回小扣完成下载 n 个插件最少需要多少分钟。

注意：实际的下载的插件数量可以超过 n 个

示例 1：

输入：n = 2

输出：2

解释： 以下两个方案，都能实现 2 分钟内下载 2 个插件

  • 方案一：第一分钟带宽加倍，带宽可每分钟下载 2 个插件；第二分钟下载 2 个插件
  • 方案二：第一分钟下载 1 个插件，第二分钟下载 1 个插件

示例 2：

输入：n = 4

输出：3

解释： 最少需要 3 分钟可完成 4 个插件的下载，以下是其中一种方案: 第一分钟带宽加倍，带宽可每分钟下载 2 个插件; 第二分钟下载 2 个插件; 第三分钟下载 2 个插件。

提示：

  • 1 <= n <= 10^5
  1. class Solution {
  2. public:
  3.     int leastMinutes(int n) {
  4.         int ans = n, r=1,k=0;
  5.         while(r<n){
  6.             r*=2,k+=1,ans=min(ans,(n+r-1)/r+k);
  7.         }
  8.         return ans;
  9.     }
  10. };

LCS 02. 完成一半题目

有 N 位扣友参加了微软与力扣举办了「以扣会友」线下活动。主办方提供了 2*N 道题目，整型数组 questions 中每个数字对应了每道题目所涉及的知识点类型。 若每位扣友选择不同的一题，请返回被选的 N 道题目至少包含多少种知识点类型。

示例 1：

输入：questions = [2,1,6,2]

输出：1

解释：有 2 位扣友在 4 道题目中选择 2 题。 可选择完成知识点类型为 2 的题目时，此时仅一种知识点类型 因此至少包含 1 种知识点类型。

示例 2：

输入：questions = [1,5,1,3,4,5,2,5,3,3,8,6]

输出：2

解释：有 6 位扣友在 12 道题目中选择题目，需要选择 6 题。 选择完成知识点类型为 3、5 的题目，因此至少包含 2 种知识点类型。

提示：

  • questions.length == 2*n
  • 2 <= questions.length <= 10^5
  • 1 <= questions[i] <= 1000
  1. class Solution {
  2. public:
  3. 	int halfQuestions(vector<int>& questions) {
  4. 		map<int, int>m;
  5. 		for (auto x : questions)m[x]++;
  6. 		vector<int>v;
  7. 		for (auto mi : m)v.push_back(mi.second);
  8. 		sort(v.begin(), v.end());
  9. 		int s = 0;
  10. 		for (int i = v.size() - 1; i >= 0; i--) {
  11. 			s += v[i];
  12. 			if (s >= questions.size() / 2)return v.size() - i;
  13. 		}
  14. 		return -1;
  15. 	}
  16. };

LCS 03. 主题空间

并查集

面试题 01.01. 判定字符是否唯一

实现一个算法，确定一个字符串 s 的所有字符是否全都不同。

示例 1：

输入: s = "leetcode"
输出: false 
示例 2：

输入: s = "abc"
输出: true
限制：

0 <= len(s) <= 100
如果你不使用额外的数据结构，会很加分。

  1. class Solution:
  2.     def isUnique(self, s: str) -> bool:
  3.         s=sorted(s)
  4.         for i in range(1,len(s)):
  5.             if s[i]==s[i-1]:
  6.                 return False
  7.         return True

面试题 01.02. 判定是否互为字符重排

给定两个字符串 s1 和 s2，请编写一个程序，确定其中一个字符串的字符重新排列后，能否变成另一个字符串。

示例 1：

输入: s1 = "abc", s2 = "bca"
输出: true 
示例 2：

输入: s1 = "abc", s2 = "bad"
输出: false
说明：

0 <= len(s1) <= 100
0 <= len(s2) <= 100

  1. class Solution:
  2.     def CheckPermutation(self, s1: str, s2: str) -> bool:
  3.         s1=sorted(s1)
  4.         s2=sorted(s2)
  5.         return s1==s2

面试题 01.03. URL化

URL化。编写一种方法，将字符串中的空格全部替换为%20。假定该字符串尾部有足够的空间存放新增字符，并且知道字符串的“真实”长度。（注：用Java实现的话，请使用字符数组实现，以便直接在数组上操作。）

示例 1：

输入："Mr John Smith    ", 13
输出："Mr%20John%20Smith"
示例 2：

输入："               ", 5
输出："%20%20%20%20%20"
 

提示：

字符串长度在 [0, 500000] 范围内。

  1. class Solution:
  2.     def replaceSpaces(self, s: str, length: int) -> str:
  3.         ans=''
  4.         for i in range(len(s)):
  5.             if i>=length:
  6.                 break
  7.             if s[i]==' ':
  8.                 ans+='%20'
  9.             else:
  10.                 ans+=s[i]
  11.         return ans

面试题 01.04. 回文排列

rust

面试题 01.05. 一次编辑

字符串有三种编辑操作:插入一个英文字符、删除一个英文字符或者替换一个英文字符。 给定两个字符串，编写一个函数判定它们是否只需要一次(或者零次)编辑。

示例 1:

输入: 
first = "pale"
second = "ple"
输出: True

示例 2:

输入: 
first = "pales"
second = "pal"
输出: False
  1. class Solution {
  2. public:
  3.     bool oneEditAway(string first, string second) {
  4.         int d=int(first.length())-int(second.length());
  5.         if(d==0)return change(first,second);
  6.         if(d==1)return add(first,second);
  7.         if(d==-1)return add(second,first);
  8.         return false;
  9.     }
  10.     bool add(string first, string second) {
  11.         for(int i=0;i<second.length();i++){
  12.             if(first[i]==second[i])continue;
  13.             for(int j=i;j<second.length();j++){
  14.                 if(first[j+1]!=second[j])return false;
  15.             }
  16.             return true;
  17.         }
  18.         return true;
  19.     }
  20.     bool change(string first, string second) {
  21.         int n=0;
  22.         for(int i=0;i<second.length();i++){
  23.             if(first[i]!=second[i])n++;
  24.             if(n>1)return false;
  25.         }
  26.         return true;
  27.     }
  28. };

面试题 01.06. 字符串压缩

字符串压缩。利用字符重复出现的次数，编写一种方法，实现基本的字符串压缩功能。比如，字符串aabcccccaaa会变为a2b1c5a3。若“压缩”后的字符串没有变短，则返回原先的字符串。你可以假设字符串中只包含大小写英文字母（a至z）。

示例1:

 输入："aabcccccaaa"
 输出："a2b1c5a3"

示例2:

 输入："abbccd"
 输出："abbccd"
 解释："abbccd"压缩后为"a1b2c2d1"，比原字符串长度更长。

提示：

  1. 字符串长度在[0, 50000]范围内。
  1. class Solution {
  2. public:
  3.     string compressString(string s) {
  4.         auto s2=compress(s);
  5.         return s2.length()<s.length()?s2:s;
  6.     }
  7.     string compress(string s) {
  8.         string ans;
  9.         char c=0;
  10.         int n=0;
  11.         for(auto si:s){
  12.             if(si==c)n++;
  13.             else{
  14.                 if(n)ans+=c+to_string(n);
  15.                 c=si,n=1;
  16.             }
  17.         }
  18.         return ans+c+to_string(n);
  19.     }
  20. };

面试题 01.07. 旋转矩阵

48. 旋转图像

面试题 01.08. 零矩阵

编写一种算法，若M × N矩阵中某个元素为0，则将其所在的行与列清零。

示例 1：

输入：
[
  [1,1,1],
  [1,0,1],
  [1,1,1]
]
输出：
[
  [1,0,1],
  [0,0,0],
  [1,0,1]
]

示例 2：

输入：
[
  [0,1,2,0],
  [3,4,5,2],
  [1,3,1,5]
]
输出：
[
  [0,0,0,0],
  [0,4,5,0],
  [0,3,1,0]
]
  1. class Solution {
  2. public:
  3.     void setZeroes(vector<vector<int>>& matrix) {
  4.         vector<int>r(matrix.size());
  5.         vector<int>c(matrix[0].size());
  6.         for(int i=0;i<matrix.size();i++){
  7.             for(int j=0;j<matrix[0].size();j++){
  8.                 if(matrix[i][j]==0)r[i]=1,c[j]=1;
  9.             }
  10.         }
  11.         for(int i=0;i<matrix.size();i++){
  12.             for(int j=0;j<matrix[0].size();j++){
  13.                 if(r[i]||c[j])matrix[i][j]=0;
  14.             }
  15.         }
  16.     }
  17. };

面试题 01.09. 字符串轮转

KMP

面试题 02.01. 移除重复节点

单链表

面试题 02.02. 返回倒数第 k 个节点

rust

面试题 02.03. 删除中间节点

若链表中的某个节点，既不是链表头节点，也不是链表尾节点，则称其为该链表的「中间节点」。

假定已知链表的某一个中间节点，请实现一种算法，将该节点从链表中删除。

例如，传入节点 c（位于单向链表 a->b->c->d->e->f 中），将其删除后，剩余链表为 a->b->d->e->f

示例：

输入：节点 5 （位于单向链表 4->5->1->9 中）
输出：不返回任何数据，从链表中删除传入的节点 5，使链表变为 4->1->9

  1. class Solution {
  2. public:
  3.     void deleteNode(ListNode* node) {
  4.         node->val=node->next->val;
  5.         node->next=node->next->next;
  6.     }
  7. };

面试题 02.04. 分割链表

单链表

面试题 02.05. 链表求和

单链表

面试题 02.06. 回文链表

单链表

面试题 02.07. 链表相交

单链表

面试题 02.08. 环路检测

142. 环形链表 II

面试题 03.02. 栈的最小值

单调栈

面试题 04.01. 节点间通路

rust

面试题 04.02. 最小高度树

rust

面试题 04.03. 特定深度节点链表

二叉树BFS

面试题 04.04. 检查平衡性

力扣 110. 平衡二叉树

面试题 04.05. 合法二叉搜索树

二叉搜索树 二叉搜索树（BST）_csuzhucong的博客-CSDN博客

面试题 04.06. 后继者

二叉树DFS

面试题 04.08. 首个共同祖先

lca

面试题 05.03. 翻转数位

给定一个32位整数 num，你可以将一个数位从0变为1。请编写一个程序，找出你能够获得的最长的一串1的长度。

示例 1：

输入: num = 1775(110111011112)
输出: 8

示例 2：

输入: num = 7(01112)
输出: 4
  1. class Solution {
  2. public:
  3.     int reverseBits(unsigned num) {
  4.         vector<int>v;
  5.         int n=0,ans=0;
  6.         while(num){
  7.             if(num&1)n++;
  8.             else{
  9.                 if(n)v.push_back(n),n=0;
  10.                 else ans=max(ans,maxLen(v)),v.clear();
  11.             }
  12.             num/=2;
  13.         }
  14.         v.push_back(n);
  15.         return min(32,max(ans,maxLen(v)));
  16.     }
  17.     int maxLen(vector<int>&v){
  18.         if(v.empty())return 1;
  19.         if(v.size()==1)return v[0]+1;
  20.         int ans=0;
  21.         for(int i=1;i<v.size();i++)ans=max(ans,v[i]+v[i-1]+1);
  22.         return ans;
  23.     }
  24. };

面试题 05.04. 下一个数

下一个数。给定一个正整数，找出与其二进制表达式中1的个数相同且大小最接近的那两个数（一个略大，一个略小）。

示例1:

 输入：num = 2（或者0b10）
 输出：[4, 1] 或者（[0b100, 0b1]）
示例2:

 输入：num = 1
 输出：[2, -1]
提示:

num的范围在[1, 2147483647]之间；
如果找不到前一个或者后一个满足条件的正数，那么输出 -1。

思路：

nextGreaterElement函数是从 力扣OJ 556. 下一个更大元素 III 略改而成。

只需要改2个地方，一个是十进制改成二进制，一个是二进制字符串前面添0。

nextLesserElement函数是nextGreaterElement函数直接修改得到，代码逻辑是一样的。
 

  1.     int nextGreaterElement(int n) {
  2.         char sn[40];
  3.         for(int i=0;i<32;i++)sn[i]=((n&(1<<31-i))?'1':'0');
  4.         sn[32]='\0';
  5.         if(!next_permutation(sn,sn+32))return -1;
  6.         long long res = StrToInt(sn,2);
  7.         if(res==int(res))return res;
  8.         return -1;
  9.     }
  10.     int nextLesserElement(int n) {
  11.         char sn[40];
  12.         for(int i=0;i<32;i++)sn[i]=((n&(1<<31-i))?'1':'0');
  13.         sn[32]='\0';
  14.         if(!prev_permutation(sn,sn+32))return -1;
  15.         long long res = StrToInt(sn,2);
  16.         if(res==int(res))return res;
  17.         return -1;
  18.     }
  19.  
  20. class Solution {
  21. public:
  22.     vector<int> findClosedNumbers(int num) {
  23.         vector<int> ans(2);
  24.         ans[1]=nextLesserElement(num);
  25.         ans[0]=nextGreaterElement(num);
  26.         return ans;
  27.     }
  28. };

面试题 05.06. 整数转换

二进制

面试题 05.08. 绘制直线

题目：

绘制直线。有个单色屏幕存储在一个一维数组中，使得32个连续像素可以存放在一个 int 里。屏幕宽度为w，且w可被32整除（即一个 int 不会分布在两行上），屏幕高度可由数组长度及屏幕宽度推算得出。请实现一个函数，绘制从点(x1, y)到点(x2, y)的水平线。

给出数组的长度 length，宽度 w（以比特为单位）、直线开始位置 x1（比特为单位）、直线结束位置 x2（比特为单位）、直线所在行数 y。返回绘制过后的数组。

示例1:

 输入：length = 1, w = 32, x1 = 30, x2 = 31, y = 0
 输出：[3]
 说明：在第0行的第30位到第31为画一条直线，屏幕表示为[0b000000000000000000000000000000011]
示例2:

 输入：length = 3, w = 96, x1 = 0, x2 = 95, y = 0
 输出：[-1, -1, -1]

代码：
 

  1. class Solution {
  2. public:
  3.     vector<int> drawLine(int length, int w, int x1, int x2, int y) {
  4.         vector<int>ans;
  5.         int s=x1/32+w/32*y,e=x2/32+w/32*y;
  6.         for(int i=0;i<s;i++)ans.insert(ans.end(),0);
  7.         for(int i=s;i<=e;i++)ans.insert(ans.end(),-1);
  8.         for(int i=e+1;i<length;i++)ans.insert(ans.end(),0);
  9.         x1=32-x1%32,x2=31-x2%32;
  10.         long long a=1;
  11.         ans[s]&=int((a<<x1)-1),ans[e]&=(-(1<<x2));
  12.         return ans;
  13.     }
  14. };

面试题 08.01. 三步问题

三步问题。有个小孩正在上楼梯，楼梯有n阶台阶，小孩一次可以上1阶、2阶或3阶。实现一种方法，计算小孩有多少种上楼梯的方式。结果可能很大，你需要对结果模1000000007。

示例1:

 输入：n = 3 
 输出：4
 说明: 有四种走法

示例2:

 输入：n = 5
 输出：13

提示:

  1. n范围在[1, 1000000]之间
  1. class Solution {
  2. public:
  3.     int waysToStep(int n) {
  4.         vector<int>v(n+10);
  5.         v[0]=1,v[1]=1,v[2]=2,v[3]=4;
  6.         for(int i=4;i<=n;i++)v[i]=((v[i-1]+v[i-2])%1000000007+v[i-3])%1000000007;
  7.         return v[n];
  8.     }
  9. };

面试题 08.04. 幂集

幂集。编写一种方法，返回某集合的所有子集。集合中不包含重复的元素。

说明：解集不能包含重复的子集。

示例:

 输入： nums = [1,2,3]
 输出：
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]
  1. class Solution {
  2. public:
  3.     vector<vector<int>> subsets(vector<int>& nums) {
  4.         return GetAllSubsets(nums,false);
  5.     }
  6. };

面试题 08.05. 递归乘法

二进制

面试题 08.06. 汉诺塔问题

rust

面试题 08.11. 硬币

硬币。给定数量不限的硬币，币值为25分、10分、5分和1分，编写代码计算n分有几种表示法。(结果可能会很大，你需要将结果模上1000000007)

示例1:

 输入: n = 5
 输出：2
 解释: 有两种方式可以凑成总金额:
5=5
5=1+1+1+1+1

示例2:

 输入: n = 10
 输出：4
 解释: 有四种方式可以凑成总金额:
10=10
10=5+5
10=5+1+1+1+1+1
10=1+1+1+1+1+1+1+1+1+1

说明：

注意:

你可以假设：

  • 0 <= n (总金额) <= 1000000
  1. class Solution {
  2. public:
  3. 	int waysToChange(int n) {
  4. 		vector<int>coins{ 25,10,5,1 };
  5. 		return DP_CoinCombine(coins, n, 1000000007);
  6. 	}
  7. };

面试题 08.12. 八皇后

51. N皇后

面试题 08.14. 布尔运算

区间DP

面试题 10.01. 合并排序的数组

给定两个排序后的数组 A 和 B，其中 A 的末端有足够的缓冲空间容纳 B。 编写一个方法，将 B 合并入 A 并排序。

初始化 A 和 B 的元素数量分别为 m 和 n。

示例:

输入:
A = [1,2,3,0,0,0], m = 3
B = [2,5,6],       n = 3

输出: [1,2,2,3,5,6]

说明:

  • A.length == n + m
  1. class Solution {
  2. public:
  3.     void merge(vector<int>& A, int m, vector<int>& B, int n) {
  4.         for(int i=0;i<n;i++)A[i+m]=B[i];
  5.         sort(A.begin(),A.end());
  6.     }
  7. };

面试题 10.03. 搜索旋转数组

搜索旋转数组。给定一个排序后的数组，包含n个整数，但这个数组已被旋转过很多次了，次数不详。请编写代码找出数组中的某个元素，假设数组元素原先是按升序排列的。若有多个相同元素，返回索引值最小的一个。

示例1:

 输入: arr = [15, 16, 19, 20, 25, 1, 3, 4, 5, 7, 10, 14], target = 5
 输出: 8（元素5在该数组中的索引）
示例2:

 输入：arr = [15, 16, 19, 20, 25, 1, 3, 4, 5, 7, 10, 14], target = 11
 输出：-1 （没有找到）
提示:

arr 长度范围在[1, 1000000]之间

  1. class Solution {
  2. public:
  3. 	int search(vector<int>& nums, int target) {
  4. 		for(int i=0;i<nums.size();i++)if(nums[i]==target)return i;
  5. 		return -1;
  6. 	}
  7. };

面试题 16.03. 交点

计算几何

面试题 16.04. 井字游戏

圈叉棋

面试题 16.05. 阶乘尾数

设计一个算法，算出 n 阶乘有多少个尾随零。

示例 1:

输入: 3
输出: 0
解释: 3! = 6, 尾数中没有零。
示例 2:

输入: 5
输出: 1
解释: 5! = 120, 尾数中有 1 个零.
说明: 你算法的时间复杂度应为 O(log n) 。

  1. class Solution {
  2. public:
  3. 	int trailingZeroes(int n) {
  4. 		if (n < 5)return 0;
  5. 		return n / 5 + trailingZeroes(n / 5);
  6. 	}
  7. };

面试题 16.06. 最小差

双指针

面试题 16.07. 最大数值

编写一个方法，找出两个数字a和b中最大的那一个。不得使用if-else或其他比较运算符。

示例：

输入： a = 1, b = 2
输出： 2
  1. class Solution {
  2. public:
  3.     int maximum(int a, int b) {
  4.         long long c=a;
  5.         int flag=(unsigned long long)(c-b)>>63;
  6.         return a+(b-c)*flag;
  7.     }
  8. };

面试题 16.08. 整数的英语表示

273. 整数转换英文表示

面试题 16.13. 平分正方形

计算几何

面试题 16.16. 部分排序

给定一个整数数组，编写一个函数，找出索引m和n，只要将索引区间[m,n]的元素排好序，整个数组就是有序的。注意：n-m尽量最小，也就是说，找出符合条件的最短序列。函数返回值为[m,n]，若不存在这样的m和n（例如整个数组是有序的），请返回[-1,-1]。

示例：

输入： [1,2,4,7,10,11,7,12,6,7,16,18,19]
输出： [3,9]

提示：

  • 0 <= len(array) <= 1000000
  1. class Solution {
  2. public:
  3.     vector<int> subSort(vector<int>& array) {
  4.         vector<int>v=array;
  5.         sort(v.begin(),v.end());
  6.         int low=0,high=v.size()-1;
  7.         while(low <v.size() && v[low]==array[low])low++;
  8.         if(low==v.size())return vector<int>{-1,-1};
  9.         while(low <high && v[high]==array[high])high--;
  10.         return vector<int>{low,high};
  11.     }
  12. };

面试题 16.17. 连续数列

给定一个整数数组，找出总和最大的连续数列，并返回总和。

示例：

输入： [-2,1,-3,4,-1,2,1,-5,4]
输出： 6
解释： 连续子数组 [4,-1,2,1] 的和最大，为 6。

进阶：

如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

  1. class Solution {
  2. public:
  3.     int maxSubArray(vector<int>& nums) {
  4.         return DP_MaxSubArray::maxSubArray(nums);
  5.     }
  6. };

面试题 16.19. 水域大小

并查集

面试题 16.20. T9键盘

在老式手机上，用户通过数字键盘输入，手机将提供与这些数字相匹配的单词列表。每个数字映射到0至4个字母。给定一个数字序列，实现一个算法来返回匹配单词的列表。你会得到一张含有有效单词的列表。映射如下图所示：

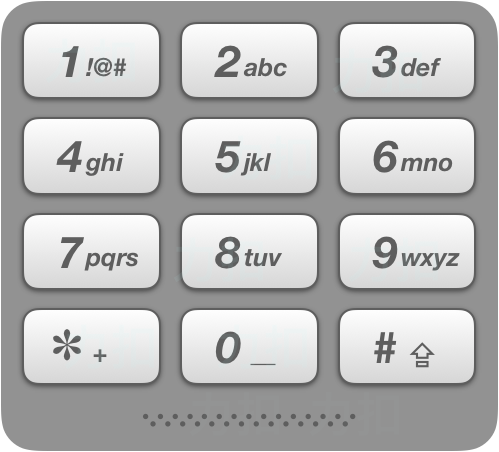
示例 1:

输入: num = "8733", words = ["tree", "used"]
输出: ["tree", "used"]

示例 2:

输入: num = "2", words = ["a", "b", "c", "d"]
输出: ["a", "b", "c"]

提示：

  • num.length <= 1000
  • words.length <= 500
  • words[i].length == num.length
  • num中不会出现 0, 1 这两个数字
  1. class Solution {
  2. public:
  3. 	vector<string> getValidT9Words(string num, vector<string>& words) {
  4. 		vector<string>ans;
  5. 		for(auto s:words){
  6. 			if (trans(s) == num)ans.push_back(s);
  7. 		}
  8. 		return ans;
  9. 	}
  10. 	string trans(string s) {
  11. 		string ans = "";
  12. 		for (auto c : s)ans += trans(c);
  13. 		return ans;
  14. 	}
  15. 	char trans(char c) {
  16. 		if (c == 's')return '7';
  17. 		if (c == 'v')return '8';
  18. 		if (c > 'v')return '9';
  19. 		char x = '2';
  20. 		return x + (c - 'a') / 3;
  21. 	}
  22. };

面试题 16.21. 交换和

给定两个整数数组，请交换一对数值（每个数组中取一个数值），使得两个数组所有元素的和相等。

返回一个数组，第一个元素是第一个数组中要交换的元素，第二个元素是第二个数组中要交换的元素。若有多个答案，返回任意一个均可。若无满足条件的数值，返回空数组。

示例:

输入: array1 = [4, 1, 2, 1, 1, 2], array2 = [3, 6, 3, 3]
输出: [1, 3]

示例:

输入: array1 = [1, 2, 3], array2 = [4, 5, 6]
输出: []

提示：

  • 1 <= array1.length, array2.length <= 100000
  1. class Solution {
  2. public:
  3. 	vector<int> findSwapValues(vector<int>& array1, vector<int>& array2) {
  4. 		int d = 0;
  5. 		set<int>s;
  6. 		for (auto x : array1)d += x, s.insert(x);
  7. 		for (auto x : array2)d -= x;
  8. 		if (d & 1)return vector<int>{};
  9. 		d /= 2;
  10. 		for (auto x : array2) {
  11. 			if (s.find(x + d) != s.end())return vector<int>{x + d, x};
  12. 		}
  13. 		return vector<int>{};
  14. 	}
  15. };

面试题 16.22. 兰顿蚂蚁

兰顿蚂蚁

面试题 16.25. LRU 缓存

146. LRU 缓存机制

面试题 17.01. 不用加号的加法

设计一个函数把两个数字相加。不得使用 + 或者其他算术运算符。

示例:

输入: a = 1, b = 1
输出: 2

提示：

  • a, b 均可能是负数或 0
  • 结果不会溢出 32 位整数
  1. class Solution {
  2. public:
  3.     int add(unsigned a, unsigned b) {
  4.         int x=1,s=0,flag=0;
  5.         while(true){
  6.             int a2=a&x;
  7.             int b2=b&x;
  8.             if(!a2&&!b2){
  9.                 if(flag)s^=x;
  10.                 flag=0;
  11.             }else if(a2&&b2){
  12.                 if(flag)s^=x;
  13.                 flag=1;
  14.             }else{
  15.                 if(!flag)s^=x,flag=0;
  16.             }
  17.             if(x==(1<<31))break;
  18.             x=x<<1;
  19.         }
  20.         return s;
  21.     }
  22. };

面试题 17.04. 消失的数字

268. 缺失数字

面试题 17.05. 字母与数字

给定一个放有字母和数字的数组，找到最长的子数组，且包含的字母和数字的个数相同。

返回该子数组，若存在多个最长子数组，返回左端点下标值最小的子数组。若不存在这样的数组，返回一个空数组。

示例 1:

输入: ["A","1","B","C","D","2","3","4","E","5","F","G","6","7","H","I","J","K","L","M"]

输出: ["A","1","B","C","D","2","3","4","E","5","F","G","6","7"]

示例 2:

输入: ["A","A"]

输出: []

提示：

  • array.length <= 100000
  1. class Solution {
  2. public:
  3.     vector<string> findLongestSubarray(vector<string>& array) {
  4.         map<int,int>m;
  5.         m[0]=-1;
  6.         int dif=0,low=0,high=0;
  7.         for(int i=0;i<array.size();i++){
  8.             if(array[i][0]>='0'&&array[i][0]<='9')dif++;
  9.             else dif--;
  10.             if(m.find(dif)==m.end())m[dif]=i;
  11.             if(i-m[dif]>high-low)low=m[dif],high=i;
  12.         }
  13.         vector<string>ans;
  14.         if(high)for(int i=low+1;i<=high;i++)ans.push_back(array[i]);
  15.         return ans;
  16.     }
  17. };

面试题 17.06. 2出现的次数

数位DP

面试题 17.07. 婴儿名字

并查集

面试题 17.09. 第 k 个数

数论问题

面试题 17.12. BiNode

二叉搜索树

面试题 17.14. 最小K个数

设计一个算法，找出数组中最小的k个数。以任意顺序返回这k个数均可。

示例：

输入： arr = [1,3,5,7,2,4,6,8], k = 4
输出： [1,2,3,4]

提示：

  • 0 <= len(arr) <= 100000
  • 0 <= k <= min(100000, len(arr))
  1. class Solution {
  2. public:
  3.     vector<int> smallestK(vector<int>& arr, int k) {
  4.         sort(arr.begin(),arr.end());
  5.         arr.resize(k);
  6.         return arr;
  7.     }
  8. };

面试题 17.17. 多次搜索

KMP

面试题 17.19. 消失的两个数字

搜索else

面试题 17.20. 连续中值

力扣 295. 数据流的中位数

面试题 17.21. 直方图的水量

力扣 42. 接雨水

面试题 17.26. 稀疏相似度

两个(具有不同单词的)文档的交集(intersection)中元素的个数除以并集(union)中元素的个数，就是这两个文档的相似度。例如，{1, 5, 3} 和 {1, 7, 2, 3} 的相似度是 0.4，其中，交集的元素有 2 个，并集的元素有 5 个。给定一系列的长篇文档，每个文档元素各不相同，并与一个 ID 相关联。它们的相似度非常“稀疏”，也就是说任选 2 个文档，相似度都很接近 0。请设计一个算法返回每对文档的 ID 及其相似度。只需输出相似度大于 0 的组合。请忽略空文档。为简单起见，可以假定每个文档由一个含有不同整数的数组表示。

输入为一个二维数组 docs，docs[i] 表示 id 为 i 的文档。返回一个数组，其中每个元素是一个字符串，代表每对相似度大于 0 的文档，其格式为 {id1},{id2}: {similarity}，其中 id1 为两个文档中较小的 id，similarity 为相似度，精确到小数点后 4 位。以任意顺序返回数组均可。

示例:

输入: 

  1. [
  2.   [14, 15, 100, 9, 3],
  3.   [32, 1, 9, 3, 5],
  4.   [15, 29, 2, 6, 8, 7],
  5.   [7, 10]
  6. ]

输出:
[
  "0,1: 0.2500",
  "0,2: 0.1000",
  "2,3: 0.1429"
]

提示：

  • docs.length <= 500
  • docs[i].length <= 500
  1. class Solution {
  2. public:
  3. 	vector<string> computeSimilarities(vector<vector<int>>& docs) {
  4. 		for (auto &vi : docs) {
  5. 			sort(vi.begin(), vi.end());
  6. 		}
  7. 		vector<string>ans;
  8. 		for (int i = 0; i < docs.size(); i++) {
  9. 			for (int j = i + 1; j < docs.size(); j++) {
  10. 				double x = simi(docs[i], docs[j]);
  11. 				std::stringstream stream{};
  12. 				stream << std::fixed << std::setprecision(4) << int(x * 10000 + 0.5) / 10000.0;
  13. 				if (x)ans.push_back(to_string(i) + "," + to_string(j) + ": " + stream.str());
  14. 			}
  15. 		}
  16. 		return ans;
  17. 	}
  18. 	double simi(vector<int>&v1, vector<int>&v2) {
  19. 		if (v1.empty() || v2.empty())return 0;
  20. 		int n = 0;
  21. 		for (int i = 0, j = 0; i < v1.size() && j < v2.size();) {
  22. 			if (v1[i] < v2[j])i++;
  23. 			else if (v1[i] > v2[j])j++;
  24. 			else n++, i++, j++;
  25. 		}
  26. 		return n * 1.0 / (v1.size() + v2.size() - n);
  27. 	}
  28. };

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/不正经/article/detail/488923
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号