不正经

这个屌丝很懒，什么也没留下！

热门标签

算法练习day4

作者：不正经 | 2024-05-12 18:19:08

踩

算法练习day4

前言

中间个人原因断了很久，现在回来继续。。。。

两两交换链表中的节点

代码随想录两两交换链表中的节点

24. 两两交换链表中的节点 - 力扣（LeetCode）

（用时：0.3小时）

思路

这道题的思路其实很简单，两两节点交换，注意在交换前提前保存好可能会断链的节点即可。

同时也需要注意节点交换的顺序问题，其他的就没什么。

至于递归实现，后续有时间再说吧。。。

代码实现


/// <summary>
/// 三指针交换
/// </summary>
/// <param name="head"></param>
/// <returns></returns>
public ListNode SwapPairs(ListNode head)
{
    ListNode visHeadNode, tempNode, curNode;
    visHeadNode = new ListNode();
    visHeadNode.next = head;
    curNode = visHeadNode;
    while(curNode.next!=null && curNode.next.next!=null)
    {
        tempNode = curNode.next.next;
        curNode.next.next = tempNode.next;
        tempNode.next = curNode.next;
        curNode.next = tempNode;
        curNode = tempNode.next;                
    }
    return visHeadNode.next;
}

删除链表的倒数第N个节点

代码随想录删除链表的倒数第N个节点

19. 删除链表的倒数第 N 个结点 - 力扣（LeetCode）

（用时：0.5小时）

思路

这道题用快慢指针法，即只遍历一次就找到倒数第n个节点。（假设链表长度为N，那么就是找到正数第N-n个节点）

快指针与慢指针始终相差N-n+1个节点。
快指针向前探索，直到到达链表结尾（结尾节点的next为null）
慢指针先和快指针拉开N-n+1个节点的距离，随后跟随着快指针的脚步向后遍历即可。
两个指针相差N-n+1，是因为在去除倒数第n个节点（正数第N-n个节点）时，需要通过其前驱节点，因此需要少前进一步。
即需要找到并让fastNode指向第N-n+1个节点，也可以说fastNode需要先走n+1步

易错/错误点

本题思路其实不难，但在临界值方面和容易出错，因此需要格外注意。自己也是在这里踩坑了。。。

易错或者说比较重要的点有几个：

赋初始值时，fastNode和slowNode的初始值究竟是什么好呢？
第一个while的判断条件中，n的条件是n>=0还是n>0呢？
第二个while的判断条件

个人的理解如下：

n的判断条件

fastNode需要在第一个while中与slowNode拉开n个节点的距离。对于n的判断条件，n每循环一次就-1。当n=0时，fastNode走了n步，fastNode需要先走n+1步，因此while需要再循环一次，n=0成立。
fastNode的初始值

fastNode要么是visHeadNode，要么是visHeadNode.next。visHeadNode.next就是链表真实头节点。

此时我们需要明白一个问题，先做个假设，假设链表有3个节点，让slow和fast分别在链表的头和尾处：

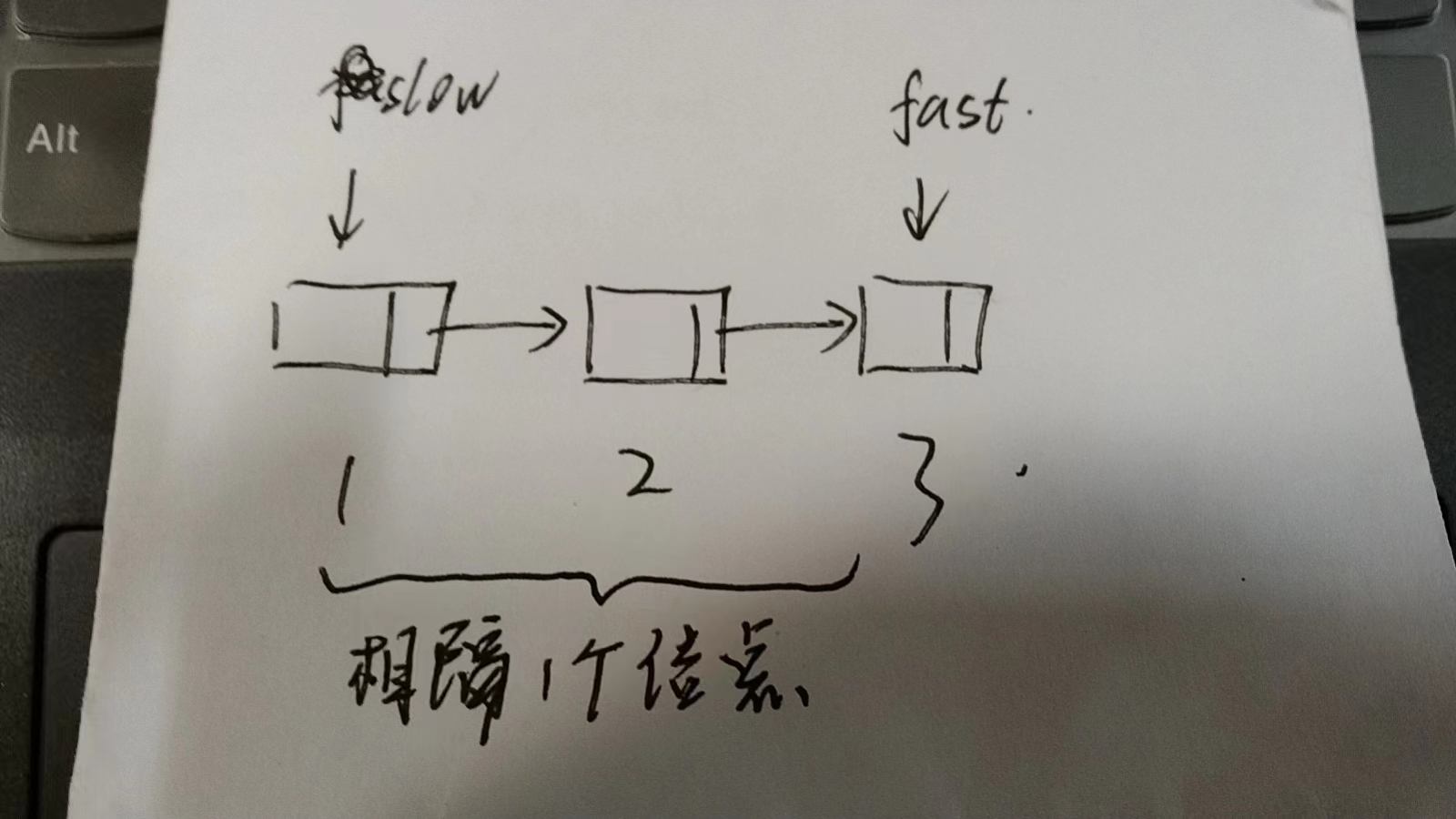
可以发现，链表长度为3，而slow和fast之间相隔1个节点。这说明链表的头和尾之间是相隔n-2个节点。

回到fastNode的初始值问题，假设题目的链表就是如上图所示，如果需要删除的是倒数第3个节点（即真实头节点）：当fastNode=visHeadNode.next（即fastNode=真实头节点）。当n自减到1时，fastNode已经指向了末尾。此时固然可以让第一个while里多一个fast.next!=null的判断条件，第一二个while均可正确通过。但是需要注意最后的移除节点步骤，slowNode是需要移除节点的前驱节点，按照这个逻辑，我们将把第一个节点删除，它是链表的倒数第2个，这与我们的目标不符，这里就出了问题。因此，我们需要让fastNode的初始值为visHeadNode。
slowNode的初始值

slowNode在第二个while循环中才需要让其开始遍历，在此之前是没有更改的。slowNode的初始值需要和fastNode一样，因为都是从“头”开始遍历嘛。
第二个while中的判断条件

第二个while的逻辑是让slow和fast向前遍历，直到fastNode找到链表尾节点。链表尾节点的条件是fastNode.next!=null，因此这就是判断条件。

代码实现

快慢指针法：


/// <summary>
/// 快慢指针法
/// </summary>
/// <param name="head"></param>
/// <param name="n"></param>
/// <returns></returns>
public ListNode RemoveNthFromEnd(ListNode head, int n)
{
    ListNode visHeadNode, fastNode, slowNode;
    visHeadNode = new ListNode();
    visHeadNode.next = head;
    fastNode = visHeadNode;
    slowNode = visHeadNode;
    while (n > 0)
    {
        fastNode = fastNode.next;
        n--;
    }
    while(fastNode.next!=null)
    {
        slowNode = slowNode.next;
        fastNode = fastNode.next;
    }
    slowNode.next = slowNode.next.next;
    return visHeadNode.next;
}

链表相交

代码随想录面试题 20.07链表相交

面试题 02.07. 链表相交 - 力扣（LeetCode）

（用时：3小时）

思路

本道题刚开始只想到双重循环的暴力搜索方法，后来看了卡哥的视频后，原来还可以通过链表长度来实现。

此外，在网站上看C#题解样例时，看到了另外一个很有意思的解法。自己画图后发现，这位大佬用的是环形链表的方法。

链表长度同步移动法

两链表若有相交，那么从相交的节点开始往后应均为一样。

假设较短的链表从头节点开始便以相交，那么较短链表长度即为相交链表可能的最大长度，这样能一定程度上降低时间复杂度。

总结来说，首先需要得到较短链表的长度，接着让较长链表的指针从与较短链表长度一样的节点开始，最后让两个链表的指针同时向后探索扫描，当指向同一个节点时便找到了相交链表的头节点。

错误

看是看懂了，但是在写的时候还是犯了一些错误：

指针遍历写错了（这个错误只能说是大晚上脑子不清醒吧。。。自己都无语了。。）
求得短的链表长度后，只动长链表的指针即可。

反思后的理解如下：

求得短的链表长度后，只动长链表的指针即可。

这里刚开始让两个指针都在动，导致了短链表的指针到了末尾甚至空值引用了。。。两个链表的可能的相交节点位置是不固定的。求得短的链表长度后，让长的链表的指针指向开头即可，短链表的指针无需动。

合并链表追逐法

这个追逐法其实就是将两个链表首尾连在一起，如果有环，说明他们有相交。

此时这个问题就从是否相交转化成了，这一大条链表，首尾相接后，是否还有更小的环。

接着用环形链表的特性：两个指针在环形链表中始终向前跑，若环形链表有环，那么两个指针一定会相遇。（后面一题的环形链表中，卡哥有讲原理）

本道题中，两个指针没有快慢之分，那么他们一定会在两个链表开始相交的节点上相遇。

重点

此时有个很重要的问题，如果链表没有相交，那怎么判断他们没有相交？（即怎么让循环停下来）

两个链表根据他们的长度分为长度相等和长度不等的情况

长度相等：当他们共同到尾节点，他们或者他们的next均会等于null，此时就是终止条件。
长度不相等：两个指针走过的节点一个长一个短，那么让走的长一点的指针走一遍短的路、让走的短一点的指针走一遍长的路，

他们会同时走到对方链表的尾节点，他们或者他们的next均会等于null，此时就是终止条件。

代码实现

链表长度同步移动法：


/// <summary>
/// 链表长度同步移动法
/// </summary>
/// <param name="headA"></param>
/// <param name="headB"></param>
/// <returns></returns>
public ListNode GetIntersectionNode(ListNode headA, ListNode headB)
{
    ListNode curA = headA,curB = headB;
    int lenA = 0, lenB = 0;
    //得到较短链表的长度
    while (curA!=null)
    {
        lenA++;
        curA = curA.next;
    }
    
    while(curB!=null)
    {
        lenB++;
        curB = curB.next;
    }
    //设置较长链表的指针初始值
    curA = lenA > lenB ? headA : headB;
    curB = lenA > lenB ? headB : headA;
    for (int i=0;i<Math.Abs(lenA-lenB);i++)
    {
        curA = curA.next;
    }
    //两个链表的指针同时向后探索扫描
    while (curA!=null)
    {
        if (curA==curB)
        {
            return curA;
        }
        curA = curA.next;
        curB = curB.next;
    }
    return null;
}

合并链表追逐法：


/// <summary>
/// 合并链表追逐法
/// </summary>
/// <param name="headA"></param>
/// <param name="headB"></param>
/// <returns></returns>
public ListNode GetIntersectionNode2(ListNode headA, ListNode headB)
{
    ListNode curA = headA, curB = headB;
    while(curA!=curB)
    {
        curA = curA == null ? headB : curA.next;
        curB = curB == null ? headA : curB.next;
    }
    return curA;
}

环形链表

代码随想录环形链表II

142. 环形链表 II - 力扣（LeetCode）

（用时：2小时）

思路

前面链表相交也有涉及到环形链表的知识。前面理解了这里其实不是很难。

要证明链表是否有环，和前面一样提到的一样：两个指针在环形链表中始终向前跑，若环形链表有环，那么两个指针一定会相遇。

这里卡哥推导证明环形链表快慢指针如何相遇、两指针如何找入口才是重点难点。（时间问题推导就略过了，二刷时再自己推导）

错误

写的过程中犯了一些错误：

fastNode和slowNode的初始值。
while中，指针的遍历和if判断的前后位置。
为什么第二个while要嵌套在第一个while里面

个人理解如下：

fastNode和slowNode的初始值

最近写的题中，初始值的问题总是会遇到问题。fast和slow两个指针都是从head头节点开始的，在赋初始值时，一般都是按照这个思路来，无需多想让后面的逻辑方便。当后续需要再回头修改至逻辑通畅即可。
while中，指针的遍历和if判断的前后位置

（这里其实也不是说犯错了，是自己有疑惑去尝试出来后得出来的想法。）两个指针的初始值都是head，如果不先走，那么刚开始就已经是指向同一个节点了。

为什么第二个while要嵌套在第一个while里面

最开始自己的思路：在第一个while中，快慢指针向前探索，若两者相遇了，则说明有环。若没相遇，fastNode到链表末尾了，则没有环，返回null。接着fastNode指向链表头节点，在第二个while中，让两个指针以同样的速度向前遍历，相遇的节点即为环形的入口。

测试后发现，示例1和3并不能通过，能力原因暂时也没找到原因。。。当时写的代码保留了下来：


public ListNode DetectCycle(ListNode head)
{
    ListNode fastNode = head, slowNode = head;
    while (fastNode != slowNode)
    {
        fastNode = fastNode.next.next;
        slowNode = slowNode.next;
        if (fastNode == null || fastNode.next == null)
        {
            return null;
        }
    }
    fastNode = head;
    while (fastNode != slowNode)
    {
        fastNode = fastNode.next;
        slowNode = slowNode.next;
    }
    return fastNode;
}

现在时间不多，后续二刷应该会有新的理解。

代码实现


 public ListNode DetectCycle(ListNode head)
 {
     ListNode fastNode = head, slowNode = head;
     while (fastNode!=null && fastNode.next!=null)
     {
         fastNode = fastNode.next.next;
         slowNode = slowNode.next;
         if (fastNode==slowNode)
         {
             fastNode = head;
             while(fastNode!=slowNode)
             {
                 fastNode = fastNode.next;
                 slowNode = slowNode.next;
             }
             return fastNode;
         }
     }
     return null;
 }

后记

这四道题昨天（5.7）就开始写了，但能力有限吧一天下来只写完了3道题，记录也只整理回顾了前2道题的。

现在开始难度有点上来了，愈发发现自己的算法能力拉下太多了。

此后会将算法的练习作为每天最优先的任务。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/不正经/article/detail/560140