数据结构：栈「详解」_栈是一种什么数据结构

目录

 

一，栈的定义

二，栈的基本操作

1，顺序栈

1.1顺序栈的基本概念

1.2顺序栈的基本操作

2，链栈

2.1链栈的基本概念

2.2链栈的种类

2.3链栈的基本操作

三，栈的应用

1，函数递归调用

2，表达式求值

3，数制转换

4，迷宫求解

参考资料

---

 

一，栈的定义

栈（Stack）是一种常见的数据结构，它是一种“后进先出”（Last In First Out，LIFO）的数据结构。栈可以看做是一种特殊的线性表，只能在栈顶进行插入和删除操作。栈顶是允许操作的，而栈底是固定的。

二，栈的基本操作

栈的基本操作包括：入栈（Push）、出栈（Pop）、取栈顶元素（Top）和判空（IsEmpty）等。

1，顺序栈

        1.1顺序栈的基本概念

顺序栈是一种使用数组实现的栈，也称为数组栈。其基本思路是通过数组来存储栈中的元素，并通过栈顶指针指示栈顶元素在数组中的位置。顺序栈具有以下特点：

1. 存储结构：使用数组作为底层存储结构，数组的每个元素存储栈中的一个元素；
2. 操作受限：栈只能从栈顶插入和删除元素，不支持在栈中间插入和删除元素；
3. 先进后出：栈的元素遵循“先进后出”（Last In First Out, LIFO）的原则，即后插入的元素先被删除；
4. 顺序访问：只能从栈顶开始访问栈中的元素，不能从栈底或中间位置访问元素。

顺序栈的实现非常简单，可以使用数组和栈顶指针两个变量来实现。顺序栈的主要操作包括初始化、入栈、出栈、获取栈顶元素、判断栈是否为空以及获取栈中元素的数量等。由于顺序栈的存储结构是数组，因此在使用过程中需要考虑数组大小的限制，当栈中元素数量超过数组大小时，需要对数组进行扩容。

 

注意：除了遍历栈中的元素的操作时间复杂度为O(n)外，其余：入栈、出栈、取栈顶元素、判断栈是否为空操作的时间复杂度均为O(1)。

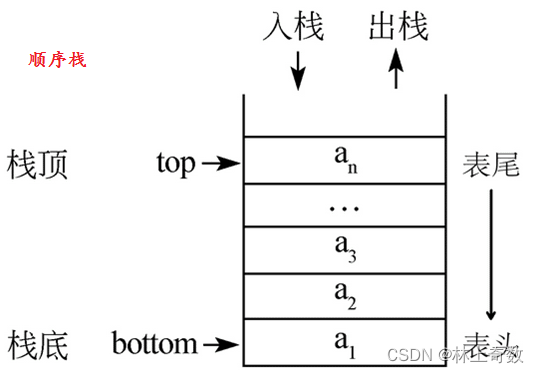
         1.2顺序栈的基本操作

相关的头文件

#include<math.h>
#include <iostream>
typedef int SElemType;
#define STACK_INIT_SIZE 10 //存储空间初始分配量
#define STACK_INCREMENT 2  //存储空间分配增量

定义顺序栈结构体

struct SqStack{ //定义顺序栈结构体
    SElemType *base; //栈底指针
    SElemType *top;  //栈顶指针
    int stacksize;   //栈可用的最大容量
};

初始化栈

void InitStack(SqStack &S){ //初始化栈S
    S.base = (SElemType*)malloc(STACK_INIT_SIZE*sizeof(SElemType)); //给栈分配空间
    if(!S.base) //如果分配失败
        exit(OVERFLOW); //则退出程序
    S.top = S.base; //栈顶指针和栈底指针指向同一个位置
    S.stacksize = STACK_INIT_SIZE; //初始化栈的最大容量
}

销毁栈

void DestoryStack(SqStack &S){ //销毁栈S
    free(S.base); //释放栈S占用的空间
    S.top = S.base = NULL; //将栈底指针和栈顶指针都置为空
    S.stacksize = 0; //将栈的最大容量清零
}

清空栈

void ClearStack(SqStack &S){ //清空栈S
    S.top = S.base; //将栈顶指针指向栈底指针，实现清空栈的效果
}

判断栈是否为空

int StackEmpty(SqStack S){ //判断栈S是否为空
    if(S.top == S.base) //如果栈顶指针和栈底指针指向同一个位置，说明栈为空
        return true;
    else
        return false;
}

返回栈长度

int StackLength(SqStack S){ //求栈S的长度
    return S.top - S.base; //栈顶指针减去栈底指针的差即为栈的长度
}

获取栈顶元素值

int GetTop(SqStack S,SElemType &e){ //获取栈顶元素，并将其存储到e中
    if (S.top > S.base){ //如果栈不为空
        e = *(S.top-1); //将栈顶元素存储到e中
        return true;
    }
    else
        return false;
}

入栈

void Push(SqStack &S,SElemType e){ //在栈顶插入元素e
    if(S.top - S.base == S.stacksize){ //如果栈满
        S.base = (SElemType*)realloc(S.base, (S.stacksize+STACK_INCREMENT)*sizeof(SElemType)); //给栈扩容
        if(!S.base) //如果扩容失败
            exit(OVERFLOW); //则退出程序
        S.top = S.base + S.stacksize; //将栈顶指针指向扩容后的栈顶
        S.stacksize += STACK_INCREMENT; //更新栈的最大容量
    }
    *(S.top)++ = e; //将元素e插入栈顶，并将栈顶指针上移一位
}

出栈

// 如果栈为空，返回false；否则返回true
int Pop(SqStack &S,SElemType &e){
    if(S.top == S.base) //栈空
        return false;
    e = *(--S.top); //将栈顶元素赋给e，栈顶指针下移一个存储单元
    return true;
}

遍历打印栈内元素

// 定义一个函数visit，用于打印元素
void visit(SElemType e)
{
    std::cout << e << " ";
}
 
// 定义一个函数用于遍历栈中的元素并对每个元素执行visit函数
void StackTraverse(SqStack S,void(*visit)(SElemType)){
    SElemType *p = S.base;
    while(S.top > p) //p指向栈元素
        visit(*p++); //对该栈调用visit()，p指针上移一个存储单元
    printf("\n");
}

主函数

int main() {
    int j;
    SqStack s;
    SElemType e;
    InitStack(s);
    for(j = 1; j <= 12; j++)
        Push(s, j);
    printf("栈中元素依次为\n");
    StackTraverse(s, visit);
    Pop(s,e);
    printf("弹出的栈顶元素e = %d\n",e);
    printf("栈空否? %d (1:空 0:否)\n",StackEmpty(s));
    GetTop(s, e);
    printf("栈顶元素e = %d,栈的长度为%d\n",e,StackLength(s));
    ClearStack(s);
    printf("清空栈后，栈空否? %d (1:空 0:否)\n",StackEmpty(s));
    DestoryStack(s);
    printf("销毁栈后，s.top = %u,s.base = %u,s.stacksize = %d\n",s.top,s.base,s.stacksize);
}

2，链栈

        2.1链栈的基本概念

链栈是一种基于链表实现的栈，其特点是无需事先分配固定长度的存储空间，栈的长度可以动态增长或缩小，避免了顺序栈可能存在的空间浪费和存储溢出问题。

 

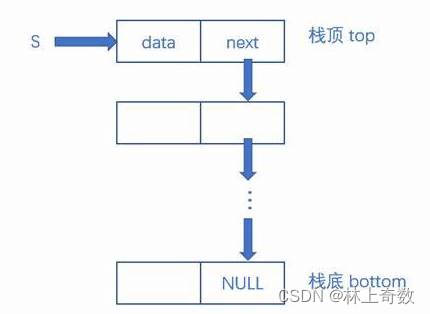
链栈中的每个元素称为“节点”，每个节点包括两个部分：数据域和指针域。数据域用来存储栈中的元素值，指针域用来指向栈顶元素所在的节点。

 

链栈的基本操作包括入栈、出栈、获取栈顶元素和遍历等，相比顺序栈而言，链栈的实现难度稍高，但其在某些情况下有着更好的灵活性和效率，特别适用于在动态存储空间较为紧缺的场合。

 

链栈的进栈push和出栈pop操作都很简单，时间复杂度均为O(1)

注意：如果栈的使用过程中元素变化不可预料,那么最好使用链栈,反之,如果它的变化在可控范围内,建议使用顺序栈。

 

        2.2链栈的种类

链栈按照链表的实现方式可分为单链栈和双链栈。实际应用通常采用单链栈。

 

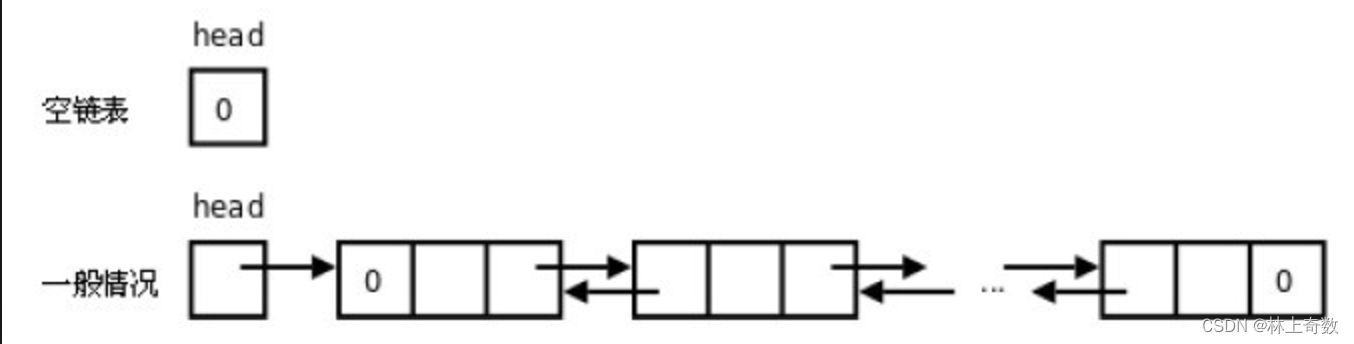
单链栈使用单链表实现，每个节点只含有一个指向下一个节点的指针。因此，单链栈只能从栈顶进行插入和删除操作。

双链栈使用双向链表实现，每个节点同时包含指向前一个节点和后一个节点的指针。因此，双链栈既可以从栈顶进行插入和删除操作，也可以从栈底进行插入和删除操作，使得操作更加灵活。

         2.3链栈的基本操作

单链栈的类型定义

// 定义链栈的结构体
typedef struct StackNode{
    SElemType data;
    StackNode *next;
}StackNode,*LinkStack;

单链栈初始化

// 初始化链栈
int InitStack(LinkStack &S){
    S = NULL;
    return true;
}

判断单链栈是否为空

// 判断链栈是否为空
bool StackEmpty(LinkStack S){
    return S == NULL;
}

单链栈入栈

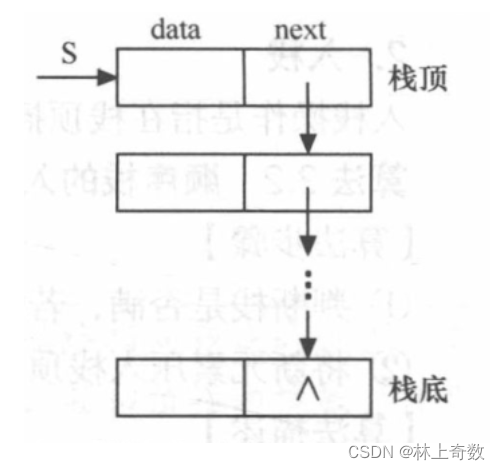
// 入栈
bool Push(LinkStack &S, SElemType e){
    StackNode *p = (StackNode*)malloc(sizeof(StackNode));
    if(!p){
        return false; // 分配内存失败
    }
    p->data = e;
    p->next = S;
    S = p;
    return true;
}

 单链栈出栈

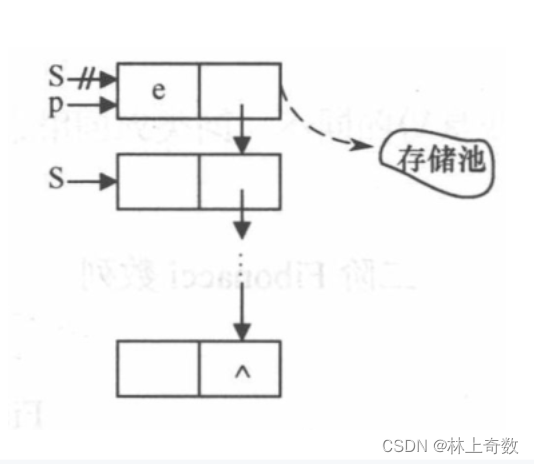
// 出栈
bool Pop(LinkStack &S, SElemType &e){
    if(StackEmpty(S)){
        return false; // 栈为空
    }
    StackNode *p = S;
    e = p->data;
    S = S->next;
    free(p);
    return true;
}

获取单链栈栈顶元素

// 获取栈顶元素
bool GetTop(LinkStack S, SElemType &e){
    if(StackEmpty(S)){
        return false; // 栈为空
    }
    e = S->data;
    return true;
}

清空单链栈

// 清空栈
void ClearStack(LinkStack &S){
    StackNode *p;
    while(S){
        p = S;
        S = S->next;
        free(p);
    }
}

销毁单链栈

// 销毁栈
void DestroyStack(LinkStack &S){
    ClearStack(S);
    S = NULL;
}

遍历单链栈

// 遍历栈并打印
void StackTraverse(LinkStack S){
    StackNode *p = S;
    while(p){
        printf("%d ", p->data);
        p = p->next;
    }
    printf("\n");
}

测试代码

#include <iostream>
 
int main() {
    LinkStack S;
    InitStack(S);
    int e;
    Push(S, 1);
    Push(S, 2);
    Push(S, 3);
    printf("现在栈内元素为(后进先出)：");
    StackTraverse(S);
    printf("栈顶元素为：%d\n", GetTop(S,e));
    Pop(S,e);
    printf("现在栈内元素为(后进先出)：");
    StackTraverse(S);
    printf("弹出一个元素后，栈顶元素为：%d\n", GetTop(S,e));
    ClearStack(S);
    if (StackEmpty(S)) {
        printf("栈为空\n");
    } else {
        printf("栈不为空\n");
    }
    DestroyStack(S);
    return 0;
}

三，栈的应用

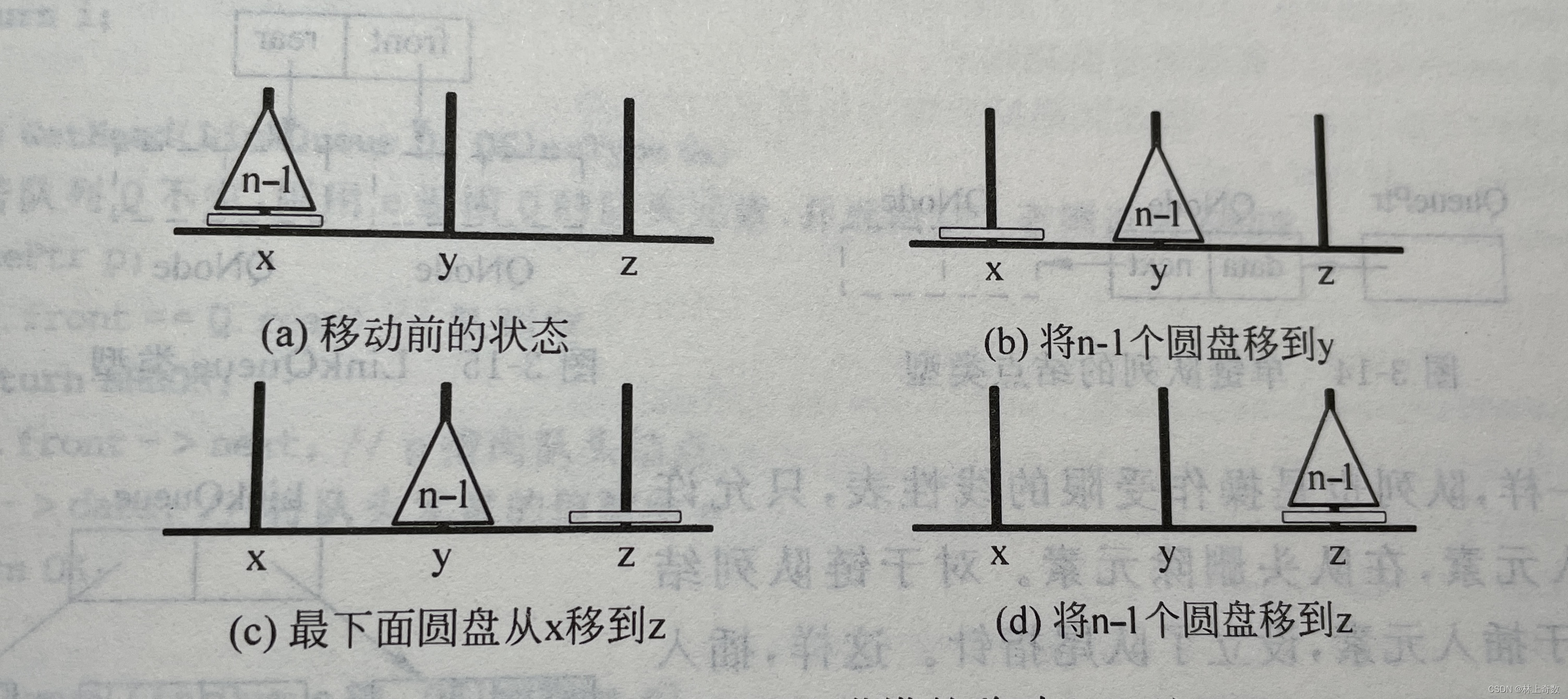
1，函数递归调用

函数递归调用时，计算机会把函数调用时需要的参数和返回地址等信息放入栈中，函数执行完毕后再从栈中取回这些信息。

//以汉诺塔问题为例展示栈的递归调用
#include <iostream>
 
int c = 0;
void move(char x,int n,char z){
    printf("第%i步:将%i号盘从%c移到%c\n", ++c, n, x, z);
}
 
void hanoi(int n, char x, char y, char z){
    if(n==1){
        move(x, 1, z);
    }
    else{
        hanoi(n-1, x, z, y);
        move(x, n, z);
        hanoi(n-1, y, x, z);
    }
}
 
int main() {
    int n;
    printf("三个塔座为a,b,c,圆盘最初在a座，借助b座移到c座，请输入圆盘数量：");
    scanf("%d",&n);
    hanoi(n, 'a', 'b', 'c');
}

2，表达式求值

在编译器中，中缀表达式转为后缀表达式后，可以使用栈来实现后缀表达式的求值。

char Precede(SElemType t1, SElemType t2)
{ 
  char f;
  switch(t2)
  { case '+':
    case '-': if(t1=='(' || t1=='\n')
                f='<'; 
              else
                f='>'; 
              break;
    case '*':
    case '/': if(t1=='*' || t1=='/' || t1==')')
                f='>'; 
              else
                f='<'; 
              break;
    case '(': if(t1==')')
              { printf("括号不匹配\n");
                exit(OVERFLOW);
              }
              else
                f='<'; 
              break;
    case ')': switch(t1)
              { case '(': f='='; 
                          break;
                case'\n': printf("缺乏左括号\n");
                          exit(OVERFLOW);
                default : f='>'; 
              }
              break;
    case'\n': switch(t1)
              { case'\n': f='='; 
                          break;
                case '(': printf("缺乏右括号\n");
                          exit(OVERFLOW);
                default : f='>'; 
              }
  }
  return f;
}
Status In(SElemType c)
{ 
  switch(c)
  { case '+':
    case '-':
    case '*':
    case '/':
    case '(':
    case ')':
    case'\n': return TRUE;
    default : return FALSE;
  }
}
SElemType Operate(SElemType a, SElemType theta, SElemType b)
{ 
  switch(theta)
  { case '+': return a+b;
    case '-': return a-b;
    case '*': return a*b;
  }
  return a/b; 
}
 
 
//  表达式求值（范围为int类型，输入负数要用（0-正数）表示）
typedef int SElemType; 
SElemType EvaluateExpression()
{ 
  SqStack OPTR, OPND;
  SElemType a, b, d, x; 
  char c; 
  c=getchar(); 
  InitStack(OPTR); 
  InitStack(OPND);
  Push(OPTR, '\n'); 
  GetTop(OPTR, x); 
  while(c!='\n' || x!='\n') 
  { if(In(c)) 
      switch(Precede(x, c)) 
      { case'<': Push(OPTR, c); 
                 c=getchar(); 
                 break;
        case'=': Pop(OPTR, x); 
                 c=getchar(); 
                 break;
        case'>': Pop(OPTR, x); 
                 Pop(OPND, b); 
                 Pop(OPND, a);
                 Push(OPND, Operate(a, x, b)); 
      }
    else if(c>='0' && c<='9') 
    { d=0;
      while(c>='0' && c<='9') 
      { d=d*10+c-'0';
        c=getchar();
      }
      Push(OPND, d); 
    }
    else 
    { printf("出现非法字符\n");
      DestroyStack(OPTR);
      DestroyStack(OPND);
      exit(OVERFLOW);
    }
    GetTop(OPTR, x); 
  }
  Pop(OPND, x); 
  if(!StackEmpty(OPND)) 
  { printf("表达式不正确\n");
    DestroyStack(OPTR);
    DestroyStack(OPND);
    exit(OVERFLOW);
  }
  DestroyStack(OPTR);
  DestroyStack(OPND);
  return x;
}
void main()
{
  printf("请输入算术表达式，负数要用（0-正数）表示\n");
  printf("%d\n", EvaluateExpression());
}

3，数制转换

可以使用栈来进行二进制和十进制等进制之间的转换

#define N 8 
typedef int SElemType; 
 
void conversion() 
{ 
  SqStack s;
  unsigned n; 
  SElemType e;
  InitStack(s); 
  printf("将十进制整数n转换为%d进制数，请输入：n（≥0）=", N);
  scanf("%u", &n); 
  while(n) 
  { Push(s, n%N); 
    n=n/N;
  }
  while(!StackEmpty(s)) 
  { Pop(s, e); 
    printf("%d", e); 
  }
  printf("\n");
}
void main()
{
  conversion();
}

4，迷宫求解

在迷宫求解中，可以使用栈来实现深度优先搜索算法。

// 利用栈求解迷宫问题（只输出一个解）
struct PosType 
{ int x; 
  int y; 
};
// 全局变量
PosType begin, end; 
PosType direc[4]={{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
// {行增量, 列增量}，移动方向依次为东南西北
#define MAXLENGTH 25 
typedef int MazeType[MAXLENGTH][MAXLENGTH]; 
MazeType m; 
int x, y; 
void Print()
{ 
  int i, j;
  for(i=0; i<x; i++)
  { for(j=0; j<y; j++)
      printf("%3d", m[i][j]);
    printf("\n");
  }
}
void Init()
{ 
  int i, j, x1, y1;
  printf("请输入迷宫的行数,列数（包括外墙）：");
  scanf("%d,%d", &x, &y);
 
  for(i=0; i<y; i++) 
  { m[0][i]=0; 
    m[x-1][i]=0; 
  }
  for(i=1; i<x-1; i++)
  { m[i][0]=0; 
    m[i][y-1]=0; 
  }
  for(i=1; i<x-1; i++)
    for(j=1; j<y-1; j++)
      m[i][j]=1; 
  printf("请输入迷宫内墙单元数：");
  scanf("%d", &j);
  printf("请依次输入迷宫内墙每个单元的行数,列数：\n");
  for(i=1; i<=j; i++)
  { scanf("%d,%d", &x1, &y1);
    m[x1][y1]=0; 
  }
  printf("迷宫结构如下：\n");
  Print();
  printf("请输入入口的行数,列数：");
  scanf("%d,%d", &begin.x, &begin.y);
  printf("请输入出口的行数,列数：");
  scanf("%d,%d", &end.x, &end.y);
}
int curstep=1; 
struct SElemType 
{ int ord; 
  PosType seat; 
  int di; 
};
 
 
// 定义墙元素值为0，可通过路径为1，经试探不可通过路径为-1，通过路径为足迹
Status Pass(PosType b)
{ 
  if(m[b.x][b.y]==1)
    return OK;
  else
    return ERROR;
}
void FootPrint(PosType b)
{ 
  m[b.x][b.y]=curstep;
}
void NextPos(PosType &b, int di)
{ 
 
  b.x+=direc[di].x;
  b.y+=direc[di].y;
}
void MarkPrint(PosType b)
{ 
  m[b.x][b.y]=-1;
}
Status MazePath(PosType start, PosType end) 
{ 
  
  PosType curpos=start; 
  SqStack S; 
  SElemType e; 
  InitStack(S); 
  do
  { if(Pass(curpos)) 
    { FootPrint(curpos); 
      e.ord=curstep; 
      e.seat=curpos; 
      e.di=0; 
      Push(S, e); 
      curstep++; 
      if(curpos.x==end.x && curpos.y==end.y) 
        return TRUE;
      NextPos(curpos, e.di); 
    }
    else 
    { if(!StackEmpty(S)) 
      { Pop(S, e); 
        curstep--; 
        while(e.di==3 && !StackEmpty(S)) 
        { MarkPrint(e.seat); 
          Pop(S, e); 
          curstep--; 
        }
        if(e.di<3) 
        { e.di++; 
          Push(S, e); 
          curstep++; 
          curpos=e.seat; 
          NextPos(curpos,e.di);
        }
      }
    }
  }while(!StackEmpty(S));
  return FALSE;
}
void main()
{
  Init(); 
  if(MazePath(begin, end)) 
  { printf("此迷宫从入口到出口的一条路径如下：\n");
    Print(); 
  }
  else
    printf("此迷宫没有从入口到出口的路径\n");
}

 

参考资料

1. 严蔚敏、吴伟民：《数据结构（C语言版）》
2. 高一凡：《数据结构算法解析》
3. 程杰：《大话数据结构》
4. 王道论坛：《数据结构考研复习指导》