7.卷积神经网络与计算机视觉

计算机视觉是一门研究如何使计算机识别图片的学科，也是深度学习的主要应用领域之一。

在众多深度模型中，卷积神经网络“独领风骚”，已经被称为计算机视觉的主要研究根据之一。

一、卷积神经网络的基本思想

卷积神经网络最初由 Yann LeCun（杨立昆）等人在1989年提出，是最初取得成功的深度神经网络之一。

1、局部连接

1、全局连接

传统的BP神经网络，例如多层感知器，前一层的某个节点与后一层的所有节点都有连接，后一层的某一个节点与前一层的所有节点也有连接，这种连接方式成为全局连接。

如果前一层有M个节点，后一层有N个节点，我们就会有 M×N 个链接权值，

每一轮反向传播更新权值的时候都要对这些权值进行重新计算，造成了 O（M×N）=O（n ²）的计算与内存开销。

2、局部连接

而局部连接的思想就是使得两层之间只有相邻的结点才进行连接，即连接都是“局部”的。

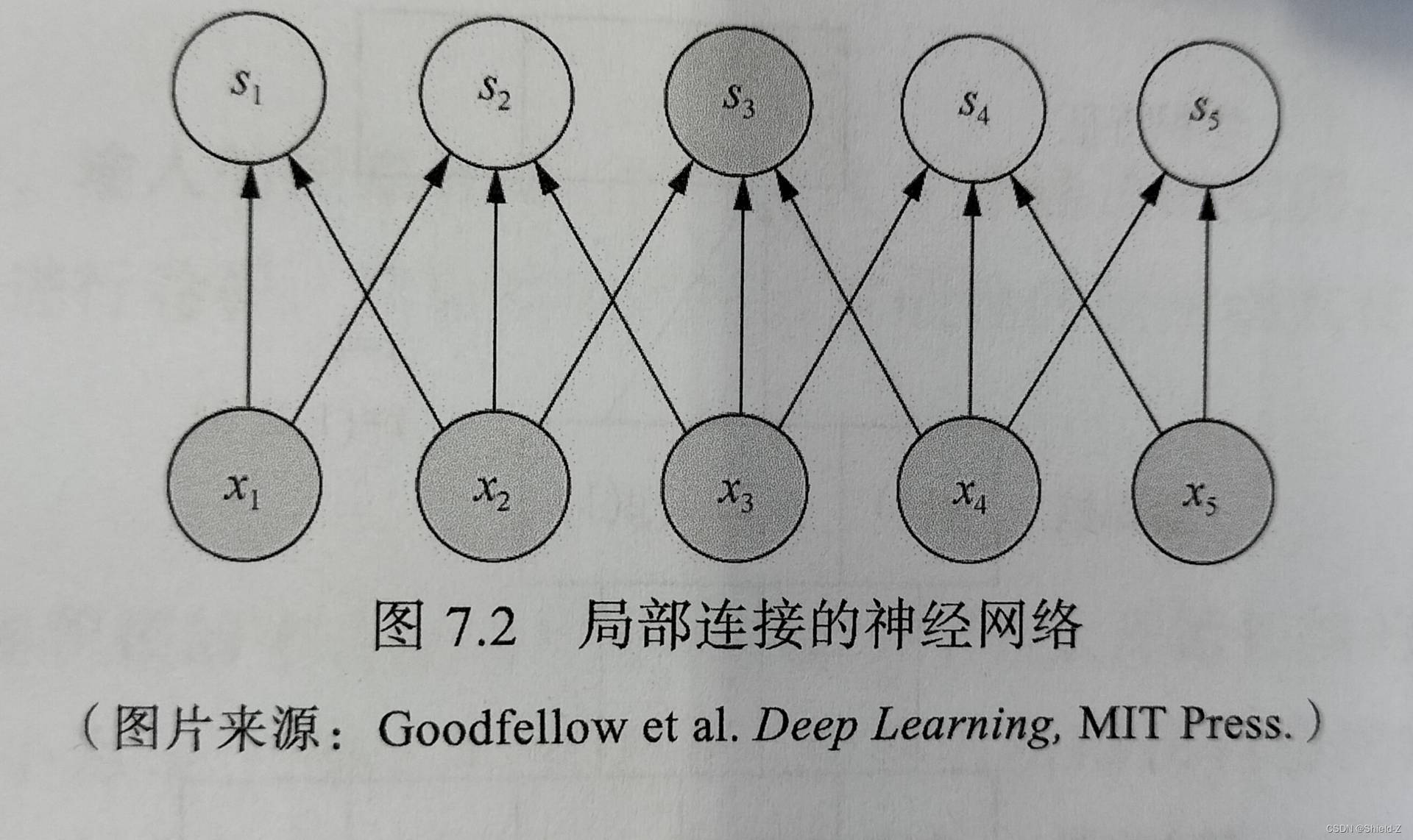
以图像处理为例，直觉上，图像的某一个局部的像素点组合在一起共同呈现出一些特征，而图像中距离比较远的像素点组合起来则没有什么实际意义，因此这种局部连接的方式可以在图像处理的问题上有较好的表现。

如果把连接限制在空间中相邻 c 个节点，就把连接权值降低到了 c×N，计算与内存开销就降低到了 O（c×N）= O（n） 。

2、参数共享

既然在图像处理中，我们认为图像的特征具有局部性，那么对于每一个局部使用不同的特征抽取方式（即不同的连续权值）是否合理？

由于不同的图像在结构上相差甚远，同一个局部位置的特征并不具有共性，对于某一个局部使用特定的连续权值不能让我们得到更好的结果。

因此我们考虑让空间中不同位置的结点连续权值进行共享，例如在局部连接的图中，属于结点 s₂的连续权值：

w = { w₁，w₂，w₃|w₁：x₁ → s₂；w₂：x₂ → s₂；w₃：x₃ →s₂}

可以被结点s₃ 以

w = { w₁，w₂，w₃|w₁：x₂ → s₃；w₂：x₃ → s₃；w₃：x₄ →s₃}

的方式共享。其他结点的权值共享类似。

这样一来，两层之间的连续权值就减少到 c 个。虽然在前向传播和反向传播的过程中，计算开销仍为 O（n），但内存开销被减少到常数级别O（c）。

二、卷积操作

离散的卷积操作正是这样一种操作，它满足了以上局部连接、参数共享的性质。代表卷积操作的结点层称为卷积层。

在泛函分析中，卷积被 f * g 定义为：

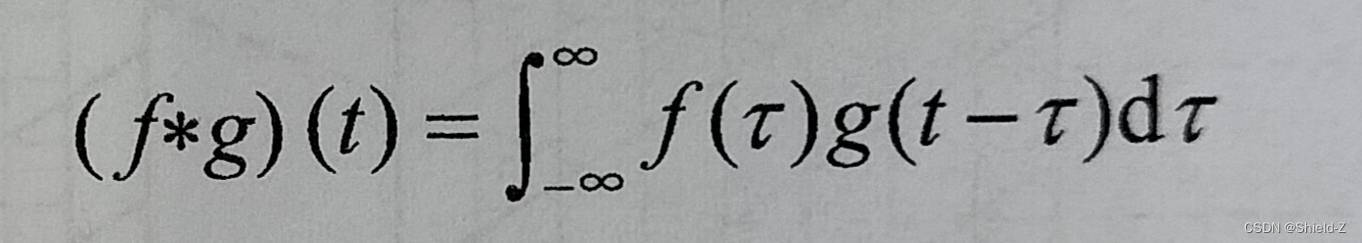
则一维离散的卷积操作可以被定义为：

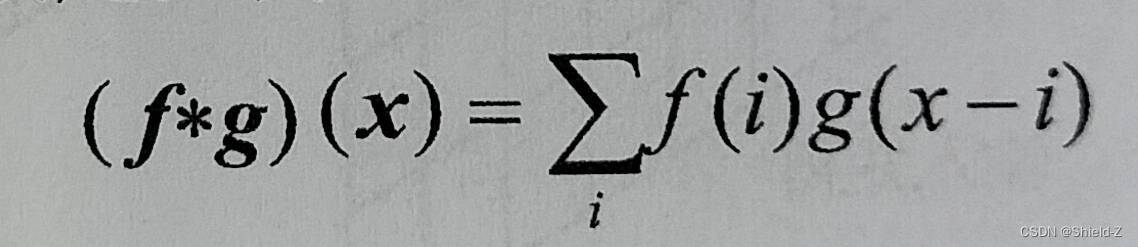
现在，假设 f 和 g 分别代表一个从向量下标到向量元素值的映射，令 f 表示输入向量，g 表示的向量称为卷积核（kermel），则卷积核施加于输入向量上的操作类似于一个权值向量在输入向量上移动，每移动一步进行一次加权求和操作；每一步移动的距离被称为步长（stride)。

例如，我们取输入向量大小为5，卷积核大小为3，步长为1，则卷积操作过程如图：

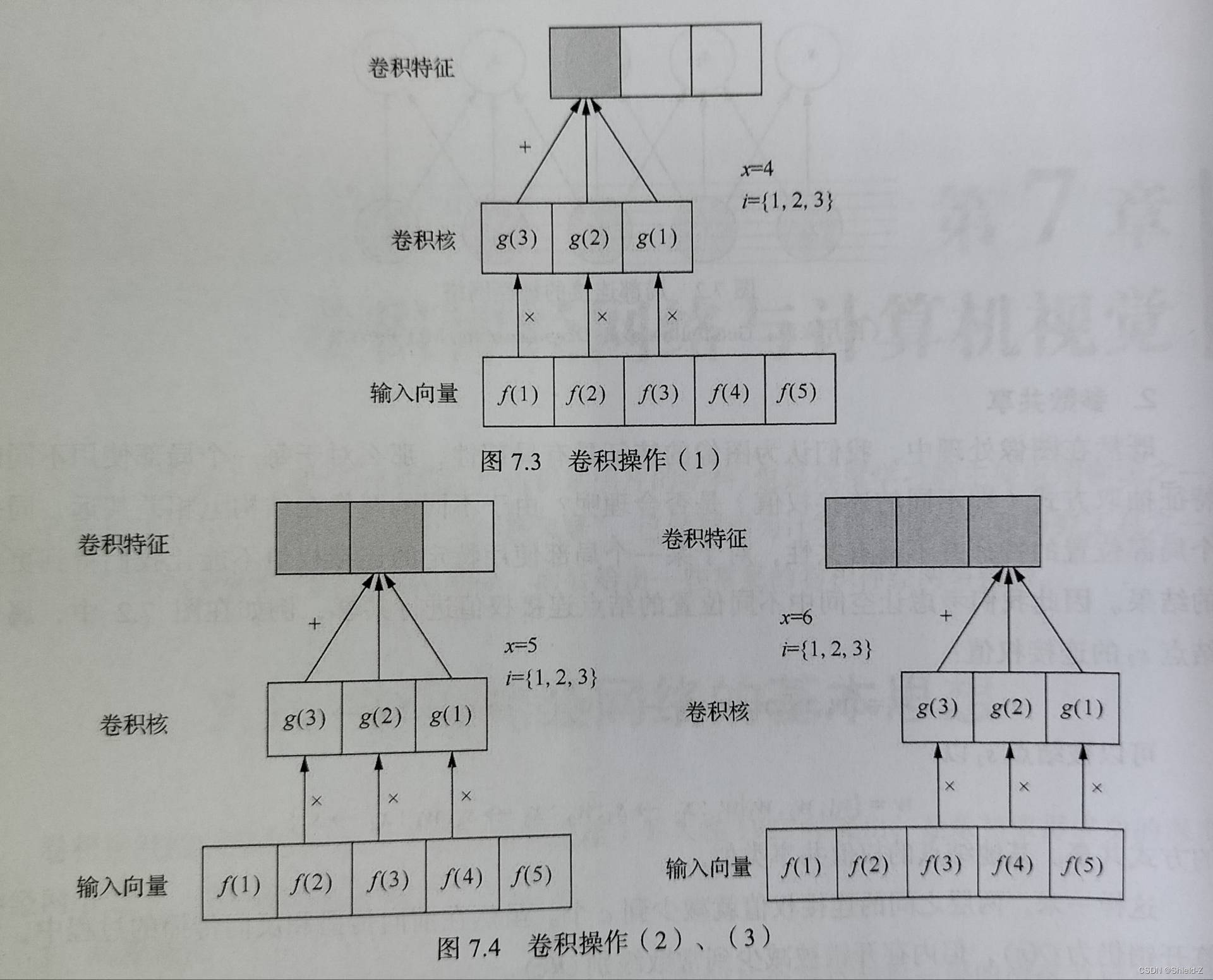
卷积核从输入向量左边开始扫描，权值在第一个位置分别与对应输入值相乘求和，得到卷积特征值向量的第一个值，接下来，移动1个步长，到达第二个位置，进行相同操作，依此类推。

这样就实现了从前一层的输入向量提取特征到后一层的操作，这种操作具有局部连接（每个结点只与其相邻的3个结点有连接）以及参数共享（所用的卷积核为同一个向量）的特征。

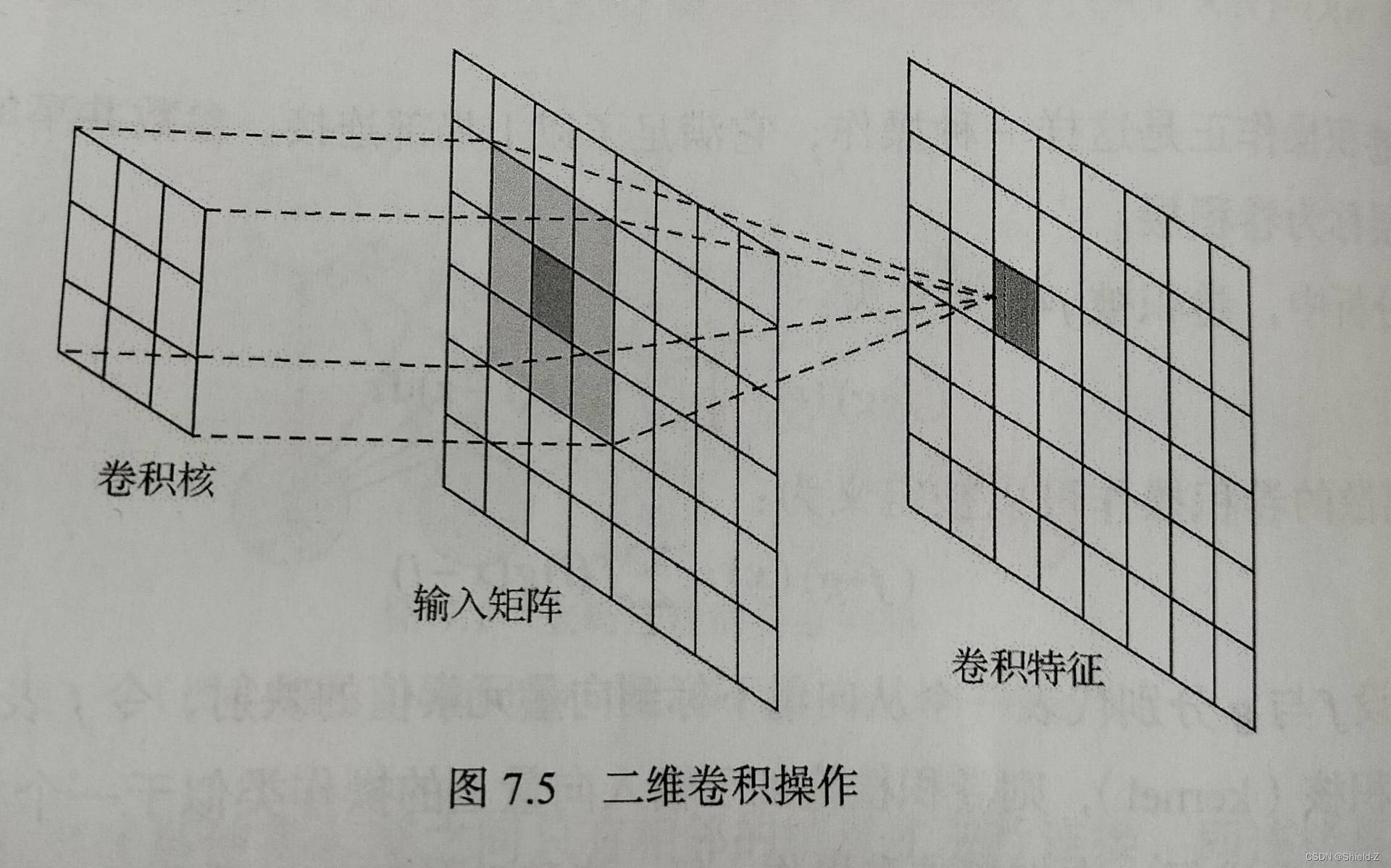
类似地，我们可以拓展到二维（如图）以及更高维度的卷积操作。

1、多个卷积核

利用一个卷积核进行卷积抽取特征是不充分的，因此在实践中，通常使用多个卷积核来提升特征提取的效果，之后将不同卷积核卷积所得的特征张量沿第一维拼接形成更高一个维度的特征张量。

2、多通道卷积

在处理彩色图像时，输入的图像有R、G、B这3个通道的数值，这个时候分别使用不同的卷积核对每一个通道进行卷积，然后使用线性或非线性的激活函数将相同位置的卷积特征合并为一个。

3、边界填充

注意在图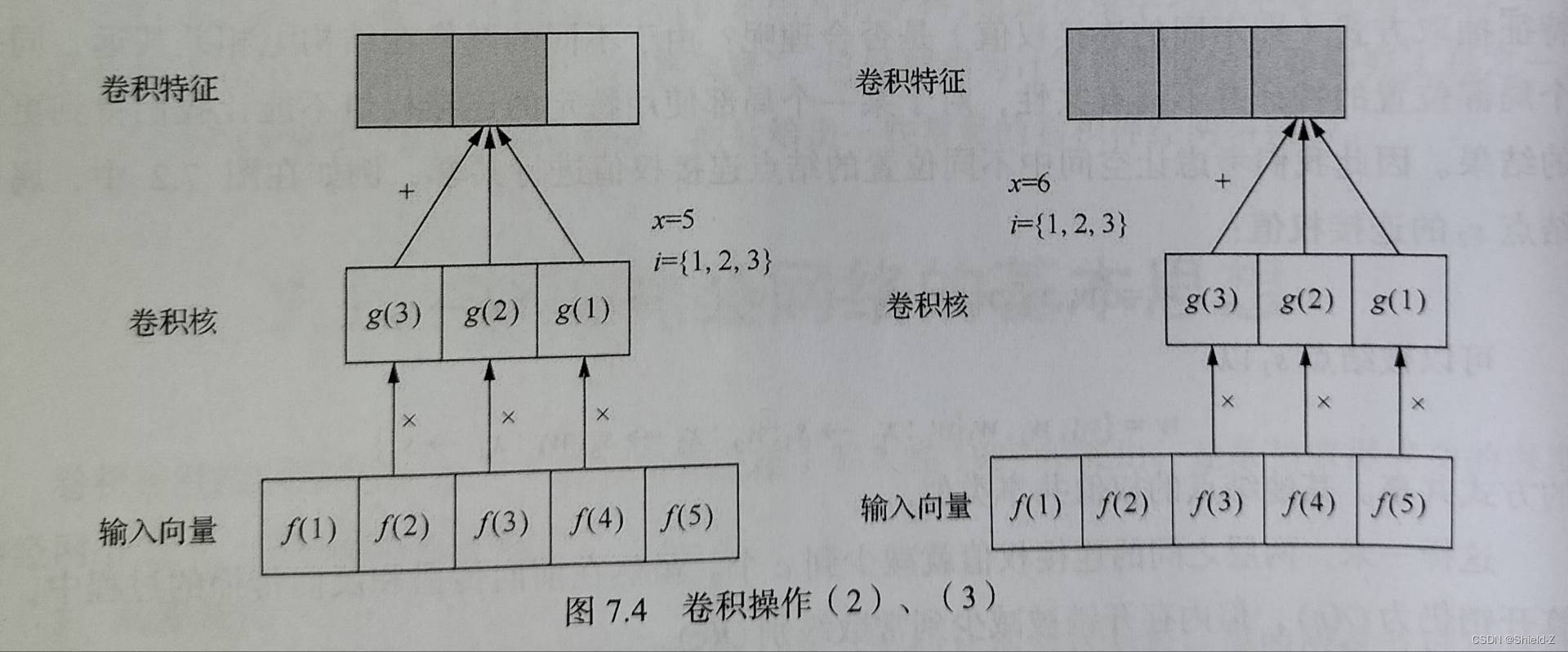中，卷积核的中心 g(2) 并不是从边界 f (1) 上开始扫描的。以一维

卷积为例，大小为 m 的卷积核在大小为 n 的输入向量上进行操作后所得的卷积特征向量大小会缩

小为 n-m+1。当卷积层数增加的时候，特征向量大小就会以 m-1的速度“坍缩”，这使得更深的神经网络变得不可能，因为在叠加到第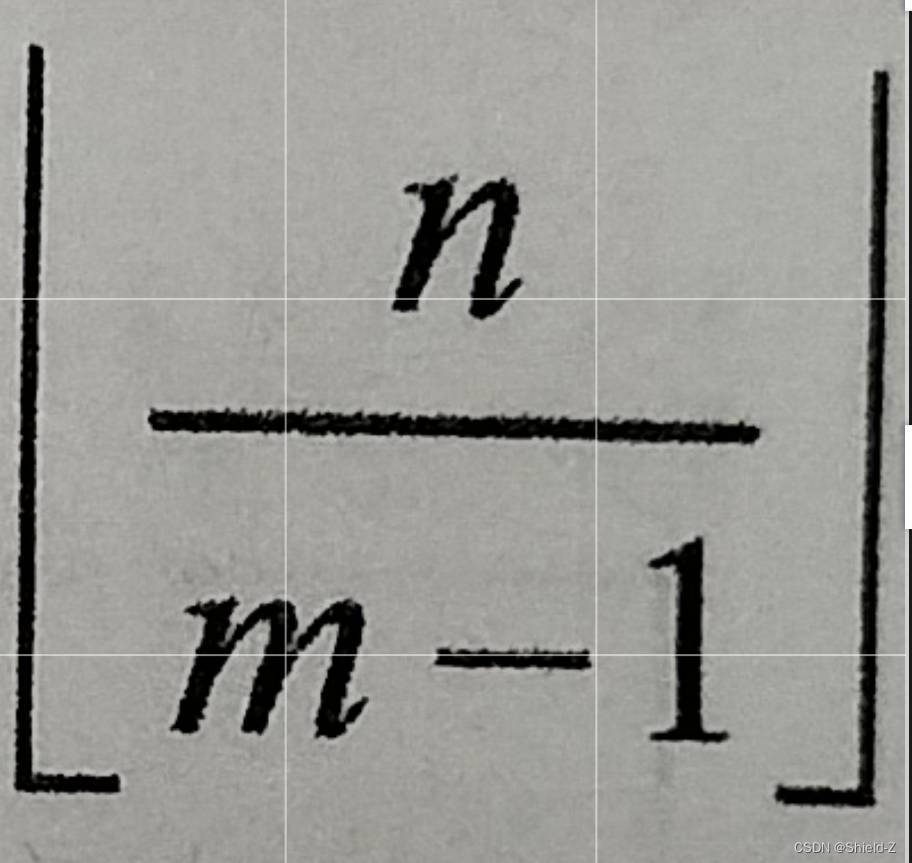个卷积层之后，卷积特征不足 m-1 维。

为了解决这一问题，人们通常采用在输入张量的边界上填充0的方式，使得卷积核的中心可以从边界上开始扫描，从而保持卷积操作输入张量和输出张量的大小不变。

三、池化层

池化（pooling，如下图）的目的是降低特征空间的维度，只抽取局部最显著的特征，同时这些特征出现的具体位置也被忽略。

这样做是符合直觉的：以图像处理维例，我们通常关注的是一个特征是否出现，而不太关心它们出现在哪里；这被称为图像的静态性。

通过池化降低空间维度的做法不但减少了计算开销，还使得卷积神经网络对于噪声具有健壮性。

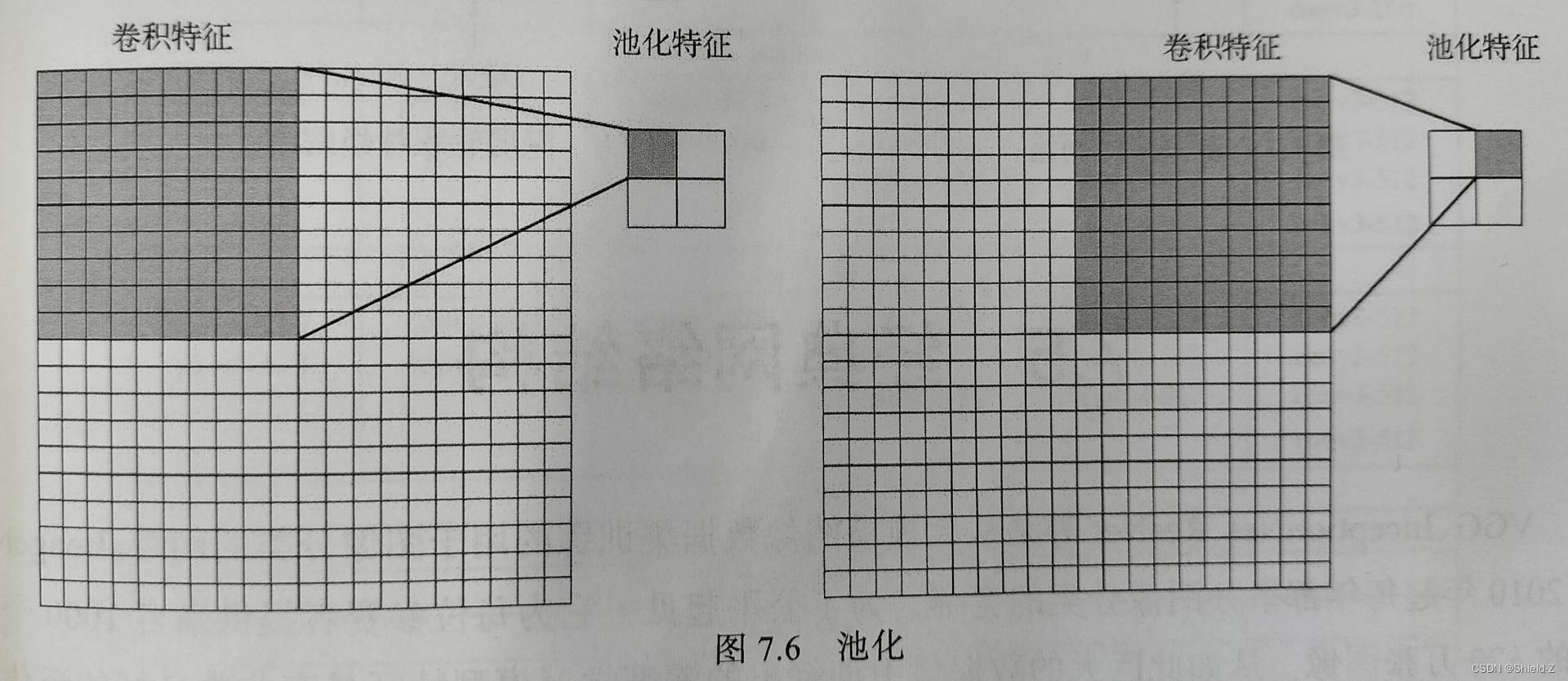
常见的池化类型有最大池化、平均池化等。

最大池化是指在池化区域中，取卷积特征值最大的作为所得池化特征值；

平均池化层是指在池化区域中，取所有卷积特征值的平均作为池化特征值。

如上图所示，在二维的卷积操作之后得到一个20×20的卷积特征矩阵，池化区域大小为10×10，这样得到的就是一个4×4的池化特征矩阵。

需要注意的是，与卷积核在重叠的区域进行卷积操作不同，池化区域是互不重叠的。

四、卷积神经网络

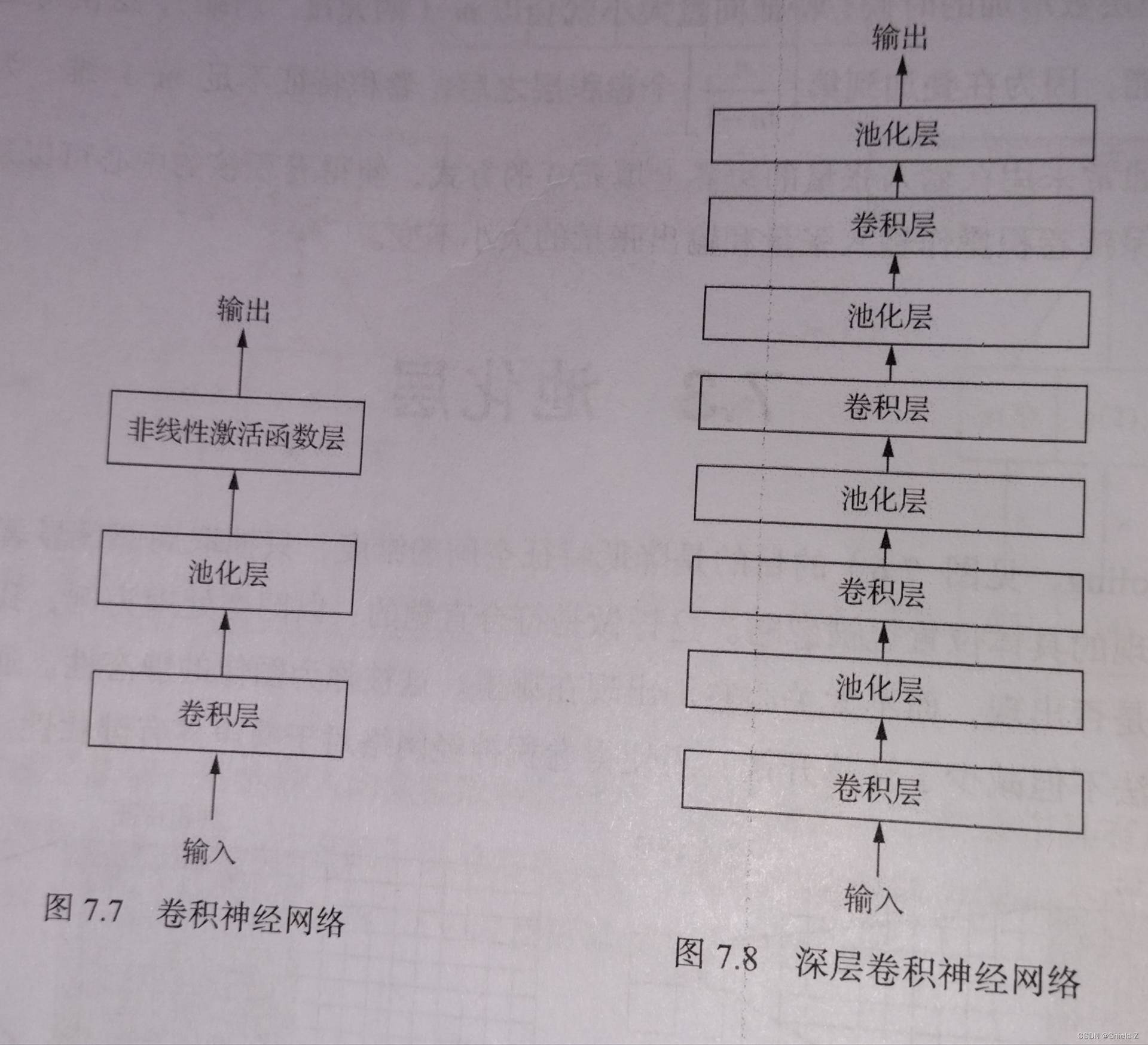
一般来说，卷积神经网络由卷积层、池化层、非线性激活函数层组成。如左下图：

在图像分类中表现良好的深度往往由许多“卷积层+池化层”的组合堆叠而成，通常多达数十乃至上百层。如右下图：

五、经典网络结构

VGG、InceptionNet、ResNet等是从大规模图像数据集训练的用于图像分类的网络。ImageNet从2010年起每年都举办图像分类的竞赛，为了公平起见，它为每位参赛者提供来自1000个类别的120万张图像。

从如此巨大的数据集后训练出的深度学习模型特征具有非常良好的泛化能力，在迁移学习后，它可以被用于除图像分类之外的其他任务，比如目标检测、图像分割等。

PyTorch 的 torchvision.models 为我们提供了大量的模型实现以及模型的预训练权重文件，其中就包括本节介绍的VGG、ResNet、InceptionNet。

1、VGG网络

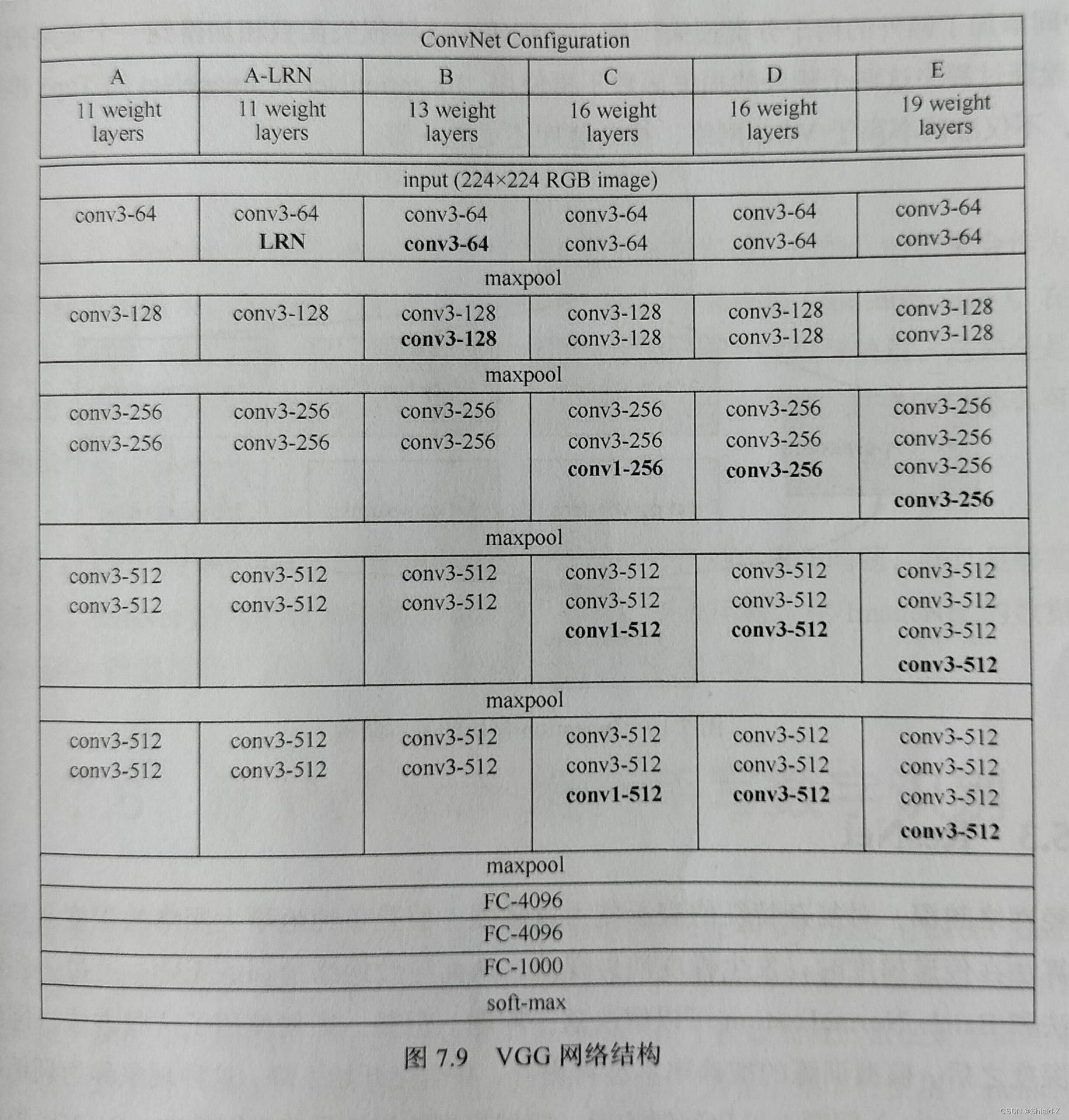
VGG网络的特点是用 3×3 的卷积核代替先前网络（如AlexNet）的大卷积核。

比如，3个步长为1的 3×3 的卷积核和一个 7×7 的卷积核的感受野（receptive field）是一致的，2个步长为1的 3×3 的卷积核和一个 5×5 的卷积核的感受野是一致的。

这样，感受野没有改变，但是却加深了网络的深度，提升了网络的拟合能力。

VGG网络的网络结构如图所示：

除此之外，VGG的全 3×3 的卷积核结构减少了参数量：

比如一个 7×7 的卷积核，其参数量为 7×7×C×C，而具有相同感受野的全 3×3 的卷积核的参数量为 3×3×3×C×C。

VGG网络和AlexNet的整体结构一致，都是先用5层卷积层提取图像特征，再用3层全连接层作为分类器。

【不过VGG网络的 “层” （在VGG中称为Stage）是由几个 3×3 的卷积层叠加起来的，

而AlexNet是1个大卷积层为一层。】

所以 AlexNet 只有8层，而VGG网络则可多达19层，VGG网络在 ImageNet 的 Top5 准确率达到了92.3%。VGG网络的主要问题是最后的3层全连接层的参数量过于庞大。

2、InceptionNet

InceptionNet（GoodLeNet）主要是由多个Inception模块实现的，Inception模块的基本结构如图所示：

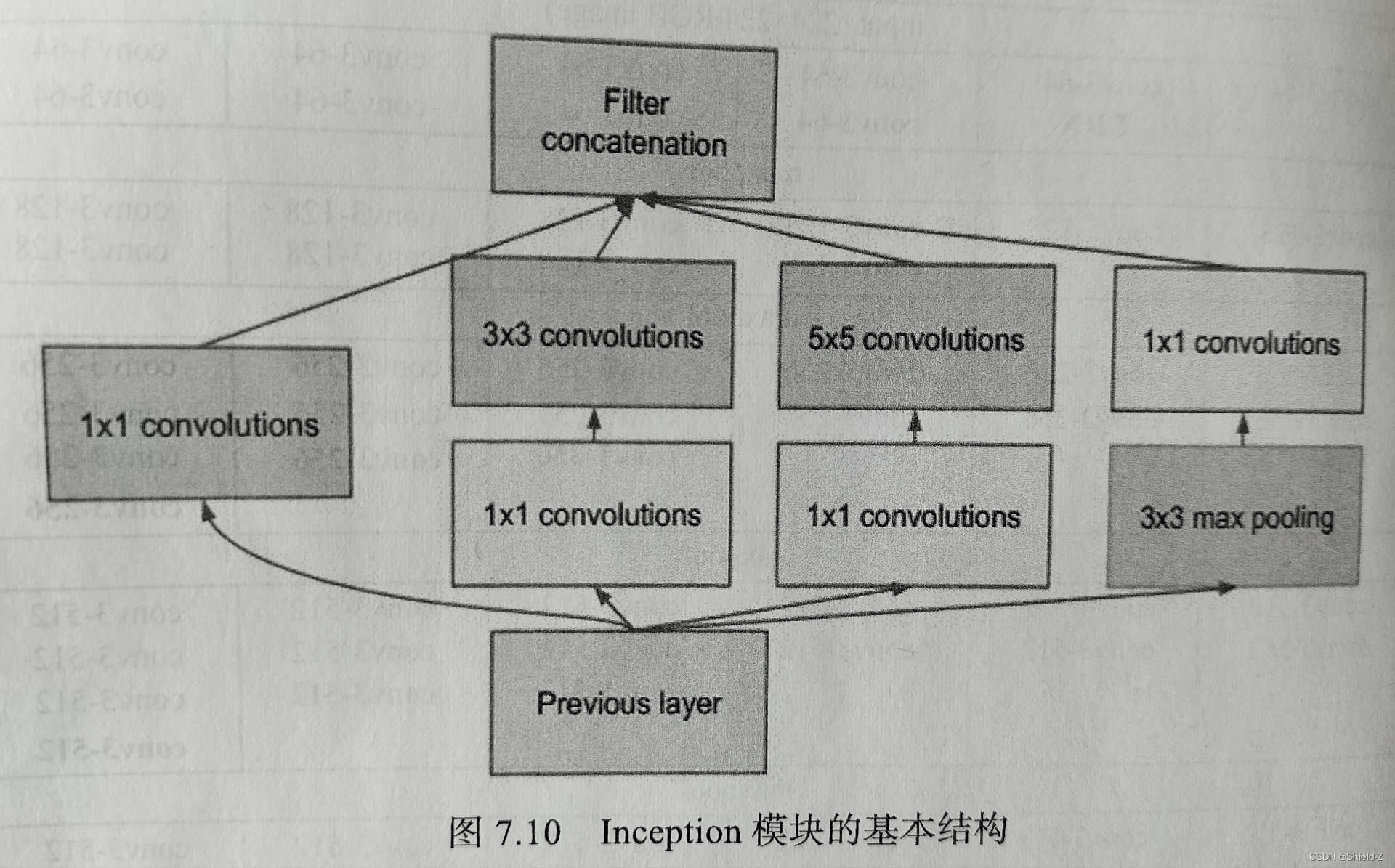
它是一个分支结构，一共有4个分支，

第1个分支是进行 1×1 卷积；

第2个分支是先进行 1×1 卷积，然后再进行 3×3 卷积；

第3个分支同样先进行 1×1 卷积，然后再进行 5×5 卷积；

第4个分支先进行 3×3 的最大池化，然后再进行 1×1 卷积。

最后，4个分支计算过的特征映射用沿通道维度拼接的方式组合到一起。

图中的中间层可以分为4列来看，其中第1列的 1×1 的卷积核和中间两列的 3×3、5×5的卷积核主要用于提取特征。

不同大小的卷积核拼接到一起，使得这一结构具有多尺度的表达能力。

右侧3列的1×1的卷积核用于特征降维，可以减少计算量。

第4列最大池化层的使用是因为实验表明池化层往往有比较好的效果。

这样设计的Inception模块具有相当大的宽度，计算量却更低。前面提到了VGG的主要问题是最后3层全连接层参数量过于庞大，在InceptionNet中弃用了这一结构，取而代之的是一层全局平均池化层和单层的全连接层。

这样减少了参数量并且加快了模型的推断速度。

最后，InceptionNet达到了22层，为了让深度如此大的网络能够稳定地训练，Inception在网络中间添加了额外的两个分类损失函数，在训练中这些损失函数相加得到一个最终的损失函数，在验证过程中这两个额外的损失函数不再使用。InceptionNet 在 ImageNet 的 Top5准确率为93.3%，不仅准确率高于VGG网络，推断速度还更甚一筹。

3、ResNet

神经网络越深，对复杂特征的表示能力就越强。但是单纯地增大网络的深度会导致当反向传播算法在传递梯度时，发生梯度消失现象，从而导致网络的训练无效。通过一些权重初始化方法和 Batch Normalization可以解决这一问题。

但是，即使使用了这些方法，网络在达到一定深度之后，模型训练的准确率不会再提升，甚至会开始下降，这种现象称为训练准确率的退化（degradation）问题。

退化问题表明，深层模型的训练是非常困难的。

ResNet提出了残差学习的方法，用于解决深度学习模型的退化问题。

假设输入数据是 x ，常规的神经网络是通过几个堆叠的层去学习映射 H（x），而ResNet学习的是映射和输入的残差 F（x）= H（x）- x。

相应地，原有的表示就变成 H（x）= F（x）+ x。

尽管两种表示是等价的，但实验表明，残差学习更容易训练。ResNet是由几个堆叠的残差模块表示的，可以将残差结构形式化为：

y = F（x，{W} ）+ x

其中 F（x，{W} ）表示要学习的残差映射，ResNet的基本结构如图所示：

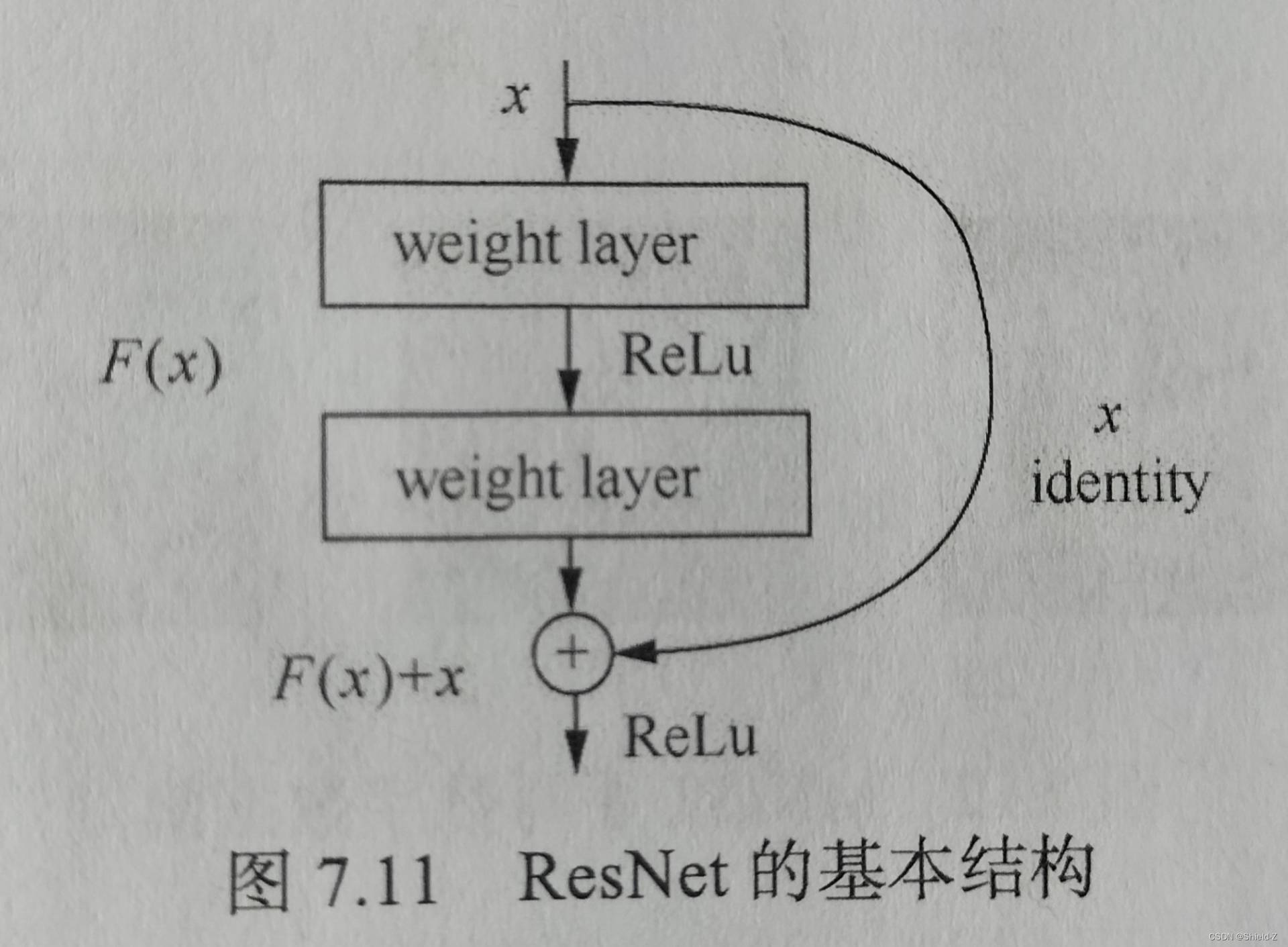
图中，残差映射一共有两层，可表示为 y = W₂δ（W₁x + b₁）+ b₂ 。

其中 δ 表示 ReLU激活函数。

图中例子一共有两层，ResNet的实现中大量采用了两层或三层的残差结构，而实际这个数量并没有限制，当它仅为一层时，残差结构就相当于一个线性层，所以就没有必要采用单层的残差结构了。

F（x）+ x 在ResNet中通过 shortcut 连接和逐元素相加实现，相加后的结果会作为下一个ReLU激活函数的输入。

shortcut 连接相当于对输入x进行恒等映射（indentity map）。在非常极端的情况下，残差F（x）会等于0，而使得整个残差模块仅进行一次恒等映射，这完全是由网络自主决定的，只要它自身认为这是更好的选择。

如果 F（x）和 x 的维度并不相同，那么可以采用如下结构使得其维度相同：

y = F（x，{W}）+ {W} x  。

但是，ResNet的实验表明，使用恒等映射就能够很好地解决退化问题，并且足够简单，计算量足够小。

ResNet的残差结构解决了深度学习模型的退化问题，在ImageNet的数据集上，最深的ResNet模型达到了152层，其Top5准确率达到了95.51%。

六、用PyTorch进行手写数字识别  

torch.utils.data.Datasets 是PyTorch用来表示数据集的类，在本节我们使用 torchvision.datasets.MNIST 构建手写数字数据集。

实例化 datasets对象：

datasets.MNIST能够自动下载数据并保存到本地磁盘，参数train默认为True，用于控制加载的数据集是训练集函数测试集。

使用 len（mnnist），这里调用__len__方法。

使用mnist [ j ] ，调用的是__getitem__。

绘制MNIST手写数字数据集

当我们自己建立数据集时，需要继承Dataset，并且覆写__item__和__len__两个方法。

数据预处理是非常重要的步骤，PyTorch提供了 torchvision.transforms，可用于处理数据及实现数据增强。

在这里我们使用了transforms.ToTensor，它将 PIL Image 或者 numpy.ndarray 类型的数据转换为 Tensor ，并且它会将数据从 [0,255] 映射到 [0,1]。

transforms.Normalize会将数据标准化，将训练数据标准化会加速模型在训练中的收敛。

在使用中，可以利用torchvision.transforms.Compose将多个transforms组合到一起，被包含的transforms会顺序执行。

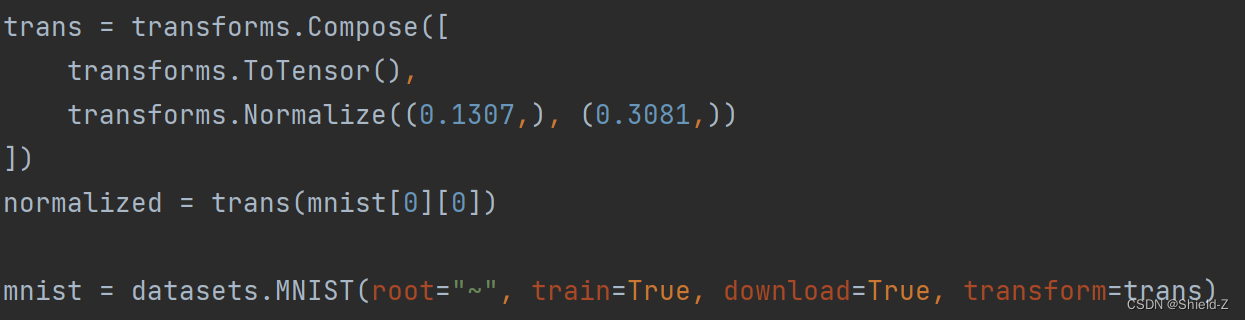
准备好处理数据的流程后，就可以读取用于训练的数据了，torch.utils.data.DataLoader提供了迭代数据、随机抽取数据、批处理数据、使用multiprocrssing并行化读取数据的功能。

下面定义了函数 imshow ；将数据从标准化的数据中恢复出来；将数据从Tensor类型转换为 ndarray，这样才可以用Matplotlib绘制出来。

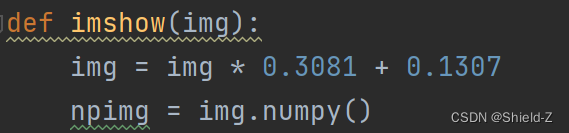
将矩阵的维度从 (C,W,H）转化为（W,H,C）。注：C、W、H属于通用符，分别表示 channel、weight、height。

前面展示了使用PyTorch加载数据，处理数据的方法。

下面我们构建用于识别手写数字的神经网络模型。

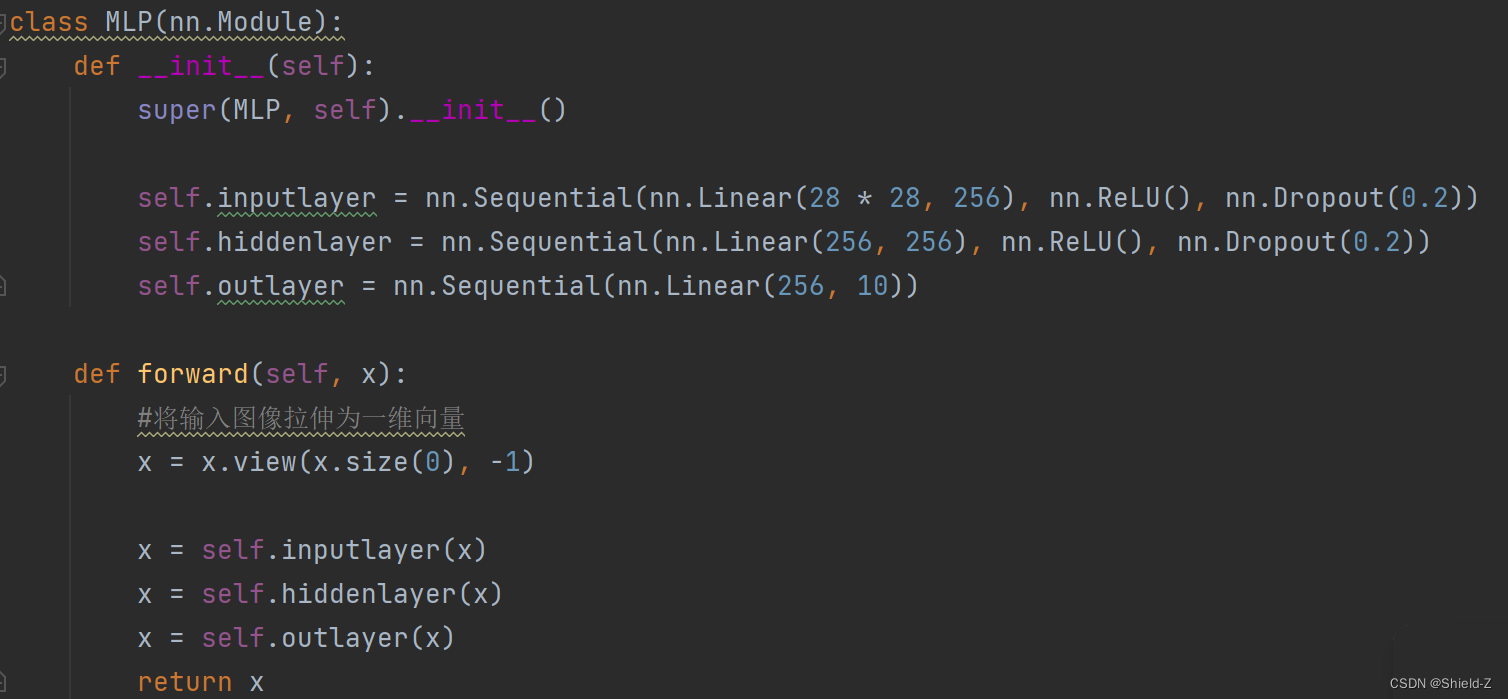
我们可以直接通过输出nn.Module的对象看到其网络结构

在准备好数据和模型后，我们就可以训练模型了。

下面我们分别定义数据处理和加载流程、模型、优化器、损失函数，以及用准确率评估模型能力。

from torch import optim
from tqdm import tqdm
#数据处理和加载
trans = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.1307,),(0.3081,))])
mnist_train = datasets.MNIST(root="~",train=True,download=True,transform=trans)
mnist_val = datasets.MNIST(root="~",train=False,download=True,transform=trans)
 
trainloader = DataLoader(mnist_train, batch_size=16, shuffle=True,num_workers=4)
valloader   = DataLoader(mnist_val, batch_size=16, shuffle=True,num_workers=4)
 
#模型
model = MLP()
 
#优化器
optimizer = optim.SGD(model.parameters(),lr=0.01,momentum=0.9)
 
#损失函数
celoss = nn.CrossEntropyLoss()
best_acc = 0
 
#计算准确率
def accuracy(pred,target):
    pred_label = torch.argmax(pred,1)
    correct = sum(pred_label == target).to(torch.float)
    #acc = correct/float(len(pred))
    return correct,len(pred)
 
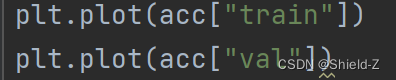
acc = {"train":[],"val":[]}
loss_all = {"train":[],"val":[]}
 
for epoch in tqdm(range(10)):
    #设置为验证模式
    model.eval()
    numer_val,denumer_val,loss_tr = 0.,0.,0.
    with torch.no_grad():
        for data,target in valloader:
            output = model(data)
            loss = celoss(output,target)
            loss_tr +=loss.data
 
            num,denum = accuracy(output,target)
            numer_val += num
            denumer_val += denum
        #设置为训练模式
        model.train()
        numer_tr,denumer_tr,loss_val = 0.,0.,0.
        for data,target in trainloader:
            optimizer.zero_grad()
            output = model(data)
            loss = celoss(output,target)
            loss_val += loss.data
            loss.backward()
            optimizer.step()
            num,denum = accuracy(output,target)
            numer_tr +=num
            denumer_tr += denum
        loss_all["train"].append(loss_tr/len(trainloader))
        loss_all["val"].append(loss_val/len(trainloader))
        acc["train"].append(numer_tr/denumer_tr)
        acc["val"].append(numer_val/denumer_val)

将训练数据迭代10个轮次（epoch），并将训练和验证的准确率和损失记录下来。

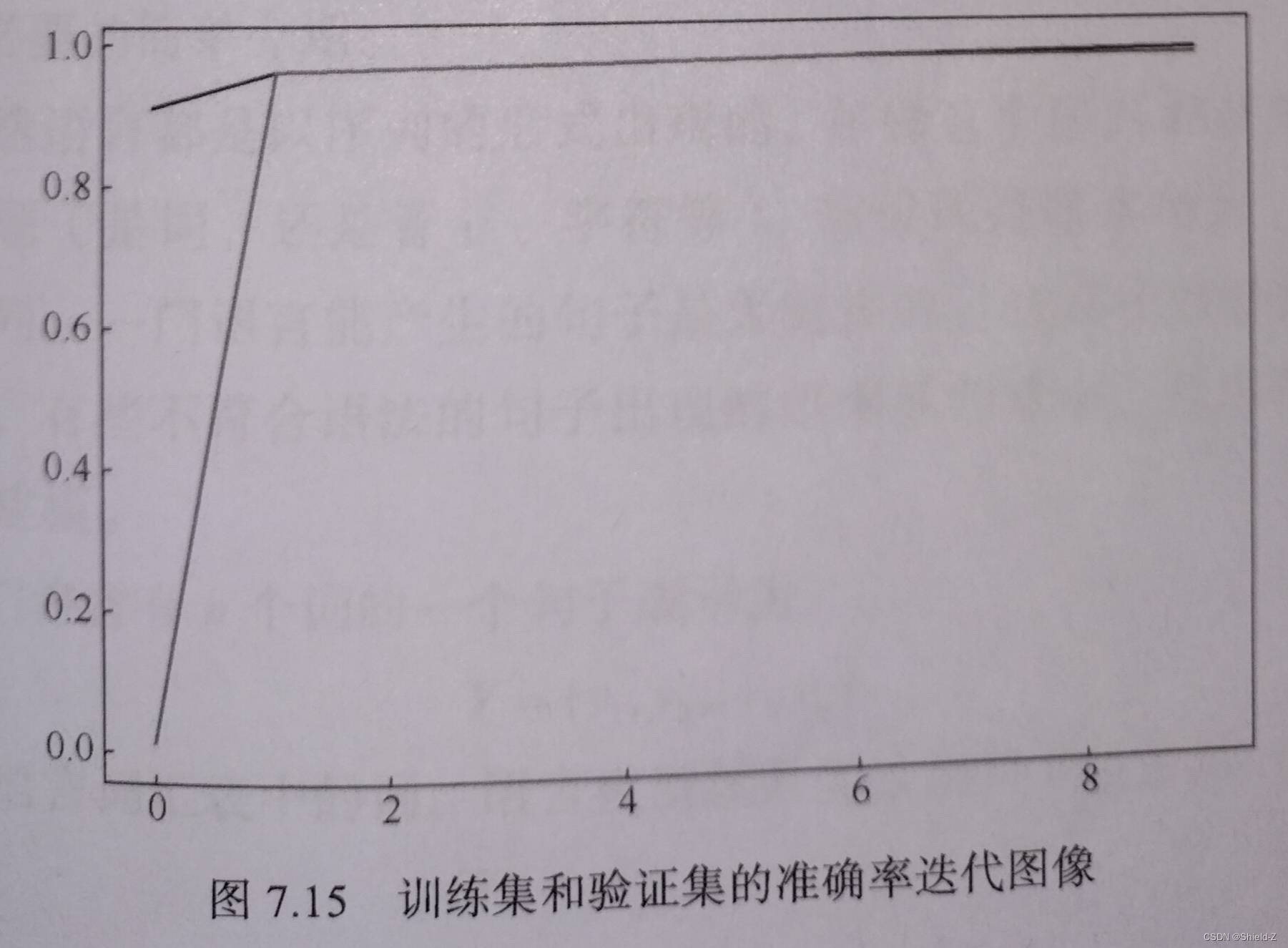
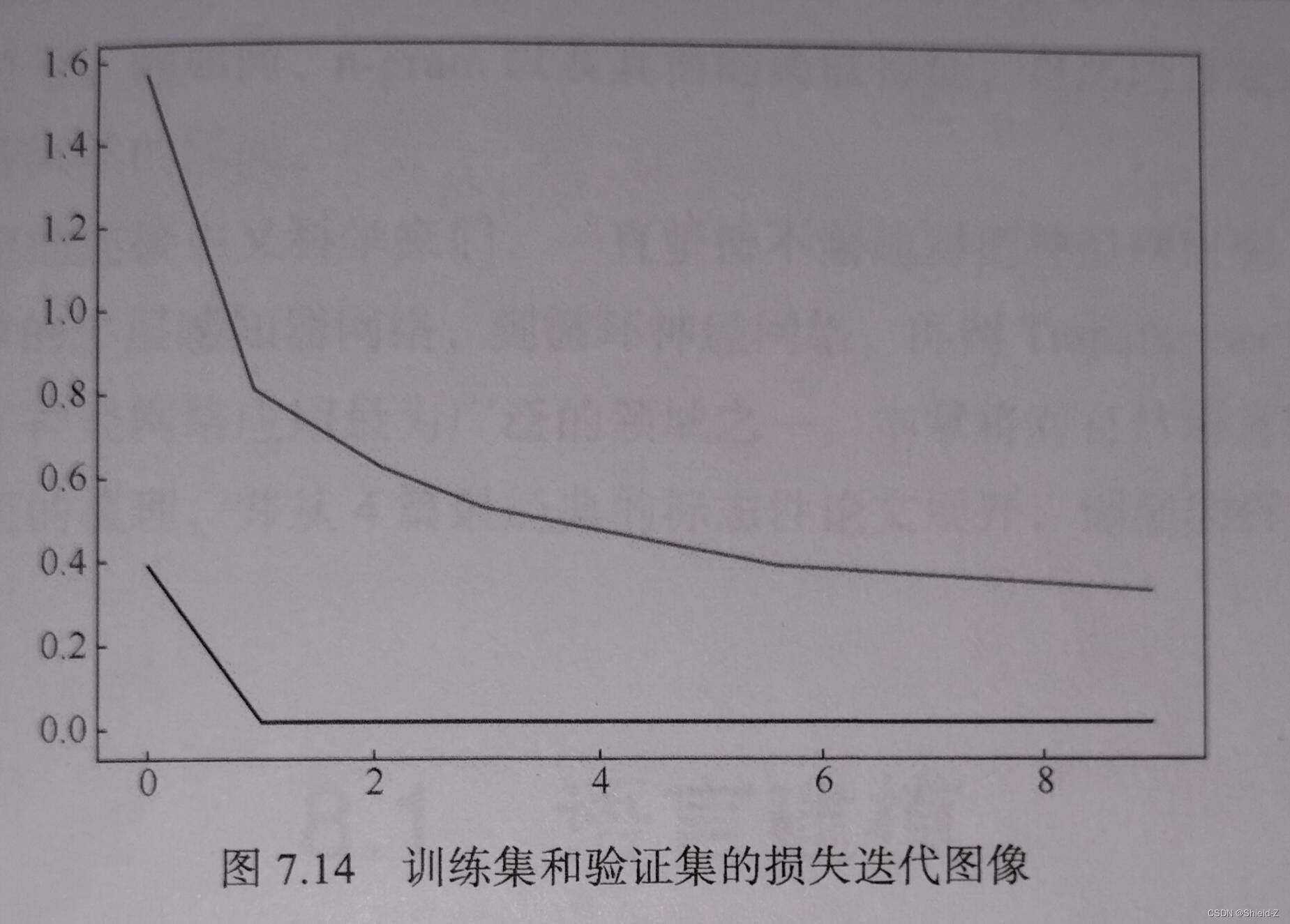
模型训练迭代后，训练集和验证集的损失迭代图像如图：

模型训练迭代后，训练集和验证集的准确率迭代图如图：