自然语言处理之循环神经网络_自然语言处理与循环神经网络

1. RNN基础

  循环神经网络RNN,是一类用于处理序列数据的神经网络。就像卷积网络是专门用于处理网格化数据的神经网络，循环神经网络是专门用于处理序列$x^{(1)},\dots ,x^T$的神经网络。正如卷积网络可以很容易地扩展到具有很大宽度的高度的图像，以及处理大小可变的图像，循环网络可以扩展到更长的序列，大多数循环网络也能处理可变长的序列。

1.1 RNN的结构

  其中每个圆圈可以看作是一个单元，而且每个单元做的事情也是一样的，因此可以折叠呈左半图的样子。用一句话解释RNN，就是一个单元结构重复使用。

• $x_t$ 是时间t处的输入 ;
• $s_t$是时间t处的“记忆”，$s_t=f(U(X_t)+W\cdot s_{t-1})$，f可以是tanh等 ;
• $o_t$是时间t出的输出，比如是预测下个词的话，可能是softmax输出的属于每个候选词的概率

  循环神经网络在t时刻接收到输入$x_t$之后，隐藏层的值是$s_t$，输出值是$o_t$。关键一点是，st的值不仅仅取决于$x_t$，还取决于$s_{t-1}$。我们可以用下面的公式来表示循环神经网络的计算方法：
$$s_t=f(U(x_t)+W\cdot s_{t-1})$$ $$o_t=g(V{s}_t)$$
  式2是输出层的计算公式，输出层是一个全连接层，也就是它的每个节点都和隐藏层的每个节点相连。V是输出层的权重矩阵，g是激活函数。式2是隐藏层的计算公式，它是循环层。U是输入x的权重矩阵，W是上一次的值作为这一次的输入的权重矩阵，f是激活函数。

  循环神经网络也是由输入层、隐藏层、输出层构成的。区别之处在于隐藏层的输出会存储到记忆单元中。记忆单元会和输入层同时作为下个输入。

  为了更好理解网络的内部结构，下图为网络结构图(包括了)，其中词向量维度为4，隐藏层神经元为单层，隐藏层神经元个数为3，输出维度为4。如果和MLP进行对比的话，考虑了单词之间的顺序，对于每一步来说，隐藏层多了当前时刻的输入以及上一时刻的隐藏层。

  个人浅显理解：我们看看第一个隐层表示的是第一个词内部关系，第二个隐层表示的是第二个词和第一个词之间的关系，第三个隐层输出的是第三个词和(第二个词和第一个词之间的关系)的关系，举个例子，如：abc为一句话，第二个隐层能够表示b和a的关系，第三个隐层的输出能够表示c和b，a之间的关系。那么黑色连接部分是表示关系转换信息，也就是ab和abc之间应该存在着某些特定的模式，而转换矩阵w就是要学习到这些关系；蓝色的连接是当前词对当前句子的影响程度；绿色连接和黑色连接的意义差不多。

  通过图我们也可以看出RNN的巧妙之处，对于任意长度的输入，输出是一致的；能够表达序列之间的关系；参数共享易于训练。但是也发现了一个问题，就是RNN对于长句子表达的不好，我们看到第一个词和最后一个词的关系是通过好多次转换矩阵才产生的，这样句子很长这种关系就很难表示出来，这也一度成为RNN的瓶颈，当然这些问题最后被LSTM（1997），GRU等RNN变种网络给解决了。一个有趣的问题是，类似于LSTM这种直接连接近似解决梯度弥散的方法在CNN使用中直到ResNet（2015）提出才被广泛使用，不过两者相差了好多年，也充分说明了一个现象，只有想不到没有做不到，哈哈。

  接下来我们再看看模型的容量，如词向量的维度是1024维，隐层有1000个单元，输出也是1024维，那么整个网络的参数个数为：U参数+V参数+W参数=10241000+10001024+10001000≈310^6，也就是300万个参数，这个模型的容量对于千变万化的语言来说估计有点小。

  但在使用tensorflow.keras和Pytorch中，RNN或者LSTM本质上只包括上图中的输入层和隐藏层，而输出层是需要自己添加，如全连接层。

  为了更好的理解RNN，我们举例来说，其中词向量维度为1，隐藏层神经元个数为1，如下图所示：

  要得到$y_1$和$y_2$，分为两步，分别是：

1. 更新hidden layer，其中hidden layer更新的时候，有四个输入(given initial value1、given initial value2、$x_1$、$x_2$)。
2. 更新output layer($y$)，有2个输入，分别是两个隐藏层的神经元。
   
     其中最下方黄色的块指的是输入层（输入分别为[1, 1], [1, 1], [2, 2]）。中间绿色的块指的是隐藏层（隐藏层的初始值为[0, 0]），橘红色指的是输出层。蓝色指的是记忆单元（上一次隐藏层的结果）。此时输入（最下层的黑色线）和记忆单元（蓝色线）会共同输入，从而计算出本次隐藏层的结果。然后两个隐藏单元的结果汇总得到输出$y_1$和$y_2$。
   
     然后把[2, 2]放进记忆单元，如下图所示：
   
     新的输入[1, 1]，记忆单元为[2, 2]，隐藏层单个结果即为1+1+2+2 = 6，$y_1$即为6+6=12，如下图所示：
   
     然后把[6, 6]放进记忆单元，如下图所示：
   
     新的输入[2, 2]，记忆单元为[6, 6]，隐藏层单个结果即为2+2+6+6 = 16，$y_1$即为16+16=32，如下图所示：
   

1.2 循环神经网络的提出背景

  RNN通过每层之间节点的连接结构来记忆之前的信息，并利用这些信息来影响后面节点的输出。RNN可充分挖掘序列数据中的时序信息以及语义信息，这种在处理时序数据时比全连接神经网络和CNN更具有深度表达能力，RNN已广泛应用于语音识别、语言模型、机器翻译、时序分析等各个领域。

1.3 BPTT算法

• RNN的训练方法——BPTT算法（back-propagation through time）
    BPTT（back-propagation through time）算法是常用的训练RNN的方法，其实本质还是BP算法，只不过RNN处理时间序列数据，所以要基于时间反向传播，故叫随时间反向传播。BPTT的中心思想和BP算法相同，沿着需要优化的参数的负梯度方向不断寻找更优的点直至收敛。综上所述，BPTT算法本质还是BP算法，BP算法本质还是梯度下降法，那么求各个参数的梯度便成了此算法的核心。 这里寻优的参数有三个，分别是U、V、W。与BP算法不同的是，其中W和U两个参数的寻优过程需要追溯之前的历史数据，参数V相对简单只需关注目前，那么我们就来先求解参数V的偏导数。
  $$\frac{\partial L^{(t)}}{\partial V}=\frac{\partial L^{(t)}}{\partial o^{(t)}}\cdot \frac{\partial o^{(t)}}{\partial V}$$
    这个式子看起来简单但是求解起来很容易出错，因为其中嵌套着激活函数函数，是复合函数的求导过程。RNN的损失也是会随着时间累加的，所以不能只求t时刻的偏导。W和U的偏导的求解由于需要涉及到历史数据，其偏导求起来相对复杂，我们先假设只有三个时刻，那么在第三个时刻 L对W的偏导数为：
  $$L=\sum _{n=1}^n{L}^{(t)}$$
  $$\frac{\partial L}{\partial V}=\sum _{n=1}^n\frac{\partial L^{(t)}}{\partial o^{(t)}}\cdot \frac{\partial o^{(t)}}{\partial V}$$

2. 双向RNN

  Bidirectional RNN(双向RNN)假设当前t的输出不仅仅和之前的序列有关，并且 还与之后的序列有关，例如：预测一个语句中缺失的词语那么需要根据上下文进 行预测；Bidirectional RNN是一个相对简单的RNNs，由两个RNNs上下叠加在 一起组成。输出由这两个RNNs的隐藏层的状态决定。双向RNN相当于并联结构，而多层RNN相当于串联结构。

3. 递归神经网络

  在RNN中，信息只在一个方向上移动。当它作出决定时，会考虑当前的输入以及它从之前收到的输入中学到的内容。下面的两张图片说明了RNN和前馈神经网络之间的信息流的差异。

  通常RNN是具有短期记忆的，结合LSTM，他们也有长期记忆，这一点，我们将在下面进一步讨论。

  说明RNN记忆概念的另一个好方法是用一个例子来解释它：假设你有一个正常的前馈神经网络，并给它一个单词“neuron(神经元)”作为输入，并逐字处理这个单词。当它到达字符“r”时，它已经忘记了“n”，“e”和“u”，这使得这种类型的神经网络几乎不可能预测接下来会出现什么字符。而经常性的神经网络则能够准确记住，因为它是内部记忆。它产生输出，复制输出并将其循环回网络。递归神经网络有两个输入，现在和最近的过去。这很重要，因为数据序列包含关于接下来会发生什么的重要信息，这就是为什么RNN可以做其他算法无法做的事情。与所有其他深度学习算法一样，前馈神经网络将权重矩阵分配给其输入，然后生成输出。请注意，RNN将权重应用于当前以及之前的输入。此外，他们还通过梯度下降和反向传播时间调整权重，我们将在下面的部分讨论。还要注意，尽管前馈神经网络将一个输入映射到一个输出，但RNN可以映射一对多，多对多(翻译)和多对一(分类语音)。

4. LSTM、GRU的结构

4.1 LSTM

  上面介绍的RNN模型，存在“长期依赖”的问题。模型在预测“大海的颜色是”下一个单词时，很容易判断为“蓝色”，因为这里相关信息与待预测词的位置相差不大，模型不需要记忆这个短句子之前更长的上下文信息。但当模型预测“十年前，北京的天空很蓝，但随着大量工厂的开设，废气排放监控不力，空气污染开始变得越来越严重，渐渐地，这里的天空变成了”下一个单词时，依靠“短期依赖”就不能很好的解决这类问题，因为仅仅根据“这里的天空变成了”这一小段，后一个单词可以是“蓝色”，也可以是“灰色”。上节描述的简单RNN结构可能无法学习到这种“长期依赖”的信息，LSTM可以很好的解决这类问题。

  与简单RNN结构中单一tanh循环体不同的是，LSTM使用三个“门”结构来控制不同时刻的状态和输出。所谓的“门”结构就是使用了sigmoid激活函数的全连接神经网络和一个按位做乘法的操作，sigmoid激活函数会输出一个0~1之间的数值，这个数值描述的是当前有多少信息能通过“门”，0表示任何信息都无法通过，1表示全部信息都可以通过。其中，“遗忘门”和“输入门”是LSTM单元结构的核心。下面我们来详细分析下三种“门”结构。
  遗忘门，用来让RNN“忘记”之前没有用的信息。比如“十年前，北京的天空是蓝色的”，但当看到“空气污染开始变得越来越严重”后，RNN应该忘记“北京的天空是蓝色的”这个信息。遗忘门会根据当前时刻节点的输入Xt、上一时刻节点的状态C(t-1)和上一时刻节点的输出h(t-1)来决定哪些信息将被遗忘。

  输入门，用来让RNN决定当前输入数据中哪些信息将被留下来。在RNN使用遗忘门“忘记”部分之前的信息后，还需要从当前的输入补充最新的记忆。输入门会根据当前时刻节点的输入Xt、上一时刻节点的状态C(t-1)和上一时刻节点的输出h(t-1)来决定哪些信息将进入当前时刻节点的状态Ct，比如看到“空气污染开始变得越来越严重”后，模型需要记忆这个最新的信息。

  输出门，LSTM在得到最新节点状态Ct后，结合上一时刻节点的输出h(t-1)和当前时刻节点的输入Xt来决定当前时刻节点的输出。比如当前时刻节点状态为被污染，那么“天空的颜色”后面的单词应该是“灰色”。

  在TensorFlow中可以使用lstm = rnn_cell.BasicLSTMCell(lstm_hidden_size)来声明一个LSTM结构。

4.2 LSTM李宏毅课程详解

4.2.1 简化版本的LSTM详解

  LSTM：long short-term memory，这里指的是long来形容short-term（这一点要注意）。

  LSTM是由三个门（输入门、输出门、遗忘门）、四大输入信号、一个输出信号构成的。其中每个门的输出是一个概率值，介于0~1之间，表示的是对信号的选择控制能力。

  每个门的输出是一个概率值，介于0~1之间，表示的是对相乘信号的选择控制能力。

  为了更好的理解，用举例的方式来讲解，其中x（输入数据）是由三个维度($x_1,x_2,x_3$)构成的，g和h均为sigmoid函数，为了简单起见，将所有的权重初始化为如图中的结果：

  当输入数据为第一组数据即[3, 1, 0]的时候，LSTM的值即为下图，计算结果为下下图：

  其中memory cell是对原有的值进行累加。
memory cell new value = 遗忘门的输出乘以memory cell old value + 输入门的输出乘以输入。这里假设g和h均为sigmoid函数。

  当输入数据为第二组数据即[4, 1, 0]的时候，LSTM的值即为下图，计算结果为下下图：


  当输入数据为第三组数据即[2, 0, 0]的时候，LSTM的值即为下图，计算结果为下下图：


  当输入数据为最后一组数据即[3, -1, 0]的时候，LSTM的值即为下图，计算结果为下下图：

4.2.2 LSTM与MLP的关系

  将LSTM和MLP进行对比，LSTM本质上只是把简单的神经元替换成了LSTM单元。

  原本是单个输入，现在变成了4个输入。

4.2.3 完整LSTM的结构

  其中四个输入$z^f,z^i,z,z^o$都是由$x^t$乘以一个矩阵得到的。

  把多个LSTM单元当作是LSTM单元的向量来看。

  把memory cell的值$c^t$、memory cell经过函数变换后的值$h(c^t)$、以及输入$x^{t+1}$。其中前两个均为上个LSTM单元的输出，所以输入为下一个时刻的结果。把三者拉成一个向量作为输入。

4.3 LSTM、GRU优缺点

  LSTM是一种特殊的RNN类型，一般的RNN结构如下图所示，是一种将以往学习的结果应用到当前学习的模型，但是这种一般的RNN存在着许多的弊端。举个例子，如果我们要预测“the clouds are in the sky”的最后一个单词，因为只在这一个句子的语境中进行预测，那么将很容易地预测出是这个单词是sky。在这样的场景中，相关的信息和预测的词位置之间的间隔是非常小的，RNN 可以学会使用先前的信息。


  标准的RNN结构中只有一个神经元，一个tanh层进行重复的学习，这样会存在一些弊端。例如，在比较长的环境中，例如在“I grew up in France… I speak fluent French”中去预测最后的French，那么模型会推荐一种语言的名字，但是预测具体是哪一种语言时就需要用到很远以前的Franch，这就说明在长环境中相关的信息和预测的词之间的间隔可以是非常长的。在理论上，RNN 绝对可以处理这样的长环境问题。人们可以仔细挑选参数来解决这类问题中的最初级形式，但在实践中，RNN 并不能够成功学习到这些知识。然而，LSTM模型就可以解决这一问题。

  如图所示，标准LSTM模型是一种特殊的RNN类型，在每一个重复的模块中有四个特殊的结构，以一种特殊的方式进行交互。在图中，每一条黑线传输着一整个向量，粉色的圈代表一种pointwise 操作(将定义域上的每一点的函数值分别进行运算)，诸如向量的和，而黄色的矩阵就是学习到的神经网络层。 LSTM模型的核心思想是“细胞状态”。“细胞状态”类似于传送带。直接在整个链上运行，只有一些少量的线性交互。信息在上面流传保持不变会很容易。

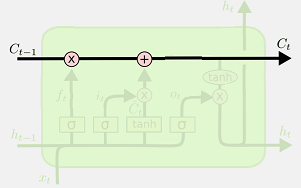
  LSTM 有通过精心设计的称作为“门”的结构来去除或者增加信息到细胞状态的能力。门是一种让信息选择式通过的方法。他们包含一个 sigmoid 神经网络层和一个 pointwise 乘法操作。 Sigmoid 层输出 0 到 1 之间的数值，描述每个部分有多少量可以通过。0 代表“不许任何量通过”，1 就指“允许任意量通过”。LSTM 拥有三个门，来保护和控制细胞状态。
  在LSTM模型中，第一步是决定我们从“细胞”中丢弃什么信息，这个操作由一个忘记门层来完成。该层读取当前输入x和前神经元信息h，由ft来决定丢弃的信息。输出结果1表示“完全保留”，0 表示“完全舍弃”。
  第二步是确定细胞状态所存放的新信息，这一步由两层组成。sigmoid层作为“输入门层”，决定我们将要更新的值i；tanh层来创建一个新的候选值向量~Ct加入到状态中。在语言模型的例子中，我们希望增加新的主语到细胞状态中，来替代旧的需要忘记的主语。
  第三步就是更新旧细胞的状态，将Ct-1更新为Ct。我们把旧状态与 ft相乘，丢弃掉我们确定需要丢弃的信息。接着加上 it * ~Ct。这就是新的候选值，根据我们决定更新每个状态的程度进行变化。在语言模型的例子中，这就是我们实际根据前面确定的目标，丢弃旧代词的信息并添加新的信息的地方。
  最后一步就是确定输出了，这个输出将会基于我们的细胞状态，但是也是一个过滤后的版本。首先，我们运行一个 sigmoid 层来确定细胞状态的哪个部分将输出出去。接着，我们把细胞状态通过 tanh 进行处理（得到一个在 -1 到 1 之间的值）并将它和 sigmoid 门的输出相乘，最终我们仅仅会输出我们确定输出的那部分。在语言模型的例子中，因为语境中有一个代词，可能需要输出与之相关的信息。例如，输出判断是一个动词，那么我们需要根据代词是单数还是负数，进行动词的词形变化。

4.4 GRU（ Gated Recurrent Unit，LSTM变体）

  GRU作为LSTM的一种变体，将忘记门和输入门合成了一个单一的更新门。同样还混合了细胞状态和隐藏状态，加诸其他一些改动。最终的模型比标准的 LSTM 模型要简单，也是非常流行的变体。

5. 针对梯度消失（LSTM等其他门控RNN）

5.1 梯度爆炸（梯度截断）的解决方案

  LSTM只能避免RNN的梯度消失（gradient vanishing），但是不能对抗梯度爆炸问题（Exploding Gradient）。梯度膨胀(gradient explosion)不是个严重的问题，一般靠裁剪后的优化算法即可解决，比如gradient clipping（如果梯度的范数大于某个给定值，将梯度同比收缩）。

梯度剪裁的方法一般有两种：

1. 一种是当梯度的某个维度绝对值大于某个上限的时候，就剪裁为上限。
2. 另一种是梯度的L2范数大于上限后，让梯度除以范数，避免过大。

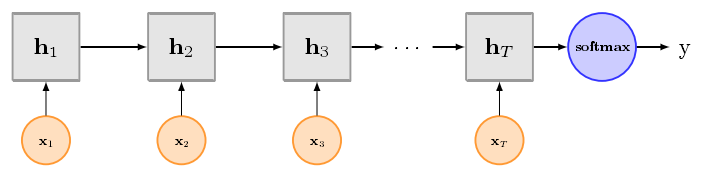
6. Text-RNN的原理

  TextCNN擅长捕获更短的序列信息，但是TextRNN擅长捕获更长的序列信息。具体到文本分类任务中，BiLSTM从某种意义上可以理解为可以捕获变长且双向的N-Gram信息。

7. 其他学习链接

  https://stanford.edu/~shervine/teaching/cs-230/cheatsheet-recurrent-neural-networks