熵、信息增益、信息增益率

一、熵

（1）原理

初中物理我们对“熵”这个东西懵懵懂懂，印象中仿佛对物体内部的热效应有关，时隔这么多年在机器学习、深度学习领域的学习中又看见了它的踪影，不免有点让人有点熟悉又陌生的感觉。“熵”这个东西看不见又摸不着，到底什么是“熵”？

“熵”是用来干什么的？“熵”是一个系统里面的混乱程度的度量、标尺。系统混乱程度越低，系统的熵值越小，反之越大。

我们先从物理学的角度出发，假设相同条件下有一桶冰水和一桶热水，哪一个的熵值会大呢？

冰水中的分子热运动速度较慢，内部的分子排布比较有规律。热水内部温度较高，因此分子热运动也比较剧烈，分子间的排布比较的松散。因此冰水的系统中的熵较低，热水中的熵较大。

• 信息理论：

1、从信息的完整性上进行的描述:

当系统的有序状态一致时，数据越集中的地方熵值越小，数据越分散的地方熵值越大。

2、从信息的有序性上进行的描述:

当数据量一致时，系统越有序，熵值越低；系统越混乱或者分散，熵值越高。

"信息熵" (information entropy)是度量样本集合纯度最常用的一种指标。

假定当前样本集合 D 中第 k 类样本所占的比例为 p_k​​ (k = 1, 2,. . . , |y|) ，，D为样本的所有数量，为第k类样本的数量。则 D的信息熵定义为(（log是以2为底，lg是以10为底）:

 

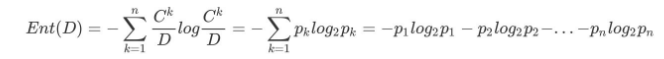
其中：Ent(D) 的值越小，则 D 的纯度越高.

（2）案例

假设一个月之后的某一天的天气可能有一下4种情况：晴天、多云、阴天、下雨。概率分别为{1/2, 1/4, 1/8, 1/8}。

那么在这条信息中信息熵计算如下：

 

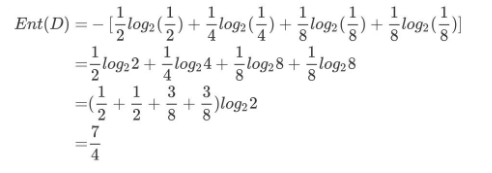
二、信息增益

（1）概念

信息增益：以某特征划分数据集前后的熵的差值。熵可以表示样本集合的不确定性，熵越大，样本的不确定性就越大。因此可以使用划分前后集合熵的差值来衡量使用当前特征对于样本集合D划分效果的好坏。

信息增益 = entroy(前) - entroy(后)

信息增益的计算方法如下图（摘抄自西瓜书75页），

（2）案例

如下表，第一列为学员号，第二列为学员性别，第三列为学习成绩提高程度，最后一列学员是否流失。

我们要解决一个问题：性别和学习成绩提高程度两个特征，哪个对学员流失影响更大？

    

其中Positive为正样本（已流失），Negative为负样本（未流失），下面的数值为不同划分下对应的人数。

可得到三个熵：

1、计算类别信息熵

      整体熵：

                   

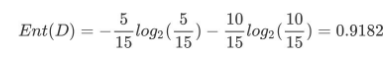
2、计算性别属性的信息熵(a="性别")

3、计算性别的信息增益(a="性别")

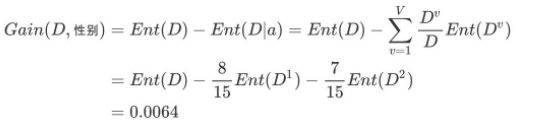
4、计算进步程度度属性的信息熵(a="进步程度")

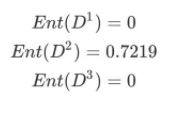
5、计算进步程度度的信息增益(a="进步程度")

进步程度的信息增益比性别的信息增益大，也就是说，进步程度对学员流失的影响比性别大。在做特征选择或者数据分析的时候，我们应该重点考察进步程度这个指标。

 

三、信息增益率

（1）概念

在上面的介绍中，我们有意忽略了"编号"这一列.若把"编号"也作为一个候选划分属性，则根据信息增益公式可计算出它的信息增益为 0.9182，远大于其他候选划分属性。但是很明显这么分类,最后出现的结果不具有泛化效果.无法对新样本进行有效预测。

信息增益准则对可取值数目较多的属性有所偏好，为减少这种偏好可能带来的不利影响，著名的 C4.5 决策树算法 [Quinlan， 1993J 不直接使用信息增益，而是使用"增益率" (gain ratio) 来选择最优划分属性。

（2）案例

接着上面的案例，我们来计算性别的信息增益率和进步程度的信息增益率。

1、计算属性分裂信息度量

用分裂信息度量来考虑某种属性进行分裂时分支的数量信息和尺寸信息，我们把这些信息称为属性的内在信息（instrisic information）。信息增益率用信息增益/内在信息，会导致属性的重要性随着内在信息的增大而减小（也就是说，如果这个属性本身不确定性就很大，那我就越不倾向于选取它），这样算是对单纯用信息增益有所补偿。

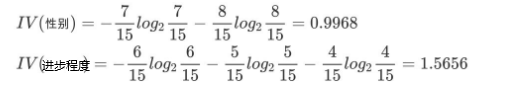
2、计算信息增益率

进步程度的信息增益率更高一些，所以在构建决策树的时候，优先选择通过这种方式，在选取节点的过程中，我们可以降低取值较多的属性的选取偏好。