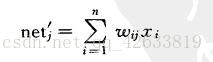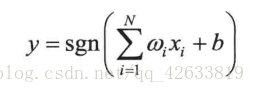神经网络学习（1）————单层感知器以及python实现_单层感知网络算法

一、感知器模型

单层感知器是感知器中最简单的一种，有单个神经元组成的单层感知器只能用于解决线性可分的二分性问题。在空间中如果输入的数据是可分的，感知器相当于将输入的数据在空间中分为两类，已经证明，如果线性可分则算法一定收敛。单层感知器是指只有一层处理单元的感知器，其中输入层没有处理数据的能力，输入层有n个神经元结点，每个结点接受一个输入信号xi，输入层与输出层之前有权重w，将每个结点组成的输入矩阵和权值矩阵相乘，得到一个数，将这个数作为净输入传递给神经元细胞，再将净输入代入神经元细胞的激活函数中，并且在神经元中还有一个外部偏置b，激活函数在这里一般采用符号函数，然后输出一个数。

数学表示：输入矩阵：X=(X1,X2,X3,X4,X5,……Xn)；

          权值矩阵：W=(W1j,W2j,W3j,W4j,……Wnj)；

          输出矩阵：Y=(Y1,Y2,Y3,……Ym)；

下图是单层感知器模型：

  

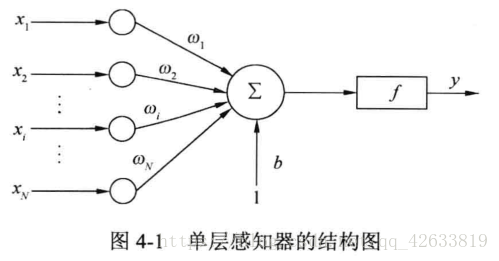
在输出层的每一个节点上接受来自输入层的加权和作为输出层的净输入：

输出的值由激活函数决定：

 

二、单层感知器的学习算法

其中，L1为一类，L2为另一类；为学习率，它的值决定了误差对权值的影响大小，值不应该过大，以便为输入向量提供一个比较稳定的权值估计；值也不能过小，

收敛条件：当权值向量已经能正确实现分类时，算法就收敛了。计算时收敛条件通常是：1）理想值和计算得出的值得差小于一个提前设定的值；2）权值两次变化的值小于一个提前设定的值；3）设定一个最大迭代数M。

 

三、局限性和解决途径

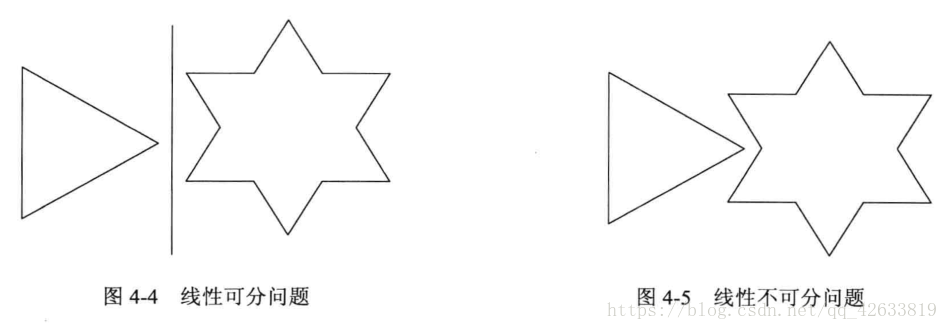
单层感知器可以实现线性可分的问题，一旦出现非线性问题则无效。

解决这一局限的有效办法是，在输入层和输出层之间引入隐层，将单计算层感知器变成多计算层感知器。

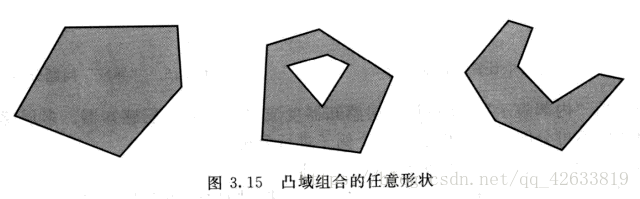
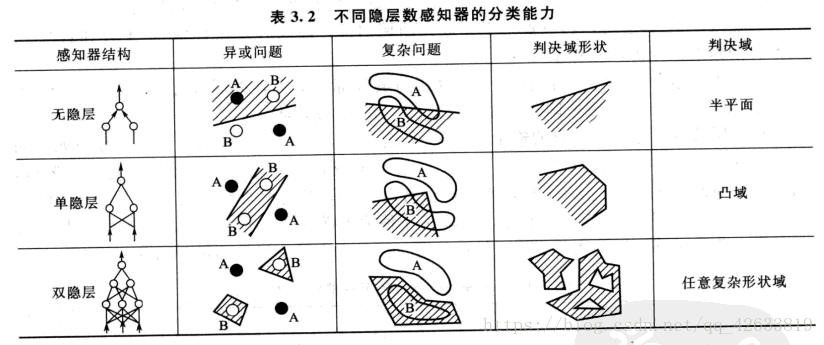
    当单隐层感知器具有多个结点时，结点数量增加可以多边形凸域的边数，从而在输入空间构建出任意形状的凸域，如果在此基础上再增加一层，成为第二个隐层，则该层的每个节点确定一个凸域，各种凸域组合成为任意形状域。如图：

提高分类能力的另一个途径就是采用非线性连续函数作为神经元结点的激活函数，也叫转移函数。

多层感知器从理论上可解决线性不可分问题，但是从前面的学习规则可知，权值的调整取决于感知器期望输出与实际输出之差，但是对于各隐层结点来说，不存在期望输出，因此该学习规则对隐层权值不适用。

多层感知器能提高网络的分类能力，但是没有提出关于权值调整的有效算法。后来有学者对具有非线性连续激活函数的多层感知器进行分析，得出了BP网络，实现了多层感知器的设想。

 

单层感知器包括输入结点、输出节点、权向量、偏执因子、激活函数、学习率等。

 

 

 

训练的目的是找到合适的权值和偏置因子。

最后是python实现：

# -*- coding: utf-8 -*-
"""
Created on Thu Sep 27 19:33:12 2018
@author: Heisenberg
"""
 
import numpy as np
import matplotlib.pyplot as mpl
 
#输入数据矩阵
X=np.array([[1,2,3],[1,4,3],[1,5,8]])#为简单起见，第一项为偏置向量，设置为1；
#目标函数
Y=np.array([1,1,-1])
#权值初始化
W=(np.random.random(3)-0.5)*2#第一项为偏置值,权值矩阵取值范围为[-1,1].
print(W)
#学习率
lr =0.1
#迭代次数
n=0
#神经网络输出
o=0
#权值更新
def update():
   global X,Y,W,lr,n
   n=n+1
   O=np.sign(np.dot(X,W)) #实际输出
   W1=lr*((Y-O).dot(X))#a.dot(b)和dot(a,b)效果一样，这里Y根据属于哪一类值为1或者-1，
   W = W + W1
   
for i in range(100):
    update()#更新权值
    print(W)
    print(n)
    O=np.sign(np.dot(X,W)) #实际输出
    if(O==Y).all():
        print("完成")
        print("迭代次数：",n)
        break
    
#实例部分
#正样本
x1=[2,4]
y1=[3,3]
#负样本
x2=[5]
y2=[8]
#计算分界线斜率以及截距
k=-W[1]/W[2]
d=-W[0]/W[2]
print("斜率=",k)
print("截距=",d)
#x轴的刻度划分一个8个刻度
xdata=np.linspace(0,8)
 
mpl.figure()#调用函数创建一个绘图对象，并且使他成为当前的绘图对象
mpl.plot(xdata,xdata*k+d,'r')# r代表是红色
mpl.plot(x1,y1,'bo')  #x1,y1的俩个点用蓝色圆圈标记
mpl.plot(x2,y2,'yo')  #黄色标记
mpl.show()

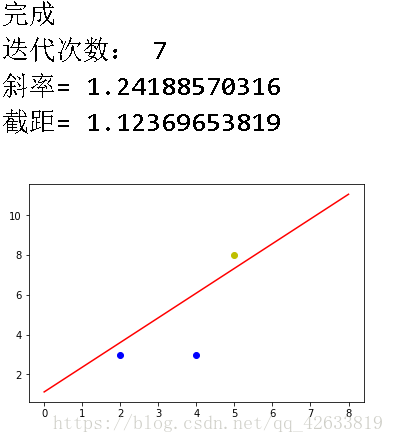
计算结果：